More than 5 years have passed since last update.

機械学習で精度が出ない時にやることまとめ

Last updated at 2019-05-29Posted at 2017-01-10

機械学習を1ヵ月で実践レベルにする 14日目

この記事は「機械学習を機械学習を1ヵ月で実践レベルにする」シリーズの14日目の記事です。

第一日目の記事はこちら
機械学習を1ヵ月で実践レベルにする #1 (とっかかり編)

その他の記事は、本記事の末尾にインデックスをつけています。
それでは本題へ。

精度がでないとき、次に何をやるか

ある予測モデル(分類でも可)で大きな誤差を生んでいたら次になにをすればよいか

よくやりがちなのが「精度が出ないのはトレーニングデータが足りないからだ！」などといって、いきなりデータ集めに走ってしまうことだそうです。綺麗事をいわずに泥臭くデータ集めができること自体は立派な場合もありますが、無駄な努力に終わることも多いです。それでも「やってみなければわからない」と思うかもしれませんが、やる前からわかることもあります。

精度向上対策の候補

精度向上のための対策の候補にはどんなものがあるでしょうか。

トレーニングデータをもっと集める
特徴量 $n$ を減らす
特徴量 $n$ を増やす
高次の特徴を追加する($x_1^2, x_2^2,x_1x_2,\ldots)$
正則化の係数 $\lambda$ を小さくする
正則化の係数 $\lambda$ を大きくする

※ 学習率 $\alpha$ に問題があるケースもありますが、これはモデルの問題ではなく収束速度の問題で、どちらかというと解析的な問題であり、大体の場合、最小化ライブラリが解決してくれるのでここでは省略します。

これらはどれも対策として正しいのですが、どれが正しいかはすぐにはわかりません。ここで直感で「xx をやってみよう」というのは絶対にダメだと、Ng 教授は仰っておりました。これは無駄な時間の使い方とのことです。

そのためには診断をすべきであると。診断ももちろん時間がかかるのですが、それは良い時間の使い方とのことでした。

診断

診断をするまえに、まずそのモデルが正しく予測できているかどうかを判断するためのテスト手法が必要になります。

テスト

テストというのは、未知の値を予測するのではなく、すでに結果がわかっているデータに対してモデルを適用してみて、その予測値と実際の値の誤差の割合から、そのモデルの優秀さ、精度などを評価することをいいます。

すでに結果がわかっているデータというのは他でもない、トレーニングデータのセットです。いままではトレーニングデータをすべて使ってモデルを構築していましたが、まず、このトレーニングデータのうち30% 程度をテストデータとしてよけておきます。

ただし、ランダムにわける必要があります。すでにランダムなデータセットであれば上から70% をトレーニングデータに使い、下30% をテストデータに使うということでよいのですが、なにかしらの条件でソートされているデータの場合には、予めシャッフルしてから7:3 にわけるとよいです。

そして、70% にしたトレーニングデータ(以下、これをトレーニングデータと呼ぶ)でコスト関数を作ります。

線形回帰の場合

トレーニングデータでコスト関数を作る
そのコストを最小にするための $\theta$ を求める
その $\theta$ をテストデータに適用してコスト関数に代入して誤差を求める

$$ J_{ test }(\theta) = \frac{ 1 }{ 2m_{ test } }\sum_{ i = 1 }^{ m_{ test } } (h_\theta(x_{ test }^{ (i) }) - y_{ test }^{ (i) })^2 $$

これが小さければ予測精度は優秀で、これが大きいとなにかがおかしいということになります。

ロジスティック回帰の場合

ロジスティック回帰の場合も手順はほとんど同じですが、予め誤差関数を定義しておいてそれで評価します。

誤差関数

err(h_\theta(x), y) = \left\{
\begin{array}{ll}
1 & (h_\theta(x) \geq 0.5, y = 0 \quad or \quad h_\theta(x) \lt 0.5, y = 1) \\
0 & (otherwise)
\end{array}
\right.

式で見ると難しく感じるかもしれませんがよくみると簡単です。要は、仮説関数が0.5以上で $ y=1 $を予測するのですが、実際には $y=0$だった場合に、エラー ($ = 1 $)とし、同様に、仮説関数が0.5未満で $ y=0 $を予測しているのに実際には $y=1$だったときにもエラー ($ = 1 $)とし、それ以外の場合には非エラー ($ = 0 $)としているだけです。

トレーニングデータでコスト関数を作る
そのコストを最小にするための $\theta$ を求める
その $\theta$ をテストデータに適用して誤差関数に代入してご判別の割合を求める

$$ Test_{ error } = \frac{ 1 }{ m_{ test } }\sum_{ i = 1 }^{ m_{ test } }err(h_\theta(x_{ test }^{ (i) }), y_{ test }^{ (i) }) $$

まずここまでで、作ったモデルの精度を評価する手段を手に入れました。

モデル選択の問題

次に、特徴量がどのくらいであれば最適かどうかを診断するところから、診断の手順をみていきたいと思います。例えば、以下のように、1次から10次までの多項式でモデルを検討したとします。

\begin{align}
&d = 1, \quad h_\theta(x) = \theta_0 + \theta_1x \\
&d = 2, \quad h_\theta(x) = \theta_0 + \theta_1x + \theta_2x^2 \\
&\vdots \\
&d = 10, \quad h_\theta(x) = \theta_0 + \theta_1x + \ldots + \theta_{ 10 }x^{ 10 }
\end{align}

この場合、それぞれでそのコストを最小にする $ \Theta $ を計算します。いま、その次数に対応する $ \Theta $ を上付きの添字をつけて $ \Theta^{(2)} $ などと表すことにします。これは $d=2$ のときの例です。

そうしてどの $\Theta$ がコストを最小にするかをテストデータを使って調べてみたところ、 $ d = 4 $ のとき、つまり $ J_{ test }(\Theta^{ (4) }) $ が最小だったとします。これで次数は4にするのがよいと結論づけてしまいそうですが、これには少し問題があります。

最後の次数を最適化するところで、テストデータに対して最適な次数を決定していますので、これが未知のデータに対してうまくフィットするかは疑問です。すでにテストデータにフィットするものを選んでしまっているので。

交差検証

そこで交差検証というものを行います。さきほどは初期に与えられたデータセットのうち、70% をトレーニングデータ、３０％をテストデータとしましたが、今度は、60%をトレーニングデータ、20%を交差検証(以下、cv)用のデータ、20%をテストデータとします。

このように分けたうえで、先程のような、モデル選択の問題においては

トレーニングデータで $\Theta $ を決定
cv データでそれらの $\Theta $ を用いて、コスト(or 誤差)が最小になるモデルを選択
テストデータで、選択したモデル及び $\Theta $ を用いて精度を確認

という流れで行います。これで、フェアなテスト、及び診断が可能になります。

High bias / High variance 診断

最後にその誤差が何に起因するものなのかを考えてみます。先程見た、多項式の次数で考えてみましょう。多項式の次数というのは特徴量 $n$ の多さともいえます。以前みたように、次数が低いとアンダーフィットしてしまい、次数が高いともオーバーフィットしてしまいます。

左のように次数が低いとアンダーフィットしています。これをHigh bias の状態といいます。また、右のように次数が高すぎるとオーバーフィットしています。これをHigh variance の状態といいます。

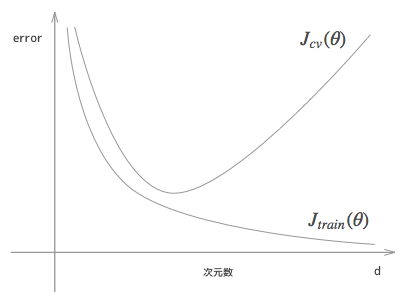
さてここで、トレーニングデータにおけるコスト関数と、交差検証(またはテスト)データにおけるコスト関数の、次数による変化をみてみましょう。

結論からいうとこのような形になります。なぜこうなるか考えて行きます。

次数が低い場合、このグラフでいう左側のほうですが、この場合は、バラバラにならんだデータにうまくフィットできず、トレーニングデータでも高い誤差があり、当然cvデータでも高い誤差があるという、アンダーフィットの状態になります。

そして次数を高くしていくと、トレーニングデータとcvデータはともに誤差が下がり、よりよいモデルに近づいてきているように見えます。

しかしさらに高い次数にすると、トレーニングデータにはどんどんフィットしていきますが、逆にトレーニングデータにだけ過剰にフィットしている状態となり、cv データのほうは段々とまた誤差が大きくなっていきます。これがオーバーフィッティングしている状態です。

これを見ると、アンダーフィッティングしているときには、特徴量 $n$ を増やす方向で検討するのがよく、また、オーバーフィッティングしているときには特徴量 $n$ を減らす方向で検討するのがよいというのがわかります。(実際には特徴量を減らすよりは、後述の正則化を大きくするほうが良いと、Ng 先生は言っています。経験上)

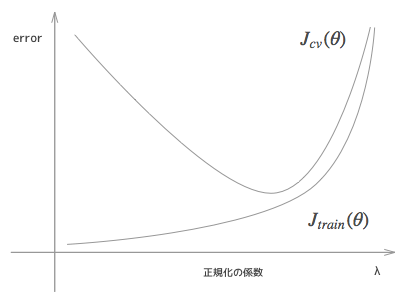
いまは次数についてどう考えてどう決定していくかを見ていましたが、他のパラメータについても同様です。例えば正則化の係数である $ \lambda $ についてもグラフを書いてみますと以下のようになります。

$ \lambda $ はオーバーフィッティングを調整するための係数でした。$ \lambda $ が0ということは正則化をまったくしないのと同じことですから、オーバーフィッティングに対する調整がないのと同等ですので、トレーニングデータにだけフィットしすぎていて、cvデータでは誤差が大きいという、上のグラフでいう左のほうの状態になります。

また、$ \lambda $ を過剰に大きくするということは、高次の項のペナルティを大きく課すということですから、結果的に、高次の項については無視するのと同等になり、低次の関数でモデルを作ることと同等になりますから、アンダーフィッティングの状態と同じになり、上のグラフでいう右のほうの状態になります。

トレーニングデータ数について

このようにして調整できるパラメータに対してのそのコスト関数の変化をグラフにしたものを学習曲線といいます。これを見ていくことで、今後の方針を立てることができるようになります。最後に、トレーニングデータ数を横軸にとった学習曲線を見てみます。

これはHigh bias のときの典型的な学習曲線です。アンダーフィッティングのときは、データ数が増えてもグラフがそんなに変化する自由度がありませんから、誤差があまり縮まりません。このときは結果的にデータ数を増やしてもある一定以上には、トレーニングデータ、cv データともに改善がみられません。こういった状態で誤差があるときに、データをもっと集めても徒労に終わってしまうのです。

繰り返しになりますが、トレーニングデータにおける誤差と、cv データにおける誤差の差が小さく、かつ誤差そのものは大きいという状態のときは、アンダーフィッティングしているときなので注意してください。

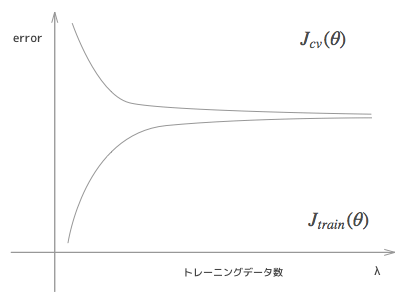
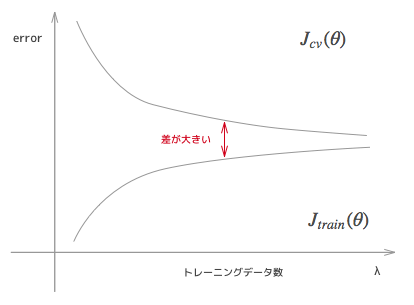
こちらはHigh variance のときの学習曲線です。この場合は、トレーニングデータにおける誤差とcv における誤差の差が大きいのが特徴です。この状態であればトレーニングデータを増やす対策も一定の効果をあげるでしょう。

まとめ

まずその誤差が何に起因するものなのかを診断する。いろいろなパラメタで学習曲線をひくというのは、手間がかかりますが、徒労には終わりません。必ずなにかを得られる時間の使い方なので、Ng 教授も強く推薦している方法です。そして、High Variance なのか、High Bias なのかを見てみます。。それに応じて、次の手を打っていくという形になります。

	High variance	High bias
トレーニングデータをもっと集める	o	x
特徴量 $n$ を減らす	o	x
特徴量 $n$ を増やす	x	o
高次の特徴を追加する($x_1^2, x_2^2,x_1x_2,\ldots)$	x	o
正則化の係数 $\lambda$ を小さくする	x	o
正則化の係数 $\lambda$ を大きくする	o	x

※

High variance = オーバーフィッティング
High bias = アンダーフィッティング

以上です。

過去記事一覧

545

514

You get articles that match your needs
You can efficiently read back useful information
You can use dark theme

What you can do with signing up