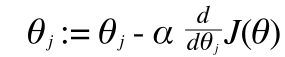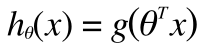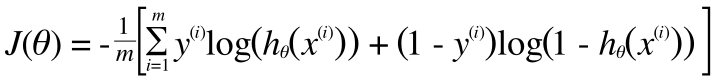8日目
クリスマスも返上してやっていた Coursera でStanford が提供しているMachine Learning ですが、おかげさまで、WEEK 7まで修了しました。
このWEEK 1〜7 でどこまでやったか振り返ってみました。多変量の線形回帰、ロジスティック回帰、それらに正規化をほどこす理由とその実践、ニューラルネットワーク、サポートベクターマシン(SVM)、これらのアルゴリズムの使い分けから、パラメタの最適化の仕方、それらのOctave での実装から改善までの手順、最後に、実際にスパムフィルターを作ってみて実戦と、かなり充実しています。
そして厳しいクイズとテストのおかげで、理解度としてもほぼ100% です。Ng 先生がいうには、大事なことなので2回目ですが、すでにシリコンバレーで活躍している多くの機械学習エンジニアより、おそらく理解しているだろうとのこと。嬉しいですね。WEEK 7 までで教師あり学習はおしまいで、次回からは教師なし学習に入るようです。この勢いでWEEK 11 まで一気に終わらせたいと思います。
過去記事一覧
- 1日目 とっかかり編
- 2日目 オンライン講座
- 3日目 Octave チュートリアル
- 4日目 機械学習の第一歩、線形回帰から
- 5日目 線形回帰をOctave で実装する
- 6日目 Octave によるVectorial implementation
- 7日目 ロジスティック回帰 (分類問題) その1
- 8日目 ロジスティック回帰 (分類問題) その2
- 9日目 オーバーフィッティング
- 10日目 正規化
- 11日目 ニューラルネットワーク #1
- 12日目 ニューラルネットワーク #2
- 13日目 機械学習に必要な最急降下法の実装に必要な知識まとめ
- 14日目 機械学習で精度が出ない時にやることまとめ
- 最終日 機械学習をゼロから1ヵ月間勉強し続けた結果
ロジスティック回帰の続き
さて、それでは前回の続きです。
前回はロジスティック回帰における仮説関数とコスト関数の定義まで紹介しましたので、今回はそのコストを最小化するための、最急降下法の実践にうつって行きたいと思います。
復習ですが、線形回帰の場合のコストは下記で表すことができました。
$$
\operatorname { cost } \left( h _ { \theta } ( x ) , y \right) = \frac { 1 } { 2 } \left( h _ { \theta } ( x ) - y \right) ^ { 2 }
$$
しかし、ロジスティック回帰では仮説関数が
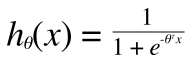
このように線形ではないために凸関数にならず(この証明は本題ではないので割愛)、最急降下法で極小をもとめてもそれが最小とは限らずうまくいきません。そこで、Cost をあらたに定義しなおします。
まず、 y の値は 0 または 1 しかとりません。それから h(x) は 0 ≤ h(x) ≤ 1 の値しかとりません。これらを総合して、今後の計算がしやすいように、あらたなCost を下記のように定義します。
$$
\operatorname { cost } \left( h _ { \theta } ( x ) , y \right) = - \log \left( h _ { \theta } ( x ) \right) \text { if } y = 1
$$
$$
\operatorname { cost } \left( h _ { \theta } ( x ) , y \right) = - \log \left( 1 - h _ { \theta } ( x ) \right) \text { if } y = 0
$$
この関数の特徴として
y = 1 のときは、 h(x) = 1 でCost がちゃんと0になり
y = 0 のときは、 h(x) = 0 でCost がちゃんと0になります。
そして、
y = 1 のときは、 h(x) = 0 でCost が無限大になり
y = 0 のときは、 h(x) = 1 でCost が無限大になります。
直感と一致しますよね。
グラフでも書いておきます。
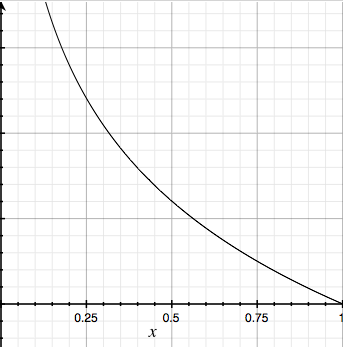
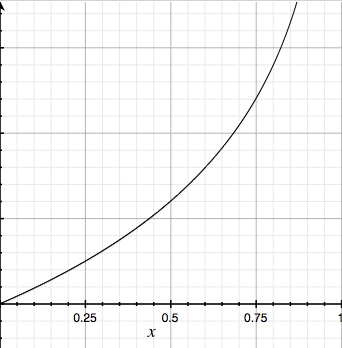
(左がy = 1 のとき、右がy = 0 のとき)
これを場合わけせずに書くとこのように表せます。
(第二項の符号がプラスになってしまっていたのをマイナスに修正しました。2016/12/28)
$$
\operatorname { cost } \left( h _ { \theta } ( x ) , y \right) = - y \log \left( h _ { \theta } ( x ) \right) - ( 1 - y ) \log \left( 1 - h _ { \theta } ( x ) \right)
$$ (y に 0 や 1 を代入して頂けるとすぐにわかるかと思います)
以上より、ロジスティック回帰のコスト関数J(θ) は次のように書き表せます。
$$
J ( \theta ) = - \frac { 1 } { m } \sum _ { i = 1 } ^ { m } \left[ y ^ { ( i ) } \log \left( h _ { \theta } \left( x ^ { ( i ) } \right) \right) + \left( 1 - y ^ { ( i ) } \right) \log \left( 1 - h _ { \theta } \left( x ^ { ( i ) } \right) \right) \right]
$$ 式だけみると複雑そうにみえますが、ここまでの流れを追えば必然性を感じられることと思います。
最急降下法
さて、これでお得意の最急降下法を使う準備が整いました。最急降下法は#4 で紹介しています。最急降下法では、その傾き方向に歩いて行くわけですから、やはりここでも偏微分を使います。
こんな形ですね。(すみません。ラウンドディーが書けなかったで常微分のように見えますが、d のところは偏微分だと思ってください)
ちなみにθに添字のj がついているのは、θのj番目の要素ということで、実数(スカラー)です。あとに出てくる、添字なしのθはベクトルです。
そしてこの偏微分の項目を計算すると(過程は本題からはずれるので省略)
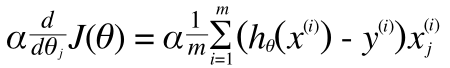
このようになり、線形回帰のときとおなじ形が得られます。
以上より、
Repeat {
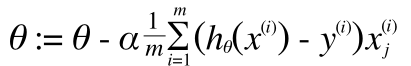
}
(ベクトル表現になっていることに注意してください)
これをOctave などで実装して繰り返して計算していくと、コストを最小にするθに収束していき、目的のθを得られることになります。
Octave での実装
まず、シグモイド関数を定義しておきます。
function g = sigmoid(z)
g = zeros(size(z));
g = 1 ./ (1 + e.^(-z))
end
これで、z は実数(スカラー)だけでなく、行列にも対応しています。行列の場合、全要素にsigmoid を適用した結果が返されます。
あとはいままで見てきたものをOctave で実装するだけです。
X はトレーニングデータセットで、m x n の行列です。
y はトレーニングデータセットの結果です。
m はトレーニングデータの数(要素数)で、n は特徴の数です。
theta は必然的に、n x 1 の行列(=n次ベクトル)です。
hx = sigmoid(X * theta);
ここでのtheta は初期値です。この後、最急降下法で最適なtheta に収束させるので次元さえあっていればなんでもいいのですが、慣習的にすべて0 のベクトルにすることが多いようです。つまり、要素がすべて0のn次ベクトルです。octave で表すならこんな感じでしょうか。
n = size(X, 2);
theta = zeros(n, 1);
J = -1 / m * sum(y.*log(hx) + (1 - y).*log(1 - hx));
grad = 1 / m * (X' * (hx - y));
Octave で勾配項だけを定義しているのは、コスト関数と勾配項を渡すと、最急降下法などを(最適化されたαで)自動で計算してくれるライブラリなどがあるため、こうしておくと使いやすいからです。もちろんこの grad を使って、自前でfor loop させてθ を収束されることもできます。
ロジスティック回帰流れまとめ
- θに依存する仮説関数を定義する(h(x))
- J(θ) を定義する(思い出す)
- これにトレーニングデータをぶち込む(sigmoid をかけつつ)
- トレーニングデータをぶちこむ準備としてsigmoid 関数を定義しておく
- 適当な初期θを用意する
- J(θ) の定義から導出されるgrad とトレーニングデータから、最急降下法を使って最適なθに収束させる
- 最適化されたθによる仮説関数 h(x) が得られる
- 未知のx を h(x) に入れることで、予測値を得ることができる。