はじめに
手書き数字画像(MNIST)の分類を、Google Colaboratory 環境の TensorFlow2 + Keras でやってみよう(+Pythonや深層学習の理解も深めよう)という内容です。前回 は、TensorFlow の 公式HPのチュートリアル からサンプルコードを持ってきて、実際に実行してみる、というところまでやりました。
- TensorFlow2 + Keras による画像分類に挑戦 シリーズ
なお、**MNIST(エムニスト)**は、「図解速習DEEP LEARNING(著:増田知彰)」によれば、次のような由来があるデータだそうです。ここでは直接関係ありませんが、生のデータは、http://yann.lecun.com/exdb/mnist/ から入手できます。
NIST(National Institute of Standards and Technology database)の1つに、米国の国勢調査局職員と高校生が手書きした数字を持つデータセットがありました。それを機械学習でより使いやすく改変(Modified)したものが、"M"NISTです。
今回は、前回に示したサンプルコードのなかの トレーニング用データ(x_train、y_train)、テスト用データ(x_test、y_test)について、その内容を詳しく見てみたり、matplotlib を使って可視化してみたりします。
それにあたり、まずは「多クラス分類問題」と「深層学習」について整理しておきます(トレーニング用データとテスト用データの位置づけを確認します)。
多クラス分類問題
手書き数字の認識は、多クラス分類問題というものに属します。多クラス分類問題とは、入力データに対して、そのカテゴリ(クラス)を予測するという問題です。カテゴリは、問題設定のなかで「犬」「猫」「鳥」のようにあらかじめ与えられており、入力データ(例えば画像)に対してそれが「犬」「猫」「鳥」のうち、どのカテゴリになるかを求める、といった問題になります。
多クラス分類問題に対して様々なアプローチが提案されていますが、ここでは深層学習(ディープラーニング)を使って解決していきます。
深層学習
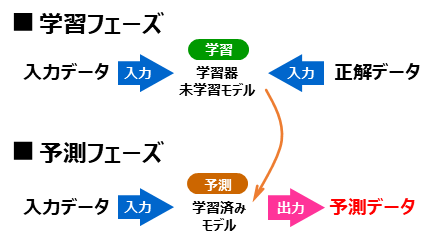
深層学習(ディープラーニング)は、教師付き機械学習という手法に属します。教師付き機械学習は、大きく「学習フェーズ」と「予測フェーズ(推論フェーズ、適用フェーズ)」という2段階から構成されます。
はじめに、学習フェーズでは、入力データと正解データ(=教師データ、正解データ、正解値、正解ラベル)をペアにしたものをモデルに大量に与えて、それらの関係を学習させます。これらの入力データと正解データのペア集合をトレーニング用データ(=学習用データ)と呼びます。そして、トレーニング用データを使って学習させたモデルを「学習済みモデル」といいます。
つづく予測フェーズでは、学習済みモデルに対して、未知の入力データを与えて出力の予測(Predict)を行ないます。多クラス問題であれば、カテゴリ(例えば「犬」など)が予測出力となります。
そして、「学習済みモデルにどの程度の性能があるか」を測るのが評価(Evaluate)というプロセスになります。評価では、まず、トレーニングに使ったものとは異なる入力データと正解データを用意して、このうち入力データだけを学習済みモデルに与えて、予測データを得ます。そして、この得られた予測データについて、正解データを使って答え合わせ、採点をして評価値とします。具体的な評価指標としては、前回出てきた正答率(accuracy)、損失関数値(loss)のほかに、適合率や再現率など必要に応じて様々なものが採用されます。
MNISTのトレーニング用データ、テスト用データ
次のコードで、MNISTデータをダウンロードして、各変数(x_train、y_train、x_test、y_test)に格納しています(プログラム全体は前回 を参照)。
mnist = tf.keras.datasets.mnist
(x_train, y_train), (x_test, y_test) = mnist.load_data()
ここで、*_train がトレーニング用(学習用)に割り当てられた入力&正解データ、*_test がテスト用(モデル評価用)に割り当てられた入力&正解データとなります。トレーニング用は 60,000件、テスト用は 10,000件 あります。
また、x_*** には入力データ(つまり手書き画像を表すデータ:28x28の256段階グレースケール)、y_*** には正解データ(「0」から「9」までのカテゴリ)が、配列的に格納されています。
まずは、実際に、それぞれが 60,000件、10,000件 のデータから構成されていることを len() で確認してみます。
# トレーニング用データ
print(len(x_train)) # 実行結果 -> 60000
print(len(y_train)) # 実行結果 -> 60000
# テスト用データ
print(len(x_test)) # 実行結果 -> 10000
print(len(y_test)) # 実行結果 -> 10000
次に、各データの**タイプ(型)**を確認してみます。
print(type(x_train)) # 実行結果 -> <class 'numpy.ndarray'>
print(type(y_train)) # 実行結果 -> <class 'numpy.ndarray'>
print(type(x_test)) # 実行結果 -> <class 'numpy.ndarray'>
print(type(y_test)) # 実行結果 -> <class 'numpy.ndarray'>
次に、y_train(=トレーニング用の正解データ)の内容を確認してみます。
print(y_train) # 実行結果 -> [5 0 4 ... 5 6 8]
0件目のデータの正解値は「5」、1件目のデータの正解値は「0」・・・、59,999件目のデータの正解値は「8」ということが分かりました。
次に、x_train(=トレーニング用の手書き画像を表すもの)の内容を確認してみます。全件を表示するととんでもないことになるので、先頭の x_train[0] のみを対象にします。
(x_train, y_train), (x_test, y_test) = mnist.load_data()
print(x_train[0].shape) # 実行結果 -> (28, 28)
print(x_train[0]) # 実行結果 -> 下記参照
numpy.ndarray のデータは、.shape で大きさが確認できます。 (28, 28)、ということは、x_train[0] が28行28列の2次元配列で構成されていることが分かります。また、print(x_train[0]) の出力は次のようになります。
薄眼で眺めていただくと、ややいびつな手書きの「5」という数字が浮かんできます。これは、y_train[0] に格納されている「5」と一致しますね。
各ピクセルデータは、0から255の範囲の値で構成されて、0が背景(白)で、255が最も濃い文字部(黒)になっていることが分かります。
60,000個の全てのデータについて、それを確認してみたいと思います。
import numpy as np
print(x_train.min()) # 最小値を抽出 # 実行結果 -> 0
print(x_train.max()) # 最大値を抽出 # 実行結果 -> 255
すべてのデータは0から255の範囲で構成されていることが確認できます。
ところで、60,000件のトレーニング用データのなかに、「0」から「9」までの各数字は何件ずつ存在するのでしょうか?基本的には、0から9までの10パターンがほぼ均等に存在していると思いますが、確認してみます。集計にpandasを利用します。
import pandas as pd
tmp = pd.DataFrame({'label':y_train})
tmp = tmp.groupby(by='label').size()
display(tmp)
print(f'総数={tmp.sum()}')
label
0 5923
1 6742
2 5958
3 6131
4 5842
5 5421
6 5918
7 6265
8 5851
9 5949
dtype: int64
総数=60000
「5」が少なくて「1」が多いといった多少のバラつきがあるようです。
なお、次のように pandas を使わなくても求めることができます。
import numpy as np
tmp = list([np.count_nonzero(y_train==p) for p in range(10)])
print(tmp) # 実行結果 -> [5923, 6742, 5958, 6131, 5842, 5421, 5918, 6265, 5851, 5949]
print(f'総数={sum(tmp)}') # 実行結果 -> 総数=60000
次回
- matplotlib を使って入力データをグラフィカルに表示するところまで進めたかったのですが、記事が長くなってしまったので、それは次回にしたいと思います。