はじめに
TensorFlow2 + Keras を利用した画像分類(Google Colaboratory 環境)についての勉強メモ(第8弾)です。題材は、ド定番である手書き数字画像(MNIST)の分類です。
- TensorFlow2 + Keras による画像分類に挑戦 シリーズ
前回は、TF公式HPの「初心者のための TensorFlow 2.0 入門」で取り上げられているニューラルネットワークモデルについて、それを構成する各層(Dense層、Dropout層、Flatten層)と活性化関数(ReLU関数、Softmax関数)の観点から、その概要を理解しました。
今回は、チュートリアルのプログラムの model.compile のところ(最適化アルゴリズムや損失関数の設定)について、理解していきたいと思います。
model.compile(optimizer='adam',
loss='sparse_categorical_crossentropy',
metrics=['accuracy'])
また、同じ構成のニューラルネットモデルであっても、学習に用いる最適化アルゴリズムの違いにより正解率(accuracy)や損失関数値(loss)、収束速度、計算時間が大きく変わることを実験により確認します。そこでは、次のようなグラフを作成していきます。
モデルのコンパイル model.compile(...) について
TF公式HPの「初心者のための TensorFlow 2.0 入門」のチュートリアルプログラムのでは、tf.keras.models.Sequential(...) によって、ニューラルネットの層構成を定義したあと、それをトレーニングする前に、compile(optimizer=..., loss=..., metrics=...) というプロセスをはさんでいます。
-
model.compile()のリファレンスはこちらを参照
このプロセスでは、ニューラルネットモデルのトレーニング(重みパラメータの最適化)で、**評価指標として使用する損失関数(誤差関数、目的関数、Loss Function)**の設定や、**最適化アルゴリズム(勾配法、Optimizer)**の設定しています。
また、metrics は、トレーニングのログとして誤差関数(loss)以外に出力する項目を指示するもので、トレーニングそのものに何らかの影響を与える設定ではないようです(いまいち自信なし)。
以下、これらについて詳しく見ていきます。
最適化アルゴリズム(Optimizer)の選択
compile の optimizer= 引数では、トレーニングに使用する**最適化アルゴリズム(勾配法、Optimizer)**を選択します。ここで、選択可能な Optimizer は、こちらのリファレンス から一覧をみることができます。
2020/01/03 の時点では、次の Optimizer が利用できます。なお、「深層学習の最適化アルゴリズム」を参考にアルゴリズムが発表された年も併記しています。
SGDFtrl-
Adagrad:2011年 -
RMSprop:2012年 -
Adadelta:2012年 -
Adam:2014年 -
Adamax:2015年 -
Nadam:2016年
上記の xxx を使って optimizer='xxxx' のように文字列で指定することも、optimizer=tf.optimizers.Adam() のように指定して与えることも可能です(両者で微妙に大文字小文字が違ったりするので注意、詳細はリファレンスで確認)。
チュートリアルでも採用されているように、まずは Adam から試してみるのがよいのかもしれません。無論、扱う問題やNNモデルの構造や規模により、最適な Optimizer は変わるので、より良いトレーニングをさせるためには、色々と手法を変えて試すことが要求されます。
あとで、MNISTについて、最適化アルゴリズムを変えてトレーニングする実験を行ないます。
損失関数(loss)の選択
深層学習におけるトレーニングとは、最適化問題の求解と同義です。最適化問題で言うところの目的関数が「損失関数(最小化)」、決定変数が「ニューラルネットのパラメータ(重みやバイアス)」になります。
損失関数は、「NNモデルによる予測値」と「正解値」を入力として、その差異・乖離度を定量化して出力する関数です。トレーニングでは、この損失関数の出力値を最小化するようにパラメータ(重みやバイアス)の調整が進みます。
MNISTのような多クラス分類問題では、通常、その損失関数として「交差エントロピー誤差(Cross Entropy Error)」という尺度を計算するものが使われます。よって、チュートリアルでも loss='sparse_categorical_crossentropy' のように交差エントロピー誤差を計算するように設定されています。なお、選択可能な損失関数は、こちら から一覧を見ることができます。
なお、交差エントロピー誤差の計算に関しては、sparse_categorical_crossentropy と categorical_crossentropy の2つがありますが、違いは以下の通りです。
-
sparse_categorical_crossentropyは、MNISTのように多クラス分類問題の正解データ(ラベル)をカテゴリ番号で与えている場合に使います。正解が「0」「4」「2」のとき、[2,7,5]のように与えている場合。 -
categorical_crossentropyは、多クラス分類問題の正解データ(ラベル)を、one-hot表現(one-hotベクトル)で与えている場合に使います。正解が「0」「4」「2」のとき、[[1,0,0,0,0,0,0,0,0,0],[0,0,0,0,1,0,0,0,0,0],[0,0,1,0,0,0,0,0,0,0]]のように与えている場合。
仮に、カテゴリが4個だったとして、正解データが $[0,1,0,0]$、予測データが $[0.1,0.6,0.2,0.1]$ だったとすれば、交差エントロピー誤差 $\mathrm{CE}$ は次のように計算できます。
\begin{align}
\mathrm{CE} &= - ( 0\times \log_{\,e} 0.1 + 1\times \log_{\,e} 0.6 + 0\times \log_{\,e} 0.2 + 0\times \log_{\,e} 0.1 ) \\
& = -\log_{\,e} 0.6 \\
& = 0.51083
\end{align}
テストデータが複数ある場合は、平均をとればOKです。ところで、正解データは、$0$ または $1$ に限られるので、複数のテストデータ($1,2,\cdots,n$)の平均交差エントロピー誤差は、シンプルに次のように計算できます。
$$ \mathrm{CE} = -\frac{1}{n} \sum_{i=1}^{n} \log_{\ e} p_{i} $$
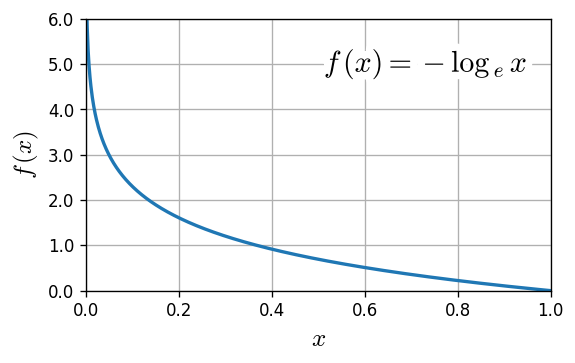
なお、$f(x) = - \log_{\ e} x $ について、$0.0 < x \le 1.0$ でプロットすると、次のようになります。
正解データと予測データが一致していれば、$-\log_{\ e}1.0=0.0$ で、CE誤差はゼロとなります。なお、$\log_{\ e}0.0=-\infty $ なのでプログラムで計算する際には工夫が必要です。
手動で交差エントロピー誤差(loss)を計算
チュートリアルのプログラムを実行すると、model.evaluate(x_test, y_test, verbose=2) のログとして次のように loss を出力してくれます。
10000/10000 - 0s - loss: 0.0734 - accuracy: 0.9775
これを自分で計算してみます。
import numpy as np
import math
s_test = model.predict(x_test) # 学習済みモデルで予測
# 交差エントロピー誤差(Cross Entropy Error)
ce = 0
n = len(y_test)
for i in range(0,n) :
ce = ce - math.log(s_test[i,y_test[i]])
ce = ce/n
print(f'CE(手計算) = {ce} ')
実行結果は以下のようになりました。
CE(手計算) = 0.07341307844041595
これは、evaluate(...) で出力された loss: 0.0734 に一致します。
最適化アルゴリズムを変えて学習、結果の比較
現時点で、TF+Keras で選択可能な8つの最適化アルゴリズム(SGD、Ftrl、Adagrad、RMSprop、Adadelta、Adam、Adamax、Nadam)で、MNISTをターゲット学習、評価を行ないました。
Epochs数=100 として、トレーニングプロセスのEpoch毎に、トレーニングデータ x_train に対する正答率(accuracy)と損失関数値(loss)、テストデータ x_test に対する正答率(val_accuracy)と損失関数値(val_loss)を取得してプロットしました。
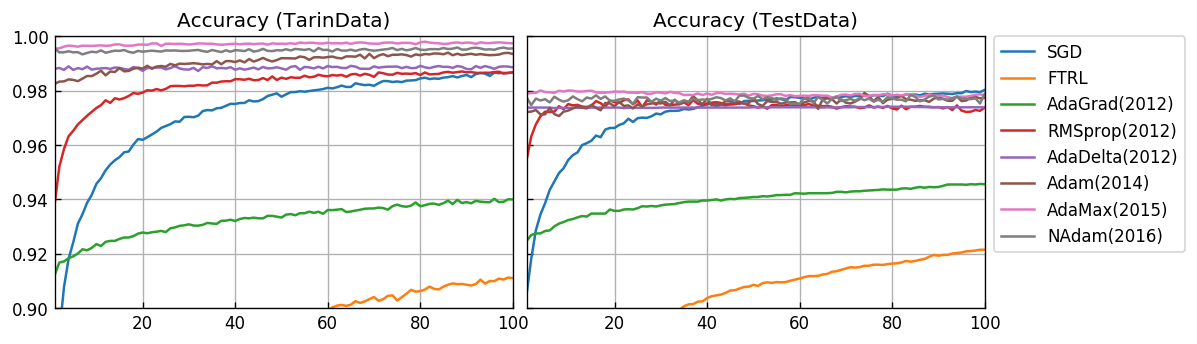
先に結果を表示します。
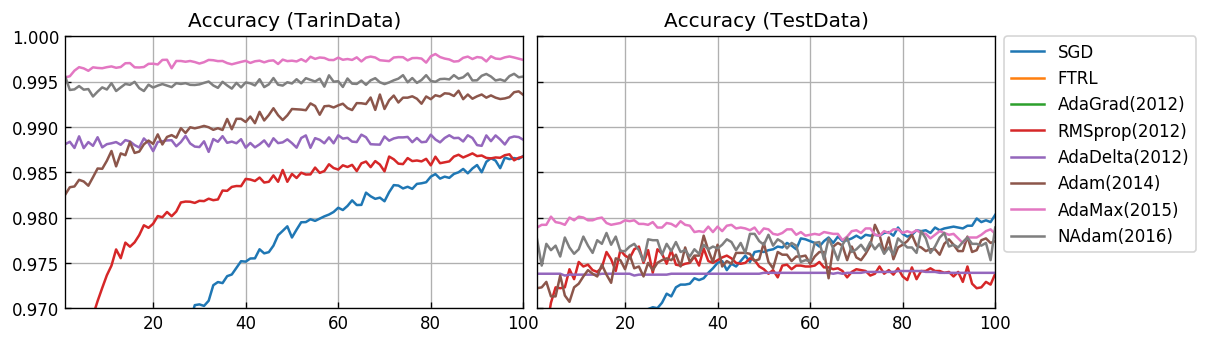
正答率(accuracy)
Y軸の範囲を拡大します。
汎化性能を考慮したテストデータに対する結果として、AdaMax(2015) が非常に優れています。SGDは、非常に時間がかかりますが、最終的には AdaMax(2015) と同じ程度の正答率が得らるモデルになっています。
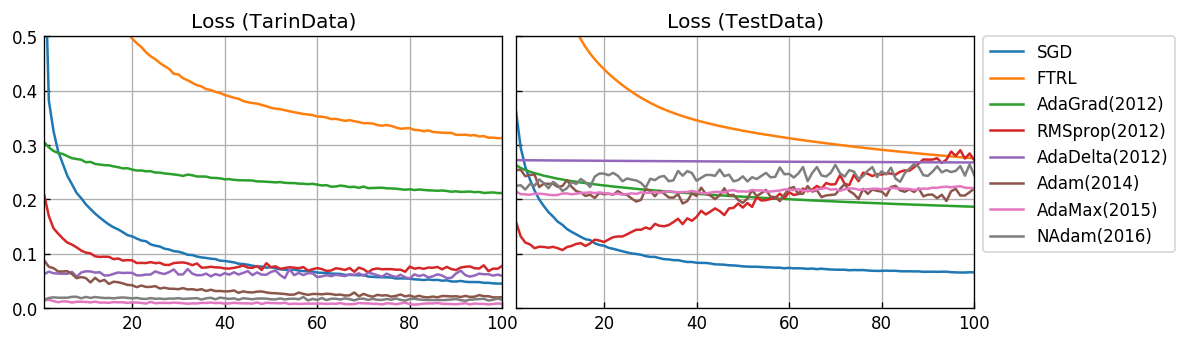
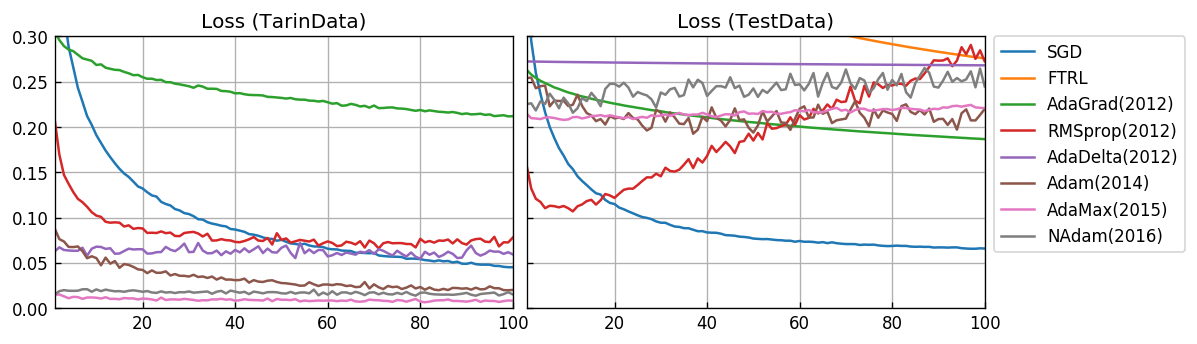
損失関数値(loss)
Y軸の範囲を拡大します。
RMSprop(2012)では、過学習を起していることが確認できます。最終的には SGD が最も優れたスコアになっています。
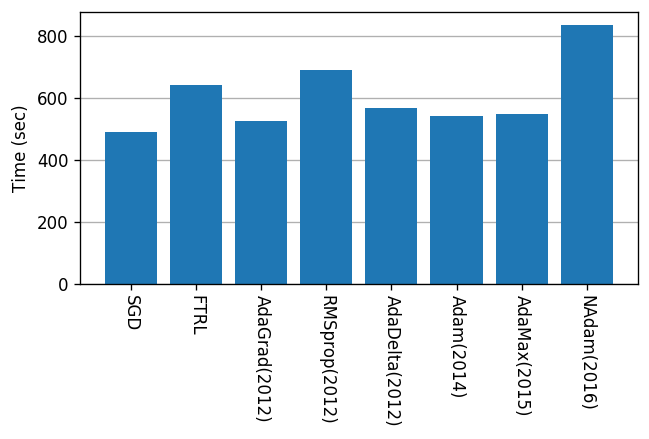
計算時間
Google Colab.環境で実行したとき、Epochs=100 に要した時間です。
(最適化手法については、完全にブラックボックスとして扱っているので下手なことは言えませんが・・・)どうも「AdaMax」が良さそうです。
プログラム
上記のグラフを求めるために使ったプログラムです。
import time
import pickle
import tensorflow as tf
tf.keras.backend.clear_session() # セッションクリア
# (1) データセットの準備
mnist = tf.keras.datasets.mnist
(x_train, y_train), (x_test, y_test) = mnist.load_data()
x_train, x_test = x_train / 255.0, x_test / 255.0
# (2) NNモデルの構築
model = tf.keras.models.Sequential()
model.add( tf.keras.layers.Flatten(input_shape=(28, 28)) )
model.add( tf.keras.layers.Dense(128, activation=tf.nn.relu) )
model.add( tf.keras.layers.Dropout(0.2) )
model.add( tf.keras.layers.Dense(10, activation=tf.nn.softmax) )
# (3) NNモデルの学習設定・学習・評価
epochs = 100
prm = [ dict(label='SGD', optm='SGD') ,
dict(label='FTRL', optm='Ftrl') ,
dict(label='AdaGrad(2012)', optm='Adagrad') ,
dict(label='RMSprop(2012)', optm='RMSprop') ,
dict(label='AdaDelta(2012)', optm='Adadelta'),
dict(label='Adam(2014)', optm='Adam') ,
dict(label='AdaMax(2015)', optm='Adamax') ,
dict(label='NAdam(2016)', optm='Nadam') ]
for p in prm :
print(f"■ 最適化アルゴリズム {p['label']}")
t = time.time()
model.compile(optimizer=p['optm'],
loss='sparse_categorical_crossentropy',
metrics=['accuracy'])
h = model.fit(x_train, y_train,
validation_data=(x_test,y_test),
epochs=epochs)
p['log'] = h.history
p['time'] = time.time() - t
p['epochs'] = epochs
results = prm
# 結果の保存
path = 'optimizer-1.pickle'
with open(path,mode='wb') as f :
pickle.dump(results,f)
import numpy as np
import matplotlib.pyplot as plt
title = dict( )
title['accuracy'] = 'Accuracy (TarinData)'
title['val_accuracy'] = 'Accuracy (TestData)'
title['loss'] = 'Loss (TarinData)'
title['val_loss'] = 'Loss (TestData)'
# 正答率
fig, ax = plt.subplots(nrows=1, ncols=2, sharey='row', figsize=(10,3), dpi=120)
plt.subplots_adjust(wspace=0.03)
for i, v in enumerate(['accuracy','val_accuracy']) :
for r in results :
ax[i].plot( range(1,r['epochs']+1),r['log'][v],label=r['label'])
ax[i].set_xlim(1,r['epochs'])
ax[i].set_ylim( 0.97,1.00 ) # ■■■要調整■■■
ax[i].set_title( title[v] )
ax[i].tick_params(which='both', direction='in')
ax[i].grid(True)
ax[1].legend(bbox_to_anchor=(1.02, 1), loc='upper left', borderaxespad=0)
plt.show()
# 損失関数値
fig, ax = plt.subplots(nrows=1, ncols=2, sharey='row', figsize=(10,3), dpi=120)
plt.subplots_adjust(wspace=0.03)
for i, v in enumerate(['loss','val_loss']) :
for r in results :
ax[i].plot( range(1,r['epochs']+1),r['log'][v],label=r['label'])
ax[i].set_xlim(1,r['epochs'])
ax[i].set_ylim( 0.0, 0.3 ) # ■■■要調整■■■
ax[i].set_title( title[v] )
ax[i].tick_params(which='both', direction='in')
ax[i].grid(True)
ax[1].legend(bbox_to_anchor=(1.02, 1), loc='upper left', borderaxespad=0)
plt.show()
# 時間
labels = list()
times = list()
for r in results :
labels.append(r['label'])
times.append(r['time'])
plt.figure(dpi=120,figsize=(6,3))
plt.bar(labels,times)
plt.ylabel('Time (sec)')
plt.xticks(rotation=-90)
plt.gca().set_axisbelow(True)
plt.grid(axis='y')
plt.show()
次回
- 次回は、モデルの学習
model.fit(...)の引数(エポック数、バッチ数、バリデーション用データ設定など)について、取り上げます。また、学習済みモデルのファイルセーブとロードについても扱っていきたいと思います。
おまけ
- 交差エントロピー誤差で使う $-\log_{,e} x$ のグラフを描くためのプログラムです。
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.ticker as tk
import matplotlib.patheffects as pe
plt.rcParams['mathtext.fontset'] = 'cm' # 数式用フォント
yt_style = lambda x, pos=None : f'{x:.1f}'
x = np.linspace(0.001, 1, 1000)
y = -np.log(x)
plt.figure(dpi=120,figsize=(5,3))
plt.plot(x,y,lw=2)
plt.xlim(0,1)
plt.ylim(0,6)
plt.gca().yaxis.set_major_formatter(tk.FuncFormatter(yt_style))
plt.xlabel('$x$',fontsize=15)
plt.grid()
plt.ylabel('$f\,(x)$',fontsize=15)
t = plt.text(0.95,5, r'$f\,(x)=-\log_{\,e}\,x$', fontsize=18,
ha='right',va='center')
t.set_path_effects([pe.Stroke(linewidth=9, foreground='white'), pe.Normal()])