Go to Qiita Advent Calendar 2024 Top
LoginSignup
3
6

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?

More than 3 years have passed since last update.

@code0327(T Wada)

TensorFlow2 + Keras による画像分類に挑戦5 ～分類に失敗する画像を観察してみる～

Last updated at Posted at 2019-12-31

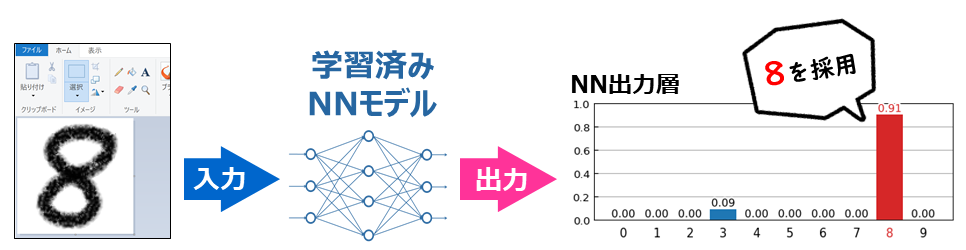
はじめに

TensorFlow2 + Keras を利用した画像分類（Google Colaboratory 環境）についての勉強メモ（第5弾）です。題材は、ド定番である手書き数字画像（MNIST）の分類です。

前回 は、学習済みモデルを使って予測（分類）を行ないました。今回は、TF公式HPのチュートリアル で作成するモデルで、**予測（分類）に失敗する画像はどんなものか？**また、**どんな誤分類が生じるのか？**を観察していきます。

具体的には、matplotlib で、次のような出力をしていきます

■ 正解値「6」に対して正しく予測（分類）できなかったケース
x6.png

また、次のような誤分類の関係を表した図も作成していきます。

ヒートマップ.png

分類に失敗した手書き数字データの抽出

テスト用の入力データ（手書き数字のイメージ）10,000件のうち、TFチュートリアルのモデルを使って正しく分類できなかったものを抽出していきます。

ところで、学習済みモデルについて、model.evaluate(x_test, y_test, verbose=2) で評価したところ 正解率（accuracy）が 0.9759 になりました。よって、$(1-0.9759)\times 10,000=241$ 枚の手書き数字が分類に失敗しています（学習の実行毎に生成される学習済みモデルは僅かに違ってくるので、その結果、分類に失敗する画像も微妙に違ってきますので留意ください）。

この抽出処理には、データ分析に便利なライブラリ「pandas」を使用します。なお、pandas の基礎についての解説は含めないので、そのあたりは他の記事を参考にしてください。

次のようなコードで、データフレームの列に正解値と予測値を格納します。ここで、行のインデックスは、x_test のインデックスと一致します。

import numpy as np
import pandas as pd
p_test = model.predict_classes(x_test) # 予測
df = pd.DataFrame({'正解値':y_test, '予測値':p_test})
display(df.head(5))  # 先頭から5行を表示
display(df.tail(5))  # 末尾から5行を表示

実行結果は、次のようになります。先頭から5件、末尾から5件については、正解値と予測値が全て一致しています。

pd1.png

つづいて、正解値と予測値が一致していない行を抽出して新たなデータフレーム df2 に格納します。また、ソートもかけます。

# 「正解」と「予測」が一致していない行を抽出
df2 = df[df['正解値']!=df['予測値']]
display(df2.head(5))

# 昇順にソート 第1キー'正解値'、第2キー'予測値'
df2 = df2.sort_values(['正解値', '予測値'])
display(df2.head(5))

実行結果は、次のようになります。
pd2.png

これより、x_test[9634] は「正解は「0」であるが、予測は「1」となった」ということが分かります。

分類に失敗した手書き数字画像の一覧表示

分類に失敗した x_test[9634] は、どんな手書き数字なのか、また、**誤って「1」と予測しているが、それはどの程度の確信によるものだったのか？**が気になりますよね。

どんな手書き数字なのかは、第2回で解説したように matplotlib の imshow(...) を使えば画像出力して確認できます。

また、誤って「1」と予測したのはどの程度の確信によるものだったのかは、第4回 で解説したように、model.predict(...) で得られる情報のなかから取り出すことができます。具体的には次のようにすれば、求めることができます。

idn = 9634
s = model.predict( np.array([x_test[idn]]) ) # 出力層の値
s = s[0]
print( f'予測分類は「{s.argmax()}」で、出力層の対応ニューロンの出力値{s[s.argmax()]:.2f}' ) 
print( f'正解分類は「{y_test[idn]}」で、出力層の対応ニューロンの出力値{s[y_test[idn]]:.2f}' )

予測分類は「1」で、出力層の対応ニューロンの出力値0.62
正解分類は「0」で、出力層の対応ニューロンの出力値0.00

あるいは、第4回 の最後で示したコード（予測分類のレポート出力）を使えば、次のようにも確認できます。

9634.png

正解である「0」には、かすってもいませんね。左上にゴミが載っている画像なので、仕方ないのかもしれませんが・・・こういったことを観察できれば、前処理に関する何らかのヒントを得られる可能性があります。

しかし、これらを個別に出力するは手間なので、まとめて出力してみたいと思います。

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.patheffects as pe

for t in range(0,10):

  print(f'■ 正解値「{t}」に対して正しく予測（分類）できなかったケース')

  # 正解値が t の行を抽出
  index_list = list(df2[df2['正解値']==t].index.values)

  # matplotlib 出力
  n_cols = 7
  n_rows = ((len(index_list)-1)//n_cols)+1
  fig, ax = plt.subplots(nrows=n_rows, ncols=n_cols, figsize=(6.5, 0.9*n_rows), dpi=120)
  for i,ax in enumerate( np.ravel(ax) ):
    if i < len(index_list):
      
      p = index_list[i]
      ax.imshow(x_test[p],interpolation='nearest',vmin=0.,vmax=1.,cmap='Greys')

      # 予測（分類）を左上に表示
      t = ax.text(1, 1, f'{p_test[p]}', verticalalignment='top', fontsize=8, color='tab:red')
      t.set_path_effects([pe.Stroke(linewidth=2, foreground='white'), pe.Normal()]) 

      # 予測（分離）に対応する出力層のニューロンの値を括弧で表示
      t = ax.text(5, 2, f'({s_test[p].max():.1f})', verticalalignment='top', fontsize=6, color='tab:red')
      t.set_path_effects([pe.Stroke(linewidth=2, foreground='white'), pe.Normal()]) 
      
      # 目盛などを非表示に
      ax.tick_params(axis='both', which='both', left=False, labelleft=False, 
                     bottom=False, labelbottom=False)
      
      # 青色でインデックスを表示
      ax.set_title(index_list[i],fontsize=7,pad=1.5,color='tab:blue')

    else :
      ax.axis('off') # 余白処理

  plt.show()

実行結果です（テキストで出力される部分のみ少し整形しています）。

  • 各画像枠の上部の水色の番号がx_test のインデックス番号
  • 画像内の左上部の**赤色の数字**が、予測値（つまり、誤って予測（分類）した値）
  • 画像内の左上部の赤色の数字が、出力層の上記に対応するニューロンの出力値
  • 例えば、最初の例では「1 (0.6)」となっていますが、これは（誤って）「1」と分類しており、出力層の「1」に対応するニューロンの出力値が「0.6」であった、という意味です。

■ 正解値「0」に対して正しく予測（分類）できなかったケース
x0.png

■ 正解値「1」に対して正しく予測（分類）できなかったケース
x1.png

■ 正解値「2」に対して正しく予測（分類）できなかったケース
x2.png

■ 正解値「3」に対して正しく予測（分類）できなかったケース
x3.png

■ 正解値「4」に対して正しく予測（分類）できなかったケース
x4.png

■ 正解値「5」に対して正しく予測（分類）できなかったケース
x5.png

■ 正解値「6」に対して正しく予測（分類）できなかったケース
x6.png

■ 正解値「7」に対して正しく予測（分類）できなかったケース
x7.png

■ 正解値「8」に対して正しく予測（分類）できなかったケース
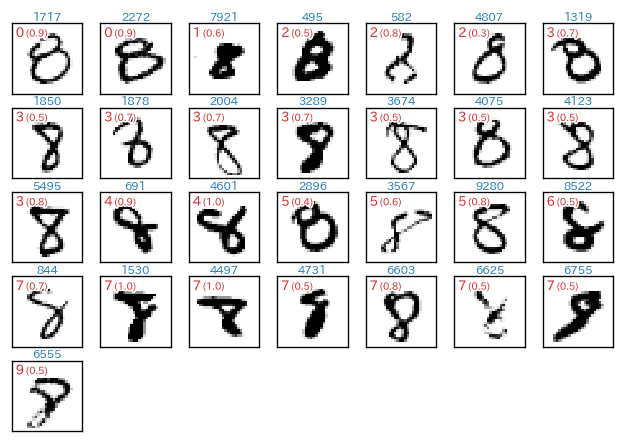
x8.png

■ 正解値「9」に対して正しく予測（分類）できなかったケース
x9.png

感想

こうやって眺めてみると、どう考えても認識不可能なデータ（たとえ人間が判断しても・・・）も混じっているということが分かります。その一方で、人間的な感覚から言えば、なんでそんな誤認識するの？という結果もあります。興味深いですね。

クロス集計表

正解値と予測値についてのクロス集計表を作成してみます。これにより**どの数字を、どの数字に誤分類しやすいのか？**といった情報を得ることができます。クロス集計は、crosstab(...) で簡単に作成できます。

import pandas as pd

p_test = model.predict_classes(x_test) # 予測
df = pd.DataFrame({'正解値':y_test, '予測値':p_test})

# クロス集計表
dfc = pd.crosstab(index=df['正解値'], columns=df['予測値']) 
display(dfc)

実行結果は次のようになります。

ct.png

「4」を「9」に誤分類するケースが 19件 で一番多いようです（なんとなく分かりますね）。次いで「3」を「5」に誤分類するのが 13件、「9」を「3」に誤分類するのが 12件 になっています（これは、人間的な感覚とは違っていて面白いところですね）。

ビジュアル化

クロス集計表を matplotlib を使ってヒートマップ的に出力してみます。コードが長くなるので先に結果を示します。

ヒートマップ.png

matplotlib_日本語出力準備処理
!pip install japanize-matplotlib
import japanize_matplotlib

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.patheffects as pe
import matplotlib.ticker as ticker
import matplotlib.colors

p_test = model.predict_classes(x_test) # 予測
df = pd.DataFrame({'正解値':y_test, '予測値':p_test})

# クロス集計表
dfc = pd.crosstab(index=df['正解値'], columns=df['予測値']) 
#display(dfc)

for i in dfc.index.values :
  dfc.at[i,i] = 0.0

# ヒートマップ的に出力
plt.figure(dpi=160)

plt.imshow(dfc,interpolation='nearest',cmap='Oranges')
plt.plot([0,0],[9,9])

n = len(dfc.columns) # 項目数
plt.gca().set_xticks(range(n))
plt.gca().set_xticklabels(dfc.columns)
plt.gca().set_yticks(range(n))
plt.gca().set_yticklabels(dfc.columns)

plt.tick_params(axis='x', which='both', direction=None, 
                top=True, bottom=False, labeltop=True, labelbottom=False)
plt.tick_params(axis='both', which='both', top=False, left=False )

# グリッドに関する設定
plt.gca().set_xticks(np.arange(-0.5, n-1), minor=True);
plt.gca().set_yticks(np.arange(-0.5, n-1), minor=True);
plt.grid( which='minor', color='white', linewidth=1)

plt.gca().xaxis.set_label_position('top') 
plt.xlabel('予測値')
plt.ylabel('正解値')

plt.plot([-0.5,n-0.5],[-0.5,n-0.5],color='black',linewidth=0.75)

# 相関係数を表示（文字に縁取り付き）
tp = dict(horizontalalignment='center',verticalalignment='center')
ep = [pe.Stroke(linewidth=3, foreground='white'),pe.Normal()]
for y,i in enumerate(dfc.index.values) :
  for x,c in enumerate(dfc.columns.values) :
    if x != y :
      if dfc.at[i,c] !=  0:
        t = plt.text(x, y, f'{dfc.at[i,c]}',**tp)
        t.set_path_effects(ep)

次回

  • 次回は、自分で作成した手書きでデータを入力とした予測を行ないます。Google Colab. に画像をアップする手順、画像の読込み、リサイズ、その他の前処理などを含みます。

予測.png

3
6
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
3
6

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?