はじめに
TensorFlow2 + Keras を利用した画像分類(Google Colaboratory 環境)についての勉強メモ(第3弾)です。題材は、ド定番である手書き数字画像(MNIST)の分類です。
- TensorFlow2 + Keras による画像分類に挑戦 シリーズ
前回は、MNISTデータを取得し、そのデータの構造や内容について確認しました。手書きの数字の画像データに相当する入力データは、28x28pixelの256段階グレースケールでした。このデータの型は numpy.ndarray の2次元配列で、そのまま print するだけでも、なんとか内容(画像イメージ)をつかむことができましたが、今回は matplotlib を使って、次のようにきれいに表示させてみたいと思います。
データの正規化
MNISTのデータは、0~255の整数値を使って、256段階グレースケール(白を0、黒を255に割り当てたグレースケール)を表現していました(詳しくは前回参照)。しかし、TensorFlow を使った画像分類のサンプルコード(公式HPのチュートリアル参照)では、機械学習させる都合上、次のように 0.0~1.0 の範囲になるように正規化を施しています。
import tensorflow as tf
mnist = tf.keras.datasets.mnist
(x_train, y_train), (x_test, y_test) = mnist.load_data()
x_train, x_test = x_train / 255.0, x_test / 255.0 # 正規化処理
ここから先は、0.0~1.0 に正規化されたデータを対象に進めていきたいと思います。
とりあえず表示
トレーニング用の入力データの1個目 x_train[0] をグレースケール画像として出力してみたいと思います。このデータは、正解データ y_train[0] に格納されているように「5」を表現した画像になります。
import matplotlib.pyplot as plt
plt.figure(dpi=96)
plt.imshow(x_train[0],interpolation='nearest',vmin=0.,vmax=1.,cmap='Greys')
実行環境によっては、interpolation='nearest'は省略できます(Google Colab.では省略してもOKです、他環境で実行してぼやけた出力になったら、このオプションを明示しましょう)。
また、vmin=0.,vmax=1. は、当該データ x_train[?] の内部要素の最小値が 0.0、最大値が 1.0 の場合は省略してもOKです(cmap='Greys' により0.0に白、1.0に黒が割り当てられます)。そうでない場合、例えば、薄文字などを表現していてx_train[?]の内部要素の最大値が0.7のようなときは、このオプションを指定しないと、薄文字の感じが反映されません。
キーワード引数 cmap の値を変えると、出力に使用するカラーマップを変えることができます。プリセットとして用意されているカラーマップ一覧は、matplotlibのリファレンスで確認することができます。例えば、cmap='Greens'とすると次のような出力になります(0.0のところも薄緑になります)。
カラーマップをカスタマイズすることも可能です。具体的な方法は「相関行列をキレイにカスタマイズしたヒートマップで出力したい。matplotlib編 @ Qiita」を参照ください。
特定の数字についての手書き画像を並べて出力
特定の数字(例えば「7」)について、どんなで手書きデータが存在するのか確認したいときには、次のようなコードで出力することができます。
import numpy as np
import matplotlib.pyplot as plt
x_subset = x_train[ y_train == 7 ] # (1)
fig, ax = plt.subplots(nrows=8, ncols=8, figsize=(5, 5), dpi=120)
for i, ax in enumerate( np.ravel(ax) ):
ax.imshow(x_subset[i],interpolation='nearest',vmin=0.,vmax=1.,cmap='Greys')
ax.tick_params(axis='both', which='both', left=False,
labelleft=False, bottom=False, labelbottom=False) # (2)
実行結果は次のようになります。7以外の数値について出力したい場合は、上記コードの (1) の y_train == 7 の数値を変更してください。(2) の ax.tick_params(...) は、X軸・Y軸の目盛を消すためのものです。
一覧で眺めてみると、この64枚のなかであっても、どうみても「1」にしか見えないものが少なくとも2、3個は含まれているということが分かります(つまり、正答率 1.0000 は極めて難しい)。
整形して表示
非常に短いコードで入力データを画像化して出力できることが分かりました。
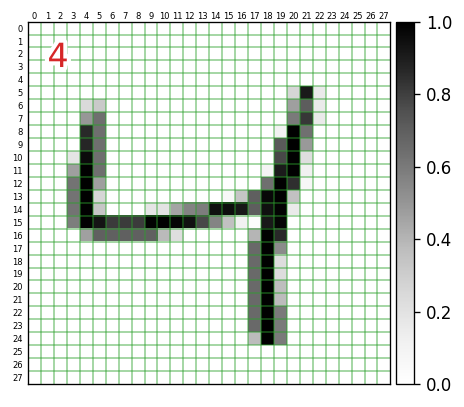
ここでは、次のように、各入力データの何行何列目の要素がどんな値になっているのか?までを確認できるように手を加えていきます。左上の赤文字は、対応する正解データの値です。
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.patheffects as pe
import matplotlib.transforms as ts
i = 2 # 表示するデータのインデックス
plt.figure(dpi=120)
plt.imshow(x_train[i],interpolation='nearest',vmin=0.,vmax=1.,cmap='Greys')
h, w = 28, 28
plt.xlim(-0.5,w-0.5) # X軸方向の描画範囲
plt.ylim(h-0.5,-0.5) # Y軸方向の・・・
#
plt.tick_params(axis='both', which='major',
left=False, labelleft=False,
bottom=False, labelbottom=False)
plt.tick_params(axis='both', which='minor',
left=False, labelleft=True,
top=False, labeltop=True,
bottom=False, labelbottom=False)
# 各軸のグリッド設定
plt.gca().set_xticks(np.arange(0.5, w-0.5,1)) # 1ドット単位でグリッド
plt.gca().set_yticks(np.arange(0.5, h-0.5,1))
plt.grid( color='tab:green', linewidth=1, alpha=0.5)
# 各軸のラベル設定
plt.gca().set_xticks(np.arange(0, w),minor=True)
plt.gca().set_xticklabels(np.arange(0, w),minor=True, fontsize=5)
plt.gca().set_yticks(np.arange(0, h),minor=True)
plt.gca().set_yticklabels(np.arange(0, h),minor=True, fontsize=5)
# ラベルの位置の微調整
offset = ts.ScaledTranslation(0, -0.07, plt.gcf().dpi_scale_trans)
for label in plt.gca().xaxis.get_minorticklabels() :
label.set_transform(label.get_transform() + offset)
offset = ts.ScaledTranslation(0.03, 0, plt.gcf().dpi_scale_trans)
for label in plt.gca().yaxis.get_minorticklabels() :
label.set_transform(label.get_transform() + offset)
# 正解データを左上に表示(白色で縁取り)
t = plt.text(1, 1, f'{y_train[i]}', verticalalignment='top', fontsize=20, color='tab:red')
t.set_path_effects([pe.Stroke(linewidth=5, foreground='white'), pe.Normal()])
plt.colorbar( pad=0.01 ) # 右側にカラーバー表示
グレースケール値のヒストグラム
入力データは、$28\times 28 = 784$ 個の要素から構成され、各要素には 0.0 から 1.0 の値が含まれますが、それはどんな分布になっているかヒストグラムを作成してみたいと思います。
import numpy as np
import matplotlib.pyplot as plt
i = 0 # 表示するデータのインデックス
h = plt.hist(np.ravel(x_train[i]), bins=10, color='black')
plt.xticks(np.linspace(0,1,11))
print(h[0]) # 実行結果 -> [639. 11. 6. 11. 6. 9. 11. 12. 11. 68.]
print(h[1]) # 実行結果 -> [0. 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1. ]
plt.hist(...) の戻値には、各階級の度数が含まれます。上記の例だと、範囲 $0.0\le v < 0.1 $ の値を持つピクセルが 639個存在することが分かります。なお、一番右端のみ、範囲は $0.9\le v \le 1.0 $ となり、値がちょうど 1.0 のデータも含んだものになります。
実際に print(h[0].sum()) にすれば、784.0 が得られ、値がちょうど 1.0 の要素もちゃんとカウントされていることが確認できます。
次回
- 学習済みのモデルを使って実際に予測を行ないます。