最適化アルゴリズムを単独実行で比較する(Adagrad/RMSprop/Adadelta編)

はじめに

この記事では、数式は使わず、実際のコードから翻訳した疑似コードを使って動作を紹介する。また、Keras(TensorFlow)のOptimizerを使用した実験結果を示すことにより、各種最適化アルゴリズムでのパラメーターの効果や、アルゴリズム間の比較を行う。

ここでは、Adagrad/RMSprop/Adagradを扱う。
SGD編
Adam/Adamax/Nadam編
FTRL編
総合編

実験方法

極簡単なネットワークを学習させ、学習過程をグラフにプロットして比較する。
具体的には、下記の内容。

• 初期値1.0、最適値0.0として、Optimiserのminimize()を直接実行し、ステップ毎に最適値に近づく様子を観察する。
• 損失関数は特に言及しない限り絶対値(MAE)を使用。場合によっては二乗(MSE)なども使用。
• Keras使用。Google Colabで実行可な実験コードを最後に記載。

Adagrad

MomenumSGDでは慣性項を導入することで学習を加速させた。
Adagradやその派生アルゴリズムは、基本的には学習率(勾配に掛ける係数)を適応的に変動させることで、学習を早めたり振動を抑える。

Adagradの論文。
Adaptive Subgradient Methods for Online Learning and Stochastic Optimization

Keras実装は以下を参照した。
keras/optimizers.py
TensorFlow API Adagrad

Adagradにおける設定可能なパラメーターは以下の通り。

パラメーター	範囲	初期値	説明
learning_rate	float >= 0	0.001	Learning rate.
initial_accumulator_value	float >= 0	0.1	Starting value for the accumulators
epsilon	float >= 0	1e-8	Fuzz factor.

内部処理を翻訳すると以下のようなコードになっている。

def get_step(grad):
  self.accumlator = self.accumlator + (grad**2)
  v = -lr * grad / ( (self.accumlator**0.5)+self.epsilon )
  return v

イテレーションごとにaccumelatorは確実に増加していく。lr / (accumulator**0.5)を修正学習率と解釈すれば、学習が進むと絶対に学習率が下がることになる。
SGDでもDecayを使えば学習率が下がるが、Adagradは実際の勾配をみて「適応的に学習率が減る」と解釈できる。
initial_accumulator_valueはaccumlatorの初期値。
epsilonは勾配が非常に小さい場合に不安定になることを防ぐためのもの。

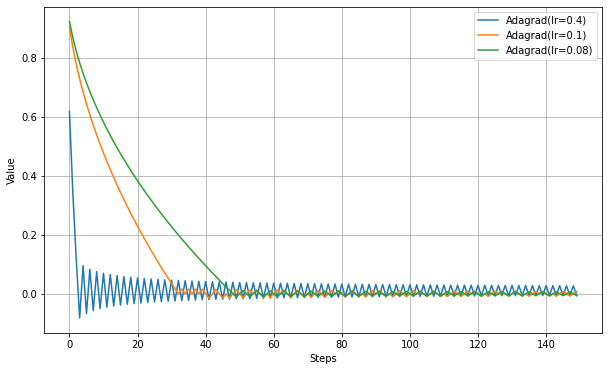
以下、学習率の違いを見る実験。

最適値付近で振動するが、振幅が徐々に小さくなっていることがわかる。

以下、initial_accumulator_valueの違いを見る実験。

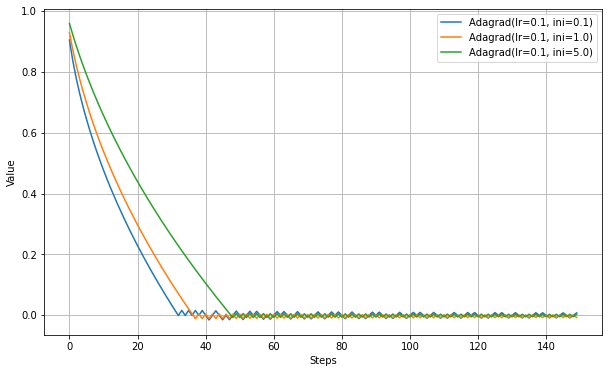
initial_accumulator_valueを大きくすると、学習が遅くなる。これは修正学習率が最初から小さくなるためだろう。

RMSprop

Adagradでは、勾配が積算される一方なので、一度大きな勾配を経験するとその後の学習率が相対的に低くなりすぎる問題がある。実際の機械学習では勾配が0付近になる地点が複数あることが見込まれるので、最適解に到達する前に学習が止まってしまう可能性が高くなる。
「過去の勾配情報を忘却させていく」という手法でこの問題の緩和を目指したものがRMSpropとなる。
Adagradとの違いは、accumlatorの計算で単純に加算するのではなく、移動二乗平均平方根(moving RMS)としていることにある。これにより、学習が進むにつれて修正後の学習率が一方的に小さくなることを防ぐ。

Keras実装は以下を参照した。
keras/optimizers.py
training_ops.cc
Tensorflow API RMSprop

RMSpropの論文
rmsprop: Divide the gradient by a running average of its recent magnitude

RMSpropにおける設定可能なパラメーターは以下の通り。

Paramater	Range	Default	Description
lr	float >= 0	0.001	Learning rate.
rho	float >= 0	0.9	Discounting factor for the history/coming gradient.
momentum	float >= 0	0.0	Momentum
epsilon	float >= 0	1e-8	A small constant for numerical stability.
centered	Boolean	False	If True, gradients are normalized by the estimated variance of the gradient; if False, by the uncentered second moment. Setting this to True may help with training, but is slightly more expensive in terms of computation and memory.

内部処理を翻訳すると以下のようなコードになっている。

def get_step(grad):
  self.accumlator = (self.rho*self.accumlator) + (1.0-self.rho)*(grad**2)
  if centered:
    self.mg = (self.rho*self.mg) + (1.0-self.rho)*grad
    denominator = self.accumlator - (self.mg**2) + epsilon
  else:
    denominator = self.accumlator + epsilon
  self.mom = self.mom*momentum + lr*grad/(denominator**0.5)
  v = -self.mom
  return v

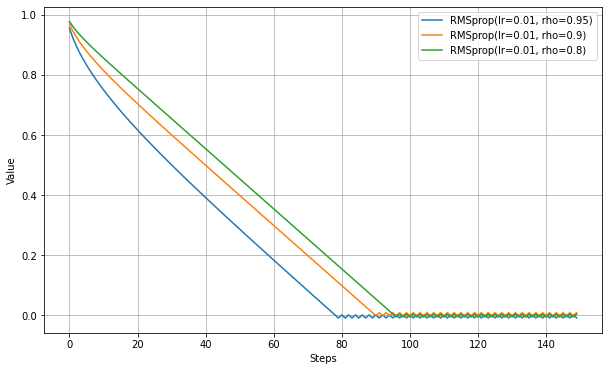
rhoは指数移動平均の係数で大きいほど過去の勾配を重要視する。
momentumはMomentumSGDで導入した慣性項と同じ機能。RMSpropの改良版であるAdamは「RMSpropにMomentumを追加したもの」と表現されることがあるようだが、こちらの実装はAdamとは別ものである。MomentumSGDとの関連でいえば、Adamよりもこちらのほうが素直に慣性項を追加した実装となっているように思われる。
centeredは「指数移動平均の中心値を補正するかどうか」、の設定と思われ、これはRMSpropGravesと呼ばれる改良版のようだ。

Adagradとの差がわかりやすいようにmomentumとcenteredを抜くと以下のような処理。

def get_step(grad):
  self.accumlator = (self.rho*self.accumlator) + (1.0-self.rho)*(grad**2)
  v = -lr * grad / ( (self.accumlator**0.5)+self.epsilon )
  return v

以下、lrだけ変更して実験。

Adagradと似たような動作になるが、Adagradでは振動は減衰していくことに比べると、RMSpropでは同様の減衰は見られない。指数移動平均により、古い勾配の寄与がなくなるため、一方的に減衰しなくなる効果が出ている。

以下、centeredをTrueにして実験(RMSpropGraves)。

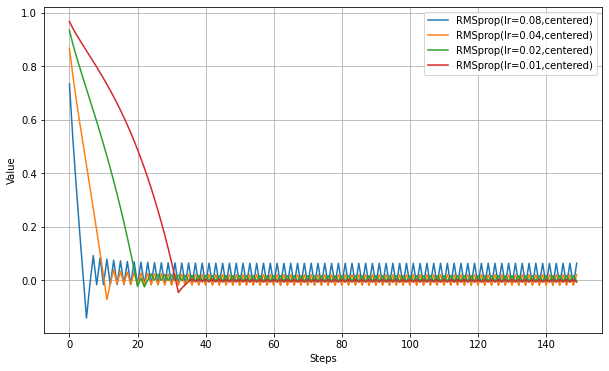
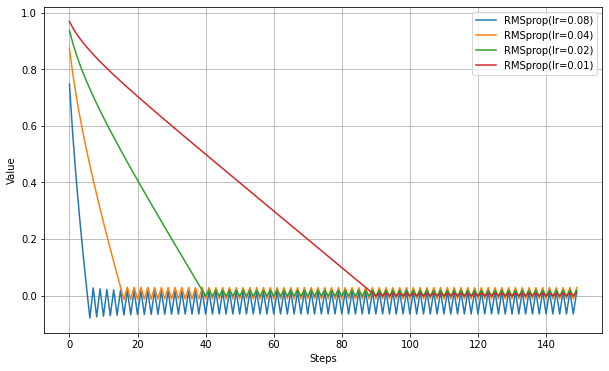
学習が速くなっている。

以下、momentumを設定して実験。

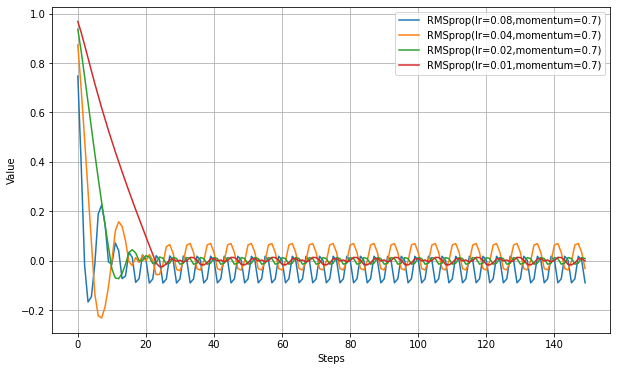
学習が速くなっている代わりに、最適値付近での振幅がやや増えているようだ。MomentumSGDと似ている。

以下、rhoを変えた場合の違いの実験。

Adadelta

Adagradから派生したアルゴリズム。
RMSprop同様に、指数移動平均を使用して、過去の勾配を忘れる。違うところは、適応学習率の計算で過去のステップサイズの指数移動平均を掛けていることで、勾配が大きい場合と小さい場合の学習率の効果の差を軽減しているようだ。これにより学習率の設定が不要になった、と元論文では言っている模様。

Keras実装は以下を参照した。
keras/optimizers.py
Tensorflow API Adadelta

Adadeltaの論文
Adadelta - an adaptive learning rate method

Adadeltaにおける設定可能なパラメーターは以下の通り。

Paramater	Range	Default	Description
lr	float >= 0	0.001	Learning rate.
rho	float >= 0	0.95	The decay rate.
epsilon	float >= 0	1e-7	A constant epsilon used to better conditioning the grad update.
decay	float >= 0	0	Learning rate decay over each update.

内部処理を翻訳すると以下のようなコードになっている。

def get_step(grad):
  lr = self.lr * (1. / (1. + self.decay * iterations))
  self.accumlator = (self.rho*self.accumlator) + (1.0-self.rho)*(grad**2)
  update = grad * (self.delta_accumulator+self.epsilon)**0.5) / ((self.accumlator+self.epsilon)**0.5)
  self.delta_accumulator = (self.rho*self.delta_accumulator) + (1.0-self.rho)*(update**2)
  v = -lr * update
  return v

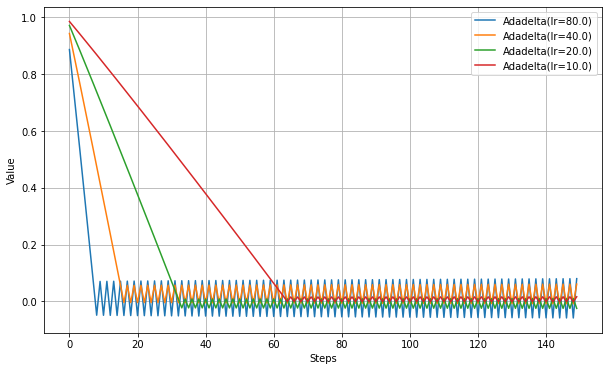
Adadeltaの特徴としてハイパーパラメータとしての学習率の調整が必要ない、と言われるが、実際にはlrが存在する。元論文と同じ設定にしたいならlr=1.0とせよ、とありこの場合は学習率を設定していないことにはなるかもしれない。

以下、lrを変えて実験。

他のアルゴリズムに比べlrに大幅に大きな値を設定しないと、同じ程度のステップ数では最適解に到達しない。少なくとも学習率の調整が必要な場合もあるということは言えそうだ。

Adadeltaには下記の注意書きがある。

According to section 4.3 ("Effective Learning rates"), near the end of training step sizes converge to 1 which is effectively a high learning rate which would cause divergence. This occurs only near the end of the training as gradients and step sizes are small, and the epsilon constant in the numerator and denominator dominate past gradients and parameter updates which converge the learning rate to 1.

学習の終わり付近で勾配が0に近づくとステップサイズが1に収束してしまうため、学習率が大きくなりすぎて発散する可能性がある、ということらしい。

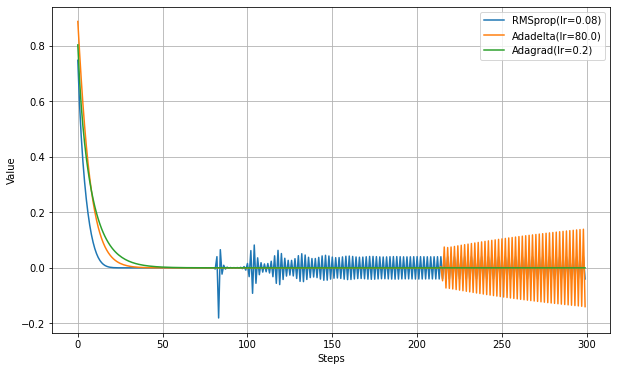
損失関数がMAEでは勾配が0にならないので、MSEで実験する。RMSpropとAdagradの結果も載せる。

RMSpropが70step辺りで不安定になっている。これは分母が非常に小さくなって勾配の変化に敏感になっているためと思われる。
Adadeltaは220step辺りで発散が開始しているようだ。不安定になるまでのステップ数はRMSpropより長いので、より安定していると評価できるかもしれない。ただし発散はRMSpropより激しい。
Adagradにはこのような現象は見られない。

まとめ

• Adagradは学習途中で学習率が減少しすぎて最適値に到達できない可能性がある。
• RMSpropはかなり高速に最適値へ向かう。Adagradと違い途中で学習率が一方的に減少することがないが、最適値付近での振動は止まらない。
• Keras/TensorFlowのRMSpropはmomentumとcenteredのパラメータがある。momentumを設定するとさらに高速になる。
• Adadeltaは学習率を他の最適化手法よりもかなり大きく設定しなければならない。また、最適値近くでは大きく発散する可能性がある。

条件が単純すぎたので、各アルゴリズムの違いが大きく出なかった可能性もある。もうすこし複雑な条件での比較は別記事で行うことにする。

#参考

深層学習の最適化アルゴリズム
勾配降下法一覧 (2020)
RMSpropGravesについて自分なりに考えてみた

実験コード

TestOptimizer.py

import numpy as np
import tensorflow as tf
import matplotlib.pyplot as plt

from tensorflow.keras.optimizers import SGD,RMSprop,Adagrad,Adadelta,Adam


def testOptims(optims, lossFn='mae', total_steps=150):
    fig = plt.figure(figsize=(10,6),facecolor="white",)
    ax = fig.add_subplot(111)

    steps = range(total_steps)
    y = np.zeros(total_steps)
    if lossFn=='mae':
        loss = lambda: tf.abs(var1)
    elif lossFn=='mse':
        loss = lambda: var1**2

    for label, optim in optims.items():
        var1 = tf.Variable(1.0)
        for i in range(total_steps):
            optim.minimize(loss, [var1]).numpy()
            y[i] = var1.numpy()
        ax.plot( steps, y, label=label )
    
    ax.legend(bbox_to_anchor=(1.0,1.0))        
    ax.set_xlabel('Steps')
    ax.set_ylabel('Value')
    ax.grid()
    plt.show()
print('Adagrad(lr)')
testOptims(
    {
        'Adagrad(lr=0.4)': Adagrad(0.4),
        'Adagrad(lr=0.1)': Adagrad(0.1),
        'Adagrad(lr=0.08)': Adagrad(0.08),
    },
    lossFn = 'mae' ,
)

print('Adagrad(initial_accumulator_value)')
testOptims(
    {
        'Adagrad(lr=0.1, ini=0.1)': Adagrad(0.1, initial_accumulator_value=0.1),
        'Adagrad(lr=0.1, ini=1.0)': Adagrad(0.1, initial_accumulator_value=1.0),
        'Adagrad(lr=0.1, ini=5.0)': Adagrad(0.1, initial_accumulator_value=5.0),
    },
    lossFn = 'mae',
)

print('RMSprop(lr)')
testOptims(
    {
        'RMSprop(lr=0.08)': RMSprop(0.08),
        'RMSprop(lr=0.04)': RMSprop(0.04),
        'RMSprop(lr=0.02)': RMSprop(0.02),
        'RMSprop(lr=0.01)': RMSprop(0.01),
    },
    lossFn = 'mae',
)
print('RMSprop(centered)')
testOptims(
    {
        'RMSprop(lr=0.08,centered)': RMSprop(0.08, centered=True),
        'RMSprop(lr=0.04,centered)': RMSprop(0.04, centered=True),
        'RMSprop(lr=0.02,centered)': RMSprop(0.02, centered=True),
        'RMSprop(lr=0.01,centered)': RMSprop(0.01, centered=True),
    },
    lossFn = 'mae',
)
print('RMSprop(momentum)')
testOptims(
    {
        'RMSprop(lr=0.08,momentum=0.7)': RMSprop(0.08,momentum=0.7),
        'RMSprop(lr=0.04,momentum=0.7)': RMSprop(0.04,momentum=0.7),
        'RMSprop(lr=0.02,momentum=0.7)': RMSprop(0.02,momentum=0.7),
        'RMSprop(lr=0.01,momentum=0.7)': RMSprop(0.01,momentum=0.7),
    },
    lossFn = 'mae',
)
print('RMSprop(rho)')
testOptims(
    {
        'RMSprop(lr=0.01, rho=0.95)': RMSprop(0.01, rho=0.95),
        'RMSprop(lr=0.01, rho=0.9)': RMSprop(0.01, rho=0.90),
        'RMSprop(lr=0.01, rho=0.8)': RMSprop(0.01, rho=0.80),
    },
    lossFn = 'mae',
)
print('Adadelta(lr)')

testOptims(
    {
        'Adadelta(lr=80.0)': Adadelta(80.0),
        'Adadelta(lr=40.0)': Adadelta(40.0),
        'Adadelta(lr=20.0)': Adadelta(20.0),
        'Adadelta(lr=10.0)': Adadelta(10.0),
    },
    lossFn = 'mae' 
)

print('RMSprop(mse)')
testOptims(
    {
        'RMSprop(lr=0.08)': RMSprop(0.08),
        'Adadelta(lr=80.0)': Adadelta(80.0),
        'Adagrad(lr=0.2)': Adagrad(0.2),
    },
    lossFn = 'mse',
    total_steps=300
)