最適化アルゴリズムを単独実行で比較する(FTRL編)

はじめに

この記事では、実際のコードから翻訳した疑似コードを使って動作を紹介する。また、Keras(Tensorflow)のOptimizerを使用した実験結果を示すことにより、各種最適化アルゴリズムでのパラメーターの効果や、アルゴリズム間の比較を行う。

ここでは、FTRLを扱う。
SGD編
Adagrad/RMSprop/Adadelta編
Adam/Adamax/Nadam編
総合編

実験方法

極簡単なネットワークを学習させ、学習過程をグラフにプロットして比較する。
具体的には、下記の内容。

• 初期値1.0、最適値0.0として、Optimiserのminimize()を直接実行し、ステップ毎に最適値に近づく様子を観察する。
• 損失関数は特に言及しない限り絶対値(MAE)を使用。場合によっては二乗(MSE)なども使用。
• Keras使用。Google Colabで実行可な実験コードを最後に記載。

Ftrl

FTRLは'Follow The (Prox-imally) Regularized Leader'の頭文字をとったもの。
広告で収益を上げるタイプのビジネスで重要な'ad Click–Through Rates'を予測するための研究で開発されたようだ。
TensorFlowやPyTorchで標準実装されているにも関わらず、あまり情報がない。

ftrl.py
training_ops.cc
Tensorflow API Ftrl

元論文
paper

Ftrlにおける設定可能なパラメーターは以下の通り。

Paramater	Range	Default	Description
lr	float >= 0	0.001	Learning rate.
learning_rate_power	float < 0	-0.5	Controls how the learning rate decreases during training. Use zero for a fixed learning rate.
initial_accumulator_value	float > 0	0.1	The starting value for accumulators.
l1_regularization_strength	float >= 0	0.0	L1 Regularization Strength.
l2_regularization_strength	float >= 0	0.0	L2 Regularization Strength.
l2_shrinkage_regularization_strength	float >= 0	0.0	This differs from L2 above in that the L2 above is a stabilization penalty, whereas this L2 shrinkage is a magnitude penalty. When input is sparse shrinkage will only happen on the active weights.

Web上にはFTRLの数式を紹介した記事があまりないようなので、元論文に載っている数式(だいぶ簡略化したが恐らく正しいはず)を記しておく。

Algorithm 1:Per-Coordinate FTRL-Proximal with L1 and L2 Regularization for Logistic Regression

\begin{align}
  & \sigma = \frac{1}{\alpha}(\sqrt{n_{t} + g_{t}^{2}} - \sqrt{n_{t}}) \\
  & z_{t+1} = z_{t} + g_{t} - \sigma w_{t} \\
  & n_{t+1} = n_{t} + g_{t}^{2} \\
  & w_{t+1} = \left\{
    \begin{array}{ll}
      - ( \frac{\beta+\sqrt{n_{t+1}}}{\alpha} + \lambda_{2})^{-1}(z_{t+1} - \textrm{sgn}(z_{t+1}) \lambda_{1})  & (\textrm{if } |z_{t+1}| > \lambda_{1} ) \\
      0 & ( \textrm{otherwise.})
    \end{array}
  \right. \\
\end{align}

なぜこれで学習ができるのかはよくわからない。
TensorFlow内ではおおむね以下のような処理になっているようだ。

ftrl.py

lr_pow = -self.lr_power 
nn = self.n + (grad**2)
sigma = ((nn**lr_pow ) - (self.n**lr_pow )) / lr 
z = self.z + grad - (sigma * var);
if abs(z)>l1:
  x = z - (l1 * sign(z));
  y = ((nn**lr_pow )/lr) + (2*l2)
  var = -x / y
else:
  var = 0
self.n = nn
self.z = z

元論文と若干違いがあるのが気になるが、lr_power=-0.5の場合は大体同じ結果になるはずだ。
数式中の$\alpha$がlrとなり学習率である。$\beta$は無視されている。
varが更新すべき重みで、これまで実験してきた他のアルゴリズムでは、「gradから、次のvarへの差分」を計算していたが、ここでは「gradとvarから、次のvarそのもの」を計算するかたちとなっている。
また、l1が設定されている場合は、条件によって重みが直接0になる場合が出てくる。ニューラルネットをスパース化させることが目的のようだ。
TensorFlowのコードを見ると、l2_shrinkage_regularization_strength を使う場合は少し違うアルゴリズムになるようだが、処理の内容は記載しない。

以下、lrの設定実験。

以下、lr_powerの設定実験。

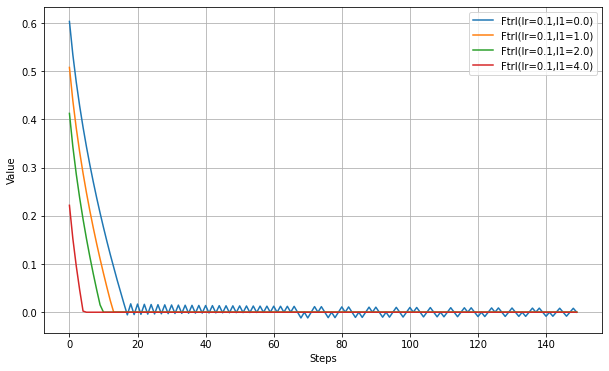
以下、l1_regularization_strengthの設定実験。

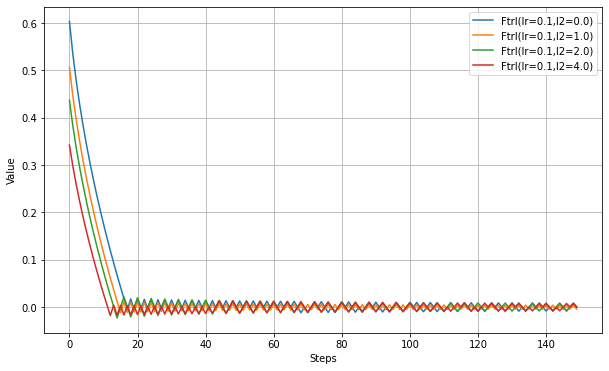
以下、l2_regularization_strengthの設定実験。

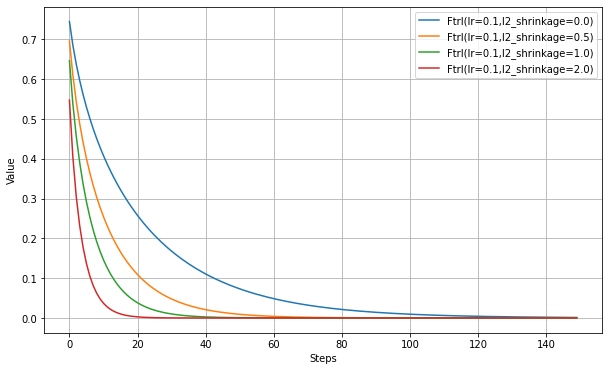
以下、l2_shrinkage_regularization_strengthの設定実験。

まとめ

特定の用途で使われるようだが、Web上の情報が他のアルゴリズムより少なく、結局どういうものかよくわからない。
実験結果は他のアルゴリズムと大差ないように見える。しかし、(ここには記載しないが)損失関数を少し変えると学習が進まなかったりしたので、使いどころが難しいという印象を持った。

実験コード

TestOptimizer.py

import numpy as np
import tensorflow as tf
import matplotlib.pyplot as plt

from tensorflow.keras.optimizers import SGD,RMSprop,Adagrad,Adadelta,Adam,Nadam,Adamax,Ftrl


def testOptims(optims, lossFn='mae', total_steps=150):
    fig = plt.figure(figsize=(10,6),facecolor="white",)
    ax = fig.add_subplot(111)

    steps = range(total_steps)
    y = np.zeros(total_steps)
    if lossFn=='mae':
        loss = lambda: tf.abs(var1)
    elif lossFn=='mse':
        loss = lambda: var1**2
    elif lossFn=='special':
        loss = lambda: var1*(1010 if (i % 101) == 1 else -10)

    for label, optim in optims.items():
        var1 = tf.Variable(1.0)
        for i in range(total_steps):
            optim.minimize(loss, [var1]).numpy()
            y[i] = var1.numpy()
        ax.plot( steps, y, label=label )

    ax.legend(bbox_to_anchor=(1.0,1.0))        
    ax.set_xlabel('Steps')
    ax.set_ylabel('Value')
    ax.grid()
    plt.show()
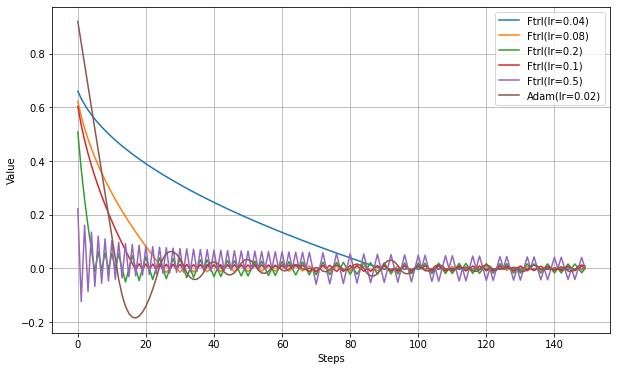
print('Ftrl(lr,mae)')
testOptims(
    {
        'Ftrl(lr=0.04)': Ftrl(0.04),
        'Ftrl(lr=0.08)': Ftrl(0.08),
        'Ftrl(lr=0.2)': Ftrl(0.2),
        'Ftrl(lr=0.1)': Ftrl(0.1),
        'Ftrl(lr=0.5)': Ftrl(0.5),
        'Adam(lr=0.02)': Adam(0.08),
    },
    lossFn = 'mae' 
)
print('Ftrl(lr,mse)')
testOptims(
    {
        'Ftrl(lr=0.04)': Ftrl(0.04),
        'Ftrl(lr=0.08)': Ftrl(0.08),
        'Ftrl(lr=0.2)': Ftrl(0.2),
        'Ftrl(lr=0.1)': Ftrl(0.1),
        'Ftrl(lr=0.5)': Ftrl(0.5),
        'Adam(lr=0.02)': Adam(0.08),
    },
    lossFn = 'mse' 
)
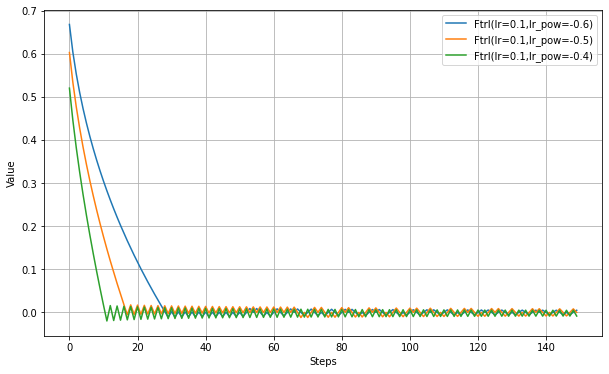
print('Ftrl(learning_rate_power)')
testOptims(
    {
        'Ftrl(lr=0.1,lr_pow=-0.6)': Ftrl(0.1, learning_rate_power=-0.6),
        'Ftrl(lr=0.1,lr_pow=-0.5)': Ftrl(0.1, learning_rate_power=-0.5),
        'Ftrl(lr=0.1,lr_pow=-0.4)': Ftrl(0.1, learning_rate_power=-0.4),
    },
    lossFn = 'mae' 
)

print('FTRL(l1_regularization_strength)')
testOptims(
    {
        'Ftrl(lr=0.1,l1=0.0)': Ftrl(0.1, l1_regularization_strength=0.0),
        'Ftrl(lr=0.1,l1=1.0)': Ftrl(0.1, l1_regularization_strength=1.0),
        'Ftrl(lr=0.1,l1=2.0)': Ftrl(0.1, l1_regularization_strength=2.0),
        'Ftrl(lr=0.1,l1=4.0)': Ftrl(0.1, l1_regularization_strength=4.0),
    },
    lossFn = 'mae' 
)
print('FTRL(l2_regularization_strength)')
testOptims(
    {
        'Ftrl(lr=0.1,l2=0.0)': Ftrl(0.1, l2_regularization_strength=0.0),
        'Ftrl(lr=0.1,l2=1.0)': Ftrl(0.1, l2_regularization_strength=1.0),
        'Ftrl(lr=0.1,l2=2.0)': Ftrl(0.1, l2_regularization_strength=2.0),
        'Ftrl(lr=0.1,l2=4.0)': Ftrl(0.1, l2_regularization_strength=4.0),
    },
    lossFn = 'mae' 
)
print('FTRL(l2_shrinkage)')
testOptims(
    {
        'Ftrl(lr=0.1,l2_shrinkage=0.0)': Ftrl(0.1, l2_shrinkage_regularization_strength=0.0),
        'Ftrl(lr=0.1,l2_shrinkage=0.5)': Ftrl(0.1, l2_shrinkage_regularization_strength=0.5),
        'Ftrl(lr=0.1,l2_shrinkage=1.0)': Ftrl(0.1, l2_shrinkage_regularization_strength=1.0),
        'Ftrl(lr=0.1,l2_shrinkage=2.0)': Ftrl(0.1, l2_shrinkage_regularization_strength=2.0),
    },
    lossFn = 'mse' 
)