最適化アルゴリズムを単独実行で比較する(SGD編)

はじめに

この記事では、数式は使わず、実際のコードから翻訳した疑似コードを使って動作を紹介する。また、Keras(Tensorflow)のOptimizerを単独実行させた実験結果を示すことにより、各種最適化アルゴリズムでのパラメーターの効果や、アルゴリズム間の比較を行う。

Adagrad/RMSprop/Adadelta編
Adam/Adamax/Nadam編
FTRL編
総合編

実験方法

極簡単なネットワークを学習させ、学習過程をグラフにプロットして比較する。
具体的には、下記の内容。

• 初期値1.0、最適値0.0として、Optimiserのminimize()を直接実行し、ステップ毎に最適値に近づく様子を観察する。
• 損失関数は特に言及しない限り絶対値(MAE)を使用。場合によっては二乗(MSE)なども使用。
• Keras使用。Google Colabで実行可な実験コードを最後に記載。

SGD

最も基本的なOptimizer。TensorFlowではパラメータの設定によってVanillaSGD/MomentumSGD/NAGと別々にも呼ばれるアルゴリズムになるがコードは共通。

下記のコードでKerasでの実装がわかる。
keras/optimizers.py
gradient_descent.py
TensorFlow Document

設定可能なパラメーターは以下の通り。

Parameter	Range	Default	Description
learning_rate	float >= 0	0.01	The learning rate.
momentum	float >= 0	0	Hyperparameter that accelerates gradient descent in the relevant direction and dampens oscillations.
nesterov	boolean	False	Whether to apply Nesterov momentum.

またKeras/TensorFlowのOptimiser共通で下記のパラメータも使用できる。

Parameter	Range	Default	Description
decay	float >= 0	0	Learning rate decay over each update.
clipvalue	float >= 0	None	the gradient of each weight is clipped to be no higher than this value.
clipnorm	float >= 0	None	the gradient of each weight is individually clipped so that its norm is no higher than this value.
global_clipnorm	float >= 0	None	the gradient of all weights is clipped so that their global norm is no higher than this value.

内部処理を翻訳すると以下のようなコードになっている。

def get_step(grad):
  v = (self.momentum * self.v_prev) - (lr * grad)
  self.v_prev = v     
  if self.nesterov:
    v = (self.momentum * v) - (lr * grad)
  return v

以下、各パラメータがどのように機能するか、実際の動作で確認する。

Vanilla SGD

デフォルトでは、慣性項なしのSGDとなる。区別のため'Vanilla SGD'と呼ばれる場合もある。勾配に学習率を掛けた値だけで更新幅が決まる。

Learning Rate(学習率)の数値だけ変更して実験。

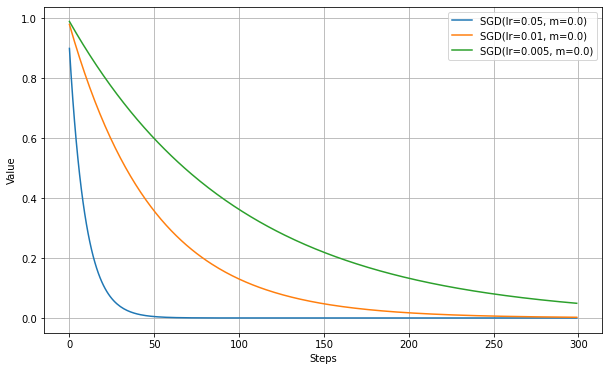
学習率を大きくすると、最適値に到達するステップ数が短くなる。
しかし、学習率が大きくなるに従い、最適値付近の振動が激しくなる。
実験では損失関数がMAEであるため、直線的に学習が進む。

Momentum SGD

momentumを0以上にすると、慣性項が追加される。これにより、以下のような効果が期待される。

• 学習の加速(同一方向の勾配は強化されるため)
• 振動の抑制(細かな変動は反映されにくくなるため)

これはVanilla SGDと区別してMomentum SGDと呼ばれることもある。SGDとだけ表記してある場合、どちらの可能性もあるので少し注意が必要。

以下は、momentum=0.7として、最初の実験と同じ学習率で実験した結果。

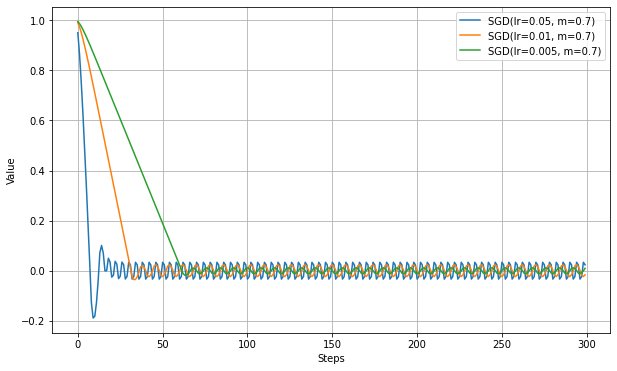
VanillaSGDの実験結果と比べて、最適値に到達するまでのステップ数が短縮されている。ただし、振動の細かさは軽減されるが、振幅は逆に増加しているように見える。
Momentumで学習が速くなったようにみえるが、VanillaSGDとは学習率の解釈がすこし違うので、ここは同じ学習率で比べるのはあまり意味がないかもしれない。

以下は、lr固定でmomentumの数値を変更した結果。

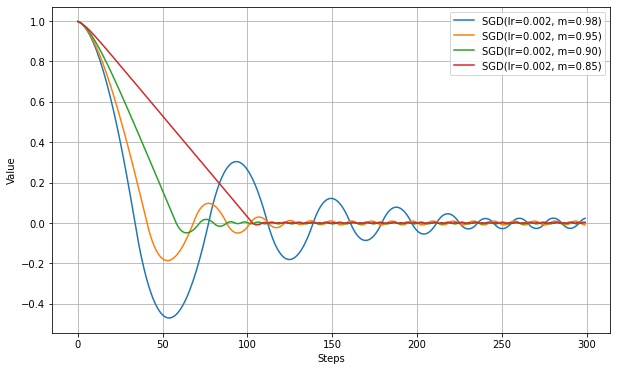
momentumの数値が大きくなるにつれて加速が強まり、最適値に到達するまでのステップが短縮される。
ただし、大きくしすぎると最適値付近で振動が大きくなり、収束までは時間がかかる。

NAG

nesterovをTrueとすると、Nesterovの加速法（Nesterov's Accelerated Gradient Method）が適用される。これはNAGと表記されることがある。
一つ先のイテレーションでの計算を先読み（推測）して織り込むことで、加速や振動抑制効果が上がることが期待される模様。Kerasの実装を見る限り、まずMomentumSGDと同じ計算で変更量を計算した後、次回でも同じ勾配であることを仮定することにより次回分のMomentumSGDの計算を行い、それを使って最終的な変更量を決定するようだ。仮定が入るので、ここは推定量となる。

以下は、MomentumSGDの実験と同じ設定で、nesterovをTrueにした結果。

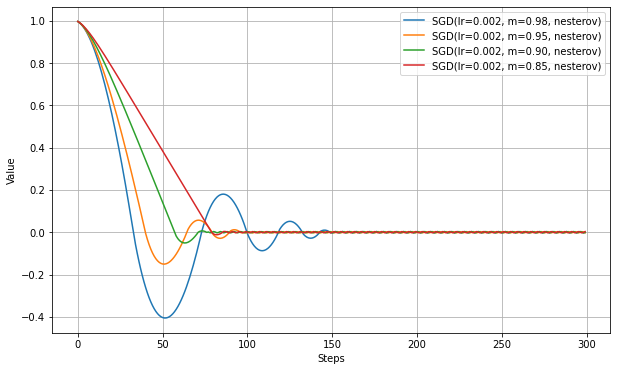
比較すると、振動が抑制されていることがわかる。
最適値に到達するステップ数も若干短縮されているが、大きな違いはみられない。これは慣性項自体の更新は通常のMomentumSGDと同じため、加速の程度に大きな違いがないためと思われる。

Decayの効果

decayを0以上にすると、1ステップごとに学習率が減少していくようになる。これにより、学習の終盤で振動が抑制されることが期待される。

コードにすると下記の通り。

  lr = self.lr * (1. / (1. + self.decay*iterations))

以下は、大きく振動する設定において、Decayの効果を確認する実験。

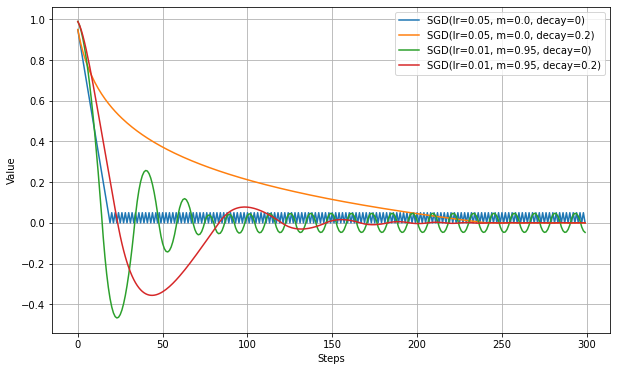
decayにより振動が減っていることがわかる。ただし、最適値への到達ステップ数は増える。
学習率が徐々に低くなるので当然の結果ではある。

Clipの効果

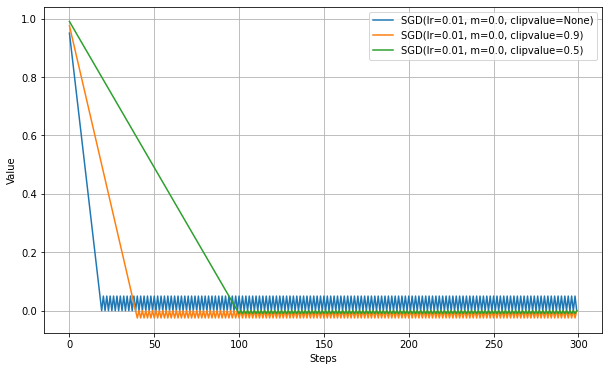
勾配の大きさに制限を加えると学習結果が良い場合に設定する。
ここではclipvalueについてのみ実験。

損失関数はMAEである関係で、Clipを設けない場合は勾配は常に1.0になる。1.0以下のclipvalueによって勾配が制限され、学習が遅くなっていることがわかる。

損失関数の影響

これまでの実験はすべて損失関数はMAEで実施した。
損失関数をMSEで行った実験も記載しておく。

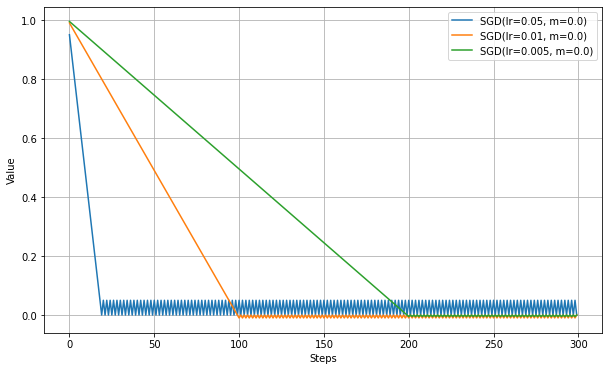
以下、VanillaSGDの最初の実験と同じ設定で、損失関数をMSEにした場合の結果。

学習が曲線的になり、細かい振動が見られない。また、この実験条件ではMAEのほうが早く最適値に到達する。
なぜこのような違いが出るかは、Hatomugi氏の下記の記事など参照のこと。
損失関数のまとめ (Huber,Log-Cosh,Poisson,CustomLoss,MAE,MSE)

まとめ

• Momentumは、学習の加速に対して貢献が大きいが、振動の振幅が大きくなる場合がある。
• Nesterovは、振動抑制効果があり、加速効果も若干ある。
• Decayは、学習が進むにつれて振動が抑制されるが、学習が遅くなる。

#参考

深層学習の最適化アルゴリズム
勾配降下法一覧 (2020)
【2020決定版】スーパーわかりやすい最適化アルゴリズム -損失関数からAdamとニュートン法-※

※こちらの記事では、元の数式が違うので慣性項が指数移動平均として扱われている。本記事に記したような実装が一般的なようであるが、学習率の解釈が違うだけで本質的には同じもの。

実験コード

TestOptimizerSGD.py

import numpy as np
import tensorflow as tf
import matplotlib.pyplot as plt

from tensorflow.keras.optimizers import SGD,RMSprop,Adagrad,Adadelta,Adam


def testOptims(optims, lossFn='mae', total_steps=120):
    fig = plt.figure(figsize=(10,6),facecolor="white",)
    ax = fig.add_subplot(111)

    steps = range(total_steps)
    y = np.zeros(total_steps)
    if lossFn=='mae':
        loss = lambda: tf.abs(var1)
    elif lossFn=='mse':
        loss = lambda: var1**2

    for label, optim in optims.items():
        var1 = tf.Variable(1.0)
        for i in range(total_steps):
            optim.minimize(loss, [var1]).numpy()
            y[i] = var1.numpy()
        ax.plot( steps, y, label=label )
    
    ax.legend(bbox_to_anchor=(1.0,1.0))        
    ax.set_xlabel('Steps')
    ax.set_ylabel('Value')
    ax.grid()
    plt.show()

print( 'VanillaSGD')
testOptims(
    {
        'SGD(lr=0.05, m=0.0)' : SGD(lr=0.05,  momentum=0.0 ),
        'SGD(lr=0.01, m=0.0)' : SGD(lr=0.01,  momentum=0.0 ),
        'SGD(lr=0.005, m=0.0)': SGD(lr=0.005, momentum=0.0 ),
    },
    total_steps=300
)

print( 'MomentumSGD(1)')
testOptims(
    {
        'SGD(lr=0.05, m=0.7)'  : SGD(lr=0.05,  momentum=0.7 ),
        'SGD(lr=0.01, m=0.7)'  : SGD(lr=0.01,  momentum=0.7 ),
        'SGD(lr=0.005, m=0.7)' : SGD(lr=0.005, momentum=0.7 ),
    },
    total_steps=300
)
print( 'MomentumSGD(2)')
testOptims( 
    {
        'SGD(lr=0.002, m=0.98)' : SGD(lr=0.002, momentum=0.98 ),
        'SGD(lr=0.002, m=0.95)' : SGD(lr=0.002, momentum=0.95 ),
        'SGD(lr=0.002, m=0.90)' : SGD(lr=0.002, momentum=0.9 ),
        'SGD(lr=0.002, m=0.85)' : SGD(lr=0.002, momentum=0.8 ),
    },
    total_steps=300
)
print( 'NAG')
testOptims( 
    {
        'SGD(lr=0.002, m=0.98, nesterov)' : SGD(lr=0.002, momentum=0.98, nesterov=True ),
        'SGD(lr=0.002, m=0.95, nesterov)' : SGD(lr=0.002, momentum=0.95, nesterov=True ),
        'SGD(lr=0.002, m=0.90, nesterov)' : SGD(lr=0.002, momentum=0.90, nesterov=True ),
        'SGD(lr=0.002, m=0.85, nesterov)' : SGD(lr=0.002, momentum=0.85, nesterov=True ),
    },
    total_steps=300
)
print( 'SGD(decay)')
testOptims( 
    {
        'SGD(lr=0.05, m=0.0,  decay=0)'  : SGD(lr=0.05, momentum=0.0,  decay=0),
        'SGD(lr=0.05, m=0.0,  decay=0.2)': SGD(lr=0.05, momentum=0.0,  decay=0.2),
        'SGD(lr=0.01, m=0.95, decay=0)'  : SGD(lr=0.01, momentum=0.95, decay=0),
        'SGD(lr=0.01, m=0.95, decay=0.2)': SGD(lr=0.01, momentum=0.95, decay=0.2),
    },
    total_steps=300
)
print( 'SGD(clipvalue)')
testOptims( 
    {
        'SGD(lr=0.05, m=0.0, clipvalue=None)': SGD(lr=0.05, momentum=0.0, clipvalue=None),
        'SGD(lr=0.05, m=0.0, clipvalue=0.9)' : SGD(lr=0.05, momentum=0.0, clipvalue=0.5),
        'SGD(lr=0.05, m=0.0, clipvalue=0.5)' : SGD(lr=0.05, momentum=0.0, clipvalue=0.2),
    },
    total_steps=300
)
print('Loss Function = mse')
testOptims(
    {
        'SGD(lr=0.05, m=0.0)' : SGD(lr=0.05,  momentum=0.0 ),
        'SGD(lr=0.01, m=0.0)' : SGD(lr=0.01, momentum=0.0 ),
        'SGD(lr=0.005, m=0.0)': SGD(lr=0.005, momentum=0.0 ),
    },
    total_steps=300,
    lossFn='mse'
)