Go to Qiita Advent Calendar 2024 Top
LoginSignup
5
2

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?

More than 3 years have passed since last update.

@T-STAR

最適化アルゴリズムを単独実行で比較する(Adam/Adamax/Nadam編)

Last updated at Posted at 2020-11-18

はじめに

この記事では、数式は使わず、実際のコードから翻訳した疑似コードを使って動作を紹介する。また、Keras(Tensorflow)のOptimizerを使用した実験結果を示すことにより、各種最適化アルゴリズムでのパラメーターの効果や、アルゴリズム間の比較を行う。

ここでは、Adam/Adamax/Nadamを扱う。
SGD編
Adagrad/RMSprop/Adadelta編
FTRL編
総合編

実験方法

極簡単なネットワークを学習させ、学習過程をグラフにプロットして比較する。
具体的には、下記の内容。

  • 初期値1.0、最適値0.0として、Optimiserのminimize()を直接実行し、ステップ毎に最適値に近づく様子を観察する。
  • 損失関数は特に言及しない限り絶対値(MAE)を使用。場合によっては二乗(MSE)なども使用。
  • Keras使用。Google Colabで実行可な実験コードを最後に記載。

Adam

RMSpropの改良版。最もポピュラーなアルゴリズムの一つ。
RMSpropでは修正学習率に直接勾配を掛けた形になるが、Adamでは勾配も指数移動平均を使う。

Keras実装は以下を参照した。
adam.py
training_ops.cc
TensorFlow API Adam

Adamの論文。
Adam - A Method for Stochastic Optimization

Adamにおける設定可能なパラメーターは以下の通り。

Paramater Range Default Description
lr float >= 0 0.001 Learning rate.
beta_1 float, 0 < beta < 1 0.9 The exponential decay rate for the 1st moment estimates.
beta_2 float, 0 < beta < 1 0.999 The exponential decay rate for the 2nd moment estimates.
amsgrad Boolean False Whether to apply AMSGrad variant of this algorithm from the paper "On the Convergence of Adam and beyond"
epsilon float >= 0 1e-8 A small constant for numerical stability.

内部処理を翻訳すると以下のようなコードになっている。

def get_step(grad):
  self.m =  (self.beta_1 * self.m) + ((1. - self.beta_1) * grad)
  self.v =  (self.beta_2 * self.v) + ((1. - self.beta_2) * (grad**2))
  lr_t = lr * ((1. - (self.beta_2**iterations))**0.5) /
                     (1. - (self.beta_1**iterations))
  if amsgrad:
    self.vhat = max(self.vhat, self.v)
    v = -lr_t * self.m / ( (self.vhat**0.5)+self.epsilon )
  else:
    v = -lr_t * self.m / ( (self.v**0.5)+self.epsilon )
  return v

コード上のlr_tは、本来は不偏推定量をとるために勾配(m)と二乗勾配(v)に掛ける補正係数を、そこだけ抜き出して学習率に掛けたものあり、最終的な結果は同じ。

以下、学習率だけ設定した実験結果。

Adam(lr).png

RMSpropよりも最適解近くでの振動が少ないように見える。

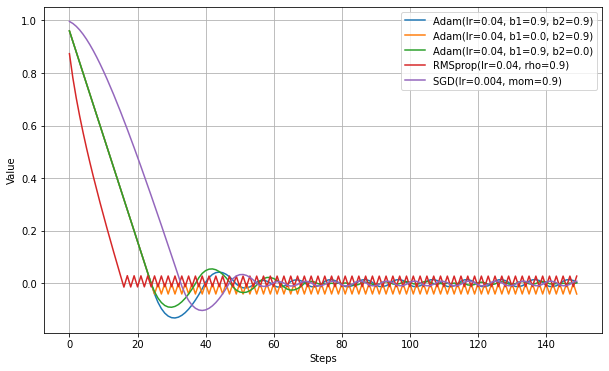
AdamはRMSpropにMomentumを導入したもので、beta_1がMomentumSGDでのmomentum、beta_2がRMSpropでのrhoにあたる。
逆にいうと、beta_1を0にするとRMSprop相当、beta_2を0にするとMomentumSGD相当となる。ただし、Adamでは指数移動平均のバイアスをとる処理が入っている。

以下、beta_1とbeta_2を0にして比較したもの。
adam_comp.png

赤がRMSpropで、オレンジがAdam(beta_1=0)でRMSprop相当。バイアス補正の分若干ずれがあるが、形は似ている。
紫がMomenutumSGDで、緑がAdam(beta2=0)でMomentumSGD相当。学習率の効き方が違うので、できるだけ合わせるためにSGDのほうの学習率を1/10であらかじめ補正した。こちらも形が似ている。

AMSGrad

amsgrad=TrueとするとAMSGradと呼ばれるアルゴリズムになる。過去の勾配の長期記憶を使うことにより、Adamでは収束できないような形の最適解での性能向上できるという。

AMSGradの論文。
ON THE CONVERGENCE OF ADAM AND BEYOND

単純にamsgrad=Trueとしても、これまで使用してきたMAEやMSEの損失関数では通常のAdamとの差は見られなかった。
論文によると、AMSgradは'Adamでは収束できない条件があることへの改良版'ということで、その条件が例示されているので、その条件を再現して実験してみる。

下記のような損失関数を用意してAdamとAMSgradで比較する。

loss = lambda: var1*(1010 if (i % 101) == 1 else -10)

(i%101)==1の条件で(つまり101回に1回)、他とは逆方向の勾配が現れることになる。Adamではこの勾配をすぐ忘れてしまうので収束できない、とされている。

以下、実際にやってみた結果。(lr=0.1/beta_1=0.9/beta_2=0.99)
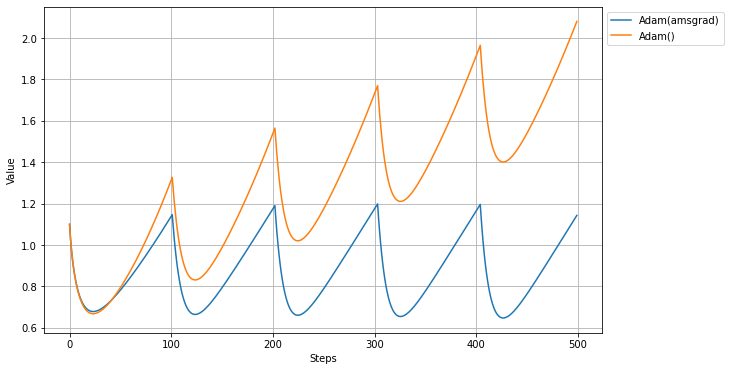
Adam(special).png

この条件では、AdamとAMSgradで大きな違いが出た。
Adamでは値がどんどん大きくなっていくが、AMSGradではほぼ同じ場所にとどまっている。
論文では-1が最適値とされているので、Adamよりは正確な値に近いように見える。

#Adamax

Adamの変形バージョン。
理論はともかく、二乗勾配が消えて勾配絶対値となり、過去の勾配の指数移動平均よりも大きな勾配が来た場合には、保持していた平均をクリアして最新の勾配絶対値に更新されるように見える。

Keras実装は以下を参照した。
adamax.py
TensorFlow API Adamax

Adamの論文に同時記載。
Adam - A Method for Stochastic Optimization

AdaMaxにおける設定可能なパラメーターは以下の通り。

Paramater Range Default Description
lr float >= 0 0.001 Learning rate.
beta_1 float, 0 < beta < 1 0.9 The exponential decay rate for the 1st moment estimates.
beta_2 float, 0 < beta < 1 0.999 The exponential decay rate for the exponentially weighted infinity norm.
epsilon float >= 0 1e-7 A small constant for numerical stability.

以下、処理を翻訳したもの。

def get_step(grad):
  lr = self.lr * (1. / (1. + self.decay * iterations))
  self.m = (self.beta_1 * self.m) + (1. - self.beta_1) * grad
  self.u = max(self.beta_2 * self.u, abs(grad))
  lr_t = lr / (1. - (self.beta_1**t))
  v = -lr_t * self.m / (self.u + self.epsilon)
  return v

以下、学習率だけ設定した実験結果。
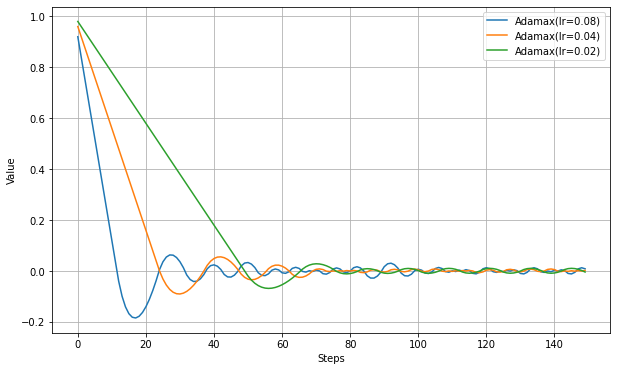
Adamax(lr).png

この実験ではAdamとの違いがよくわからなかった。

#Nadam

AdamにSGDで採用されているNestrov加速法を適用したもの。

Keras実装は以下を参照した。
nadam.py
TensorFlow API Nadam

Nadamの論文
Nadam report

Nadamにおける設定可能なパラメーターは以下の通り。

Paramater Range Default Description
lr float >= 0 0.001 Learning rate.
beta_1 float, 0 < beta < 1 0.9 The exponential decay rate for the 1st moment estimates.
beta_2 float, 0 < beta < 1 0.999 The exponential decay rate for the exponentially weighted infinity norm.
epsilon float >= 0 1e-7 A small constant for numerical stability.

以下、処理を翻訳したもの。

def get_step(grad):
　t = iteration+1
  momentum_cache_t = self.beta_1 * (1. - 0.5 * (pow(0.96, t * self.schedule_decay)))
  momentum_cache_t_1 = self.beta_1 * (1. - 0.5 * (pow(0.96, (t + 1) * self.schedule_decay)))
  m_schedule_new = self.m_schedule * momentum_cache_t
  m_schedule_next = m_schedule_new * momentum_cache_t_1
  m_t = self.beta_1 * self.m + (1. - self.beta_1) * grad
  v_t = self.beta_2 * self.v + (1. - self.beta_2) * (g**2)
  g_prime = grad / (1. - m_schedule_new)
  m_t_prime = m_t / (1. - m_schedule_next)
  v_t_prime = v_t / (1. - (self.beta_2**t))
  self.v = v_t
  self.m = m_t
  m_t_bar = (1. - momentum_cache_t) * g_prime + momentum_cache_t_1 * m_t_prime
  v = - self.lr * m_t_bar / ((v_t_prime**0.5) + self.epsilon)  
  return v

コードを見ただけではなにをやっているかよくわからないが、元論文にどうしてこうなるか書いてある模様。

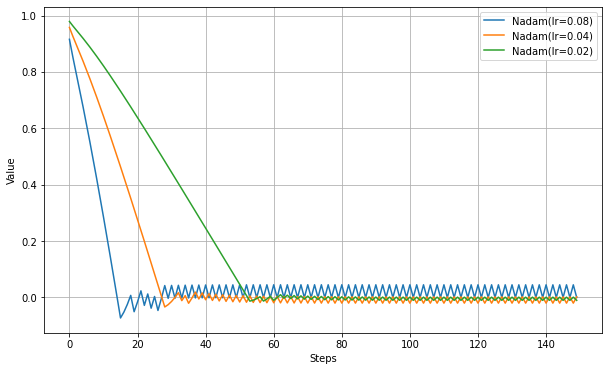
以下、学習率だけ設定した実験結果。

Nadam(lr).png

Adamに比べて最適値辺りのふるまいが大きく違う。NAGで見られたように振動抑制の効果が強いようだ。

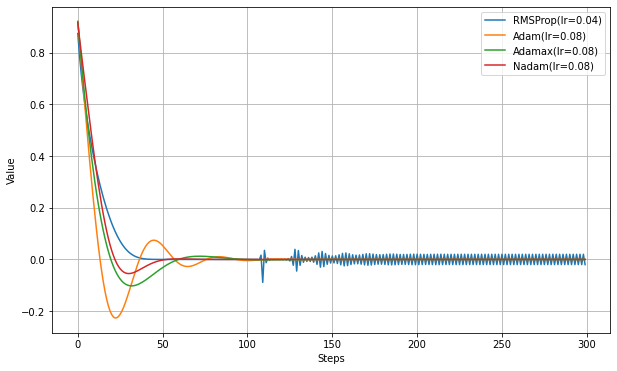
RMSpropでは勾配が0に近くなると不安定にある現象が見られるので、Adam/Adamax/NadamでもMSEにして比較実験する。

Adam(MSE).png

RMSpropのように不安定になることは無いようだ。
MAEではAdamaxとAdamの違いがあまりなかったが、MSEにするとはっきりした違いが出る。

#まとめ

  • AdamはRMSpropと比較すると最適値付近できれいに収束するように見える。学習率を変化させても収束しやすいようで、この辺も人気の理由か。
  • AMSgradはAdamの改良版だが、かなり特殊な勾配にしないと違いがはっきり表れなかった。
  • AdamaxはAdamの派生版だが、Adamよりは最適値に向かう速度は若干遅いが、最適値付近での振動が穏やかになっているように見える。
  • NadamはAdamにNesterovを適用したもので、Adamよりも最適値へ向かう速度は若干遅いが、最適値付近での振幅が少なくなっているように見える。ただし、MAEでは細かい振動が収まらない。

複雑な条件での比較は別記事で行うことにする。

#参考

深層学習の最適化アルゴリズム
勾配降下法一覧 (2020)

実験コード
TestOptimizer.py
import numpy as np
import tensorflow as tf
import matplotlib.pyplot as plt

from tensorflow.keras.optimizers import SGD,RMSprop,Adagrad,Adadelta,Adam,Nadam,Adamax,Ftrl


def testOptims(optims, lossFn='mae', total_steps=150):
    fig = plt.figure(figsize=(10,6),facecolor="white",)
    ax = fig.add_subplot(111)

    steps = range(total_steps)
    y = np.zeros(total_steps)
    if lossFn=='mae':
        loss = lambda: tf.abs(var1)
    elif lossFn=='mse':
        loss = lambda: var1**2
    elif lossFn=='special':
        loss = lambda: var1*(1010 if (i % 101) == 1 else -10)

    for label, optim in optims.items():
        var1 = tf.Variable(1.0)
        for i in range(total_steps):
            optim.minimize(loss, [var1]).numpy()
            y[i] = var1.numpy()
        ax.plot( steps, y, label=label )
    
    ax.legend(bbox_to_anchor=(1.0,1.0))        
    ax.set_xlabel('Steps')
    ax.set_ylabel('Value')
    ax.grid()
    plt.show()

print('Adam(lr)')
testOptims(
    {
        'Adam(lr=0.08)': Adam(0.08),
        'Adam(lr=0.04)': Adam(0.04),
        'Adam(lr=0.02)': Adam(0.02),
    },
    lossFn = 'mae' 
)
print('Adam/RMSprop/SGD')
testOptims(
    {
        'Adam(lr=0.04, b1=0.9, b2=0.9)': Adam(0.04, beta_1=0.9, beta_2=0.9),
        'Adam(lr=0.04, b1=0.0, b2=0.9)': Adam(0.04, beta_1=0.0, beta_2=0.9),
        'Adam(lr=0.02, b1=0.9, b2=0.0)': Adam(0.04, beta_1=0.9, beta_2=0.0),
        'RMSprop(lr=0.04, rho=0.9)': RMSprop(0.04, rho=0.9),
        'SGD(lr=0.004, mom=0.9)':    SGD(0.004, momentum=0.9),  
    },
    lossFn = 'mae' 
)

print('Adam(beta_1)')
testOptims(
    {
        'Adam(lr=0.08, beta_1=0.999)': Adam(0.08, beta_1=0.999),
        'Adam(lr=0.08, beta_1=0.95)': Adam(0.08, beta_1=0.95),
        'Adam(lr=0.08, beta_1=0.90)': Adam(0.08, beta_1=0.90),
        'Adam(lr=0.08, beta_1=0.85)': Adam(0.08, beta_1=0.85),
    },
    lossFn = 'mae' 
)
print('Adam(beta_2,mae)')
testOptims(
    {
        'Adam(lr=0.08, beta_2=0.999)': Adam(0.08, beta_2=0.999),
        'Adam(lr=0.08, beta_2=0.95)': Adam(0.08, beta_2=0.95),
        'Adam(lr=0.08, beta_2=0.90)': Adam(0.08, beta_2=0.90),
        'Adam(lr=0.08, beta_2=0.85)': Adam(0.08, beta_2=0.85),
    },
    lossFn = 'mae' 
)
print('Adam(beta_2,mse)')
testOptims(
    {
        'Adam(lr=0.08, beta_2=0.999)': Adam(0.08, beta_2=0.999),
        'Adam(lr=0.08, beta_2=0.95)': Adam(0.08, beta_2=0.95),
        'Adam(lr=0.08, beta_2=0.90)': Adam(0.08, beta_2=0.90),
        'Adam(lr=0.08, beta_2=0.85)': Adam(0.08, beta_2=0.85),
    },
    lossFn = 'mse' 
)
print('AMSGrad(mse)')
testOptims(
    {
        'Adam(lr=0.08)': Adam(0.08),
        'Adam(lr=0.08,amsgrad)': Adam(0.08,amsgrad=True),
    },
    lossFn = 'mse' 
)
print('AMSgrad(special)')
testOptims(
    {
        'Adam(amsgrad)': Adam(0.1, beta_1=0.9, beta_2=0.99, amsgrad=True),
        'Adam()'       : Adam(0.1, beta_1=0.9, beta_2=0.99, amsgrad=False),
    },
    lossFn='special',
    total_steps=500
)


print('Adam vs RMSprop(mom)')
testOptims(
    {
        'Adam(lr=0.08)': Adam(0.08),
        'RMSProp(lr=0.01, momentum=0.9)': RMSprop(0.01, momentum=0.9),
    },
    lossFn = 'mae' 
)
print('Adamax(lr)')
testOptims(
    {
        'Adamax(lr=0.08)': Adamax(0.08),
        'Adamax(lr=0.04)': Adamax(0.04),
        'Adamax(lr=0.02)': Adamax(0.02),
    },
    lossFn = 'mae' 
)
print('Nadam(lr)')
testOptims(
    {
        'Nadam(lr=0.08)': Nadam(0.08),
        'Nadam(lr=0.04)': Nadam(0.04),
        'Nadam(lr=0.02)': Nadam(0.02),
    },
    lossFn = 'mae' 
)
print('MSE')
testOptims(
    {
        'RMSProp(lr=0.04)': RMSprop(0.04),
        'Adam(lr=0.08)': Adam(0.08),
        'Adamax(lr=0.08)': Adamax(0.08),
        'Nadam(lr=0.08)': Nadam(0.08),
    },
    lossFn = 'mse' ,
    total_steps=300

)
5
2
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
5
2

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?