ラビットチャレンジの提出レポートです。
##<科目一覧>
深層学習：Day1 (NN)
深層学習：Day2 (CNN)
深層学習：Day3 (RNN)
深層学習：Day4 (Tensorflow & 強化学習)
##Section 1：TensorFlowの実装演習
###1-1) TensorFlowの実装演習
####【実装のソースコード理解】
【定数を定義する】
tf.constant(value, dtype=None, shape=None, name=’Const’, verify_shape=False)
【プレースホルダー】
プレースホルダーはデータが格納される入れ物。データは未定のままグラフを構築し、具体的な値は実行する時に与える。
tf.placeholder(dtype,shape=None,name=None)
【変数定義】
tf.Variable()
【値の更新】
tf.assign(
ref,
value,
validate_shape=None,
use_locking=None,
name=None
)
【平均値】
tf.math.reduce_mean(
input_tensor,
axis=None,
keepdims=False,
name=None
)
【Optimizer】
tf.train.GradientDescentOptimizer
__init__( learning_rate, use_locking=False, name='GradientDescent' )
tf.train.MomentumOptimizer
__init__( learning_rate, momentum, use_locking=False, name='Momentum', use_nesterov=False )
tf.train.AdagradOptimizer
__init__( learning_rate, initial_accumulator_value=0.1, use_locking=False, name='Adagrad' )
tf.train.RMSPropOptimizer
__init__( learning_rate, decay=0.9, momentum=0.0, epsilon=1e-10, use_locking=False, centered=False, name='RMSProp' )
tf.train.AdamOptimizer
__init__( learning_rate=0.001, beta1=0.9, beta2=0.999, epsilon=1e-08, use_locking=False, name='Adam' )
【Dropout】
tf.nn.dropout(
x,
rate,
noise_shape=None,
seed=None,
name=None
)
####【実装演習の結果】
https://github.com/HienDT27/Rabbit-Challenge/blob/master/%E3%80%90%E6%B7%B1%E5%B1%A4%E5%AD%A6%E7%BF%92_Day_04%E3%80%914_1_tensorflow_codes.ipynb
####【実装演習の考察】
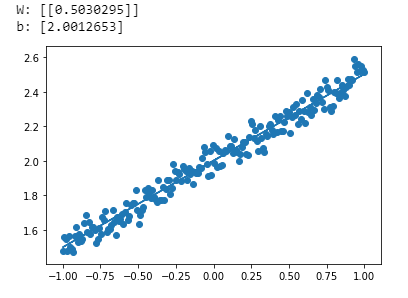
#####① 線形回帰
■ $d = 3x + 2$ の関数で、ノイズの値を変更すると、以下の結果になる。
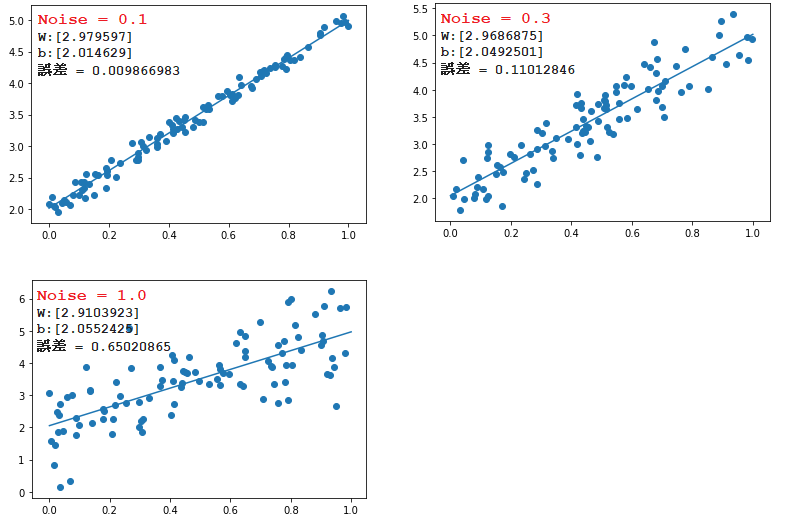
➡ ノイズの値が大きいほど、誤差が大きくなり、予測精度が下がる傾向になります。
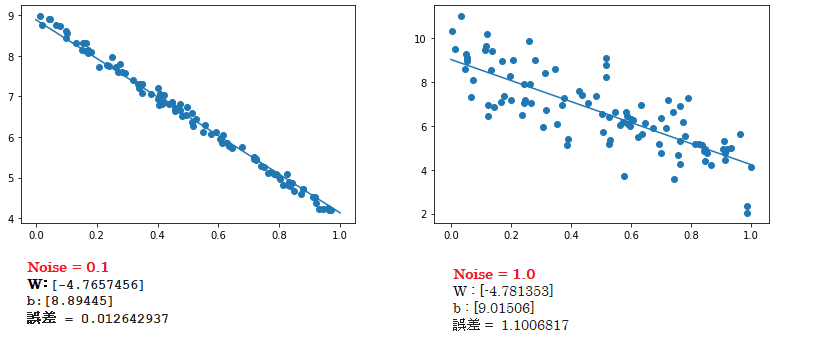
■ 関数 $d$ を $d =-5x + 9$ に変更してみると、上の結果と同じく、Noise の値が小さいほど、回帰式で上手く予測できていることが分かった。
#####➁ 非線形回帰
■ $d = -0.4x^3 + 1.6x^2 -2.8x + 1$ の関数で、ノイズの値を変更すると、以下の結果になる。
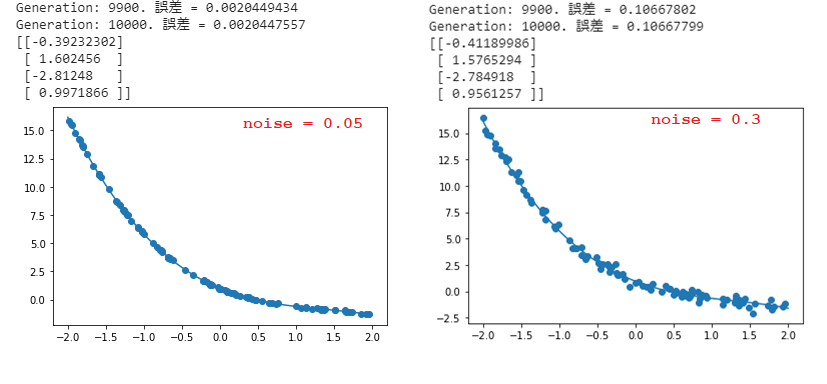
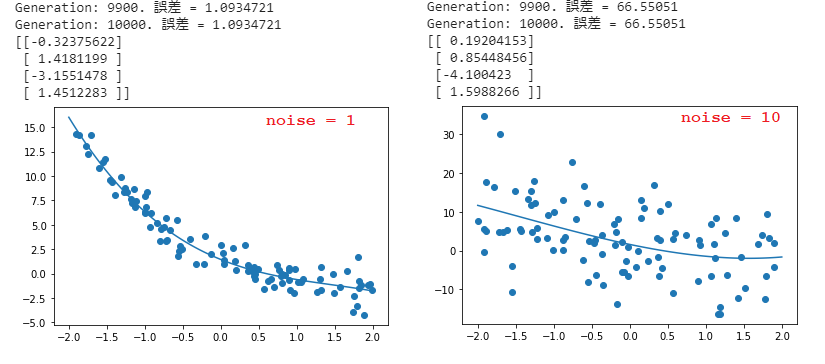
➡ ノイズの値が大きいほど、誤差が大きくなり、予測精度が下がる。
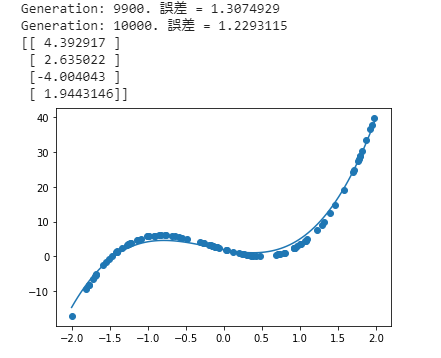
■ $Noise = 0.05$で、関数 $d$ を $d = 5.3x^3 + 2.5x^2 -6.5x + 2$ に変更してみると、
Tensorflowの非線形回帰を使うと、上手く予測できていることが分かる。
#####③ 【Try】
- 次の式をモデルとして回帰を行おう
$$ y=30x^{2} +0.5x+0.2 $$ - 誤差が収束するようiters_numやlearning_rateを調整しよう
【考察】
■ 最初に、(iters_num = 40000, learning_rate = 0.01) では、Generation が16000 ~ 19000の間に一番小さいな誤差が得られる
Generation: 14000. 誤差 = 1.131915e-10
Generation: 15000. 誤差 = 4.1836545e-11
Generation: 16000. 誤差 = 1.6934643e-11
Generation: 17000. 誤差 = 8.383314e-12
Generation: 18000. 誤差 = 7.515821e-12
Generation: 19000. 誤差 = 1.2134322e-11
Generation: 20000. 誤差 = 1.8450566e-11
Generation: 21000. 誤差 = 5.595812e-08
➡ learning_rate = 0.01を設定する場合では、iters_num = 20000で設定すれば、良いの重み結果を得られる（長く学習するのは必要がないです）
■ また、(iters_num = 40000, learning_rate = 0.1) では、Generation が7000 ~ 12000の間に一番小さいな誤差が得られる
Generation: 7000. 誤差 = 3.809217e-11
Generation: 8000. 誤差 = 1.8841257e-11
Generation: 9000. 誤差 = 1.0834719e-11
Generation: 10000. 誤差 = 1.0799477e-11
Generation: 11000. 誤差 = 7.295187e-12
Generation: 12000. 誤差 = 1.2004096e-11
Generation: 13000. 誤差 = 2.5837787e-07
➡ learning_rate = 0.1を設定する場合では、誤差が早めに収束するように見えた。
#####④ 分類１層 (mnist)
■ x：入力値, d：教師データ, W：重み, b：バイアス をそれぞれ定義しよう
x = tf.placeholder(tf.float32, [None, 784])
d = tf.placeholder(tf.float32, [None, 10])
W = tf.Variable(tf.random_normal([784, 10], stddev=0.01))
b = tf.Variable(tf.zeros([10]))
y = tf.nn.softmax(tf.matmul(x, W) + b)
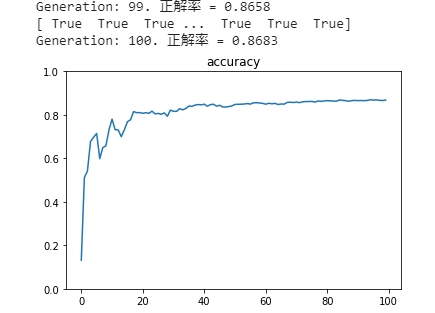
■ 隠れ層を持っていないネットワークでは、分類正答率が86.7％までできる。
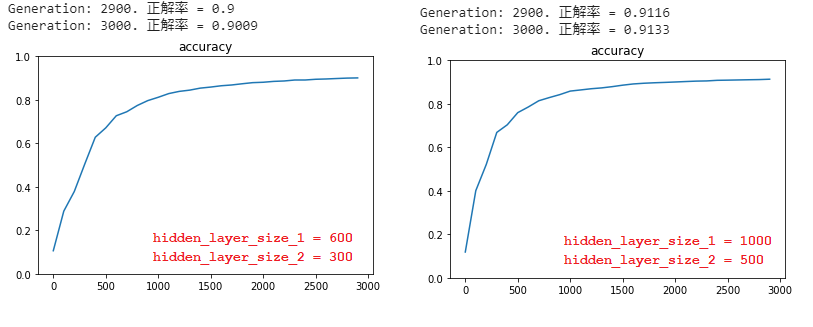
#####⑤ 分類３層 (mnist)
■ 隠れ層のそれぞれのサイズを大きくすると、正答率が上がることが分かった。
■ また、Optimizer方法を変更してみると、以下の結果が得られる。
| optimizer方法 | 正答率 |
|---|---|
| tf.train.GradientDescentOptimizer(0.5) | 0.9169 |
| tf.train.MomentumOptimizer(0.1, 0.9) | 0.943 |
| tf.train.AdagradOptimizer(0.1) | 0.8943 |
| tf.train.RMSPropOptimizer(0.001) | 0.9662 |
| tf.train.AdamOptimizer(1e-4) | 0.9032 |
| ➡ RMSProp方法では一番良い正答率が得られた。 | |
| #####⑥ 分類CNN (mnist) | |
| ■ ドロップアウトを行った (dropout_rate = 0.5) の場合では、正答率 0.96であり、ドロップアウトを行わなかった場合の正答率が 0.98 という結果で、ドロップアウトを行わなかったほうが正答率が高くなった。 | |
| ##1-2) Keras の実装演習 | |
| ####【実装のソースコード理解】 | |
| 【データを訓練用とテスト用に分割する】 |
sklearn.model_selection.train_test_split(*arrays, **options)
【optimizers】
・SGDの場合：
keras.optimizers.SGD(learning_rate=0.01, momentum=0.0, nesterov=False)
・RMSpropの場合：
keras.optimizers.RMSprop(learning_rate=0.001, rho=0.9)
・Adagradの場合：
keras.optimizers.Adagrad(learning_rate=0.01)
・Adamの場合：
keras.optimizers.Adam(learning_rate=0.001, beta_1=0.9, beta_2=0.999, amsgrad=False)
####【実装演習の結果】
https://github.com/HienDT27/Rabbit-Challenge/blob/master/%E3%80%90%E6%B7%B1%E5%B1%A4%E5%AD%A6%E7%BF%92_Day_04%E3%80%914_3_keras_codes.ipynb
####【実装演習の考察】
#####① 線形回帰
$d = 0.5x + 2$の場合：
#####➁ 単純パーセプトロン
■ np.random.seed(0)をnp.random.seed(1)に変更すると、初期値の値が変わるので、学習の結果も変わっていく。今回では、np.random.seed(1)では、正解率が下がったことになる。
■ エポック数が大きいほど、正答率上がることが分かった。
■ XOR回路は線形分離可能ではないので、学習ができないことが確認できた。
■ OR回路では、バッチサイズを大きくする場合、エポック数が少ないと正答率が下がるが、エポック数が大きい場合は正答率が高くなっている。
#####③ 分類 (iris)
■ 中間層の活性関数をsigmoidに変更すると、学習後の精度が下がっている。
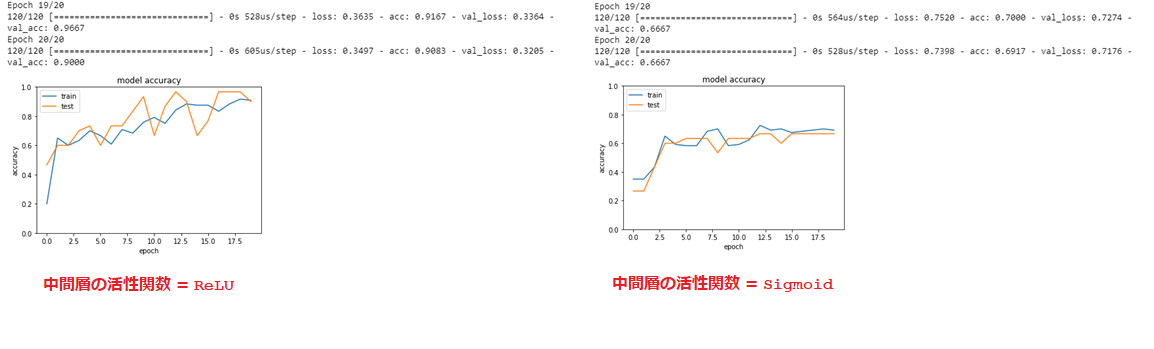
■ optimizerをSGD(lr=0.1)に変更すると、精度が良い時が得られるが、ばらつきが大きくなるとみられる。また、学習の速度を改善することが確認できた。
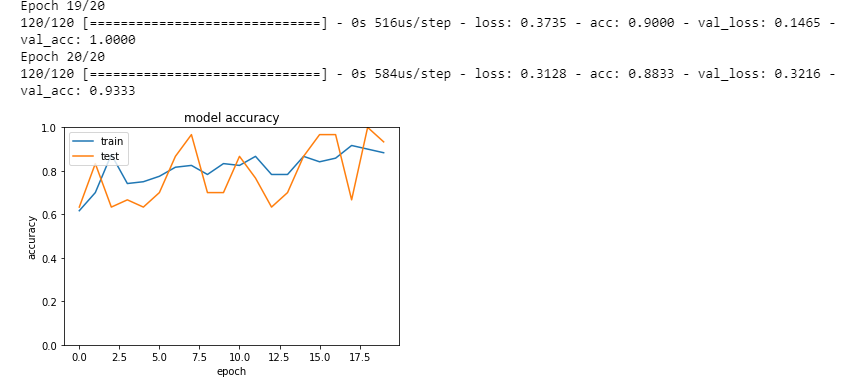
#####④ 分類 (mnist)
■ 誤差関数として categorical_crossentropy を使う場合はデータの形式を one_hot_label 形式に、sparse_categorical_crossentropy を使う場合はone_hot_labelではない 形式にしなければなりません。
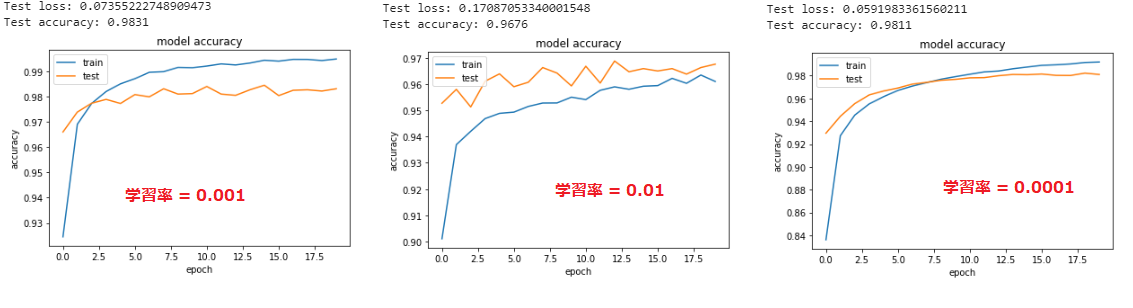
■ 誤差関数をsparse_categorical_crossentropyとして、学習率を$0.001 ➡ 0.01$ に変更する場合、正答率が下がっているし、トレニンーグデータに対してテストデータの方が正答率が高くなる。逆に、学習率を$0.001 ➡ 0.0001$ に変更すると、学習が遅くなっているが、最終的に精度が変わらなかった。
#####⑤ CNN分類 (mnist)
■ CNNのネットワークを使用すると、正答率が高くなｒ、99%以上も得られることが確認できた。
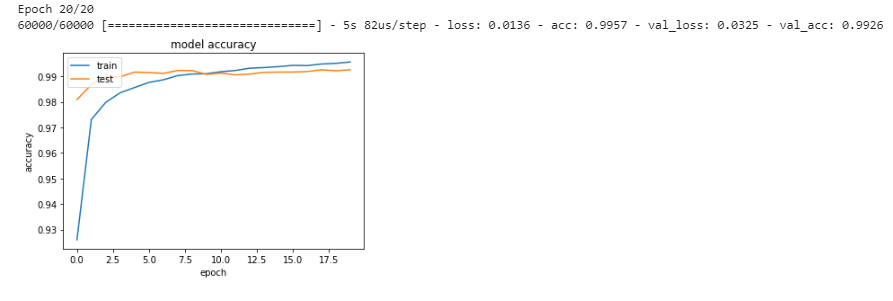
#####⑥ RNN（2進数足し算の予測）
■ 出力のノード数を増やすと、最初のepochでも精度が上がることが分かった。
■ RNNの出力活性化関数を sigmoid に変更場合、学習が進むが、精度がReLU関数より低かった。また、Tanh関数へ変更すると、精度の向上がReLU関数の場合とほぼ同じである（ただしepoch 1 は精度が低かった）
■ 最適化方法をadamに変更で、精度が良い結果である。
■ 入力ドロップアウトを0.5に設定した場合、学習が進まなくなった。
■ 再帰ドロップアウトを0.3に設定した場合、設定しない場合と比較で、学習は進むが正解率が落ちることが分かった。（Test accuracy: 0.9786853684951262）
■ RNNのunrollをTrueに設定しても、精度が下がらない結果が得た。
##Section 2：強化学習
###2-1) 強化学習とは
■ 長期的に報酬を最大化できるように環境のなかで行動を選択できるエージェントを作ることを目標とする機械学習の一分野
➡ 行動の結果として与えられる利益(報酬)をもとに、行動を決定する原理を改善していく仕組みです。
###2-2) 強化学習の応用例
マーケティングの場合
● 環境：会社の販売促進部
● エージェント：プロフィールと購入履歴に基づいて、キャンペーンメールを送る顧客を決めるソフトウェアである。
● 行動：顧客ごとに送信、非送信のふたつの行動を選ぶことになる。
● 報酬：キャンペーンのコストという負の報酬とキャンペーンで生み出されると推測される売上という正の報酬を受ける
###2-3) 探索と利用のトレードオフ
■ 環境について事前に完璧な知識があれば、最適な行動を予測し決定することは可能。
➡ どのような顧客にキャンペーンメールを送信すると、どのような行動を行うのかが既知である状況。
■ しかし、強化学習の場合、上記仮定は成り立たないとする。不完全な知識を元に行動しながら、データを収集。最適な行動を見つけていく。
■ トレードオフの関係性：
● 過去のデータで、ベストとされる行動のみを常に取り続ければ他にもっとベストな行動を見つけることはできない ➡ 探索が足りない状態
● 未知の行動のみを常に取り続ければ、過去の経験が活かせない ➡ 利用が足りない状態
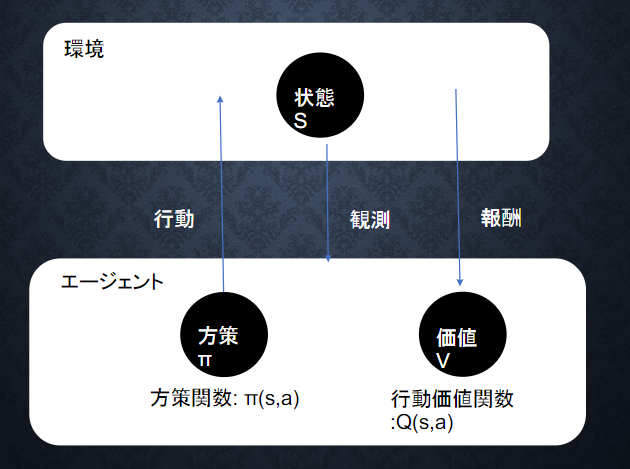
###2-4) 強化学習のイメージ
###2-5) 強化学習の差分
■ 強化学習と通常の教師あり、教師なし学習との違い ➡ 目標が違う
● 教師なし、あり学習では、データに含まれるパターンを見つけ出すおよびそのデータから予測することが目標
● 強化学習では、優れた方策を見つけることが目標
【強化学習の歴史】
■ 強化学習について
● 冬の時代があったが、計算速度の進展により大規模な状態をもつ場合の、強化学習を可能としつつある。
● 関数近似法と、Q学習を組み合わせる手法の登場
■ Q学習
● 行動価値関数を、行動する毎に更新することにより学習を進める方法
■ 関数近似法
● 価値関数や方策関数を関数近似する手法のこと
###2-6) 行動価値関数
■ 行動価値関数とは：価値を表す関数としては、状態価値関数と行動価値関数の2種類がある
● ある状態の価値に注目する場合は、状態価値関数である
● 状態と価値を組み合わせた価値に注目する場合は、行動価値関数である
###2-7) 方策関数
■ 方策関数とは
● 方策ベースの強化学習手法において、ある状態でどのような行動を採るのかの確率を与える関数のことです。
###2-8) 方策勾配法
■ 方策勾配法：
$${\theta^{(t+1)}=\theta^{(t)} + \epsilon\nabla J(\theta)
}$$
そこで、$J$ は方策の良さで、以下の方法で定義される。
● 平均報酬
● 割引報酬和
上記の定義に対応して、行動価値関数:$Q(s,a)$ の定義を行い。
方策勾配定理が成り立つ。
{\nabla _{\theta} J(\theta)=E_{\pi_{\theta}} [\nabla_{\theta} log\pi_\theta(a|s)Q^\pi(s,a))]
}
##Section 3：JDLA_Eシラバス_2020版より学習 (例題演習に関わる内容も含めた）
本章では、E資格の試験に向けて、JDLA_Eシラバス_2020版よりある項目が本講義では学習内容範囲外とするので、自分で調べて学習内容をまとめていきます。
JDLA_Eシラバス_2020版
###画像認識
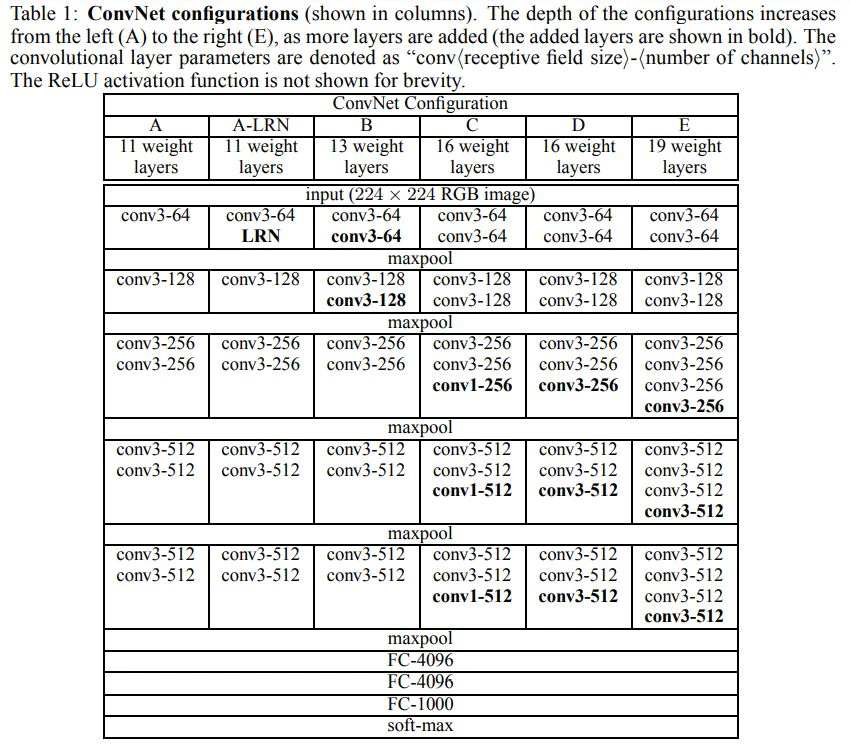
####【VGG】
■ VGG とは：2014年，画像認識のコンペティション(ILSVRC)のクラス分類の部門で特に高評価を得たネットワークです[1]．
[1]VGG : https://arxiv.org/pdf/1409.1556.pdf
■ 構成：
畳み込み層と全結合層を連結しシンプルに層を増やしたネットワーク構造である。層数については「16 weight layers」 等のいくつかのバリエーションがあります。
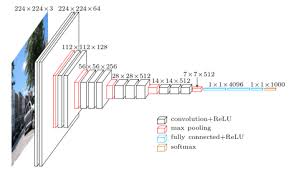
■ 構成のイメージ：
####【GoogLeNet】
GoogLeNet のアーキテクチャは、AlexNet、ZFnet などの既存のアーキテクチャとは大きく異なり、1×1 Convolution (Lin et al., 2014)、global average pooling (Lin et al., 2014)、および Inception モジュールなどの技術が新たに導入された。GoogLeNet は、この Inception モジュールを取り入れたことで、層を深くすることができるようになり、全体で 22 層で構成されている。
■ 1×1 Convolution：
1×1 Convolution は、入力画像のサイズを変えずに、チャンネルの数を変更する畳み込み操作である。チャンネル数を減らすことで、求めるべきパラメーター数が減り、次元削減の効果が現れる。
■ global average pooling：
最後の畳み込み層において、チャンネル数をクラス数と同じになるように畳み込み計算を行っている。その後、各チャンネルに対して、画素平均を計算し、最終的にはチャンネル数分の要素を持ったベクトルが得られる。このベクトルに対してソフトマックス関数を適用することで、クラスの分類結果が得られるようになる。
■ Inception モジュール：
Inceptionモジュールでは，ネットワークを分岐させ，サイズの異なる畳み込みを行った後，それらの出力をつなぎ合わせるという処理を行っている．この目的は，畳み込み層の重みをsparseにし，パラメータ数のトレードオフを改善することである．
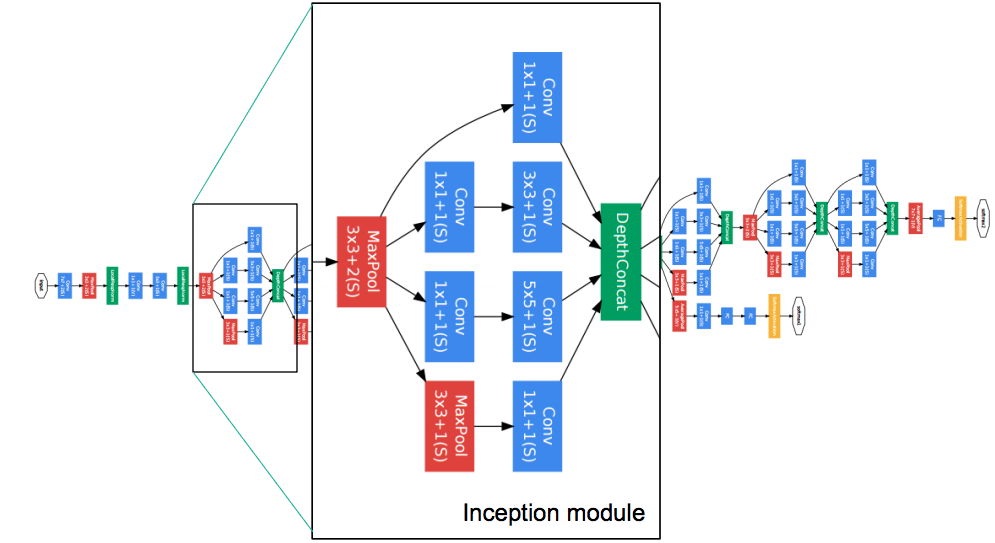
（参考）GoogLeNet / Inception
（参考）畳み込みニューラルネットワークの最新研究動向 (〜2017)
####【ResNet（Residual Network）】
■ 画像認識において一般にCNNの層数を増やすことでより高次元の特徴を獲得するが、単純に層を重ねるだけでは性能が悪化していくという問題がありました。（勾配消失問題）
➡ ResNetではshortcut connectionという機構を導入し、手前の層の入力を後ろの層に直接足し合わせることで、この勾配消失問題を解決できた。
■ shortcut connectionとは：
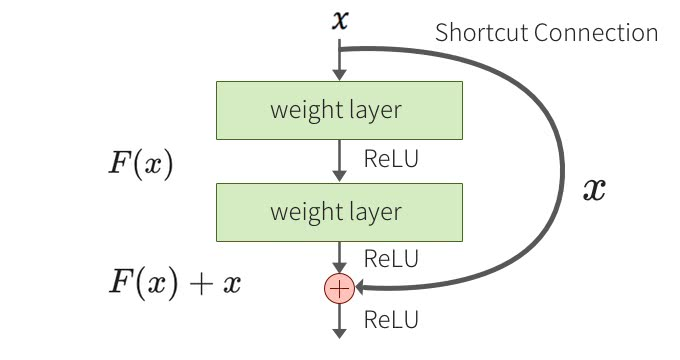
ショートカット接続はいくつかの層をスキップする単なる恒等写像です。パラメータの追加がなく、計算も複雑にならず、逆誤差伝播も可能なので実装も容易といったメリットがあります。
（参考）Residual Network(ResNet)の理解とチューニングのベストプラクティス
####【MobileNet】
【MobileNet-v1】
■ MobileNetはCNNの畳み込み演算を、Depthwise Separable Convolutionを利用することで、チャンネル方向が1（depthwise）の畳み込み演算と、空間方向が1（pointwise）の畳み込み演算に分解し、パラメータ数を削減できる。
■ Depthwise Convolution：
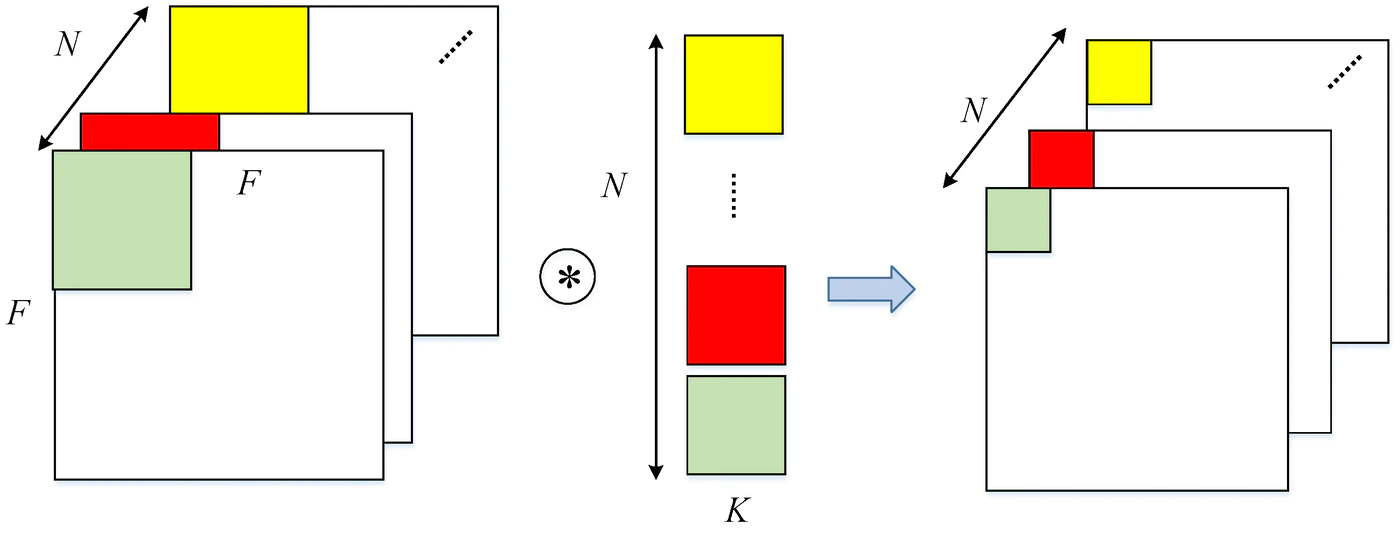
➡ 1チャネルに1つのフィルタが対応しており、各チャネルごとに対応したフィルタで畳み込みする。畳み込み処理はチャネルごとに独立しており、入力と出力のチャネル数は変わらない。
■ Pointwise Convolution (1x1 Convolution)：
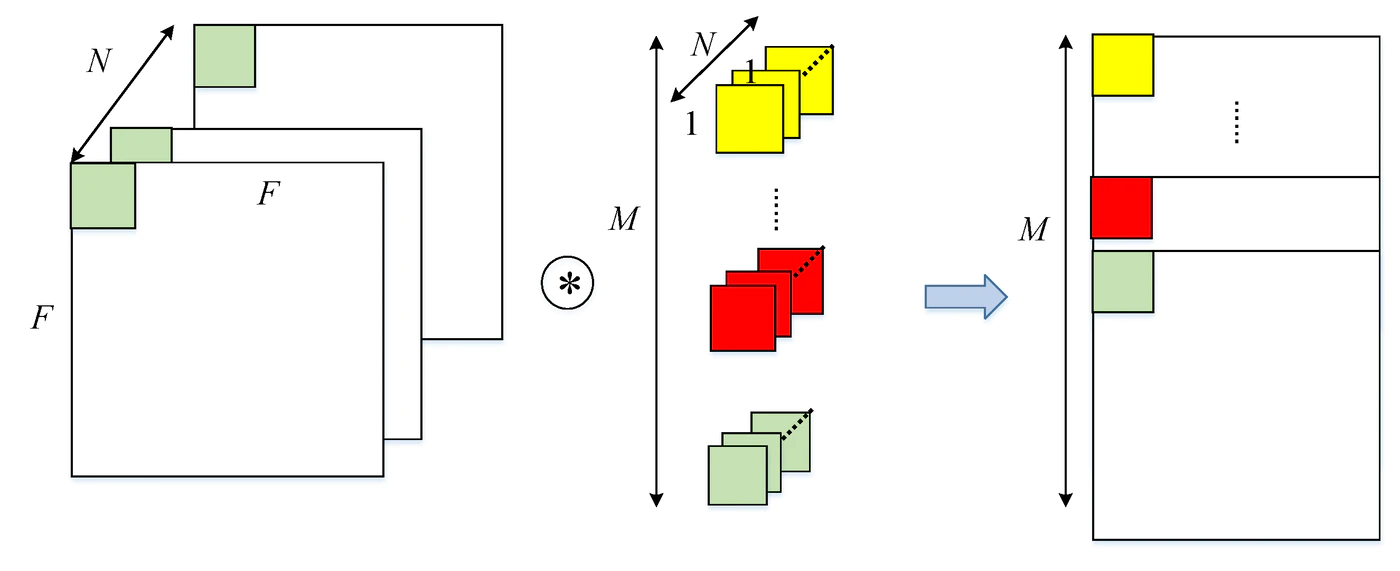
【MobileNet-v2】
■ Depthwise Separable Convolutionにおいて、Pointwise Convolutionの計算量(パラメータ数)が大きいため、これを減らす為に、Depthwise Separable Convolutionに代わってInverted Residualを導入した。
■ Inverted Residual Block：
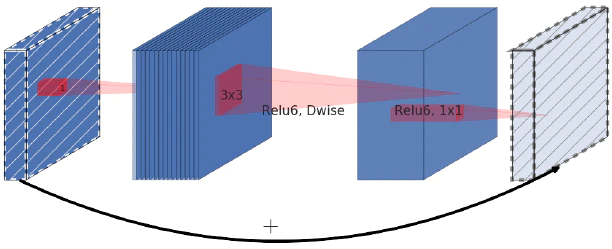
【MobileNet-v3】
● BottleneckへのSqueeze-and-Exciteモジュールの導入
● 活性化関数としてReLUの代わりに h-swishを使用
（参考）MobileNet(v1,v2,v3)を簡単に解説してみた
####【DenseNet】
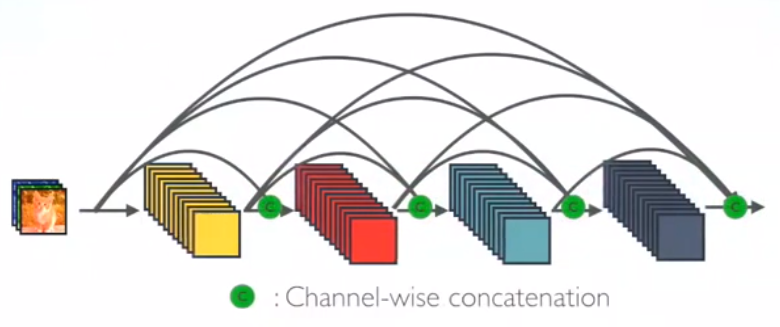
■ DenseNetはDense Block とTransition Layerの2つの部分で構成されています。
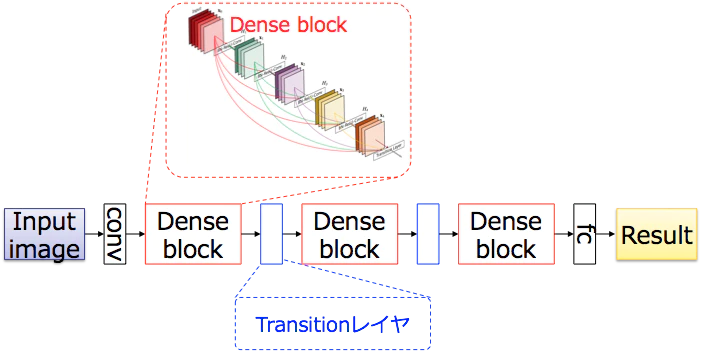
■ Dense Block ：
DenseNetにおいてはレイヤlの出力はレイヤ0、・・・l-2,l−1の出力をチャンネル方向に連結したものとなる。
■ Transition Layer：
DenseNetは，上記のDenseブロックを複数積み重ねることで構築され，各Denseブロックはtransitionレイヤにより接続される．
（参考）Review: DenseNet — Dense Convolutional Network (Image Classification)
（参考）畳み込みニューラルネットワークの最新研究動向 (〜2017)
###画像の局在化・検知・セグメンテーション
####【FasterR-CNN】
■ FasterR-CNNはCNN出力（特徴マップ）を元にregion proposal(物体があるっぽい領域を抽出）するモデルを構築している。実際のregion proposalは3~4層ほどのCNNで構成可能で小さい。
■ ネット構成：
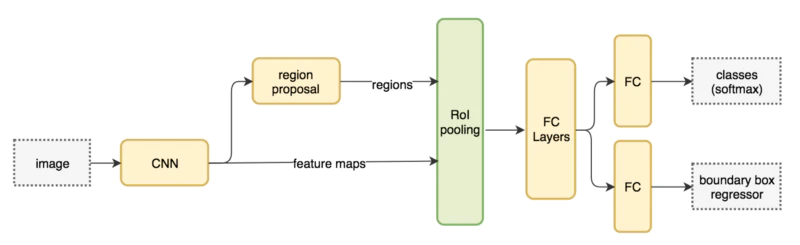
（参考)最新のRegion CNN(R-CNN)を用いた物体検出入門 ~物体検出とは? R-CNN, Fast R-CNN, Faster R-CNN, Mask R-CNN~
####【YOLO】
■ YOLOの特徴：
● 物体検出を分類問題ではなく回帰問題として初めてモデル化した
● 処理がひとつのネットワークのみで完結している
● リアルタイム処理が可能で精度も悪くない結果が出た
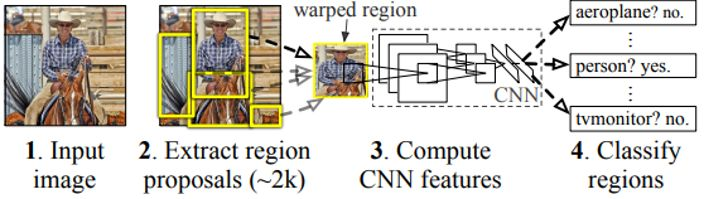
■ YOLO以前の物体検出手法は、物体検出を「分類問題」として扱うアプローチでした。
例）R-CNNの手法では、次のような手順で検出を行っているため、処理時間がかかってしまう問題点があります。
物体領域候補の提案 ⇒ CNNで特徴抽出 ⇒ 分類器で分類
一方、YOLOは次のような処理になっています。
画像をひとつのニューラルネットワークに入力するだけです。
■ ネットワーク構造：
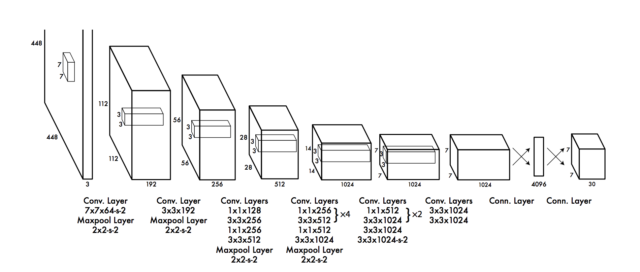
（参考)物体検出手法「YOLO」のアルゴリズムをざっくり解説する
（参考)【論文紹介】YOLOの論文を読んだので要点をまとめてみた