【ラビットチャレンジ】【深層学習】Day 02

ラビットチャレンジの提出レポートです。

<科目一覧>

深層学習：Day1 (NN)
深層学習：Day2 (CNN)
深層学習：Day3 (RNN)
深層学習：Day4 (Tensorflow & 強化学習)

１．要点まとめ

Section 1 : 勾配消失問題について

【活性化関数の選択】

■　シグモイド関数
　●　大きな値では出力の変化が微小なため、勾配消失問題を引き起こす事がある。
■　ReLU関数
　●　勾配消失問題の回避とスパース化に貢献することで良い成果をもたらしている。

【重みの初期値設定】

■　重みの初期値設定-Xavier
　●　Xavierの初期値を設定する際の活性化関数：
　　－　ReLU関数
　　－　シグモイド（ロジスティック）関数
　　－　双曲線正接関数

python

self.params['W1'] = np.random.randn(input_size, hidden_size) / nq.sqrt(input_layer_size)
self.params['W2'] = np.random.randn(hidden_size, output_size) / nq.sqrt(hidden_layer_size)

■　重みの初期値設定-He
　●　Heの初期値を設定する際の活性化関数：ReLU関数

python

self.params['W1'] = np.random.randn(input_size, hidden_size) / nq.sqrt(input_layer_size)*np.sqrt(2)
self.params['W2'] = np.random.randn(hidden_size, output_size) / nq.sqrt(hidden_layer_size)*np.sqrt(2)

【バッチ正規化】

■　バッチ正規化とは?
　●　ミニバッチ単位で、入力値のデータの偏りを抑制する手法
■　バッチ正規化の使い所とは?
　●　活性化関数に値を渡す前後に、バッチ正規化の処理を孕んだ層を加える

Section 2 : 学習率最適化手法について

【復習】
■　学習率の値が大きい場合：最適値にいつまでもたどり着かず発散してしまう。
■　学習率の値が小さい場合
　●　発散することはないが、小さすぎると収束するまでに時間がかかっ てしまう。
　●　大域局所最適値に収束しづらくなる

【モメンタム】

■　誤差をパラメータで微分したもの と学習率の積を減算した後、現在 の重みに前回の重みを減算した値 と慣性の積を加算する
$$w^{(t + 1)} = w^{(t)} + V_t$$
そこで、$V_t = \mu V_{t-1} - \epsilon \nabla E$ .
$\mu$は慣性
■　モメンタムのメリット
　●　局所的最適解にはならず、大域的最適解となる
　●　谷間についてから最も低い位置(最適値)にいくまでの時間が早い

【AdaGrad】

■　誤差をパラメータで微分したものと再定義した学習率の積を減算する

■　AdaGradのメリット：
勾配の緩やかな斜面に対して、最適値に近づける
■　AdaGradの問題点：
学習率が徐々に小さくなるので、鞍点問題を引き起こす事がある

【RMSProp】

■　誤差をパラメータで微分したものと再定義した学習率の積を減算する

■　RMSPropのメリット
　●　局所的最適解にはならず、大域的最適解となる。
　●　ハイパーパラメータの調整が必要な場合が少ない。

【Adam】

■　Adamとは？
　●　モメンタムの、過去の勾配の指数関数的減衰平均
　●　RMSPropの、過去の勾配の2乗の指数関数的減衰平均
上記をそれぞれ孕んだ最適化アルゴリズムである。
■　Adamのメリットとは？
　●　モメンタムおよびRMSPropのメリットを孕んだアルゴリズムである

Section 3 : 過学習について

【復習】
過学習とはテスト誤差と訓練誤差とで学習曲線が乖離すること。原因は以下のように挙げられる。
　●　パラメータの数が多い
　●　パラメータの値が適切でない
　●　ノードが多い

【L1正則化、L2正則化】

■　Weight decay(荷重減衰)：
　●　過学習の原因：重みが大きい値をとることで、過学習が発生することがある
　●　過学習の解決策：誤差に対して、正則化項を加算することで、重みを抑制する
■　L1 / L2 正則化：

E_{n}(w) + \frac{1}{p}\lambda || x || _p \\
||x||_p = (|x_1|^p + |x_2|^p + ・・・+|x_n|^p)^{\frac{1}{p}} = ( \sum_{i=1}^{n} |x_i|^p ) ^ {\frac{1}{p}}

　●　$p=1$ の場合、L1正規化と呼ぶ。
　●　$p=2$ の場合、L2正規化と呼ぶ。

【ドロップアウト】

■　ドロップアウトとは?
　●　ランダムにノードを削除して学習させること
■　ドロップアウトのメリット
　●　リットとしてデータ量を変化させずに、異なるモデルを学習させていると解釈できる

Section 4 : 畳み込みニューラルネットワークの概念

【畳み込み層の全体像】

畳み込み層

　●　畳み込み層では、画像の場合、縦、横、チャンネルの3次元 のデータをそのまま学習し、次に伝えることができる。
　●　結論:3次元の空間情報も学習できるような層が畳み込み層である。
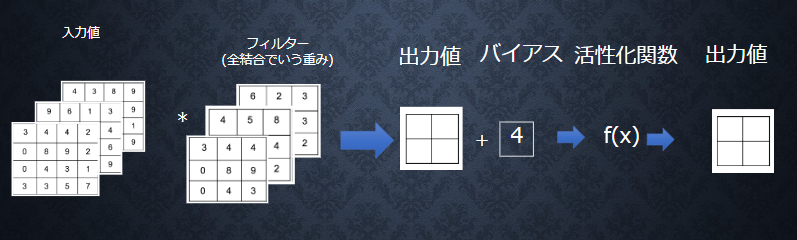
■【畳み込み層演算概念(バイアス)】

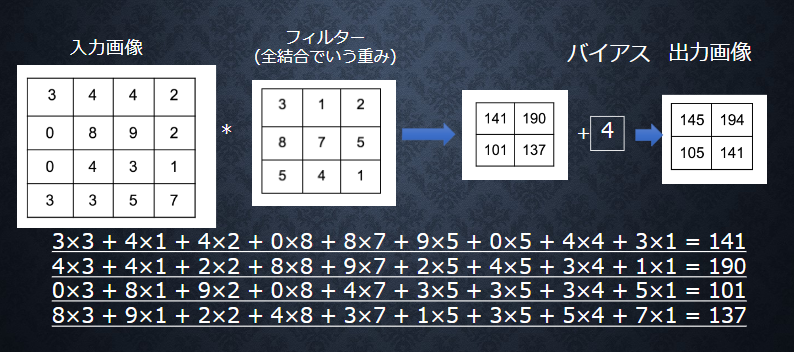
■【畳み込み層演算概念(パディング)】

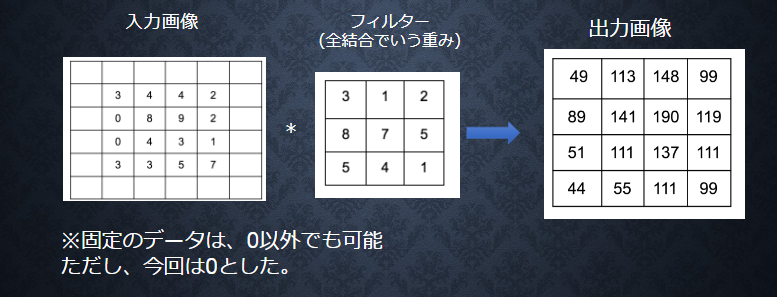
■【畳み込み層演算概念(パディング)】

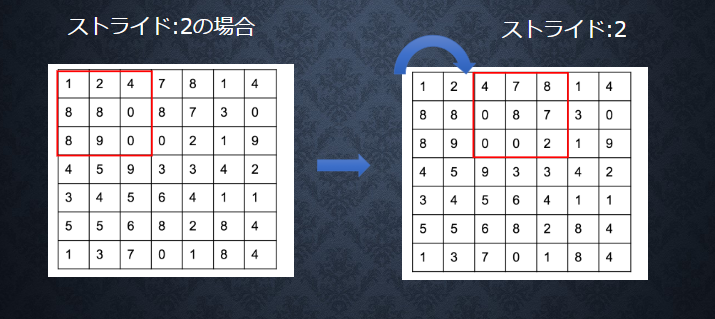
■【畳み込み層演算概念(チャンネル)】

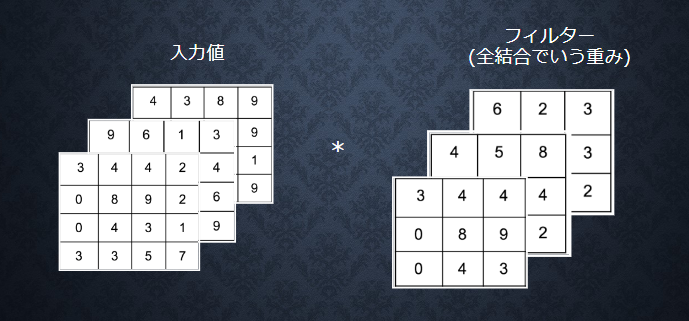
■　全結合層のデメリットについて、画像の場合、縦、横、チャンネルの3次元データだが、1次元のデータとして処理されるため、RGBの各チャンネル間の関連性が、学習に反映されないということ。

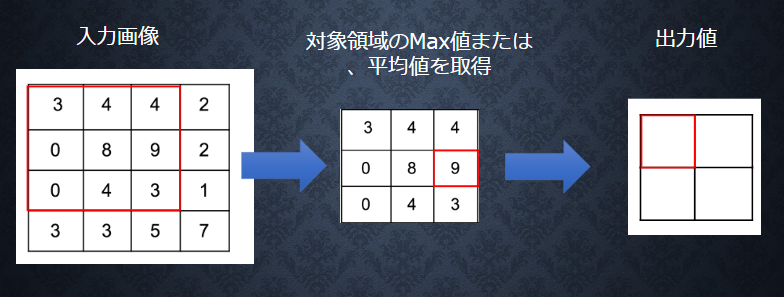
プーリング層

Section 5 : 最新のCNN

【AlexNet】
■　モデルの構造：
　●　5層の畳み込み層およびプーリング層な ど、それに続く3層の全結合層から構成 される。
■　過学習を防ぐ施策：
　●　サイズ4096の全結合層の出力にドロップアウトを使用している。

2．確認テスト

Section 1 : 勾配消失問題について

【P12】
Q：連鎖律の原理を使い、dz/dxを求めよ。

 z = t^2 \\ 
t = x + y

A：
$$\dfrac{\partial z}{\partial x}=\dfrac{\partial z}{\partial t}\dfrac{\partial t}{\partial x} =2t = 2(x +y)$$
【P20】
Q：シグモイド関数を微分した時、入力値が0の時に最大値をとる。その値 として正しいものを選択肢から選べ。
（1）0.15 （2）0.25 （3）0.35 （4）0.45
A：

 f(z) = Sigmoid(z)　➡ f(0) = 1/2 \\ 
{f(z)' = (1 - f(z)) \cdot f(z) =1/4
}

【P28】
Q：重みの初期値に0を設定すると、どのような問題が発生するか。簡潔に説明せよ。
A：すべての値が同じ値で伝わるため、パラメータのチューニングが行われなくなる。
【P31】
Q：一般的に考えられるバッチ正規化の効果を2点挙げよ。
A：
　●　計算の高速化
　●　勾配消失が起きづらくなる

Section 2 : 学習率最適化手法について

【P47】
Q：モメンタム・AdaGrad・RMSPropの特徴をそれぞれ簡潔に説明せよ。
A：
■　【モメンタム】：谷間についてから最も低い位置(最適値)にいくまでの時間が早い
■　【AdaGrad」：勾配の緩やかな斜面に対して、最適値に近づける
■　【RMSProp】：ハイパーパラメータの調整が必要な場合が少ない。

Section 3 : 過学習について

【P63】
Q：リッジ回帰の特徴として正しいものを選択しなさい？
A：(a) ハイパーパラメータを大きな値に設定すると、すべての重みが限りなく0に近づく
【P68】
Q：下図について、L1正則化を表しているグラフはどちらか答えよ。

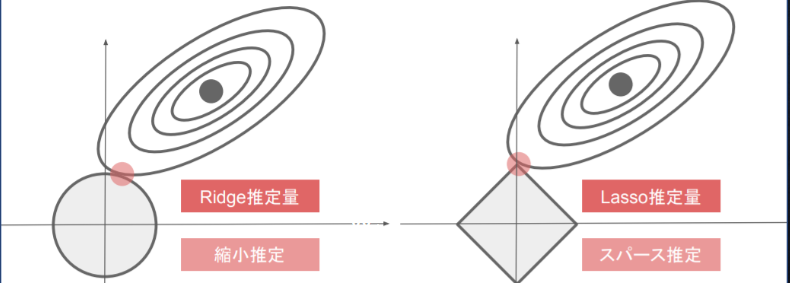
A：
　●　左図はRidge推定量のグラフ（縮小推定）　➡　L2 正則化
　●　右図はLasso推定量のグラフ（スパース推定）➡　L1 正則化

Section 4 : 畳み込みニューラルネットワークの概念

【P100】
Q：サイズ6×6の入力画像を、サイズ2×2のフィルタで畳み込んだ時の出力画像のサイズを答えよ。なおストライドとパディングは1とする。
A：入力サイズ=(H, W), フィルターサイズ＝(FH, FW), 出力サイズ=(OH, OW)、パディングをP, ストライドをSとすると、以下の式に書ける。

{ OH =\frac{H+2P-FH}{S}+1} \\
{ OW =\frac{W+2P-FW}{S}+1}

上式によると、出力画像のサイズ 7x7となる。

３．実装演習

DN23_Jupyter演習

【実装結果】

【考察】

■　初期化をGaussで、活性化関数をSigmoid をすると、勾配消失問題が出ているため、学習が進まななかった。
➡　初期化をXavierを変更すると（活性化関数はSigmoid）、勾配消失問題が行わなく、学習が進んでいるが、学習（またはテスト）での正答率が高くない（正答率が0.8ぐらいでした）
■　活性化関数をReLUで、初期化方法をGaussでもHeでも、学習がうまく進んで行くし、良い正答率が得られた（90％以上）。ただし、ReLU-He では、ReLU-Gaussより学習が早くて、正答率が高いとみられる。

DN26_Jupyter演習(2)

【実装結果】

【考察】

■　勾配消失問題より学習が進まないモデルに対して、学習率最適化手法（モメンタム、AdaGrad、RMSProp、Adam）を適用すると、勾配消失問題を回避することができる。
■　上記の4つの学習率最適化手法の中には、モメンタム、AdaGrad手法よりもRMSProp、Adam手法の方が学習が早いし、正答率（モデルの評価）も高くなると見られる。
■　さらに、Adam手法に対して、活性化関数をSigmoid　⇒　ReLU、初期化方法をGauss　⇒He に変更してみると、モデルの正答率が少し上がった（94％　⇒　96％）し、最初のepochでも正答率が高い（学習が早い）と分かった。

DN32_Jupyter演習(Dropout)

【実装結果】

【考察】

■　過学習に対しては、正則化手法（L1・L2正則化、ドロップアウト）を適用すれば、抑制することができる。
■　正則化 (L1・L2) に関してのweight_decay_lambdaバラメータ、ドロップアウト手法に関してのdropout_ratioパラメータの値を調整すると、過学習を抑制できる。ただし、それらのパラメータの値が大きいほど、モデルの精度が下がる。
パラメータの値がそのまま大きい値にすると、モデルの精度を上げるためには、学習率最適化手法（今回実装にはAdamを使った）を適用として工夫する必要がある。
■　L1・L2正則化、ドロップアウトを組み合わせて使うことができる。

DN35_Jupyter演習(im2col)～DN37_Jupyter演習(3)

【実装結果】

【考察】

■　im2col：多次元データを２次元化する。
　●　メリット：行列計算に落とし込むことで多くのライブラリを活用できる。
　●　デメリット：通常よりも多くのメモリを消費する
■　col2im：２次元データを多次元化する
■　MNISTデータセットに対して、Simple convolution networkを利用すると、正答率は96.5％という結果になる。

(Sample) Deep Convolution Net

【実装結果】

【考察】

■　Deep convolution networkを利用することで、認識率98％の精度が得られた。
（学習時間がかかる）

４．例題チャレンジ・参考文献（図書）など

【例題チャレンジ】

【例題 01】

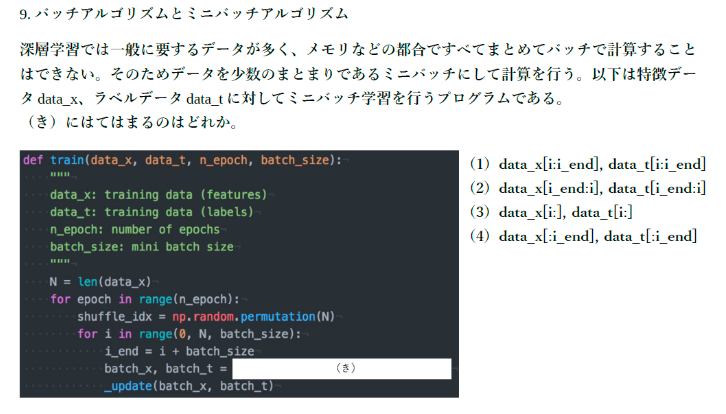
⇒　回答：バッチサイズだけデータを取り出す処理であるので、
答えは　data_x[i:i_end], data_t[i:i_end]となる。
【例題 02】

4L2$ノルムは、$||param||^2$ であり、その勾配(微分値)が誤差の勾配に加えられるので、答えは（４）となる。
【例題 03】

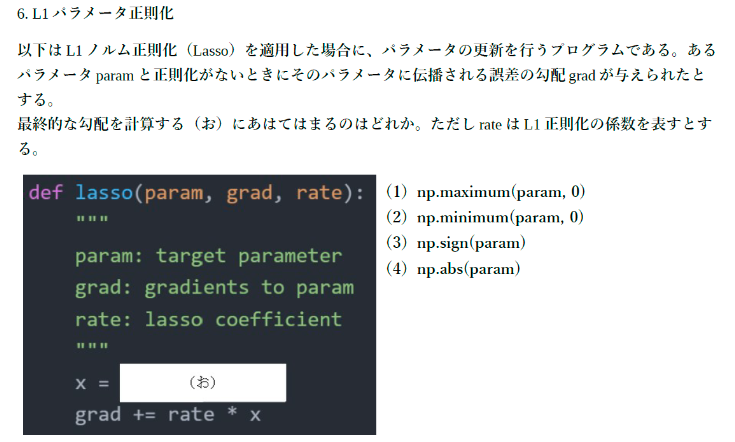
$L1$ノルムは、|param|なのでその勾配が誤差の勾配に加えられるので、答えは（３）np.sign(param)となる。
【例題 04】

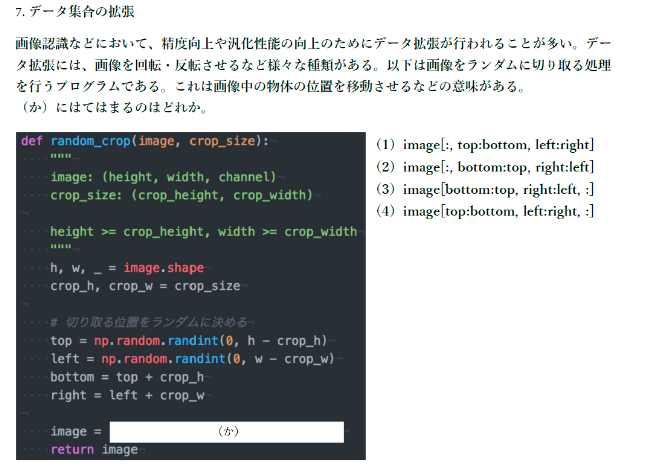
imageの形式が(縦幅, 横幅, チャンネル)であるのも考慮すると、答えは（４）
image[top:bottom, left:right, :]

【参考文献（図書）】

●　Convolutional Neural Networksコース（Coursera)
https://www.coursera.org/learn/convolutional-neural-networks
●　（本）ゼロから作るDeep Learning
――Pythonで学ぶディープラーニングの理論と実装

５．JDLA_Eシラバス_2020版より学習

本章では、E資格の試験に向けて、JDLA_Eシラバス_2020版よりある項目が本講義では学習内容範囲外とするので、自分で調べて学習内容をまとめていきます。
JDLA_Eシラバス_2020版

【ネステロフのモメンタム】

■　モメンタムSGDの修正版であり，さらに収束への加速を増したものである。
■　数式で表すと、以下のように書ける
　●　モメンタム法での更新：

{\begin{align}
\boldsymbol{x}_{k+1} &= \boldsymbol{x}_k - \eta \bigtriangledown f(\boldsymbol{x}_k) + \alpha \Delta \boldsymbol{x}_k
\end{align}
}

　●　ネステロフのモメンタム法での更新：

{\begin{align}
\boldsymbol{x}_{k+1}
 &= \boldsymbol{x}_k - \eta \bigtriangledown f(\bar{\boldsymbol{x}}_k) + \gamma_k \Delta \boldsymbol{x}_k\\
\bar{\boldsymbol{x}}_k &= \boldsymbol{x}_k + \gamma_k \Delta \boldsymbol{x}_k
\end{align}\\
}

モメンタム法と違うのは、勾配を計算する位置にある。

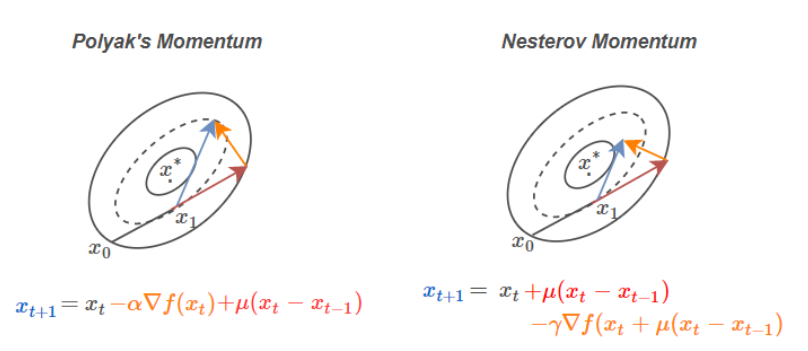
（参考）Nesterov’s Accelerated Gradient, Stochastic Gradient Descent

【半教師あり学習】

■　半教師あり学習とは
少量のラベルありデータを用いることで大量のラベルなしデータをより学習に活かせることができる学習方法です。
■　メリット：
　●　ラベルありデータとラベルなしデータの両方を使って学習ができるため、学習データが不足しているときに有効活用できる可能性がある
　●　大量のデータにラベルを付与してラベルありデータを作るという作業を軽減できる
■　半教師あり学習の手法は大きく次の二つに分かれます。：
　●　ブートストラップ法（分類器に基づく手法）
　●　データに基づく手法
①　ブートストラップ法（分類器に基づく手法）
　●　ラベルなしデータに対してラベルを付与して、どんどん訓練データを増やしながら自ら学習していく
　●　処理の流れ：

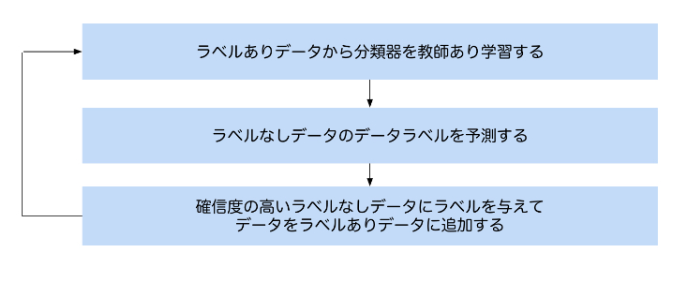
② データに基づく手法
　●　ラベルなしデータからデータの表現方法、分布を獲得してそれを用いて教師あり学習を行う方法です

【早期終了】

エポック数を回し切った最後のパラメタではなく， 検証誤差が最少となったエポックでのパラメタを返す手法を早期終了という． 早期終了はその単純さと有効性から，深層学習において一般的に最も使われている正則化である
（参考）機械学習，正則化についてまとめ

【バギングやその他のアンサンブル手法】

■　アンサンブル学習とは？
　●　複数のモデル（学習器）を融合させて1つの学習モデルを生成する手法です。
　●　アンサンブル学習を行うことで精度の低いモデル（弱学習器）でも高精度を実現することができます。
　●　アンサンブル学習の種類：バギング、ブースティング、スタッキング
■　バイアス（Bias）」と「バリアンス（Variance）」
　●　バイアスは、予測値と実測値の差を表す。バイアスが低ければ低いほど上手く予測出来ているということになります。
　●　バリアンスは、予測値のばらつきを表します。複雑なモデルを組んで様々なデータへフィッティングさせようとすると予測値がばらつきバリアンスは高くなります。
■　バギング：
　●　一般的にモデルの予測結果のバリアンスを低くする特徴があります。
　●　バギングではブートストラップ手法を用いて学習データを復元抽出することによってデータセットに多様性を持たせています。復元抽出とは、一度抽出したサンプルが再び抽出の対象になるような抽出方法です。
■　ブースティング：
　●　一般的にモデルの予測精度に対してバイアスを下げる特徴があります。
　●　ブースティングは基本となるモデルを最初に訓練してベースラインを設けます。このベースラインとした基本モデルに対して何度も反復処理を行い改善を行なっていきます。
■　スタッキング：
　●　スタッキングとは言葉の通りモデルを積み上げていく方法です。上手く利用することによりバイアスとバリアンスをバランスよく調整する事が可能です。
（参考）機械学習上級者は皆使ってる？！アンサンブル学習の仕組みと3つの種類について解説します