【ラビットチャレンジ】【深層学習】Day 01

ラビットチャレンジの提出レポートです。

##<科目一覧>
深層学習：Day1 (NN)
深層学習：Day2 (CNN)
深層学習：Day3 (RNN)
深層学習：Day4 (Tensorflow & 強化学習)
##１．要点まとめ

Section 1 : 入力層 ～ 中間層

■　入力層は外部からの情報（説明変数）を示す。
例）動物種類分類問題では、体長、体重、ひげの本数、耳の大きさなどの情報
■　中間層は入力層からの情報（説明関数）に重みを掛け合わせ、バイアスを足して活性化関数により変換され、次の層へ情報を送信する。
■　中間層は人の目には見えなく、隠れ層と呼ぶこともある。
■　入力 $x_1 ,x_2 ,x_3 ,・・・$ 、重み　$w_1 ,w_2 ,w_3 ,・・・$、バイアス　$b$　とすると、総入力　$u$ は以下の通りになる
$$u = w_1x_1 + w_2x_2 + w_3x_3 + ・・・ +b = Wx + b$$

Section 2 : 活性化関数

■　活性化関数は入力信号の総和を出力信号に変換する関数
■　ニューラルネットワークでは、活性化関数に非線形関数を用いる必要がある
　●　理由：線形関数を用いると、ニューラルネットワークで層を深くすることの意味がなくなってしまう。（どんなに層を深くしても、それと同じことを行う）
■　中間層用の活性化関数
　●　ReLU関数
　●　シグモイド(ロジスティック)関数
　●　ステップ関数
■　ステップ関数
　●　数式：

f(x) = \left\{
\begin{array}{ll}
1 & (x \geq 0) \\
0 & (x \lt 0)
\end{array}
\right.

　●　0－1間の間を表現できず、線形分離可能なものしか学習できなかった。
■　シグモイド関数
　●　数式
$$f(x)=\dfrac{1}{1+e^{-x}}$$
　●　0 ~ 1の間を緩やかに変化する関数で、ステップ関数ではON/OFFしかない状態に対し、信号の強弱を伝えられるようになる。
　●　大きな値では出力の変化が微小なため、勾配消失問題を引き起こす事があった。
■　ReLU関数
　●　数式

{f(x) = \left\{\begin{array}{ll}x & (x \gt 0) \\0 & (x \leq 0)\end{array}\right.}

　●　今最も使われている活性化関数
　●　勾配消失問題の回避とスパース化に貢献することで良い成果をもたらしている。

Section 3 : 出力層

####誤差関数
■　誤差関数= 二乗誤差の場合、以下の数式とコードで表す
$${E_n(w)=\frac{1}{2}\sum_{j=1}^{J} (y_j-d_j)^2 = \frac{1}{2}||(y-d)||^2
}$$

python

loss = functions.mean_squared_error(d, y)

■　誤差関数= クロスエントロピー誤差の場合、以下の数式とコードで表す
$${E_n(w)=-\sum_{i=1}^Id_ilog y_i
}$$

python

loss =cross_entropy_error(d,y)

####出力層の活性化関数
■　出力層と中間層との違い
　●【値の強弱】
　ー　中間層︓しきい値の前後で信号の強弱を調整
　ー　出力層︓信号の大きさ（比率）はそのままに変換
　●【確率出力】
　－　分類問題の場合、出力層の出力は0 ~ 1 の範囲に限定し、総和を１とする必要がある
　－　出力層と中間層で利用される活性化関数が異なる
■　出力層用の活性化関数
　●　ソフトマックス関数（多クラス分類）
　●　恒等写像（回帰）
　●　シグモイド(ロジスティック)関数（二値分類）
■　ソフトマックス関数
　●　数式：

f(i,u)=\frac{\exp(u_i)}{\sum_{k=1}^{K}\exp(u_k)}

　●　ソフトマックス関数の出力は０～１の間の実数になり、総和が１となる。

Section 4 : 勾配降下法

####勾配下降法
■　深層学習の目的は学習を通じて、誤差を最小にするネットワークを作成すること。
勾配降下法を使って最適なパラメータを求めることができる。
■　勾配下降法：$$W^{(t+1)} =W^{(t)}-\varepsilon\nabla E$$
　●　$\varepsilon$　は学習率。
学習率の値によって学習の効果が大きく変わる。学習率が大きすぎた場合、勾配の移動は大きくなり、発散する可能性が高い。逆に、学習率が小さい場合は、発散することが起きないが、収束するまでにじかんがかかる。
　●　勾配　$\nabla E=\frac{\partial E}{\partial W}=[\frac{\partial E}{\partial w_1}･･･\frac{\partial E}{\partial w_M}]$
####確率的勾配降下法
$$W^{(t+1)} =W^{(t)}-\varepsilon\nabla E_n$$
■　確率的勾配降下法のメリット
　●　データが多い場合、計算コストが減らせる（全データの利用ではないから）
　●　望まない局所極小解に収束するリスクの軽減
　●　オンライン学習ができる
####ミニバッチ勾配降下法
$$W^{(t+1)} =W^{(t)}-\varepsilon\nabla E_t$$
そこで、$E_t=\frac{1}{N_t}\sum_{n\in D_t}E_n$ , $ N_t=|D_t|$
■　学習データをランダムに分割したデータの集合(ミニバッチ)$D_t$を利用して、勾配降下法を行う。
■　ミニバッチ勾配降下法では、確率的勾配降下法のメリットを損なわず、計算機の計算資源を有効利用できる

Section 5 : 誤差逆伝番法

■　【誤差逆伝播法】
算出された誤差を、出力層側から順に微分し、前の層前の層へと伝播。最小限の計算で各パラメータでの微分値を解析的に計算する手法

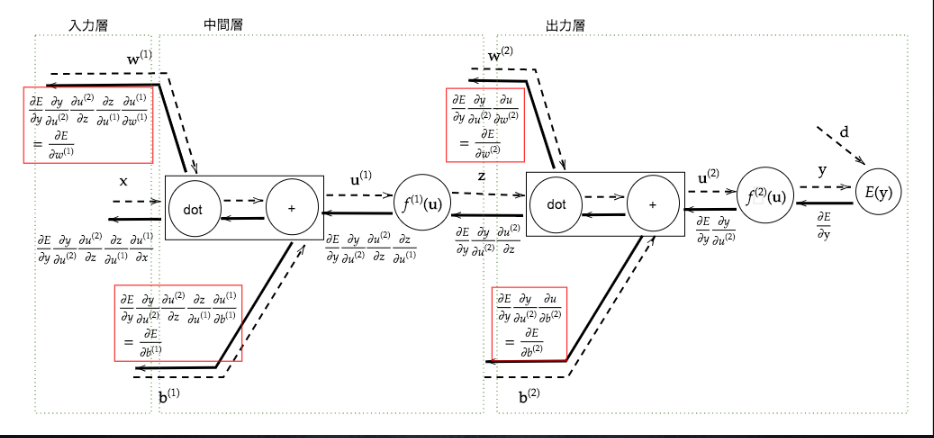
計算結果（=誤差）から微分を逆算することで、不要な再帰的計算を避けて微分を算出できる

２．確認テスト

Section 1 : 入力層 ～ 中間層

【P10】
**Q：**ディープラーニングは、結局何をやろうとしているか2行以内で述べよ。
また、次の中のどの値の最適化が最終目的か。 全て選べ。
①入力値[ X] 、②出力値[ Y] 、③重み[W]、④バイアス[b]、 ⑤総入力[u]、 ⑥中間層入力[ z] ⑦学習率[ρ]
**A：**ディープラーニングは誤差を最小化するパラメータを見つけること。
また、値の最適化の最終目的：③重み[W]、④バイアス[b]
【P12】
**Q：**次のネットワークを紙にかけ。
　●　入力層：2ノード1層
　●　中間層：３ノード2層
　●　出力層：1ノード1層
A：

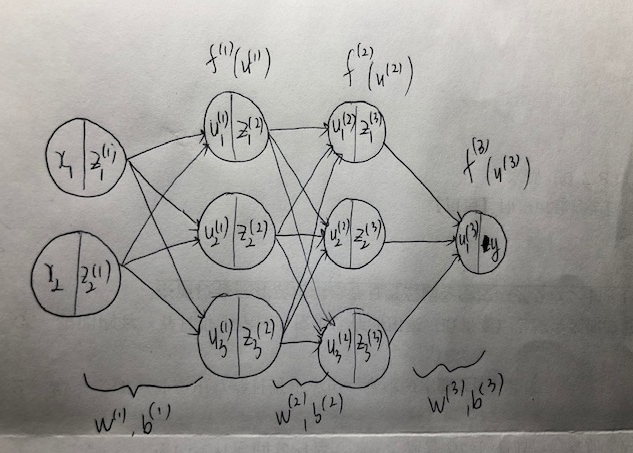
【P19】
**Q：**この図式に動物分類の実例を入れてみよう。
**A：**以下の図にかける

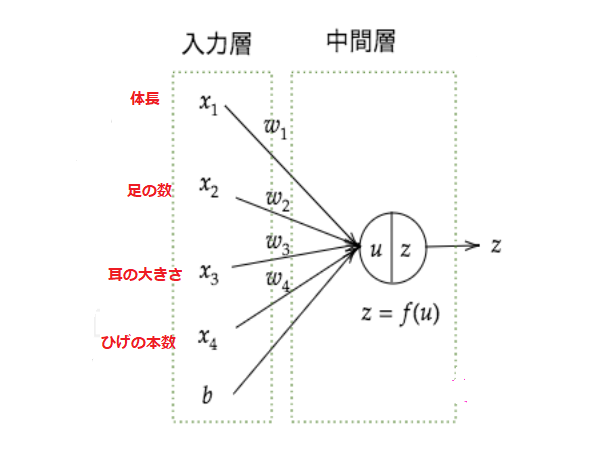
【P21】
**Q：**この数式をPythonで書け。
$${u=w_1x_1+w_2x_2+w_3x_3+w_4x_4+b=Wx+b..(1.2)
}$$
A：$$u = np.dot(x, W) + b$$
【P23】
**Q：**1-1のファイルから 中間層の出力を定義しているソースを抜き出せ。
**A：**以下の通りです。

#中間層出力
z = functions.relu(u)
print_vec("中間層出力", z)

Section 2 : 活性化関数

【P26】
**Q：**線形と非線形の違いを図にかいて簡易に説明せよ。
**A：**線形関数は以下の2つの式が成り立つ
　●　任意の $x , y$ に対して $f(x + y) = f(x) + f(y)$
　●　任意の $x$ 、任意のスカラー $k$ に対して $ f(kx) = kf(x)$
上記の式に成り立たないと、非線形関数となる。

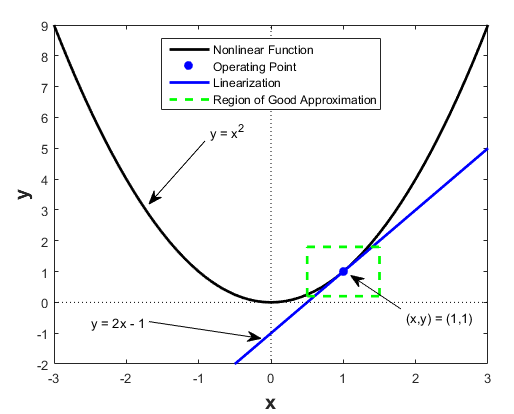
【P33】
**Q：**配布されたソースコードより該当する箇所を抜き出せ。
**A：**以下の通りです。

z1 = functions.sigmoid(u)

Section 3 : 出力層

【P44】
Q：
　●　なぜ、引き算でなく二乗するか述べよ
　●　下式の1/2はどういう意味を持つか述べよ
$${E_n(w)=\frac{1}{2}\sum_{j=1}^{J} (y_j-d_j)^2 = \frac{1}{2}||(y-d)||^2
}$$
A：
　●　損失関数はマイナスの値にならないので、引き算で表すことができない。
また、損失関数は絶対値（abs関数）を取ると、微分不可能な点がある（関数 $f(x) = |x|はx = 0で微分可能でない$)ので、二乗にした方が良い。
　●　二乗の関数に1/2をかけると、微分したときに、計算しやすくなる。
【P51】
**Q：**①～③の数式に該当するソースコードを示し、一行ずつ説明せよ

python

def softmax(x):
   if x.ndim == 2:#2次元だった場合
     x = x.Tx
     x = x-np.max(x, axis=0)
     y = np.exp(x) /np.sum(np.exp(x), axis=0) #①～③の数式に該当するソースコード
      return y.T　#①～③の数式に該当するソースコード
 x = x -np.max(x) # オーバーフロー対策
      return np.exp(x) / np.sum(np.exp(x)) 

A：
①　 return y.T：softmax関数の結果を返す
➁　np.exp(x)：NumPy の exp 関数を利用している
③　np.sum(np.exp(x), axis=0)：全ての$u$をNumPy の exp 関数で計算し、総和をとる。
【P53】
**Q：**①~②の数式に該当するソースコードを示し、一行づつ処理の説明をせよ。

python

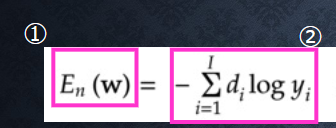
# クロスエントロピー
def cross_entropy_error(d, y):
    if y.ndim == 1:
        d = d.reshape(1, d.size)
        y = y.reshape(1, y.size)
    # 教師データがone-hot-vectorの場合、正解ラベルのインデックスに変換
    if d.size == y.size:
        d = d.argmax(axis=1)
    batch_size = y.shape[0]
    return -np.sum(np.log(y[np.arange(batch_size), d] + 1e-7)) / batch_size

**A：**①~②の数式に該当するソースコード
return -np.sum(np.log(y[np.arange(batch_size), d] + 1e-7)) / batch_size
　●　Log部分がゼロにならないように、$(1e-7)$という数字を追加する。

Section 4 : 勾配降下法

【P56】
**Q：**以下の式に該当するソースコードを探してみよう。
$$ W^{(t+1)} =W^{(t)}-\varepsilon\nabla E$$
**A：**network[key] -= learning_rate * grad[key]
【P65】
**Q：**オンライン学習とは何か2行でまとめよ
A：
　●　オンライン学習とは学習データが入ってくるたびにその都度、新たに入ってきたデータのみを使って学習を行うものになります。
　●　オンライン学習はバッチ学習と違いのは、学習を行う際に1からモデルを作り直すのではなく、そのデータによる学習で今あるモデルのパラメータを随時更新していくと流れになります。
（参考）オンライン学習とバッチ学習
【P68】
**Q：**この数式の意味を図に書いて説明せよ。
$$W^{(t+1)} =W^{(t)}-\varepsilon\nabla E_t$$
A：
　(〇〇〇)　　　　　　(〇〇〇)　　　　　　　(〇〇〇)
サンプリング１　　　サンプリング２　　　　サンプリング３
上記の任意のサンプリングの一つをミニバッチとして勾配降下法の平均誤差を計算する。

Section 5 : 誤差逆伝番法

【P78】
**Q：**誤差逆伝播法では不要な再帰的処理を避ける事が出来る。既に行った計算結果を保持しているソースコードを抽出せよ。
A：

python

# 誤差逆伝播
def backward(x, d, z1, y):
    print("\n##### 誤差逆伝播開始 #####")

    grad = {}

    W1, W2 = network['W1'], network['W2']
    b1, b2 = network['b1'], network['b2']
    #  出力層でのデルタ
    delta2 = functions.d_sigmoid_with_loss(d, y)
    #  b2の勾配
    grad['b2'] = np.sum(delta2, axis=0)
    #  W2の勾配
    grad['W2'] = np.dot(z1.T, delta2)
    #  中間層でのデルタ
    delta1 = np.dot(delta2, W2.T) * functions.d_relu(z1)
    # b1の勾配
    grad['b1'] = np.sum(delta1, axis=0)
    #  W1の勾配
    grad['W1'] = np.dot(x.T, delta1)
        
    print_vec("偏微分_dE/du2", delta2)
    print_vec("偏微分_dE/du2", delta1)

    print_vec("偏微分_重み1", grad["W1"])
    print_vec("偏微分_重み2", grad["W2"])
    print_vec("偏微分_バイアス1", grad["b1"])
    print_vec("偏微分_バイアス2", grad["b2"])

    return grad

【P83】
**Q：**2つの空欄に該当するソースコードを探せ
(1) $\frac{\partial E}{\partial y}\frac{\partial y}{\partial u}$
(2) $\frac{\partial E}{\partial y}\frac{\partial y}{\partial u}\frac{\partial u}{\partial w_{ji}^{(2)}}$
A：
(1)

  #  出力層でのデルタ
    delta2 = functions.d_mean_squared_error(d, y)

(2)

   # W2の勾配
    grad['W2'] = np.dot(z1.T, delta2)

３．実装演習

###順伝番とネットワーク構成
(ファイル名：1_1_forward_propagation.ipynb)
####【実装結果】
https://github.com/HienDT27/Rabbit-Challenge/blob/master/%E3%80%90%E6%B7%B1%E5%B1%A4%E5%AD%A6%E7%BF%92_Day_01%E3%80%911_1_forward_propagation.ipynb
####【考察】
　●　Pythonのライブラリ「Numpy」で、ネットワークの初期化（重み、バイアスなど）またはネットワークの構成（中間層の数など）を設定することができる。
　●　学習モデルの精度向上ために、中間層において、層の数、各層のノード数の決定が難しいと思った。
###誤差逆伝番法
(ファイル名：1_2_back_propagation.ipynb)
####【実装結果】
https://github.com/HienDT27/Rabbit-Challenge/blob/master/%E3%80%90%E6%B7%B1%E5%B1%A4%E5%AD%A6%E7%BF%92_Day_01%E3%80%911_2_back_propagation.ipynb
####【考察】
　●　誤差逆伝播にて毎ステップに各層の重み、バイアスの値を更新され、誤差関数の値を減らすことができる。（良いパラメータを決定できる）
実装結果より、重みやバイアスを一回更新すると、誤差を　0.091　➡　0.087に減らした。
　●　学習率を10倍にすると、誤差逆伝播後の誤差も小さくなることが分かった。
（誤差を　0.091　➡　0.057）
###勾配降下法
(ファイル名：1_3_stochastic_gradient_descent.ipynb)
####【実装結果】
https://github.com/HienDT27/Rabbit-Challenge/blob/master/%E3%80%90%E6%B7%B1%E5%B1%A4%E5%AD%A6%E7%BF%92_Day_01%E3%80%911_3_stochastic_gradient_descent.ipynb
####【考察】
　●　活性化関数の変更（ReLU➡Sigmoid）より、最初のepochでも誤差が０に近い。
　●　データにおける x の範囲を変更した場合、モデルの収束に大きな影響が与える。

４．修了課題

###①課題設定
Irisデータセットを用いて、Deep Neural Network ( DNN)を作成し、回帰問題や分類問題を解く
###➁課題設計・実装結果
Irisデータとは、機械学習でよく使われるアヤメの品種のデータです。アヤメの品種のSetosa ,Versicolor, Virginicaの3品種に関する150件のデータが入っています。
データセットの中身はSepal Length（がく片の長さ）、Sepal Width（がく片の幅）、Petal Length（花びらの長さ）、Petal Width（花びらの幅）の4つの特徴量を持っています。
####【ネットワーク構成設計】：３クラス分類問題
■　ネットワーク構成
　●　入力層：４ノード（それぞれの4つの特徴量を示す）
　●　隠れ層：1層（１０ノード）
　●　出力層:３ノード
　●　入力層➡隠れ層の活性化関数：ReLU関数
　●　隠れ層➡出力層の活性化関数：Softmax関数
　●　損失関数：交差エントロピー誤差を利用する
　●　パラメータを誤差逆伝播より更新される
■　分類問題解決案
　●　Irisデータを学習データとテストデータに分割する
　●　学習データに対して、毎epoch後に誤差逆伝播法よりパラメータが更新される
　●　学習工程が完了後、得られた重みとバイアス（パラメータ）を利用して、テストデータにて誤差と正答率で評価する
　●　今回には、学習率または学習データとテストデータの分割比例よりモデル精度を評価してみる。
####【実装結果】
https://github.com/HienDT27/Rabbit-Challenge/blob/master/%E3%80%90%E6%B7%B1%E5%B1%A4%E5%AD%A6%E7%BF%92_Day_01%E3%80%91%E3%80%90%E4%BF%AE%E4%BA%86%E8%AA%B2%E9%A1%8C%E3%80%91Iris_Dataset.ipynb
####【考察】
■　分割率（学習：テスト➡7：3）、学習率：0.07の場合の正答率：

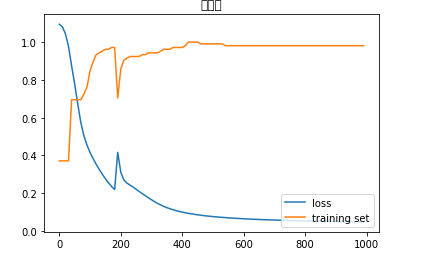
　●　学習：　正答率　➡　0.9809523809523809
　●　テスト：正答率　➡　0.9555555555555556　　　　
■　分割率（学習：テスト➡7：3）、学習率：0.01の場合の正答率：

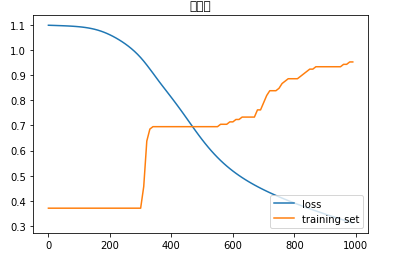
　●　学習：　正答率　➡　0.9523809523809523　　　　　
　●　テスト：正答率　➡　0.8888888888888888
学習率が低くなると、学習に時間がかかることが分かった。
■　分割率（学習：テスト➡2：8）、学習率：0.07の場合の正答率：

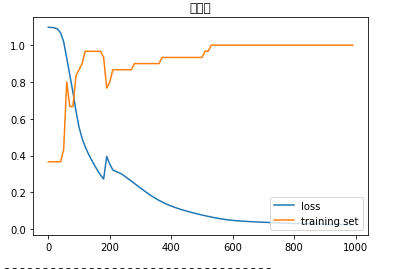
　●　学習：　正答率　➡　1.0　　　　　
　●　テスト：正答率　➡　0.9166666666666666
学習データが少ないと最適なパラメータの値を得られないので、テスト評価に影響が与える（テストの正答率が小さくなる）