以下の関数の定義から出発します。
【Python演算処理】冪算と乗除算の関係について。
二つの数の集合X,Yがあって、Xの要素xに対してYの要素yがただ一つ定まる時、この対応を関数(Function)と呼びy=f(x)などと書き表す(fはfunctionの略だが、複数の関数への言及が不可避となる状況ではそれをy=g(x),y=h(x)などと呼び分ける)。
- この時xを独立変数(Independent Variable)、yを従属変数(Dependent Variable)と呼ぶ。
- また集合Xを関数fの定義域(Domain)、集合Yの部分集合$(y|y=f(x),x \in X)$をこの関数の値域(Range)という。
関数y=fxの変化の様子はxの値を横座標、yの値を縦座標としxを定義域内で変化させた時の点P(x,y)の軌跡を描くと一目瞭然となる。これが関数y=f(x)のグラフである。
正直言って高校までの数学においては微分(Differential)は事実上以下の公式の暗記と再生に過ぎませんでした。
微分計算は素直。積分計算は超エキサイティング。初等関数(三角関数や指数関数など)の四則演算や合成で表現できる関数は,基本的な公式を組み合わせるだけで必ず微分できます(一方,不定積分は必ずしも初等関数で表せるとは限らない)。
基本演算
①線形性
$(kf(x))'=kf'(x)$(ただしkは定数=スカラー倍の概念に対応)
$(af(x)±bg(x))'=af'(x)±bg'(x)$
高校数学における線形性の8つの例 | 高校数学の美しい物語
別の記法ではこうなる。
\frac{d}{dt}(kX(t))=k\frac{d}{dt}X(t)\\
\frac{d}{dt}(aX(t)±bY(t))=a\frac{d}{dt}X(t)±b\frac{d}{dt}Y(t)
②積の微分:
$(fg)'=f'g+fg'$
積の微分公式とその証明の味わい
**【例題】**関数$y=f(x)=x^2$と関数$y=g(x)=\sin(x)$の積の微分。
\frac{dy}{dx}x^2=2x\\
\frac{dy}{dx}\sin(x)=\cos(x)
よって積の微分公式f'g+fg'に従って
f'g+fg'=2x \sin(x)+x^2 \cos(x)
pythonによる実装結果
import sympy as sp
x,y = sp.symbols('x,y')
# 原始関数
f=x**2*sp.sin(x)
# 微分
g=sp.diff(f,x,1)
# 積分
h=sp.integrate(g,x)
# 画面表示
sp.init_printing()
display(f)
print(sp.latex(f))
display(g)
print(sp.latex(g))
display(h)
print(sp.latex(h))
原始関数
x^{2} \sin{\left(x \right)}
微分結果
x^{2} \cos{\left(x \right)} + 2 x \sin{\left(x \right)}
積分による復元
x^{2} \sin{\left(x \right)}
③商の微分(分数の微分):
$(\frac{g}{f})'=\frac{g'f-f'g}{f^2}$
商の微分公式の証明と例題
【例題】$y=f(x)=\frac{\cos (x)}{\sin (x)}$の微分
\frac{dy}{dx}\cos(x)=-\sin(x)\\
\frac{dy}{dx}\sin(x)=\cos(x)\\
\cos^2(x)+\sin^2(x)=1
よって商の微分公式$\frac{g'f-f'g}{f^2}$に従って
y'=\frac{\cos(x)'sin(x)-\sin(x)'\cos(x)}{\sin^2(x)}\\
= \frac{-\sin^2(x)-\cos^2(x)}{\sin^2(x)}\\
= -\frac{1}{\sin^2(x)}
pythonによる実装結果
import sympy as sp
x,y = sp.symbols('x,y')
# 原始関数
f=sp.cos(x)/sp.sin(x)
# 微分
g=sp.diff(f,x,1)
# 積分
h=sp.integrate(g,x)
# 画面表示
sp.init_printing()
display(f)
print(sp.latex(f))
display(g)
print(sp.latex(g))
display(h)
print(sp.latex(h))
原始関数
\frac{\cos{\left(x \right)}}{\sin{\left(x \right)}}
微分結果
-1 - \frac{\cos^{2}{\left(x \right)}}{\sin^{2}{\left(x \right)}}
積分による復元
\frac{\cos{\left(x \right)}}{\sin{\left(x \right)}}
まぁSympyの癖も分かってきたので、別にこの程度では驚きません。逆をいえば「ここでピタゴラスの定理の導入を確実に思いつく」のが人工知能とも?
- 特にg=1の時,$(\frac{1}{f})'=-\frac{f'}{f^2}$(逆数の微分)
【例題】$\frac{1}{log(x)}$の微分
\frac{dy}{dx}\log(x)=\frac{1}{x}
よって逆数の微分公式$-\frac{f'}{f^2}$に従って
y'=-\frac{\log(x)'}{\log(x)^2}=-\frac{1}{x(\log(x)^2}
pythonによる実装結果
import sympy as sp
x,y = sp.symbols('x,y')
# 原始関数
f=1/sp.log(x)
# 微分
g=sp.diff(f,x,1)
# 積分
h=sp.integrate(g,x)
# 画面表示
sp.init_printing()
display(f)
print(sp.latex(f))
display(g)
print(sp.latex(g))
display(h)
print(sp.latex(h))
原始関数
\frac{1}{\log{\left(x \right)}}
微分結果
- \frac{1}{x \log{\left(x \right)}^{2}}
積分による復元
\frac{1}{\log{\left(x \right)}}
④合成関数の微分:
$(f(g(x))'=f'(g(x))g'(x)$
合成関数の微分公式と例題7問
別の記法ではこうなる。
y=f(u)がuについて微分可能であり、かつu=g(x)がxについて微分可能であれば、合成関数y=f(g(x))はxについて微分可能であり$\frac{dy}{dx}=\frac{dy}{du}\frac{du}{dx}$と表される。
**【例題】**関数$y=(5x+3)^2$の微分
y=f(u)=u^2…①\\
u=g(x)=5x+3…②
この時、yは以下の形でxの関数となる。
y=f(u)=u^2=(5x+3)^2…③
逆をいえば$y=(5x+3)^2$の式について$u=5x+3$と置いたのが①②ともいえる。③を展開して項別にxで微分すれば導関数が得られるが、③は①②の合成関数なので以下となる。
\frac{dy}{dx}=\frac{dy}{du}\frac{du}{dx}\\
\frac{dy}{du}u^2=2u\\
\frac{du}{dx}5x+3=5\\
\frac{dy}{du}\frac{du}{dx}=2u*5=10u=10(5x+3)=50x+30
pythonによる実装結果
import sympy as sp
x,y = sp.symbols('x,y')
# 原始関数
f=(5*x+3)**2
# 微分
g=sp.diff(f,x,1)
# 積分
h=sp.integrate(g,x)
# 画面表示
sp.init_printing()
display(f)
print(sp.latex(f))
display(g)
print(sp.latex(g))
display(h)
print(sp.latex(h))
原始関数
\left(5 x + 3\right)^{2}
微分結果
50 x + 30
積分による復元
25 x^{2} + 30 x
合成微分には積分による復元性に難がある?
【例題】$\cos(ax+b)$の微分
$y=\cos(u),u=ax+b$と置く。
\frac{dy}{dx}\cos(x)=-\sin(x)\\
よって合成関数の微分公式に従い
\frac{dy}{dx}=\frac{dy}{du}\frac{du}{dx}\\
\frac{dy}{du}cos(x)=-sin(u)\\
\frac{du}{dx}ax+b=a\\
\frac{dy}{du}\frac{du}{dx}=a(-\sin(u))=-a(\sin(ax+b))
pythonによる実装結果
import sympy as sp
x,a,b = sp.symbols('x,a,b')
# 原始関数
f=sp.cos(a*x+b)
# 微分
g=sp.diff(f,x,1)
# 積分
h=sp.integrate(g,x)
# 画面表示
sp.init_printing()
display(f)
print(sp.latex(f))
display(g)
print(sp.latex(g))
display(h)
print(sp.latex(h))
原始関数
\cos{\left(a x + b \right)}
微分結果
- a \sin{\left(a x + b \right)}
積分による復元
- a \left(\begin{cases} - \frac{\cos{\left(a x + b \right)}}{a} & \text{for}\: a \neq 0 \\x \sin{\left(b \right)} & \text{otherwise} \end{cases}\right)
やはり合成微分には積分による復元性に難がある?
【例題】$e^{ax}$の微分
$y=e^u,u=ax$と置く。
\frac{dy}{dx}e^x=e^x\\
よって合成関数の微分公式に従い
\frac{dy}{dx}=\frac{dy}{du}\frac{du}{dx}\\
\frac{dy}{du}e^u=-e^u\\
\frac{du}{dx}ax=a\\
\frac{dy}{du}\frac{du}{dx}=a(e^u)=-ae^{ax}
pythonによる実装結果
import sympy as sp
x,a= sp.symbols('x,a')
# 原始関数
f=sp.exp(a*x)
# 微分
g=sp.diff(f,x,1)
# 積分
h=sp.integrate(g,x)
# 画面表示
sp.init_printing()
display(f)
print(sp.latex(f))
display(g)
print(sp.latex(g))
display(h)
print(sp.latex(h))
原始関数
e^{a x}
微分結果
a e^{a x}
積分による復元
e^{a x}
⑤(公式ではないが)対数微分法
- 「両辺>0」を確認して対数を取る(正でないときは絶対値を取る)
- 両辺を x で微分する
- y'について解く
対数微分法のやり方と例題
【例題】$y=x^x$の微分。
$y=x^x$の指数の底は正なので,そもそも関数の定義域がx>0xであることに注意する。よって,両辺は正なのでそのまま対数を取れる:
\log(y)=xlog(x)
両辺をxで微分する。左辺は前提知識で述べた公式,右辺は積の微分の公式を使う:
\frac{y'}{y}=log(x)+1
これを y'について解く:
y'=y(\log(x)+1)
yをもとに戻す:
y'=x^x(\log(x)+1)
pythonによる実装結果
import sympy as sp
x= sp.symbols('x')
# 原始関数
f=x**x
# 微分
g=sp.diff(f,x,1)
# 積分
h=sp.integrate(g,x)
# 画面表示
sp.init_printing()
display(f)
print(sp.latex(f))
display(g)
print(sp.latex(g))
display(h)
print(sp.latex(h))
原始関数
x^{x}
微分結果
x^{x} \left(\log{\left(x \right)} + 1\right)
積分による復元
x^{x}
Sympy、こういうのはケロっとこなすのでかえってその考え方の重要性を見逃す契機になってしまう?
冪関数の微分
(x^{α})'=αx^{α-1}(αは任意の実数)
- 例えば$(x^2)'=2x,(x^{10})'=9x^9$
対応する以下の積分公式がα-1の時に使えない。
\int x^α dx=\frac{1}{α+1}x^{α+1}+C(α \in \mathbb{R} \land α \neq -1)
それで以下の式で代用する事が多い。
(α^x)'=α^x \log(α)\\
\int α^x dx = \frac{α^x}{\log(α)}
- α=−1とすると$(\frac{1}{x})'=-\frac{1}{x^2}$
pythonによる実装結果
import sympy as sp
x= sp.symbols('x')
# 原始関数
f=1/x
# 微分
g=sp.diff(f,x,1)
g2=sp.diff(f,x,2)
# 積分
h=sp.integrate(g,x)
# 画面表示
sp.init_printing()
display(f)
print(sp.latex(f))
display(g)
print(sp.latex(g))
display(h)
print(sp.latex(h))
display(g2)
print(sp.latex(g2))
原始関数
\frac{1}{x}
微分結果
- \frac{1}{x^{2}}
積分による復元
\frac{1}{x}
二階微分だと負号が消える
\frac{2}{x^{3}}
- α=$\frac{1}{2}$とすると$(\sqrt{x})'=\frac{1}{2\sqrt{x}}$
pythonによる実装結果
import sympy as sp
x= sp.symbols('x')
# 原始関数
f=sp.sqrt(x)
# 微分
g=sp.diff(f,x,1)
# 積分
h=sp.integrate(g,x)
# 画面表示
sp.init_printing()
display(f)
print(sp.latex(f))
display(g)
print(sp.latex(g))
display(h)
print(sp.latex(h))
原始関数
\sqrt{x}
微分結果
\frac{1}{2 \sqrt{x}}
積分による復元
\sqrt{x}
この演算は「同心円集合$r^{\frac{1}{2}}$に内接/外接する正方形集合」と縁深い事で知られている。
指数対数関数の微分
微積分演算に対応しない形で以下の観測結果集合を構成する。
【初心者向け】指数・対数関数の発見とそれ以降の発展について。

| 自然指数関数 | 自然対数関数 | |
|---|---|---|
| 0 | y=exp(x) | y=log(x) |
| 1 | y=exp(-x) | y=log(-x) |
| 2 | y=-exp(x) | y=-log(x) |
| 3 | y=-exp(-x) | y=-log(-x) |
- $(e^x)'=e^x$…積分の結果も$\int e^x dx = e^x$となる。
- $(e^{ax})'=ae^{ax}$…積分の結果は$\int e^{ax} dx = \frac{1}{a}e^{ax}$となる。
- $(\log(x))'=\frac{1}{x}$…これに対応する積分の結果は$\int \frac{1}{x} dx = \log(x)$となる。
- $(\log_{a}(x))'=\frac{1}{x \log(a)}$…一般の対数関数の場合。
- $(α^x)'=α^x \log(α)$…用例は上掲。
【数理考古学】冪乗算の微積分
これに関連して
\int \log(x) dx = x(log(x)-1)+C
pythonによる実装結果
import sympy as sp
x,a= sp.symbols('x,a')
# 原始関数
f=sp.log(x)
# 微分
g=sp.integrate(f,x)
# 積分
h=sp.diff(g,x,1)
# 画面表示
sp.init_printing()
display(f)
print(sp.latex(f))
display(g)
print(sp.latex(g))
display(h)
print(sp.latex(h))
原始関数
\log{\left(x \right)}
積分結果
x \log{\left(x \right)} - x
微分による復元
\log{\left(x \right)}
そして虚冪演算の微積分は回転を通じて三角関数に関連付けられます。
【Python演算処理】冪算と乗除算の関係について。
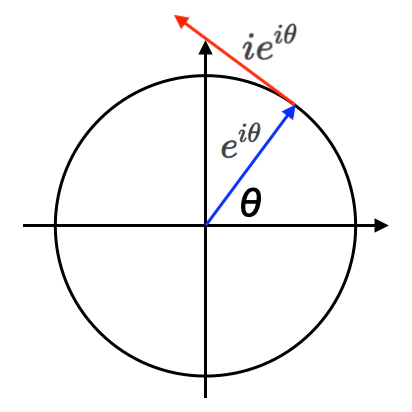
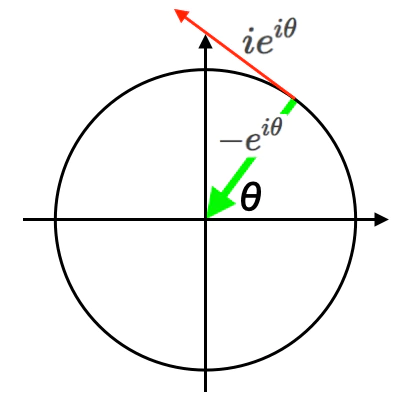
- $e^{ix}\frac{d^n}{dθ^n}=(i e^{i x}(-\log ix),-e^{ix},-i e^{i x}(\log ix),e^{ix},…)$
- $\int \int \int … \int e^{ix}(dθ)=(- i e^{i x}(\log ix),- e^{i x},i e^{i x}(-\log ix),e^{ix},…)$
さてドン尻に控えしは…
- $(\log(x+\sqrt{x^2+a}))'=\frac{1}{\sqrt{x^2+a}}$…何に用いられる式か不明だが、大学受験の出題範囲に入っているっぽくてネットに解答例が頻出。
pythonによる実装結果
import sympy as sp
x,a= sp.symbols('x,a')
# 原始関数
f=sp.log(x+sp.sqrt(x**2+a))
# 微分
g=sp.diff(f,x,1)
# 積分
h=sp.integrate(g,x)
# 画面表示
sp.init_printing()
display(f)
print(sp.latex(f))
display(g)
print(sp.latex(g))
display(h)
print(sp.latex(h))
原始関数
\log{\left(x + \sqrt{a + x^{2}} \right)}
微分結果
\frac{\frac{x}{\sqrt{a + x^{2}}} + 1}{x + \sqrt{a + x^{2}}}
積分による復元
\log{\left(x + \sqrt{a + x^{2}} \right)}
Sympy完全に猫跨ぎ…微塵のモチベーションも感じられません。この猫っぽい仕草が本当に愛らしいのですよ。
三角関数の微分
三角関数の微分(それぞれが+90度の変遷に対応)
\cos(θ)\frac{d^n}{dθ^n}=(-\sin(θ),-\cos(θ),\sin(θ),\cos(θ),…)\\
\sin(θ)\frac{d^n}{dθ^n}=(\cos(θ),-\sin(θ),-\cos(θ),\sin(θ),…)
三角関数の積分(それぞれが-90度の変遷に対応)
\int \int \int … \int \cos(θ)(dθ)=(\sin(θ),-\cos(θ),-\sin(θ),\cos(θ),…)\\
\int \int \int … \int \sin(θ)(dθ)=(-\cos(θ),-\sin(θ),\cos(θ),\sin(θ),…)
【Python演算処理】等速円運動についての物理学と数学の立場の違い?
- $\cos(θ)=\frac{e^{θi}+e^{-θi}}{2}$
- $\sin(θ)=\frac{e^{θi}-e^{-θi}}{2i}$
- $(\tan x)'=\frac{1}{\cos^2(x)}$…タンジェントの微分結果
pythonによる実装結果
import sympy as sp
x,a= sp.symbols('x,a')
# 原始関数
f=sp.tan(x)
# 微分
g=sp.diff(f,x,1)
# 積分
h=sp.integrate(g,x)
# 画面表示
sp.init_printing()
display(f)
print(sp.latex(f))
display(g)
print(sp.latex(g))
display(h)
print(sp.latex(h))
原始関数
\tan{\left(x \right)}
微分結果
\tan^{2}{\left(x \right)} + 1
積分による復元
\frac{\sin{\left(x \right)}}{\cos{\left(x \right)}}
Sympy「にゃー(タンジェントなんてオワコン)」圧を感じます。
- $(\cot x)'=(\frac{1}{\tan(x)})'=-\frac{1}{\sin^2(x)}$…コタンジェント(タンジェントの逆数)の微分結果
pythonによる実装結果
import sympy as sp
x,a= sp.symbols('x,a')
# 原始関数
f=sp.cot(x)
# 微分
g=sp.diff(f,x,1)
# 積分
h=sp.integrate(g,x)
# 画面表示
sp.init_printing()
display(f)
print(sp.latex(f))
display(g)
print(sp.latex(g))
display(h)
print(sp.latex(h))
原始関数
\cot{\left(x \right)}
微分結果
- \cot^{2}{\left(x \right)} - 1
積分による復元
\frac{\cos{\left(x \right)}}{\sin{\left(x \right)}}
Sympy「にゃー(コタンジェントなんてオワコン)」圧を感じます。
三角関数 - Wikipedia

三角関数のグラフ: Sine(青実線)、 Cosine(緑実線)、 Tangent(赤実線)、 Cosecant(青点線)、 Secant(緑点線)、 Cotangent(赤点線)
- $(\mathrm{Arcsin}(x))′=\frac{1}{\sqrt{1-x^2}}$
pythonによる実装結果
import sympy as sp
x,a= sp.symbols('x,a')
# 原始関数
f=sp.asin(x)
# 微分
g=sp.diff(f,x,1)
# 積分
h=sp.integrate(g,x)
# 画面表示
sp.init_printing()
display(f)
print(sp.latex(f))
display(g)
print(sp.latex(g))
display(h)
print(sp.latex(h))
原始関数
\operatorname{asin}{\left(x \right)}
微分結果
\frac{1}{\sqrt{1 - x^{2}}}
積分による復元
\operatorname{asin}{\left(x \right)}
- $(\mathrm{Arccos}(x))'=-\frac{1}{\sqrt{1-x^2}}$
pythonによる実装結果
import sympy as sp
x,a= sp.symbols('x,a')
# 原始関数
f=sp.acos(x)
# 微分
g=sp.diff(f,x,1)
# 積分
h=sp.integrate(g,x)
# 画面表示
sp.init_printing()
display(f)
print(sp.latex(f))
display(g)
print(sp.latex(g))
display(h)
print(sp.latex(h))
原始関数
\operatorname{acos}{\left(x \right)}
微分結果
- \frac{1}{\sqrt{1 - x^{2}}}
積分による復元
\operatorname{acos}{\left(x \right)}
- $(\mathrm{Arctan}(x))'=\frac{1}{1+x^2}$
pythonによる実装結果
import sympy as sp
x,a= sp.symbols('x,a')
# 原始関数
f=sp.atan(x)
# 微分
g=sp.diff(f,x,1)
# 積分
h=sp.integrate(g,x)
# 画面表示
sp.init_printing()
display(f)
print(sp.latex(f))
display(g)
print(sp.latex(g))
display(h)
print(sp.latex(h))
原始関数
\operatorname{atan}{\left(x \right)}
微分結果
\frac{1}{x^{2} + 1}
積分による復元
\operatorname{atan}{\left(x \right)}
- $(\mathrm{Arccot}(x))'=-\frac{1}{1+x^2}$
pythonによる実装結果
import sympy as sp
x,a= sp.symbols('x,a')
# 原始関数
f=sp.acot(x)
# 微分
g=sp.diff(f,x,1)
# 積分
h=sp.integrate(g,x)
# 画面表示
sp.init_printing()
display(f)
print(sp.latex(f))
display(g)
print(sp.latex(g))
display(h)
print(sp.latex(h))
原始関数
\operatorname{acot}{\left(x \right)}
微分結果
-\frac{1}{x^{2} + 1}
積分による復元
\operatorname{acot}{\left(x \right)}
逆三角関数 - Wikipedia

平面上の直交座標系で図示されたarcsin(x)(赤)と arccos(x)(青)の通常の定義における主値。

平面上の直交座標系で図示されたarctan(x)(赤)と arccot(x) (青)の通常の定義における主値。
- $(\sinh(x))'=\cosh(x)$
pythonによる実装結果
import sympy as sp
x,a= sp.symbols('x,a')
# 原始関数
f=sp.sinh(x)
# 微分
g=sp.diff(f,x,1)
# 積分
h=sp.integrate(g,x)
# 画面表示
sp.init_printing()
display(f)
print(sp.latex(f))
display(g)
print(sp.latex(g))
display(h)
print(sp.latex(h))
原始関数
\sinh{\left(x \right)}
微分結果
\cosh{\left(x \right)}
積分による復元
\sinh{\left(x \right)}
- $(\cosh x)'=\sinh(x)$
pythonによる実装結果
import sympy as sp
x,a= sp.symbols('x,a')
# 原始関数
f=sp.cosh(x)
# 微分
g=sp.diff(f,x,1)
# 積分
h=sp.integrate(g,x)
# 画面表示
sp.init_printing()
display(f)
print(sp.latex(f))
display(g)
print(sp.latex(g))
display(h)
print(sp.latex(h))
原始関数
\cosh{\left(x \right)}
微分結果
\sinh{\left(x \right)}
積分による復元
\cosh{\left(x \right)}
- $(\tanh x)'=1-\tanh^2(x)$
pythonによる実装結果
import sympy as sp
x,a= sp.symbols('x,a')
# 原始関数
f=sp.tanh(x)
# 微分
g=sp.diff(f,x,1)
# 積分
h=sp.integrate(g,x)
# 画面表示
sp.init_printing()
display(f)
print(sp.latex(f))
display(g)
print(sp.latex(g))
display(h)
print(sp.latex(h))
原始関数
\tanh{\left(x \right)}
微分結果
1 - \tanh^{2}{\left(x \right)}
積分による復元
\tanh{\left(x \right)}
そして受験数学ではほとんど黙殺されているに等しいこの双曲線関数こそが機械学習概念の発端となったシグモイド曲線へとつながっていくのです。
【Python演算処理】冪算と乗除算の関係について。
{{\displaystyle \varsigma _{a}(x)={\frac {1}{1+e^{-ax}}}={\frac {\tanh(ax/2)+1}{2}}}
}
円と球を巡る微積分
【Python演算処理】半径・直径・円周長・円の面積・球の表面積・球の体積の計算上の往復
【Python演算処理】「N次球概念導入による円/球関係の数理の統合」?
- 円の面積$πr^2$$を半径rで微分すると円周の長さ2πrとなる。逆に円周の長さ2πrを半径rで積分すると円の面積$πr^2$になる。
- 球の体積$4/3πr^3$を半径rで微分すると球の表面積$4πr^2$、逆に球の表面積$4πr^2$を半径rで積分すると球の体積$4/3πr^3$となる。
- 球の表面積$4πr^2$を半径rで微分すると円周長2πr、逆に円周長2πrを半径rで積分すると球の表面積$4πr^2$となる。
どうして微積分可能範囲がこんな形で「離散的」に現れるのか。それを説明するには階乗の概念を複素数全体に拡張したΓ関数の導入を必要不可欠とする。要するにこれらはそれぞれ構造全体を説明する巨大な単一方程式の部分抽出に過ぎないのである。
これで概ね大学受験数学までに習う微分の範囲は網羅した? とはいえ、これらの知識を総動員したとしても「微分とは何か」自体はまるで見えてきません。それを理解するにはまた別のアプローチが必要となる様なのです。
微分とは何か?(理論編)
関数y=f(x)の定義域(x)内の点αにおいて$Δx \to 0$の時、$\frac{f(α+Δx)-f(α)}{Δx}$が一定の値に収束する時「関数y=f(x)はx=αで微分可能である」とし、この一定の値をx=aにおける微分係数と呼びf'(α)で表す。
f'(a)=\lim_{Δx \to 0}\frac{f(α+Δx)-f(α)}{Δx}
- Δx→0はΔx>0から0に近づけても、Δx<0から0に近づけても、また正負を交互に変化させつつ0に近づけても良い。いずれにせよα+Δxの数直線上の絶対値がαに漸近する事が重要なのである。
関数f(x)がx=aの十分近くで定義されている時、Δy=f(a+Δx)-f(a)だとすると$\frac{Δy}{Δx}=\frac{f(a+Δx)-f(a)}{Δx}$は関数f(x)上の2点a,bを通る直線lの傾きを表す。すなわち「x=αで微分可能である」という事は、点a,bを限りなく近づけた時直線lの傾きが一定に近づく一点が存在する事を意味する。すなわち点A(a,f(a))(あるいは点B(b,f(b)))付近のグラフが滑らかで連続しておりドンドン拡大していくと直線とみなせる状態に到達する、すなわち「拡大して直線と見做せた時に微分可能と見做され、その時の直線の傾きが微分係数となる」のである。
\lim_{Δx \to 0}\frac{Δy}{Δx}=\lim_{Δx \to 0}\frac{f(α+Δx)-f(α)}{Δx}
- ここで導入された「十分に近い」概念はおそらく抽象数学における「近傍(Neighbourhood)」概念と密接に関係している。
近傍とは - コトバンク
ここで集合x=(a,b,c,…)にその微分係数(f'(a),f'(b),f'(c),…)を対応させる関数f'(x)を考え、原始関数(Primitive Function)f(x)の導関数(Derivative Function)と呼ぶ事にする。
f'(x)=\lim_{Δx \to 0}\frac{Δy}{Δx}=\lim_{Δx \to 0}\frac{f(x+Δx)-f(x)}{Δx}
導関数の記号は$y',\frac{dy}{dx},\frac{dy}{dx}f(x)$などでも良い。いずれにせよ関数f(x)の導関数を求める事を「微分する」と呼ぶ。
何だか分かるような分からない様な抽象的な定義ですね。しかしまぁ、ある意味それこそが厳密さを極めた現代数学の特徴とも? そして…
高校数学からヤコビアンに至るまで
- 「合成関数の微分」概念は最小単位Δを共有する「チェーンメール変換」イメージを経て偏微分方程式の各変数を関数とする多重積分に拡張される。
- さらにここでいう共通最小単位Δの定義がイプシロンデルタ論法によって拡張される。
- こうして強化された共通最小単位Δの概念を直交座標と極座標の変換に導入した結果がヤコビアン行列となる。

大雑把にいうとこうした考え方が大学で習う「専門数学」の領域に入ってくる様です。まだまだ全体像は掴めないままですが、何となく道筋は掴めてきた感じがします。
- これまでの投稿で述べてきた 「同心集合(Concentric Set)=中心0の1点でのみ固定された数直線上に置かれたそれぞれの値が描く同心円/同心球面t」概念自体がここに登場しないのは、「空間全体を構成する偏微分方程式を各変数ごとの多重積分に変換する過程」においては、まず半径r=スカラー量を抽出し、しかるのちに一次トーラス=半径1の単位円(円周長2π)の直積によって全体を把握していくのが直交座標(r(スカラー量),φ(-π~+π),θ(-π~+π),…)の流儀だから。
- もちろんこの考え方だけでは「メルカトル座標系(φ=-π~+π,θ=0~π)と二次元トーラス座標系(φ=-π~+π,θ=-π~+π)」「ヤコビアン座標系(r=0~1,φ=-π~+π,θ=0~π)と三次元トーラス(四元数)座標系(i,j,kそれぞれが-1~+1の稼働範囲)」それぞれのメリットとデメリットが上手く説明出来ず、これからの克服課題として急浮上してくる。
現時点での自認は大体こんな感じ?
微分とは何か?(実践編)
導関数がX軸とY軸の間に間に作る面積は原始関数の値と一致する。
改めて具体的に「微分とは何か?」再掌握するには、この辺りが鍵となってくる様です。
一次方程式y=x
y=x\\
y'=1
導関数の導出過程
f'(x)=\lim_{Δx \to 0}\frac{Δy}{Δx}=\lim_{Δx \to 0}\frac{f(x+Δx)-f(x)}{Δx}\\
=\lim_{Δx \to 0}\frac{(x+Δx)-x}{Δx}=\lim_{Δx \to 0}\frac{Δx}{Δx}=1
x=4の時、原始関数y=x→y=4、導関数y=1→y=1×4=4

二次方程式y=x^2
y=\frac{1}{2}x^2 \\
y'=x
導関数の導出過程
f'(x)=\lim_{Δx \to 0}\frac{Δy}{Δx}=\lim_{Δx \to 0}\frac{f(x+Δx)-f(x)}{Δx}\\
=\lim_{Δx \to 0}\frac{(x+Δx)^2-x^2}{Δx}\\
=\lim_{Δx \to 0}\frac{(x^2+2xΔx+Δx^2)-x^2}{Δx}\\
=\lim_{Δx \to 0}\frac{2xΔx+Δx^2}{Δx}\\
=\lim_{Δx \to 0}2x+Δx=2x
【参考】二次形式行列における「マスキング」
import sympy as sp
a,b = sp.symbols('a,b')
# Rows
x=sp.Matrix([[a,1]])
# Columns
y=sp.Matrix([[a],[1]])
a00=sp.Matrix([[1,1],[1,1]])
a11=sp.Matrix([[1,0],[0,0]])
a12=sp.Matrix([[0,1],[0,0]])
a21=sp.Matrix([[0,0],[1,0]])
a22=sp.Matrix([[0,0],[0,1]])
adp=sp.Matrix([[1,0],[0,1]])
adm=sp.Matrix([[0,1],[1,0]])
sp.init_printing()
display(x)
display(a00)
display(a11)
display(a12)
display(a21)
display(a22)
display(adp)
display(adm)
display(y)
display(sp.simplify(x*a00*y))
print(sp.latex(x)+sp.latex(a00)+sp.latex(y)+"="+sp.latex(sp.simplify(x*a00*y)))
display(sp.simplify(x*a11*y))
print(sp.latex(x)+sp.latex(a11)+sp.latex(y)+"="+sp.latex(sp.simplify(x*a11*y)))
display(sp.simplify(x*a12*y))
print(sp.latex(x)+sp.latex(a12)+sp.latex(y)+"="+sp.latex(sp.simplify(x*a12*y)))
display(sp.simplify(x*a21*y))
print(sp.latex(x)+sp.latex(a21)+sp.latex(y)+"="+sp.latex(sp.simplify(x*a21*y)))
display(sp.simplify(x*a22*y))
print(sp.latex(x)+sp.latex(a22)+sp.latex(y)+"="+sp.latex(sp.simplify(x*a22*y)))
display(sp.simplify(x*adp*y))
print(sp.latex(x)+sp.latex(adp)+sp.latex(y)+"="+sp.latex(sp.simplify(x*adp*y)))
display(sp.simplify(x*adm*y))
print(sp.latex(x)+sp.latex(adm)+sp.latex(y)+"="+sp.latex(sp.simplify(x*adm*y)))
\left[\begin{matrix}a & 1\end{matrix}\right]\left[\begin{matrix}1 & 1\\1 & 1\end{matrix}\right]\left[\begin{matrix}a\\1\end{matrix}\right]=\left[\begin{matrix}a \left(a + 1\right) + a + 1\end{matrix}\right]\\=[a^2+2a+1]=[(a+1)^2]…①\\
\left[\begin{matrix}a & 1\end{matrix}\right]\left[\begin{matrix}1 & 0\\0 & 0\end{matrix}\right]\left[\begin{matrix}a\\1\end{matrix}\right]=\left[\begin{matrix}a^{2}\end{matrix}\right]…②\\
\left[\begin{matrix}a & 1\end{matrix}\right]\left[\begin{matrix}0 & 1\\0 & 0\end{matrix}\right]\left[\begin{matrix}a\\1\end{matrix}\right]=\left[\begin{matrix}a\end{matrix}\right]…③\\
\left[\begin{matrix}a & 1\end{matrix}\right]\left[\begin{matrix}0 & 0\\1 & 0\end{matrix}\right]\left[\begin{matrix}a\\1\end{matrix}\right]=\left[\begin{matrix}a\end{matrix}\right]…④\\
\left[\begin{matrix}a & 1\end{matrix}\right]\left[\begin{matrix}0 & 0\\0 & 1\end{matrix}\right]\left[\begin{matrix}a\\1\end{matrix}\right]=\left[\begin{matrix}1\end{matrix}\right]…⑤\\
\left[\begin{matrix}a & 1\end{matrix}\right]\left[\begin{matrix}1 & 0\\0 & 1\end{matrix}\right]\left[\begin{matrix}a\\1\end{matrix}\right]=\left[\begin{matrix}a^{2} + 1\end{matrix}\right]…⑥\\
\left[\begin{matrix}a & 1\end{matrix}\right]\left[\begin{matrix}0 & 1\\1 & 0\end{matrix}\right]\left[\begin{matrix}a\\1\end{matrix}\right]=\left[\begin{matrix}2 a\end{matrix}\right]…⑦
この考え方でいうと⑦のタイプのマスキングに該当する様です?
原関数がx=4(y=8)の時、導関数は$\frac{4×4}{2}=8$

これは物理学の基礎に対応しています。
自由落下運動(Free Fall Movement)とは以下の様な運動を指す。
①重力加速度0.98(=:1,単位m/s^2)の力のかかる向きが進行方向と完全に一致する。
②初速0(m/s)で時間t=0(s)の時の位置y=0(m)とする。
この時、
①時間t=x(s)時点の速度v=gt(m/s)となる。
②時間t=x(s)時点の位置y=1/2×gt^2(m)となる。
③1/2なる数字は(三角形の面積(h(高さ)+v(幅))/2を求める要領で)時間t=0時点の速度v=0(m/s)から時間x(s)時点までの速度v=gt(m/s)までの平均速度(m/s)を求める過程で現れる。
従ってv^2=2gyが成立。
ここで重力係数0.98を1に単純化すると見慣れた微分式$y=x^2→y=2x$の式が現れる訳ですね。そこでは単位m/sが面積に対応します。
- 速度s(m/s)=時間t(s)×重力係数g(m)
- 初速$v_0=0(m/s)$から時間t時点の速度$v_t=gt(m/s)$の平均速度vは$\frac{gt}{2}(m/s)$となる。さらにg=1と置くと$\frac{t}{2}(m/s)$となる。
- x(時間t)時点の位置y(m)は平均速度v(m/s)×時間t(s)=$\frac{gt^2}{2}(m)$となる。 さらにg=1と置くと$\frac{t^2}{2}(m)$となる。
- 従って重力加速度=1と置くと$x^2(t)=2y(m)$となる。
さらにいうと、ここで重力係数$g(0.98) \fallingdotseq 1$と置く事は、それを実数環(Real Ring)すなわち実数列(Real Sequence)を垂直軸(Vertical Axis)z、半径1の単位円を水平軸(Horizontal Axis)xyに取った円筒座標系(Cylindrical Coordinate System)へと射影(Projection)する事を意味します。そうすると嬉しい事にz軸(実数列)の値がそのまま勾配($\frac{z}{1}$)に対応する展開を迎える訳ですね。
三次方程式y=x^3
y=\frac{1}{3}x^3 \\
y'=x^2
導関数の導出過程
f'(x)=\lim_{Δx \to 0}\frac{Δy}{Δx}=\lim_{Δx \to 0}\frac{f(x+Δx)-f(x)}{Δx}\\
=\lim_{Δx \to 0}\frac{(x+Δx)^3-x^3}{Δx}\\
=\lim_{Δx \to 0}\frac{(x^3+3x^2Δx+3xΔx^2+Δx^3)-x^3}{Δx}\\
=\lim_{Δx \to 0}\frac{3x^2Δx+3xΔx^2+Δx^3}{Δx}\\
=\lim_{Δx \to 0}3x^2+3xΔx+Δx^2\\
=3x^2+3*0+0^2=3x^2
これへも上掲の「マスキング」という概念を適用しようとすると、突如として「行列のN乗」なる概念が襲いかかってきます。
- 要するに二次方程式同様、Sympyで以下の様な行列を準備し…
(a+1)^3=a^3+3a^2+3a+1\\
\left[\begin{matrix}\left[ a^{3}, \ a^{2}\right] & \left[ a^{2}, \ a^{2}\right]\\\left[ a, \ a\right] & \left[ a, \ 1\right]\end{matrix}\right]
- 以下の様なマスキング演算"・"によって②が微分結果に一致する事を示したかったのですが、その演算"・"に該当する操作がどうしても見つからないのです(ちなみに4次方程式以降もこの関係は続くが、二項定理と微分の関係について触れた文章をこれまで一度も見た事がなく、誰の関心も集めてこなかった袋小路の匂いがプンプンと…)。
【Python演算処理】パスカルの三角形と二項定理または二項展開
\left[\begin{matrix}\left[ a^{3}, \ a^{2}\right] & \left[ a^{2}, \ a^{2}\right]\\\left[ a, \ a\right] & \left[ a, \ 1\right]\end{matrix}\right]・\left[\begin{matrix}\left[ 1, \ 1\right] & \left[ 1, \ 1\right]\\\left[ 1, \ 1\right] & \left[ 1, \ 1\right]\end{matrix}\right]=a^3+3a^2+3a+1\\
\left[\begin{matrix}\left[ a^{3}, \ a^{2}\right] & \left[ a^{2}, \ a^{2}\right]\\\left[ a, \ a\right] & \left[ a, \ 1\right]\end{matrix}\right]・\left[\begin{matrix}\left[ 1, \ 0\right] & \left[ 0, \ 0\right]\\\left[ 0, \ 0\right] & \left[ 0, \ 0\right]\end{matrix}\right]=a^3…①\\
\left[\begin{matrix}\left[ a^{3}, \ a^{2}\right] & \left[ a^{2}, \ a^{2}\right]\\\left[ a, \ a\right] & \left[ a, \ 1\right]\end{matrix}\right]・\left[\begin{matrix}\left[ 0, \ 1\right] & \left[ 1, \ 1\right]\\\left[ 0, \ 0\right] & \left[ 0, \ 0\right]\end{matrix}\right]=3a^2…②\\
\left[\begin{matrix}\left[ a^{3}, \ a^{2}\right] & \left[ a^{2}, \ a^{2}\right]\\\left[ a, \ a\right] & \left[ a, \ 1\right]\end{matrix}\right]・\left[\begin{matrix}\left[ 0, \ 0\right] & \left[ 0, \ 0\right]\\\left[ 1, \ 1\right] & \left[ 1, \ 0\right]\end{matrix}\right]=3a…③\\
\left[\begin{matrix}\left[ a^{3}, \ a^{2}\right] & \left[ a^{2}, \ a^{2}\right]\\\left[ a, \ a\right] & \left[ a, \ 1\right]\end{matrix}\right]・\left[\begin{matrix}\left[ 0, \ 0\right] & \left[ 0, \ 0\right]\\\left[ 0, \ 0\right] & \left[ 0, \ 1\right]\end{matrix}\right]=1…④
import sympy as sp
a = sp.symbols('a')
a3=a**3
a2=a**2
a1=a
a0000=sp.Matrix([[[a3,a2],[a2,a2]],[[a1,a1],[a1,1]]])
a1111=sp.Matrix([[[1,1],[1,1]],[[1,1],[1,1]]])
a1000=sp.Matrix([[[1,0],[0,0]],[[0,0],[0,0]]])
a0100=sp.Matrix([[[0,1],[1,1]],[[0,0],[0,0]]])
a0010=sp.Matrix([[[0,0],[0,0]],[[1,1],[1,0]]])
a0001=sp.Matrix([[[0,0],[0,0]],[[0,0],[0,1]]])
sp.init_printing()
display(a0000)
print(sp.latex(a0000))
display(a1111)
print(sp.latex(a0000)+"・"+sp.latex(a1111)+"="+"a^3+3a^2+3a+1")
display(a1000)
print(sp.latex(a0000)+"・"+sp.latex(a1000)+"="+"a^3")
display(a0100)
print(sp.latex(a0000)+"・"+sp.latex(a0100)+"="+"3a^2")
display(a0010)
print(sp.latex(a0000)+"・"+sp.latex(a0010)+"="+"3a")
display(a0001)
print(sp.latex(a0000)+"・"+sp.latex(a0001)+"="+"1")
そもそも行列演算では$(a+1)^3$を$(a+1)^2(a+1)$の形で扱う事しか考えてない様にも見えます。
高校数学の行列は旧教育課程の数学Cに含まれていたが,平成21年(2009年)告示の教育課程では数学Cはなくなっており数学Ⅲなどの他の科目にも行列は含まれなかったため,高校では行列計算は原則として習わない.
高校の教育課程からなくなったということは大学入試問題では忠実に反映されるので,行列そのものを出題することはないが,高卒向けや大卒向けの就職試験となるとこの制限はあいまいになる.
この頁では「高校の旧教育課程にあった数学Cのレベル」で「2×2行列に限定して」行列のn乗を扱う.
まさしく高校数学と大学数学の中間領域…
%matplotlib nbagg
import math as m
import cmath as c
import numpy as num
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.animation as animation
# 円柱データ作成
c0=num.linspace(0,m.pi*120,1201,endpoint = True)
s0=[]
for nm in range(len(c0)):
s0.append(complex(m.cos(c0[nm]),m.sin(c0[nm])))
s1=num.array(s0)
z0=num.linspace(-1,1,1201,endpoint = True)
# 「曲率」を計算
cv1=num.linspace(-1,1,1201,endpoint = True)
# cv1=num.sqrt(1-cv0**2)
# 断面線(z)
cutz0=num.linspace(-1,1,61,endpoint = True)
cutz=cutz0[::-1]
cutx=num.abs(cutz)
cuty=num.repeat(0,61)
# 単位円データ作成
u0=num.linspace(0,m.pi*2,61,endpoint = True)
u1=[]
for nm in range(len(u0)):
u1.append(complex(m.cos(u0[nm]),m.sin(u0[nm])))
uc=num.array(u1)
uz0=num.repeat(-1,61)
uz1=num.repeat(-0,61)
uz2=num.repeat(1,61)
# グラフ表示
plt.style.use('default')
fig = plt.figure()
ax = Axes3D(fig)
# 関数定義
def unit_cylinder(n):
plt.cla()
#円柱描画
ax.plot(s1.real*cv1,s1.imag*cv1,z0,color="gray",lw=0.5)
#スポーク描画
#for num in range(len(uc)):
# ax.plot([0,uc[num].real],[0,uc[num].imag],[0,0],color="gray",lw=0.5)
#for num in range(len(uc)):
# ax.plot([0,uc[num].real],[0,uc[num].imag],[1,1],color="gray",lw=0.5)
for num in range(len(uc)):
ax.plot([0,uc[num].real],[0,uc[num].imag],[0,0],color="olivedrab",lw=1)
#単位円描画
ax.plot(uc.real,uc.imag,uz0,color="red",lw=1)
ax.plot(uc.real,uc.imag,uz1,color="green",lw=1)
ax.plot(uc.real,uc.imag,uz2,color="blue",lw=1)
#実数線追加
ax.plot([0,0],[0,0],[-1,1],color="black",lw=1)
ax.plot([0,1],[0,0],[-1,-1],color="red",lw=1)
ax.plot([0,1],[0,0],[0,0],color="black",lw=1)
ax.plot([0,1],[0,0],[1,1],color="blue",lw=1)
ax.plot([1,1],[0,0],[-1,0],color="red",lw=1)
ax.plot([1,1],[0,0],[0,1],color="blue",lw=1)
#断面線描画
ax.plot(cutx,cuty,cutz,color="black",lw=1)
#諸元追加
ax.set_ylim([-1.1,1.1])
ax.set_xlim([-1.1,1.1])
ax.set_zlim([-1.1,1.1])
ax.set_title("Unit Cylinder")
ax.set_xlabel("Real")
ax.set_ylabel("Imaginal")
ax.set_zlabel("Cycle")
# グラフを回転(elev=0にすると水平表示に)
ax.view_init(elev=25, azim=Time_code[n])
Time_code0=num.arange(0,360,6)
Time_code=Time_code0[::-1]
# unit_cylinder(len(s1))
# plt.show()
ani = animation.FuncAnimation(fig, unit_cylinder, interval=50,frames=len(Time_code))
ani.save("output512.gif", writer="pillow")
もしかしたら、この関係は4次方程式経由で四次元の世界へも継承されていく? そんな可能性が示唆されたあたりで以下続報…







