TL;DR
- 全微分
- 行列式
- ヤコビ行列
- 多重積分
- ヤコビアン
これらは高校数学の先にあるもので、多くの数学を応用する分野の書籍や記事で使われることが多いものです。しかし、そういった文書の多くで、これらは読者が知っている前提で、説明無しで用いらていれるように思えます。
この記事は、これらの概念について、順をおって認識、理解していく過程を書いたものです。
そして付録として、同様に説明なして用いられる、極限とイプシロンデルタ論法についての理解の過程も加えてあります。
はじめに
統計や機械学習なども含む応用数学や物理などに含まれる、複数変数関数の積分で、計算しやすくするために座標変換をする話などで、唐突に「ヤコビアン」という概念が用いられます。直交座標の$dxdy$を極座標の$drd\theta$に置き換えるとき、$dxdy \to rdrd\theta$の置き換えが行われ、この$r$はヤコビアンである、といった感じで、あっさりと使われています。
しかし、高校数学を基準に考えると、ヤコビアン自体は範囲外であるし、ヤコビアンまでに至るにはさらに幾つかの段階をへる必要があります。
この記事は、「ヤコビアン」をゴールとして、そこに至るまでの数学の概念を身に着けていこうという趣旨で書いたものです。
全微分について理解する
ヤコビ行列とは、空間から空間への変換関係の全微分を行列で表現です。つまりはヤコビ行列を理解するには、まず全微分がどういうものかの認識を持つ必要があります。
微分の定義と、微小値の存在
高校では一変数関数の微分は学習しています。一変数関数$f(x)$への微分の定義は、
\frac{df(x)}{dx} \equiv \lim_{\Delta \to 0} \frac{f(x + \Delta) - f(x)}{\Delta}
です。($\equiv$は、定義関係で、右辺のパターンの式に対して、左辺の表記法が使える、という関係です。)
高校では微分公式を使うことが多いので忘れさられがちですが、微分において、$f(x)$の各点$x$全体に対して均質な微小値$\Delta$という存在があるということは認識しなくてはいけません。
変数変換のチェーンルール
微分で重要な関係は、変数変換の チェーンルールです。これは変数$x$の関数$f(x)$に対して、変数$s = s(x)$を導入して、$x$を全部$s$で置き換える変数変換をした結果の元の変数$x$が消えた式$f(s)$に変換した場合に、$f(s(x))$を$x$での微分をするときの法則です。
(NOTE: $f(s(x))$とは、$s$が変数$x$の何らかの式で表されていて、もとの$f(s)$の$s$をすべてその$x$の式に代入したもの、つまり変数は$x$の式のことです。微分では、どの変数で表現された式であるか、が重要なので、式を構成する変数を明記する関数にしてあります。)
チェーンルールを丁寧に導出すると以下のようになります。
\begin{align}
\frac{df(s(x))}{dx} &= \lim_{\Delta \to 0} \frac{f(s(x + \Delta)) - f(s(x))}{\Delta} \\
&= \lim_{\Delta \to 0} (\frac{f(s(x + \Delta)) - f(s(x))}{s(x+\Delta) - s(x)} \times\frac{s(x + \Delta) - s(x)}{\Delta}) \\
&= \lim_{\Delta \to 0} \frac{f(s(x + \Delta)) - f(s(x))}{s(x+\Delta) - s(x)} \times \lim_{\Delta \to 0}\frac{s(x + \Delta) - s(x)}{\Delta} \\
&= \lim_{\Delta{s} \to 0} \frac{f(s(x)+\Delta{s}) - f(s(x))}{\Delta{s}} \times \lim_{\Delta \to 0} \frac{s(x + \Delta) - s(x)}{\Delta}
\end{align}
3行目で積の極限を分割したのは、それぞれで極限値が存在する仮定のもと行っています。
最後の行は、微小値$\Delta{s} = s(x+\Delta) - s(x)$を導入して、そこから導かれる$s(x+\Delta) = s(x) + \Delta{s}$を適用しています($\lim_{\Delta \to 0} \Delta{s} = \lim_{\Delta \to 0} (s(x+\Delta) - s(x)) = s(x) - s(x) = 0$なので極限も$\Delta{s} \to 0$にできます)。
この結果に対して、最初の微分の定義に基づいて、微分表現にすることで、
\frac{df(s(x))}{dx} = \frac{df(s)}{ds} \frac{ds(x)}{dx}
という積でつながれるチェーンルールの公式になります。この関係は、$f(u(s(x))) = \frac{df(u)}{du} \frac{du(s)}{ds} \frac{ds(x)}{dx}$のように何段になっても適用できます。
例として、$f(x) = \log(x)^2$を微分するとします。$\frac{df(x)}{dx}$の式を出すには、$s = \log(x)$を導入して$f(s) = s^2$とすれば、$\frac{d}{ds}s^2 = 2s$、$\frac{d}{dx}\log(x) = \frac{1}{x}$なので、チェーンルールより$\frac{df(x)}{dx} = \frac{2s}{x} = \frac{2\log(x)}{x}$が求まります。
偏微分
つづいて、偏微分は、多変数関数において、注目した変数に対してのみ、上記の微小値の極限計算を行うものです。
たとえば二変数関数$f(x,y)$に対して、$x$と$y$それぞれの偏微分は以下の定義になります。
\frac{\partial f(x, y)}{\partial x} \equiv \lim_{\Delta \to 0} \frac{f(x + \Delta, y) - f(x, y)}{\Delta}
\frac{\partial f(x, y)}{\partial y} \equiv \lim_{\Delta \to 0} \frac{f(x, y + \Delta) - f(x, y)}{\Delta}
ふつうは、他の変数を定数扱いして微分の公式を適用することで対応することが多いかもしれません。
全微分
そして本題の全微分です。全微分とは多変数関数に対する単一の微小値にもとづいてする微分のことです。
つまり、多変数関数での多変数それぞれが単一変数の関数であるとみなして扱うことから始まります。
たとえば、二変数関数$f(x,y)$は実は単一変数$t$の関数$f(x(t), y(t))$だったとして扱い、この$t$で微分するのが全微分となります。丁寧にやると
\begin{align}
\frac{df(x, y)}{dt}
&= \lim_{\Delta \to 0} \frac{f(x(t+\Delta),y(t+\Delta)) - f(x(t),y(t))}{\Delta} \\
&= \lim_{\Delta \to 0} \frac{f(x(t+\Delta),y(t+\Delta)) - f(x(t),y(t+\Delta)) + f(x(t), y(t+\Delta)) - f(x(t),y(t))}{\Delta} \\
&= \lim_{\Delta \to 0} \frac{f(x(t+\Delta),y(t+\Delta)) - f(x(t),y(t+\Delta))}{\Delta} + \lim_{\Delta \to 0} \frac{f(x(t), y(t+\Delta)) - f(x(t),y(t))}{\Delta} \\
&= \lim_{\Delta \to 0}\lim_{\Delta{x} \to 0} \frac{f(x(t)+\Delta{x},y(t+\Delta)) - f(x(t),y(t+\Delta))}{\Delta{x}}\times \lim_{\Delta \to 0}\frac{x(t+\Delta)-x(t)}{\Delta} + \lim_{\Delta{y} \to 0} \frac{f(x(t), y(t)+\Delta{y})) - f(x(t),y(t))}{\Delta{y}} \times \lim_{\Delta \to 0}\frac{y(t+\Delta)-y(t)}{\Delta} \\
\end{align}
最後の行はチェーンルールの導出と同様に$\Delta x = x(t+\Delta) - x(t)$、$\Delta y = y(t+\Delta) - y(t)$を使っています。
この極限表現を、偏微分と微分の表現で置き換え、そのあとで$\lim_{\Delta \to 0}\frac{\partial f(x(t), y(t + \Delta))}{\partial{x}} = \frac{\partial f(x(t), y(t))}{\partial x}$を適用したのが、
\frac{df(x(t), y(t))}{dt} = \frac{\partial f(x, y)}{\partial x}\frac{dx(t)}{dt} + \frac{\partial f(x,y)}{\partial y}\frac{dy(t)}{dt}
になり、これが全微分の結果の式になります。3つ以上の変数でも同様に偏微分と共通微小値での微分の積の和になります。
\frac{df(x,y,z)}{dt} = \frac{\partial f(x,y,z)}{\partial x}\frac{dx(t)}{dt} + \frac{\partial f(x,y,z)}{\partial y}\frac{dy(t)}{dt} + \frac{\partial f(x,y,z)}{\partial z}\frac{dz(t)}{dt}
また、両辺の$dt$を取り払って共通変数の$t$の存在を消した
df(x, y) \equiv \frac{\partial f(x, y)}{\partial x} dx + \frac{\partial f(x,y)}{\partial y} dy
を使う場合のほうが多いかもしれません。
しかし、公式として最初にこちらを頭ごなしに入れてしまうと、全微分の意味としての共通変数の存在について知らなかったり、$dy$や$dy$がそもそも何なのかわからなくなり、座標変換にはいってから混乱するようになりがちです。
参考: 中途半端な変数置き換えでの微分
一変数微分での変数変換のチェーンルールでは、もとの変数をすべて消す必要がありました。しかし、一部だけを変数で置き換えた場合、もとの変数も式の中に残ります。こういった場合は、置き換えた変数と元の変数との二変数関数として全微分を行うことで結果として微分が得られます。
つまり、$f(x)$から$s=s(x)$で一部置き換えた二変数関数$f(x, s(x))$を元の変数$x$で全微分することでも微分ができます。
\frac{df(x, s(x))}{dx} = \frac{\partial f(x, s)}{\partial x} \frac{dx}{dx} + \frac{\partial f(x,s)}{\partial s}\frac{ds(x)}{dx}
もちろん$x$を$x$で微分するので$\frac{dx}{dx} = \frac{d}{dx}x = 1$を適用します。
例として、$f(x) = x \mathrm{e}^{x}$へ$s = \mathrm{e}^x$を適用した$f(x, s) = x s$について、$x$で全微分すると、
\frac{df(x, s)}{dx} = s \times 1 + x \times \frac{ds(x)}{dx} = \mathrm{e}^x + x\mathrm{e}^x = (1+x) \mathrm{e}^x
となり、たとえば積の公式などで導出したものとも同じ結果になります。
空間の変換としての正方行列と行列式
ヤコビ行列はその名の通り「行列」で表現されるものなので、行列についての基礎知識が必要です。
ここでは正方行列に限定し、行列の「積」による作用の意味について確認するものです。
正方行列の積の意味
行列を用いる応用先は多岐にわたります。正方行列は積をとることで、空間上の点を一様に移す変換器として用いられます。
つまり、点と行列の積を取った結果は、変換先の点となります。
二次元空間では、
\begin{pmatrix}
x_d\\y_d
\end{pmatrix}
=
\begin{pmatrix}
a & b\\c & d
\end{pmatrix}
\begin{pmatrix}
x_s\\y_s
\end{pmatrix}
で、$x_d = ax_s + by_s$, $y_d = cx_s + d y_s$が変換先の点になります。
線や面といった点の集合も、一様に点の集合へと変換されます。
行列が定数で構成される場合、変換先はxとyの1次の項しか無いので、直線は曲がったりせず、(しかも隣接関係を維持したまま)直線に移ることになります。
行列式の意味
空間上の基底(座標軸上の単位ベクトル)で張られる単位領域を行列で変換するとどうなるかを考えます。
2次元空間の場合、基底$(1, 0), (0, 1)$から、頂点$O=(0,0), X=(1, 0), Y=(0, 1), P=(1,1)$の面積1の正方形を張ります。
この各頂点を行列
A \equiv
\begin{pmatrix}
a & b \\ c & d
\end{pmatrix}
で変換すると、頂点が$O=(0, 0), X_d=(a, c), Y_d=(b, d), P_d=(a+b, c+d)$に移った平行四辺形になります
($X_d = P_d - Yd$かつ$Y_d = P_d - X_d$で直線$OX_d$と直線$P_dY_d$および直線$OY_d$と直線$P_dX_d$それぞれ並行)。
この平行四辺形の面積$OX_dY_dP_d$は$X_d$と$Y_d$のクロス積の$ad-bc$になります。
行列での変換では、一様に行われるので面積$S$の領域を変換すると、変換後の面積は$(ad-bc)S$になります。
ある行列の「行列式(determinant)」というのは、その行列による変換後の領域の拡大率を意味します。
行列式は、$\det(A)$とか$|A|$とかで表現されます。二次行列の場合、
\det(A) = |A| =
\begin{vmatrix}
a & b \\ c & d
\end{vmatrix}
\equiv ad - bc
となります。
図1: 左図の3点(0,1)、(1,0)、(1,1)を、行列式が6の行列Aで変換した結果が右図。左図では面積1の正方形が、変換後の右図では面積6の平行四辺形になる。
変換先で領域内の関係が鏡像反転したときには、行列式は負の値になります。
また、変換によって領域が消えたとき、つまり面が線や点になってしまうなど次元が減るとき、行列式は0になります。
行列式というのは、行列での変換のうち、拡大の側面だけに着目するもの、ともいえます。
参考: 正方行列の固有分解と固有値と固有ベクトルの意味
正方行列は空間を同一の空間に移す性質がありますが、この性質から、一つの行列を、その拡大要素の行列とその基底移動要素の行列とに分解するのが「固有分解」です。
固有分解とは、行列Aを、その「固有値(eigenvalue)」を並べた対角行列Dと、Dの固有値順に「固有ベクトル(eigenvector)」を並べた行列Vとで構成する行為です。
A = VDV^{-1}
行列による領域変換で空間全体を変換すると、原点からの角度が変わらずに原点からの距離だけ変化する原点を通る直線が、空間の次元と同じ数存在しています。その直線(の傾きを表す単位ベクトル)が「固有ベクトル」です。
すなわち固有ベクトルが乗る原点を通る直線上の点は回転せず、ただ拡大縮小だけされます。この拡大率が「固有値」です。「固有値」も「固有ベクトル」も無説明で用いられやすい用語なので、このような空間変換においての意味を覚えておくと良いです。
固有分解というのは、1つの行列が行う変換を
- 変換で向きが変わらない固有ベクトルを直交基底へ移す変換($V^{-1}$)を行い
- つづいて基底の拡大縮小($D$)を行い
- 最後に直交基底をそれぞれの固有ベクトルに移す(回転せん断)変換($V$)をする
という3つの(単純な)変換の連鎖で表したものです。
基底から固有ベクトルへの変換をする$V$及び$V^{-1}$の行列式は、互いに逆数になっているため($\det(V^{-1}) = \frac{1}{\det(V)}$)、基底の拡大縮小が領域の大きさを変える本質になります。そのため、元の行列の行列式の値は、固有値の対角行列$D$の行列式の値と同じになります。
そしてこれは、それぞれの基底での拡大、つまり、行列の固有値$\lambda_i$を、すべてかけ合わせた値と同じになります。
\det(A) = \det(VDV^{-1}) = \det(D) = \prod \lambda_i
図2: 左上 - 基底ベクトルとその正方形領域(青)、および、行列Aの固有ベクトルとその平行四辺形領域(赤)。それぞれのベクトルの長さは1。
右上 - 基底ベクトル及び固有ベクトルに、固有ベクトルの逆行列をかけた結果(赤の固有ベクトルが基底に移る)。
左下 - 右上にさらに固有値の対角行列をかけ合わせた結果(固有ベクトルが、対応する固有値ぶん掛け合わされた長さになる。)。
右下 - 左下にさらに固有ベクトルの行列をかけ合わせた結果(基底ベクトルの変換後の平行四辺形の面積は、左下での固有ベクトル領域の変換後の矩形の面積と同じ、固有値の積となる)。
空間変換としての座標変換とヤコビ行列
ここで、全微分と行列から、ヤコビ行列を導出し、それがどういった意味なのかを確認していきます。
空間変換として座標変換を認識する
たとえば直交座標から極座標への座標変換は、ふつうの認識では同一空間での点の違う表現方式といして扱い、$(x, y) = (r \cos(\theta), r \sin(\theta))$のように表現します。
しかし、微分や積分のことを考える場合、同一点の表現の置き換えとしての認識をするのはやめて、ある二次元空間の点$(r, \theta)$ から、全く別の二次元空間の点$(x, y)$への変換である、と認識したほうが理解しやすいです。
つまり2つの空間があって、単にその間の点どうしの対応関係が
\begin{pmatrix}
x \\ y
\end{pmatrix}
=
\begin{pmatrix}
r \cos(\theta) \\ r \sin(\theta)
\end{pmatrix}
である、二次元空間から別の二次元空間への対応関係に過ぎないのだと認識することです。$(x,y)$空間での$x$と$y$と同じように、元の空間の上では$r$と$\theta$の間に半径だ角度だといった特別な意味や関係はありません。
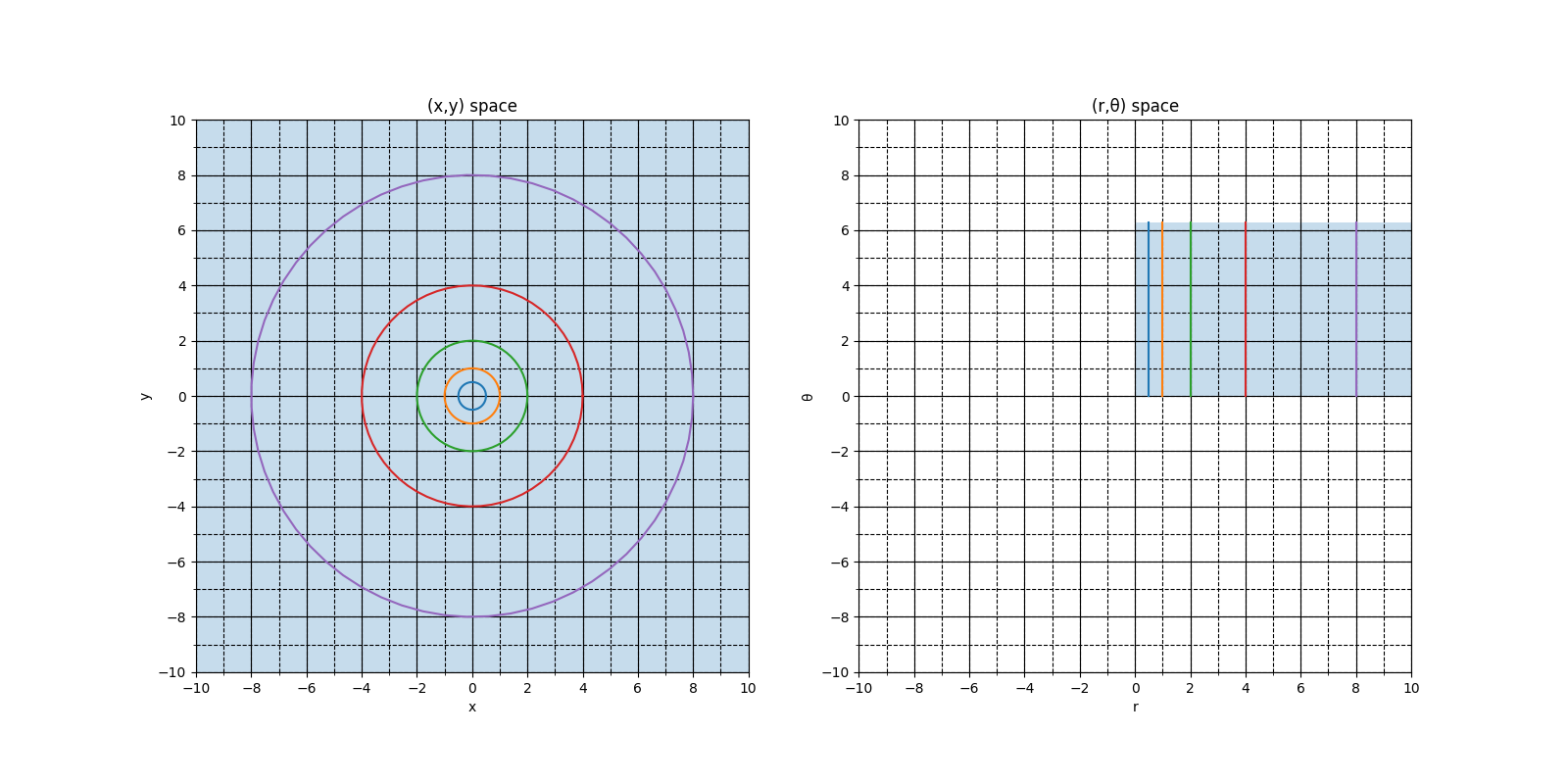
図形でいうと、元の空間は$r$軸と$\theta$軸が直交していて、そのうち$r \geqq 0$かつ$0 \leqq \theta < 2\pi$の領域の点から、$x$軸と$y$軸で張る空間全域の点へ対応付けたものです。
より具体的な極座標から直交座標への変換イメージは、$\theta$軸と並行な$(r, 0)$から$(r, 2\pi)$までの線分が、$xy$空間上の半径$r$の円周の線へと曲げるものです。
図3: 左図 - XY空間全域と原点を中心にした同心円。 右図 - rθ 空間におけるXY空間の領域とXYでの各同心円に対応する直線。
空間変換の全微分とヤコビ行列
二次元の極座標空間から二次元の直交座標空間の対応関係
\begin{pmatrix}
x \\ y
\end{pmatrix}
=
\begin{pmatrix}
r \cos(\theta) \\ r \sin(\theta)
\end{pmatrix}
を全微分します。各要素ごとに全微分します。
\begin{pmatrix}
\frac{dx}{dt} \\
\frac{dy}{dt}
\end{pmatrix}
=
\begin{pmatrix}
\cos(\theta) \frac{dr}{dt} - r \sin(\theta) \frac{d\theta}{dt}\\
\sin(\theta) \frac{dr}{dt} + r \cos(\theta) \frac{d\theta}{dt}\\
\end{pmatrix}
これを点$(r,\theta)$の周りの微小領域$(\frac{dr}{dt}, \frac{d\theta}{dt})$から、点$(x,y)$の周りの微小領域$(\frac{dx}{dt}, \frac{dy}{dt})$への変換とみなし、変換行列との積で表現します。
\begin{pmatrix}
\frac{dx}{dt} \\
\frac{dy}{dt}
\end{pmatrix}
=
\begin{pmatrix}
\cos(\theta) & - r \sin(\theta)\\
\sin(\theta) & r \cos(\theta)\\
\end{pmatrix}
\begin{pmatrix}
\frac{dr}{dt} \\
\frac{d\theta}{dt}
\end{pmatrix}
ある空間変換での関係においての、この微小領域から微小領域への変換行列のことを「ヤコビ行列」と呼びます。
このような具体例ではなく、任意の2空間$(u,v)$と$(x,y)$の間の変換関係において一般化すると、ヤコビ行列は偏微分を要素とする行列になります。
\begin{align}
\begin{pmatrix}
\frac{dx}{dt} \\
\frac{dy}{dt}
\end{pmatrix}
&=
\begin{pmatrix}
\frac{\partial x(u,v)}{\partial u}\frac{du}{dt} + \frac{\partial x(u,v)}{\partial v} \frac{dv}{dt}\\
\frac{\partial y(u,v)}{\partial u}\frac{du}{dt} + \frac{\partial y(u,v)}{\partial v} \frac{dv}{dt}\\
\end{pmatrix}\\
&=
\begin{pmatrix}
\frac{\partial x(u,v)}{\partial u} & \frac{\partial x(u,v)}{\partial v}\\
\frac{\partial y(u,v)}{\partial u} & \frac{\partial y(u,v)}{\partial v}\\
\end{pmatrix}
\begin{pmatrix}
\frac{du}{dt} \\
\frac{dv}{dt}
\end{pmatrix}
\end{align}
すなわちヤコビ行列$J_{(u,v)}$は、
J_{(u,v)} \equiv
\begin{pmatrix}
\frac{\partial x(u,v)}{\partial u} & \frac{\partial x(u,v)}{\partial v}\\
\frac{\partial y(u,v)}{\partial u} & \frac{\partial y(u,v)}{\partial v}\\
\end{pmatrix}
となります。3次以上の空間へに対しても同様の偏微分要素の行列になります。
注意点としては、ヤコビ行列は各点ごとの行列である、ということです。
すなわち、パラメータとして点が必要な関数の行列であることです。
これは普通の一変数関数の微分値が各点によって変わることと同じ意味になっています。
ヤコビ行列は多次元空間への(全)微分を表すもの、ともいえます。
その点での傾きとしてみると微分$\frac{dy}{dx}$は、x軸での微小値$\Delta$ぶん増えたら$\frac{dy}{dx}\Delta$増えるものになります。すなわち微分は、x軸上での微小値を、y軸での微小値へスケールを変換させる変換器とみなせます。同様に、ヤコビ行列は、空間の微小領域から変換先空間の微小領域への変換器であるとみなせます。
領域への多重積分と微小領域変換の拡大率としてのヤコビ行列式
最後に、多重積分とヤコビアンの関係について確認します。
多重積分
多変数関数にたいして、多変数でなす多次元空間上の領域に対して積分することを「多重積分(重積分)」といいます。(他には多次元空間の曲線上で積分する線積分などがある)。
\iint_{D}f(x,y)dxdy
この$D$は積分対象の$(x,y)$の領域のことで、実際には領域を表す条件式だったりします。領域とは簡単に言うと、二次元空間なら面のような、繋がっている点の集まりのことで、空間での量が測れる存在です。$D$部分には、点集合表現そのものや、点集合の内包表現での条件式が直接埋め込まれることも普通です。
とくに領域の形が、空間上で矩形(長方形)領域になっている場合は、一変数積分の多重化させた表現ができます。
\int_{a_x}^{b_x} \int_{a_y}^{b_y} f(x,y)dxdy
矩形領域での積分の場合には、変数ごとに分離して積分するなどで、計算がしやすくなります。
多重積分の座標変換とヤコビ行列式
まず具体的な多重積分での座標変換の例として、円領域$\sqrt{x^2+y^2} \leqq a$での多重積分を考えます。これを直交座標$(x,y)$で直接積分するのではなく、極座標$(r,\theta)$に変換して積分することを考えます。
V_{(x,y)} = \iint_{\sqrt{x^2+y^2} \leqq a} f(x, y) dydx
極座標への変換は、点$(x, y)$を $(r \cos(\theta), r \sin(\theta))$で置き換えることです。しかし、変換後の$(r, \theta)$空間においては矩形領域として積分したいとします。つまりこの積分領域を、$0 \leqq r \leqq a, 0 \leqq \theta \leqq 2\pi$の矩形として積分する、ということです。つまり、以下のスタイルの矩形領域での多重積分に変換するのが目標になります。
\int_{0}^{2\pi} \int_{0}^{a} g(r, \theta) drd\theta
しかし、多重積分で求めたいのは$(r,\theta)$空間での値はなく、$(x,y)$空間での積分値を得たいわけです。すなわち積分計算で使う微小領域$drd\theta$は$(x,y)$空間での量で全領域ぶんを積み重ねていく必要があります。
つまり、変数変換での多重積分のためにはまず、微小領域$drd\theta$の$(x,y)$空間での量を求める必要があります。
V_{(x,y)} = \int_{0}^{2\pi} \int_{0}^{a} f(x(r,\theta),y(r,\theta)) (? \times drd\theta)
ここで出てくるのがヤコビ行です。ヤコビ行列$J_{(r,\theta)}$は、微小領域の$(dr, d\theta)$空間を、微小領域の$(dx,dy)$空間へ変換する行列とみなせます。
\begin{pmatrix}
dx \\
dy
\end{pmatrix}
=
\begin{pmatrix}
\cos(\theta) & - r \sin(\theta)\\
\sin(\theta) & r \cos(\theta)\\
\end{pmatrix}
\begin{pmatrix}
dr \\
d\theta
\end{pmatrix}
多重積分で必要なのは$drd\theta$へ掛ける、微小領域の量の**変換後の大きさ(拡大比率)**です。行列式こそが変換行列の拡大率であるので、すなわち、ヤコビ行列の行列式$\det(J_{(r,\theta)})$が、この微小領域の拡大率ということになります。
\begin{align}
\det(J_{(r,\theta)}) &= \det
\begin{pmatrix}
\cos(\theta) & - r \sin(\theta)\\
\sin(\theta) & r \cos(\theta)\\
\end{pmatrix} \\
& = \cos(\theta) \times r \cos(\theta) - -r \sin(\theta) \times \sin(\theta)\\
&= r (\cos^2(\theta) + \sin^2(\theta)) \\
&= r
\end{align}
よって多重積分の極座標変換は、
V_{(x,y)} = \int_{0}^{2\pi} \int_{0}^{a} f(x(r,\theta),y(r,\theta)) (r \times drd\theta)
となります。このうち微小領域への拡大率である、ヤコビ行列の行列式が、「ヤコビ行列式」もしくは「ヤコビアン」と呼ばれるものです。
これを任意の二次元空間のあいだでの変数変換の表現にすると
\begin{align}
V_{(x,y)} = \iint_{D_{(x,y)}} f(x,y) dxdy
&= \iint_{D_{(u,v)}} f(x(u,v),y(u,v)) \det(J_{(u,v)}) dudv \\
& \left( = \iint_{D_{(u,v)}} f(x(u,v),y(u,v)) (\frac{\partial x(u,v)}{\partial u} \frac{\partial y(u,v)}{\partial v} - \frac{\partial x(u,v)}{\partial v} \frac{\partial y(u,v)}{\partial u}) dudv \right)\\
\end{align}
となります。
簡単な例として半径$a$と高さ$b$の円錐の体積を求めてみましょう。
図4: 2変数関数f(x,y)による円錐の図
積分する円錐の式は底点$(x, y)$での位置の高さを表す$f(x,y) = b(1 - \frac{\sqrt{x^2+y^2}}{a})$で、これを円領域$\sqrt{x^2+y^2} \leqq a$で積分することで求めます。つまり、
V_{(x,y)} = \iint_{\sqrt{x^2+y^2} \leqq a} b\left(1-\frac{\sqrt{x^2+y^2}}{a}\right) dydx
この多重積分を、極座標$(x,y) = (r\cos(\theta),r\sin(\theta))$より、$\sqrt{x^2+y^2} = r$となることを用いて多重積分の座標変換をして、矩形領域への多重積分として解いていく過程は以下のようになります。
\begin{align}
V_{(x,y)} &= \int_{0}^{2\pi} \int_{0}^{a} b(1 - \frac{r}{a}) r drd\theta \\
&= \int_{0}^{2\pi} b\left( \int_{0}^{a}(r - \frac{r^2}{a})dr \right) d\theta \\
&= \int_{0}^{2\pi} b\left[ \frac{r^2}{2} - \frac{r^3}{3a} \right]_{0}^{a} d\theta \\
&= \int_{0}^{2\pi} b\left( \frac{a^2}{2} - \frac{a^2}{3} - 0 + 0\right) d\theta \\
&= \int_{0}^{2\pi} \frac{ba^2}{6} d\theta \\
&= \left[\frac{ba^2}{6}\theta \right]_{0}^{2\pi} \\
&= \frac{ba^2}{6} \times 2\pi - 0 \\
&= \frac{ba^2\pi}{3}
\end{align}
円錐の体積は、円柱の体積($a^2\pi \times b$)の三分の一であることから、正しく算出できていることがわかります。
付録: 極限の積の分割とイプシロンデルタ
微分のチェーンルールの導出において、極限の積分割を導入しました。
これは「$\lim_{x \to c}f(x) = a$かつ$\lim_{x \to c}g(x) = b$ならば、$\lim_{x \to c}f(x)g(x) = ab$が成立する」という定理を使用したものです。この極限値の$a$と$b$を極限表現に戻したものが、極限の分割
\lim_{x \to c}f(x)g(x) = \lim_{x \to c}f(x) \lim_{x \to c}g(x)
です。
ここで重要なことは、分割する$f(x)$と$g(x)$双方に極限値が存在することが、前提となっている点です。
たとえば、$\Delta \times \frac{1}{\Delta}$では、後者が収束せず極限値が存在できないので分割の条件が成立しません。
極限とイプシロンデルタ論法
極限の式$\lim_{x \to c}f(x) = a$ですが、これは値$a$に対してイプシロンデルタ論法という論理式が成立するなら、その値と同値扱いする、という意味を表しています。
そして、イプシロンデルタ論法というのは以下の論理式です。
\forall{\epsilon}\exists{\delta}.|x-c|<\delta \rightarrow |f(x) - a| < \epsilon
この論理式が言いたいことは、「$a$そのものではないどんな値$(a\pm\epsilon)$に対しても、より$a$に近い$f(c\pm\delta)$を出す$\delta$を提供できる」という意味です。
これは「$x$を$c$に近づけていけば、$f(x)$は($a$そのものではないかもしれないけど)、$a$ではない他のどんな具体的な値と比べても、より$a$に近づいていくものにはなっている」という認識もできます。
$\lim$をつけた極限とは、イプシロンデルタ論法的に際限なく近づいていく値は、その値そのものと同値とみなして扱うという操作であるともいえます。
有名な$0.999.... = 1$ですが、これは$\lim_{x \to 0} (1 - \frac{1}{10^{\frac{1}{x}}}) = 1$を意味するものだといえるでしょう。$f(x) = 1 - \frac{1}{10^{\frac{1}{x}}}$は、$f(\frac{1}{2}) = 0.99$、$f(\frac{1}{3}) = 0.999$と、$x$が0に近づくほど、$f(x)$は1に近づいていきます。($x$自体は0になれないし、$f(x)$自体も1にはならない点は注目すべきところです)
さてこの論理では、任意の$\epsilon$に対応した$\delta$が存在する必要があります。
すなわち**$\epsilon$をパラメータとした$\delta(\epsilon)$が定まる**必要があります。
この例では、$\epsilon = 1 - f(x) = 10^{-n}$のときは$x = \frac{1}{n}$になるので、それより小さい値を$\delta$にすればよいのです。逆にこの$n$を$\epsilon$で表現すると、$n = -\log_{10}(\epsilon)$であるので、$x = \frac{-1}{log_{10}(\epsilon)}$となるので、
\delta(\epsilon) < \frac{-1}{log_{10}(\epsilon)}
の条件を満たす$\delta(\epsilon)$を与えれば良いことになります。(たとえば、$\delta(\epsilon) = \frac{-1}{log_{10}(\epsilon)-1}$など)
極限の積の分割を導出する
極限の分割は、「$\lim_{x \to c}f(x) = a$かつ$\lim_{x \to c}g(x) = b$ならば、$\lim_{x \to c}f(x)g(x) = ab$が成立する」です。すなわち
- $\forall{\epsilon_{a}}\exists{\delta_{a}}.|x-c|<\delta_{a}\rightarrow |f(x)-a|<\epsilon_{a}$
- $\forall{\epsilon_{b}}\exists{\delta_{b}}.|x-c|<\delta_{b}\rightarrow |g(x)-b|<\epsilon_{b}$
を前提として
- $\forall{\epsilon}\exists{\delta}.|x-c|<\delta\rightarrow |f(x)g(x)-ab|<\epsilon$
を導出できれば良いことになります。
ここで、まず注意したいのは、論法の対象が$1-\frac{1}{10^{\frac{1}{x}}}$のような具体的な式ではなく、関数表現のままである点です。具体的な式の場合は$\epsilon$に対応する$\delta$のほうも具体的な式として表現できますが、関数の場合にはふつうそうは行きません。
もし$f(x)$が単射であれば、逆関数で$\delta = f^{-1}(a+\epsilon_0)-c$というような形で記述できます。しかし単射が前提でない場合には、「$f(c+\delta)=a+\epsilon_0$になるような$\delta$の一つ」といった表現をすることになります。これがより短い、「この$\epsilon_0$に対応した$\delta$(が存在するので論理式が成立する)」のような表現が使われる意味です。
この時点で、具体的に導出する対象は$\delta$から、そのパラメータである$\epsilon_0 < \epsilon$な$\epsilon_0$へと移ります。この**$\epsilon_0$を、$\epsilon$を始めとする式中や前提に含む変数を用いた具体表現を作る**ことになります。
一方、前提のほうからは$\delta_{a}(\epsilon_{a})$と$\delta_{b}(\epsilon_{b})$とが存在済みで使用できることを意味します。しかし、こちらも対象が関数表現のままなので、$\epsilon_{a}$と$\epsilon_{b}$のほうへ具体的な値を割り当てることがメインになります。
この論理式の導出では、$|f(x)g(x)-ab|$を変形していき、$\epsilon_{a}$と$\epsilon_{b}$とを用いて表現できる$\epsilon_0 < \epsilon$を見つけます。
\begin{align}
|f(x)g(x)-ab| &= |f(x)g(x) - f(x)b + f(x)b - ab| \\
&= |f(x)(g(x) - b) + (f(x) - a)b|\\
&= |f(x)(g(x) - b) - a(g(x) - b) + a(g(x) - b) + (f(x) - a)b|\\
&= |(f(x) - a)(g(x) - b) + a(g(x) - b) + (f(x) - a)b|\\
&< |f(x) - a||g(x) - b| + |a||g(x) - b| + |f(x) - a||b|\\
&< \epsilon_{a}\epsilon_{b} + |a| \epsilon_{b} + |b|\epsilon_{a} \\
\end{align}
(前提にある$|f(x) - a| <\epsilon_{a}$と$|g(x) - b| <\epsilon_{b}$を適用しました。)
つまり、
|f(x)g(x) - ab| < \epsilon_{a}\epsilon_{b} + |a| \epsilon_{b} + |b|\epsilon_{a} < \epsilon
の関係があります。
$\delta$の存在証明としては、$\epsilon_{a}$と$\epsilon_{b}$はどちらも任意の値が取れることから、「$\epsilon_0 = \epsilon_{a}\epsilon_{b} + |a| \epsilon_{b} + |b|\epsilon_{a} < \epsilon$を満たす$\epsilon_{a}$と$\epsilon_{b}$による$\epsilon_0$に対応する$\delta$」が存在するのでこの関係は成立するものである、で終われます。
(以降は、存在性だけでなく、具体例まで求める話です。)
より具体的な$\epsilon_{a}$と$\epsilon_{b}$の導出をするには、3分割した$\frac{\epsilon}{3}$で抑えるような、それぞれの項を考えます。
$|b|\epsilon_{a} < \frac{\epsilon}{3}$を満たすとすれば、$\epsilon_{a} < \frac{\epsilon}{3|b|}$になります。$|b|$が0になる場合も考えて、$\epsilon_{a} < \frac{\epsilon}{3\max(1, |b|)}$にして$\frac{\epsilon}{3}$より大きな値にならないようにします。同様に$\epsilon_{b} < \frac{\epsilon}{3\max(1, |a|)}$が得られます。
しかし、$\epsilon_{a}\epsilon_{b} < \frac{\epsilon}{3}$にもしたいので、($\epsilon>1$なら2つ掛けると大きくなりうるため)$\frac{\epsilon}{3}$ではなく、$\frac{\min(\epsilon, 1)}{3}$で掛けて大きくならないように抑えることにすれば、$\epsilon_{a}\epsilon_{b} \leqq \frac{\epsilon}{9}$で抑えられることが保証されます。
つまり、具体的な$\epsilon_{a}$と$\epsilon_{b}$は、
\begin{align}
\epsilon_{a} &< \frac{\min(\epsilon,1)}{3\max(1, |b|)}\\
\epsilon_{b} &< \frac{\min(\epsilon,1)}{3\max(1, |a|)}
\end{align}
を満たすような適当な値を選べばよいことになります。たとえば、3の代わりに4で割った値がそれに当てはまる例のひとつです。この$\epsilon_{a}$と$\epsilon_{b}$を適用した$\epsilon_0$は以下のとおりです。
\epsilon_0 = \frac{\min(\epsilon,1)^2}{16\max(1,|a|)\max(1,|b|)} + \frac{|a|\min(\epsilon,1)}{4\max(1,|a|)} + \frac{|b|\min(\epsilon,1)}{4\max(1,|b|)} < \epsilon
どんな$\epsilon$が来ようとそれより小さいこの$\epsilon_0$に対応する$\delta$が存在することから、積の分割の関係は成立できるのです。
リンク
- 埋め込み画像の生成コード(python3 & matplotlib): https://gist.github.com/bellbind/bcafacb3b2843e6e0cce46319b021577