計算数学(Computational Mathematics)の何よりの面白さは、思わぬ方向に概念の精緻化を要求される所にあったりします。進化の過程で育まれてきた「(生物が進化の過程で獲得してきた様な、純粋な形では数理に全面依存してはいない)粗雑な代数構造体系」を「コンピューター(すなわちそれを駆動させている、純粋に数理の積み上げにのみ立脚する精緻な代数構造体系)はそのままの形では解ってくれない」のですね。
【無限遠点を巡る数理】「ピタゴラスの定理」と「デカルト座標系」の狭間
ならばどう考えれば良いのでしょう?
- 前者をとりあえず仏法哲学でいう「相依性(相互依存性)縁起論の世界」すなわち「観測者が識知可能な、すなわち一応は原因と条件の結果の関係で語り得る様な(ただしその生滅の連鎖を相応の精度を有する観測結果とそれから抽出された数理のみで説明し切れる段階までは至ってない)無明の諸概念集合(Concepts Set)」と置く。
縁起 - Wikipedia - 西洋哲学の世界から出発したいなら、例えば「真理の全体構造(Overall Structure of Truth)」を三段論法(Syllogism)に従って「すべてのPはQである」「あるPはQである」「すべてのPはQではない」「あるPはQではない」とか、背理法(Proof by Contradiction)に従って「AならばBである(命題)」「BならばAである(逆)」「AでないならBでない(裏)」「BでないならAでない(対偶)」といった四象集合(Set of Opposition Square)に分類しようとする古典論理概念(Concept of Classical Logic)辺りにでも軸足を置けば良い。この場合「縁起(無明)の世界」は「Qではない」と切り捨てられる範囲に該当する。
古典論理 - Wikipedia
いずれにせよ最初に辿り着く結論は同じ。それぞれが莫大な時間と手間を掛けて蓄積されてきた英知とはいえ「人間の脳なる古参のハードウェア上ではそれそれがそれなりに適切に見える形で動いても、コンピューターなる新参者のハードウェア上ではウンともスンともいわない」という一点において「みんな違ってみんなダメ」なのです。
山本一郎氏が絶賛する『みんなちがって、みんなダメ』とは
別に現在のComputer Architectureの在り方が人間の英知を凌駕したといった壮大なパラダイムシフトが起こった訳でもありません。「現在のComputer Architectureもそれなりにバカ(なので、そのバカにでも分かるアルゴリズムしか受け付けない)」なる情けない現実が実存するだけです。それで悔しくて「現在はただの過渡期。近い将来(量子コンピューティングみたいな超技術を統合した)真の意味で人間の脳に対応するハードウェアが現れる」と予言し続ける人もいれば、諦めて「その夢は1980年代にピークを迎えた第二次人工知能ブームまでにほぼ潰え、1990年代に端を発する第三次人工知能ブームからは(現在のComputer Architectureの在り方にアルゴリズム開発者としての人間側が適応した)新たな試みが始まっている」と考える様になった人もいます。そして後者の立場に立つなら上掲の「コンピューター(すなわちそれを駆動させている、純粋に数理の積み上げにのみ立脚する精緻な代数構造体系)の世界」はこう図式化される訳です。
- プラトンが「ドクサ(Doxa)」すなわち「(最も純粋な定義においては)分析なき経験結果の寄せ集めから勝手に自明の場合(Trival Case)として生じる、すなわち特定の背景理論を抽出して法則化して適用範囲を決定する様な知的作業抜きで積み重ねられるバイアス(Bias=偏誤)の単なる寄せ集め」に対峙させる形で提言し、ミシェル・フーコー「言葉と物(Les mots et les choses,1966年)」「知の考古学(L'Archéologie du savoir, 1969年)」においてその定義がさらに「各時代における知識の体系を成立させてきた認識構造の原則的在り方」へと拡張された「エピステーメー(Episteme)」概念から出発する。ちなみにトーマス・クーン「科学革命の構造(The Structure of Scientific Revolutions,1962年)」の提言に従ってこの概念の適用範囲を科学的実証主義(Scientific Positivism)の歴史上におけるイノベーションの不連続性に絞ったのが「パラダイム・シフト(Paradigm Shift)」概念となる。この立場からは上掲の対立構造が「現在のComputer Architectureの在り方は新たなEpistemeを提供したか?(いや、如何なる形でもそれ自体は新たなEpistemeを提供してはいない!!)」「何かParadigm Shiftを引き起こしたか?(いや、如何なる形でもそれ自体は新たなParadigm Shiftを引き起こしてなどいない!!)」問題と俯瞰される。
バイアスのご先祖様??【哲学図解】『ドクサとエピスメーテー』
【エピステーメーとは】その意味からフーコーの議論をわかりやすく解説 - 実際「新たなEpistemeの提供者」や「新たなParadigm Shiftの原動力」の立場を主張しているのはコンピューター自身ではなく(まぁコンピューター自身は現段階においてはまだまだ自らの主張を展開し得る発達段階にない)自然数集合(Set of Natural){1,2,3,…,Inf(inity)}や、加法単位元(Additive Identity)0と乗法単位元(Multiplicative Identity)1を共に備える整数環(Ring of Integers){-Inf,…,-3,-2,-1,-,1,2,3,…,Inf}といった基本概念からの再出発を果たし「特定の演算結果の集合とその積」として自らの全体構造を記述する様になった現代数学(Modern Mathematics)の世界なのである。実際オイラーの公式(Eulerian Formula)exp(πi)=Cos(θ)+Sinθiやガウスの巡回群(Gaussian Cyclic Group)i^x=1の概念抜きにはコンピューターは円すら描けない訳で、この指摘には確かに相応のアドバンテージが存在する。
【初心者向け】群論概念の根幹
1の冪根 -Wikipedia
とはいえコンピューターは本当にバカなので「現代数学そのもの」が走ってる訳でもありません。何しろコンピューターは、というよりそのメモリ構造たる配列概念には、その実装段階における制約上整数環(Ring of Integers){-Inf,…,-3,-2,-1,-,1,2,3,…,Inf}の概念すらまともに再現する機能が実装されているとはいえない有様なのです。
統計言語Rにおける実装例
# コンピューター上における自然数表現
> seq(1,5,length=5)
[1] 1 2 3 4 5
# コンピューター上における整数表現
> seq(-5,5,length=11)
[1] -5 -4 -3 -2 -1 0 1 2 3 4 5
- まぁ実際のプログラム上「運用でカバー」なる現状に誰も不満を抱えてないというだけの話に過ぎないのだが(実現コストを考えると「無駄」に分類される事象という事)。そもそも加算(Countable)で直積可能(Productable)な数が主な対象で無限遠(Inf(inity))の概念を扱うのが苦手。
【無限遠点を巡る数理】無限直線/無限円/無限球面そして無限トーラス?
一方、この世界観においてはとりあえず全体から抽出した次元や数値といった諸概念の独立性が担保され、アルゴリズム遂行によって欲しい答えがえられる「(相応の精度を有する観測結果とそれから抽出された数理のみに立脚する)三昧の世界」と、この条件が未達成の「(計測値がコイントスの様に計測の都度1か0か変わったり、何時の間にかπ/2ラジアン(90度)が-π/2ラジアン(-90度)に挿し変わっている様な不安的極まりない)無明の世界」の境界線は以下の形で与えられるのです(西洋哲学でいうと「何かがそうであるかないかの境界線」辺りに比定される?)。
三昧(サンマイ)とは何? Weblio辞書
- とりあえず半径rの球面を想定し、任意の対蹠(Antipodes=北極と南極に該当する距離関係の2点)間を結ぶ共役複素数(Conjugate Complex Number)の遷移を抽出する。円を60分割するとそれぞれの観測方向に「15本の波紋」が現れる。「波紋の進行方向」を特に定めなければ(実際それを定める事に計算上特別な意味がない)観察者が主観で補うに任されるが、この現象自体も上掲の「無明」状態の一種とはいえよう。
【初心者向け】複素共役のアニメーション表示について。
- そもそも「進行方向」自体は関数グラフ上にも表示されてない(実際定める事に計算上特別な意味がない)。数学の世界においては(計算に差し支えない範囲においては)「三昧の世界」と「無明の世界」がこうやって思わぬ形で隣接しており、その視覚化は、かかる現実を容赦無く暴き立てる(コンピューターはこの作業を容易にはするものの、手計算でも何とかなる範囲ではそんなに感動してもらえない損な役回りを押し付けられている)。
【初心者向け】線形関数や絶対値関数
- ところで同じ円に「誤差関数(ERF)の出力結果を射影(Projection)した結果(すなわち中心点から辺縁にかけて30本以上の波紋を発生させた結果)」も、ほぼ上掲の「正面図」と同じに見える。前者が「地平線/水平線(Horizon)までしか見通せない人間の視覚世界の限界」を示しているとすれば、後者は「(重力レンズ効果によって)球面の裏側まで見通せてしまうブラックホールの見え方」に該当する訳だが「15本目までの波紋」の挙動がほぼ同じな一方、16本目以降の挙動は周辺部でゴチャゴチャと瞬いてる様にしか映らないので観察者の主観が差分を勝手に「誤差として切り捨ててしまう」のである。実際ガウスは惑星観測の精度を上げるべく「誤差として切り捨てる範囲」を(主観者の恣意的補完でなく)しかるべき計算によって導出すべく誤差関数(ERF)を制定した訳で「三昧状態と無明状態の境界線」はかかる「隔壁落とし」のプロセスとしても現れてくる。
【初心者向け】誤差関数(ERF)と相補誤差関数 (ERFC)。
そして、こうした「コンピューターによる視覚化」プロセスが暴き出す「(観察者の主観による恣意的補正に守られた)粗雑な代数構造の世界」と「(コンピューターが実際に稼働している)純粋数理に立脚する代数構造の世界」のズレは、極座標系(Polar Coordinate System)とデカルト座標系(Cartesian Coordinate System)の狭間で新たな局面を迎えるのです。
ユークリッド空間(Euclidean Space)における次元設定
古典的なギリシャ数学では、ユークリッド平面や(三次元)ユークリッド空間は所定の公準によって定義され、そこからほかの性質が定理として演繹されるものであった。現代数学では、デカルト座標と解析幾何学の考え方にしたがってユークリッド空間を定義するほうが普通である。そうすれば、幾何学の問題に代数学や解析学の道具を持ち込んで調べることができるようになるし、三次元以上のユークリッド空間への一般化も容易になるといった利点が生まれる。
実にさりげなく「現代数学におけるパラダイムシフト」概念、すなわち「涅槃=(人間の脳でのみ稼働する)粗雑な代数構造」から「三昧=(コンピューター上でも稼働する)純粋数理に立脚する精緻な代数構造」への飛躍の話が挿入されてますね。
涅槃(サンスクリット語:निर्वाण、nirvāṇa=ニルヴァーナ) -Wikipedia
三昧(サンスクリット語: समाधि, ラテン文字転写: samādhi) -Wikipedia
そして…
ユークリッド次元Dに存在する線形サイズ1の図形があり、そのサイズを各空間方向に1/lに縮めると、もとの図形を埋めるにはN=l^D個の自己相似図形が必要となる。すなわちD=log(N,base=l)によって定義される次元はまだその位相次元もしくはユークリッド次元と等しい。
統計言語Rによる実証結果
# Log base=exp(1)の世界
> log(Inf)
[1] Inf
> log(1)
[1] 0
> log(0)
[1] -Inf
# -Infは計算出来ない(0にはならない)。
> log(-Inf)
[1] NaN
警告メッセージ:
log(-Inf) で: 計算結果が NaN になりました
> log(exp(1))
[1] 1
# Log base=1の世界
> log(Inf,base=1)
[1] Inf
# log(1,base=1)は計算出来ない。
> 1^1
[1] 1
> log(1,base=1)
[1] NaN
警告メッセージ:
計算結果が NaN になりました
> log(0,base=1)
[1] -Inf
# やはり逆は計算出来ない(0にはならない)。
> log(-Inf,base=1)
[1] NaN
警告メッセージ:
計算結果が NaN になりました
# Log base=2の世界
> log(Inf,base=2)
[1] Inf
> log(1,base=2)
[1] 0
> log(0,base=2)
[1] -Inf
# やはり逆は計算出来ない(0にはならない)。
> log(-Inf,base=2)
[1] NaN
警告メッセージ:
計算結果が NaN になりました
# 1次元
> 2^1
[1] 2
> log(2,base=2)
[1] 1
# 2次元
> 2^2
[1] 4
> log(4,base=2)
[1] 2
# 3次元
> 2^3
[1] 8
> log(8,base=2)
[1] 3
# Log base=3の世界
> log(Inf,base=3)
[1] Inf
> log(1,base=3)
[1] 0
> log(0,base=3)
[1] -Inf
# やはり逆は計算出来ない(0にはならない)。
> log(-Inf,base=3)
[1] NaN
警告メッセージ:
計算結果が NaN になりました
# 1次元
> 3^1
[1] 3
> log(3,base=3)
[1] 1
# 2次元
> 3^2
[1] 9
> log(9,base=3)
[1] 2
# 3次元
> 3^3
[1] 27
> log(27,base=3)
[1] 3
おや? ユークリッド空間において次元数算出を担う指数・対数関数(Exponential/Logarithmic Function)は「次元数1(すなわち底=1,真数=自然数集合)」の世界において真数1の場合に、思わぬ挙動不審状態に陥る様です。
【Yahoo知恵袋】高校数学の対数で、なぜ底が1ではいけないのでしょうか?
それはそれとして、こうして「次元数が整数値の」ユークリッド次元概念の定義から出発する「次元数が非整数値の」フラクタル次元の世界はともかく(そちらは怖過ぎるので当面「遊泳禁止区域」に設定する)、ユークリッド空間(Euclidean Space)は座標系(Coodenate System)でもあり、そこでは単位図形(Unit Figure)は貼られる数だけ空間を1/N分割するのではなくN倍に広げるし、その際に偶奇性(Eveness)問題が発生したりするのです。
【初心者向け】偶奇性概念と共役関係概念の連続性について。

立体的には単なる同心円とも、大半径1,小半径1のトーラス構造とも表現し得る。


単位立方体(Unit Cube)と単位球面(Unit Shere)
まずは単位立方体(Unit Cube)の生成関数を設定。
library(rgl)
# 座標(Coordinate)合成関数cd
cd<-function(a,b,c){paste0("(",a,",",b,",",c,")")}
# mo(Minus One),cp(Center Point),po(Plus One)
cube_draw01<-function(m,c,p,scale){
if(scale){
# 頂点座標=8個
texts3d(m,m,m,texts=cd(m,m,m),col=rgb(0,0,0),adj=1.0)
texts3d(p,m,m,texts=cd(p,m,m),col=rgb(0,0,0),adj=1.0)
texts3d(m,p,m,texts=cd(m,p,m),col=rgb(0,0,0),adj=1.0)
texts3d(p,p,m,texts=cd(p,p,m),col=rgb(0,0,0),adj=1.0)
texts3d(m,m,p,texts=cd(m,m,p),col=rgb(0,0,0),adj=1.0)
texts3d(p,m,p,texts=cd(p,m,p),col=rgb(0,0,0),adj=1.0)
texts3d(m,p,p,texts=cd(m,p,p),col=rgb(0,0,0),adj=1.0)
texts3d(p,p,p,texts=cd(p,p,p),col=rgb(0,0,0),adj=1.0)
# 頂点間中点=1+6+12=19個
texts3d(c,c,c,texts=cd(c,c,c),col=c(200,200,200),adj=1.0,cex=0.5)
texts3d(m,c,c,texts=cd(m,c,c),col=c(200,200,200),adj=1.0,cex=0.5)
texts3d(c,m,c,texts=cd(c,m,c),col=c(200,200,200),adj=1.0,cex=0.5)
texts3d(c,c,m,texts=cd(c,c,m),col=c(200,200,200),adj=1.0,cex=0.5)
texts3d(p,c,c,texts=cd(p,c,c),col=c(200,200,200),adj=1.0,cex=0.5)
texts3d(c,p,c,texts=cd(c,p,c),col=c(200,200,200),adj=1.0,cex=0.5)
texts3d(c,c,p,texts=cd(c,c,p),col=c(200,200,200),adj=1.0,cex=0.5)
texts3d(c,m,m,texts=cd(c,m,m),col=c(200,200,200),adj=1.0,cex=0.5)
texts3d(c,m,p,texts=cd(c,m,p),col=c(200,200,200),adj=1.0,cex=0.5)
texts3d(c,p,m,texts=cd(c,p,m),col=c(200,200,200),adj=1.0,cex=0.5)
texts3d(c,p,p,texts=cd(c,p,p),col=c(200,200,200),adj=1.0,cex=0.5)
texts3d(m,c,m,texts=cd(m,c,m),col=c(200,200,200),adj=1.0,cex=0.5)
texts3d(m,c,p,texts=cd(m,c,p),col=c(200,200,200),adj=1.0,cex=0.5)
texts3d(p,c,m,texts=cd(p,c,m),col=c(200,200,200),adj=1.0,cex=0.5)
texts3d(p,c,p,texts=cd(p,c,p),col=c(200,200,200),adj=1.0,cex=0.5)
texts3d(m,m,c,texts=cd(m,m,c),col=c(200,200,200),adj=1.0,cex=0.5)
texts3d(m,p,c,texts=cd(m,p,c),col=c(200,200,200),adj=1.0,cex=0.5)
texts3d(p,m,c,texts=cd(p,m,c),col=c(200,200,200),adj=1.0,cex=0.5)
texts3d(p,p,c,texts=cd(p,p,c),col=c(200,200,200),adj=1.0,cex=0.5)
# 平方対角線(長さsqrt(2))=6面*2=12本
lines3d(c(m,p),c(m,p),c(m,m),col=rgb(0,1,0),lwd=1)
lines3d(c(m,p),c(p,m),c(m,m),col=rgb(0,1,0),lwd=1)
lines3d(c(m,p),c(m,p),c(p,p),col=rgb(0,1,0),lwd=1)
lines3d(c(m,m),c(m,p),c(m,p),col=rgb(0,1,0),lwd=1)
lines3d(c(m,p),c(p,m),c(p,p),col=rgb(0,1,0),lwd=1)
lines3d(c(m,m),c(m,p),c(p,m),col=rgb(0,1,0),lwd=1)
lines3d(c(m,p),c(m,m),c(m,p),col=rgb(0,1,0),lwd=1)
lines3d(c(m,p),c(m,m),c(p,m),col=rgb(0,1,0),lwd=1)
lines3d(c(p,p),c(m,p),c(p,m),col=rgb(0,1,0),lwd=1)
lines3d(c(p,p),c(m,p),c(m,p),col=rgb(0,1,0),lwd=1)
lines3d(c(m,p),c(p,p),c(p,m),col=rgb(0,1,0),lwd=1)
lines3d(c(m,p),c(p,p),c(m,p),col=rgb(0,1,0),lwd=1)
}
# 正六面体(Square)本体=6面
lines3d(c(m,p,p,m,m),c(m,m,p,p,m),c(m,m,m,m,m),col=rgb(0,0,0),lwd=1)
lines3d(c(m,p,p,m,m),c(m,m,p,p,m),c(p,p,p,p,p),col=rgb(0,0,0),lwd=1)
lines3d(c(m,m),c(m,m),c(m,p),col=rgb(0,0,0),lwd=1)
lines3d(c(p,p),c(m,m),c(m,p),col=rgb(0,0,0),lwd=1)
lines3d(c(m,m),c(p,p),c(m,p),col=rgb(0,0,0),lwd=1)
lines3d(c(p,p),c(p,p),c(m,p),col=rgb(0,0,0),lwd=1)
# 頂点間中線=3+12=15本
lines3d(c(p,m),c(c,c),c(c,c),col=c(200,200,200),lwd=1)
lines3d(c(c,c),c(p,m),c(c,c),col=c(200,200,200),lwd=1)
lines3d(c(c,c),c(c,c),c(p,m),col=c(200,200,200),lwd=1)
lines3d(c(c,c,c,c,c),c(m,p,p,m,m),c(m,m,p,p,m),col=c(200,200,200),lwd=1)
lines3d(c(m,p,p,m,m),c(c,c,c,c,c),c(m,m,p,p,m),col=c(200,200,200),lwd=1)
lines3d(c(m,p,p,m,m),c(m,m,p,p,m),c(c,c,c,c,c),col=c(200,200,200),lwd=1)
# 立方対角線(長さsqrt(3))=4本
lines3d(c(m,p),c(m,p),c(m,p),col=rgb(0,0,1),lwd=1)
lines3d(c(m,p),c(p,m),c(p,m),col=rgb(1,0,0),lwd=1)
lines3d(c(m,p),c(p,m),c(m,p),col=rgb(1,0,0),lwd=1)
lines3d(c(m,p),c(m,p),c(p,m),col=rgb(1,0,0),lwd=1)
}
そして半径1の単位球面(Unit Sphere)概念から出発します。
【初心者向け】「単位円筒」から「単位球面」へ

これに対応するのは、とりあえず一辺2の立方体(Cube)となりますね。
偶数系
【オイラーの多面体定理と正多面体】とある「球面幾何学」の出発点…

X={-1,1},Y={-1,1}の範囲

cube_draw01(-1,0,1,TRUE)
# アニメーション
movie3d(spin3d(axis=c(0,0,1),rpm=5),duration=10,fps=25,movie="~/Desktop/cube003")
cube_draw01(-2,0,2,FALSE)
cube_draw01(-1,0,1,TRUE)
# アニメーション
movie3d(spin3d(axis=c(0,0,1),rpm=5),duration=10,fps=25,movie="~/Desktop/cube006")
奇数系
【オイラーの多面体定理と正多面体】とある「球面幾何学」の出発点…
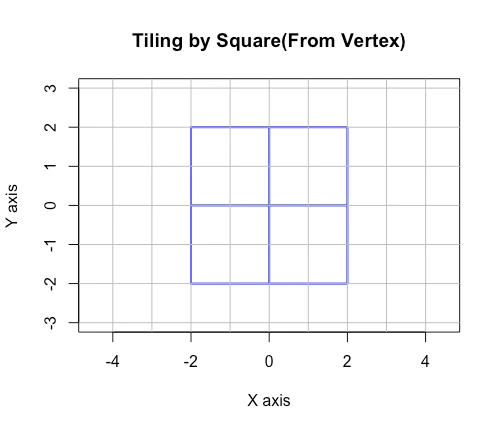
X={0,2},Y={0,2}の範囲

cube_draw01(0,1,2,TRUE)
# アニメーション
movie3d(spin3d(axis=c(0,0,1),rpm=5),duration=10,fps=25,movie="~/Desktop/cube007")
cube_draw01(-2,0,2,FALSE)
cube_draw01(-2,-1,0,TRUE)
cube_draw01(0,1,2,TRUE)
# アニメーション
movie3d(spin3d(axis=c(0,0,1),rpm=5),duration=10,fps=25,movie="~/Desktop/cube009")
おや、何か違和感がありますね。そう、普段見慣れているデカルト座標系(Cartesian Coordinate System)における考え方はこうではないからです。
デカルト座標系(Cartesian Coordinate System)における単位立方体(Unit Cube)
デカルト座標系は上掲の表現を用いると「奇数系」に該当し、その空間をとりあえず埋め尽くすのは1辺が距離1の単位立方体(Unit Cube)となります。
X={0,1},Y={0,1}の範囲での平方対角線と立方対角線

cube_draw01(0,0.5,1,TRUE)
# アニメーション
movie3d(spin3d(axis=c(0,0,1),rpm=5),duration=10,fps=25,movie="~/Desktop/cube001")
X={-1,1},Y={-1,1}の範囲での平方対角線と立方対角線

cube_draw01(-1,0,1,FALSE)
cube_draw01(-1,-0.5,0,TRUE)
cube_draw01(0,0.5,1,TRUE)
# アニメーション
movie3d(spin3d(axis=c(0,0,1),rpm=5),duration=10,fps=25,movie="~/Desktop/cube005")
つまり半径1の単位円1個に一辺1の単位立方体8個が対応する換算…どうもこの辺りに何らかの形で「隔壁」が落とされた気配がします。詳細は以下続報…





