ただ単にピタゴラスの定理(Pythagorean Theorem)r(半径)=sqrt(x(x軸上の値)^2+y(y軸上の値)^2+z(z軸上の値)^2+…)(ただしr=x=y=z…)が描くN次元の直線/円/球を拡張しただけでは「半径が1なら直径は2」という結論に到達し得ません。
【初心者向け】ピタゴラスの定理あるいは三平方の定理からの出発
- 1次元(直線):r=sqrt(x^2)=x(ただしr=x)
- 2次元(円弧):r=sqrt(x^2+y^2)(ただしr=x=y)
- 3次元(球面):r=sqrt(x^2+y^2+z^2)(ただしr=x=y=z)
理由は簡単、両者の間には「そのままでは超えられない壁」が横たわっているからです。
【Rで球面幾何学】等差数列(算術数列)②数直線概念から同心円集合概念へ
-
半径(Raduus)が構成するのは片側無限算術数列(One-Sided Infinite Sequence)

-
直径(Diameter)が構成するのは両側無限算術数列(both-Sided Infinite Sequence)。直線x=0を軸線に選んだ場合
(xの値の推移は-1から+1に及ぶが、Yの値は0以下/0以上に留まる)。
-
直線y=0を軸線に選んだ場合
(yの値の推移は-1から+1に及ぶが、xの値は0以下/0以上に留まる)。
そう、私が数年前から本腰を入れ始めた数理(Mathematical Things)方面からのアプローチは何と「1+1=2」の部分でつまづいてしまったのです。
回避不可能の「デカルト座標系」実存問題
こここでいう「超えられない壁」の正体は「デカルト座標系(Cartesian Coordination)=互いに直交するN次元評価軸」を前提としてるか否か。
直交座標系 - Wikipedia
-
そもそも上掲式を眺めても明らかな様に、ピタゴラスの定理自体にデカルト座標系(Cartesian Coordinate System)、すなわち「互いに直交する」=統計学でいうところの相関係数(Correlation Coefficient)0の状態の尺度が連続するN次元評価軸(N-Dimensional Evaluation Axis)が構成する直交座標系概念(Orthogonal Coordinate System Concept)の実存を前提とする側面が存在する。
相関係数 - Wikipedia
-
実は「ハミルトンの四元数(Hamilton's Quaternion)=球面上に位置する原蹠と対蹠の間を2回直角に曲がって結ぶ3次元系の空間処理概念」も同じ問題を抱えていたりする。
【Rで球面幾何学】ハミルトンの四元数は何を表しているのか?
さてこの問題、一体どういう風に解けば良いのでしょう?
そもそも「それ」は人類の発明品なんかじゃなかった?
数年間この問題について頭を悩ませ続けた結果、私は純粋な数理(Mathematical Things)方面からのアプローチを諦め「そもそもデカルト座標系は人間が発明したものじゃない(おそらくはピタゴラスの定理の大源流も)」と考える様になりました。
- それなら我々の時空間認識、すなわち時間経過(過去・現在・未来)+二次元(X軸+Y軸、例えば「前方・中央・後方」と「左方・中央・右方」の「中央」を原点とする直交)あるいは三次元(X軸+Y軸+Z軸、例えば「前方・中央・後方」と「左方・中央・右方」と「上方・中央・下方」の「中央」を原点とする直交)といった感覚は何に由来するのか?
- どう考えても「地上に誕生した生物の末裔として継承したこの身体の使用感」に由来すると考えるしかないのではあるまいか?
Humanity(人間中心主義)どころの話じゃありません。何しろその起源はカンブリア爆発期(Cambrian Explosion、葯5億4200万年前〜5億3000万年前)まで遡る訳ですから。
カンブリア爆発(Cambrian Explosion) - Wikipedia
- その頃より視覚と関連情報を処理する脊髄=中央情報処理器官(Central Infomation Processing Organ)」を獲得する事で前後上下左右といった空間感覚と時間の前後感覚を獲得し(四肢に該当する何らかの器官を備えて制御する事で)比較的俊敏な動作をこなす様になった左右相称動物(Bilateria)が、トレンドに乗り遅れ相変わらず鈍重なままのクラゲやヒトデの様な放射相称動物(Radiata)に進化面で優位に立ち始めた。少なくとも「デカルト座標系(Cartesian Coordination)=互いに直交するN次元評価軸」や、これに立脚して「観測は試行回数分だけの観測結果によって成立する」といった経験則に基づいて状況を把握する能力は、それ以前の時代まで遡れない。
左右相称動物
放射相称動物 - 一方、この時代にはかかる新能力を初めて捕食動物として有効活用し、一旦は「(当時の生物としては破格の大きさまで成長した)地球最初の百獣の王」アノマロカリス(Anomalocaris、約5億2,500万〜約5億0,500万年前)が登場し、最後には遺伝子的痕跡を後世に一切残す事なく潔く滅び去っている。そもそもどうしてこの生物は滅びたのか。ある考え方に従えば、皮肉にもこの捕食性動物は、その奇跡的成長ゆえに「(棘や殻や毒で自衛した)食えない連中」ばかり淘汰して狩果を先細らせる一方、原始的な魚類の先祖といった競争相手の進化ラッシュを引き起こしてしまったのだという。その感点から「あらゆるビジネスモデル(および歴史的事象)の先例」と皮肉る向きもある。
アノマロカリス(Anomalocaris)-Wikipedia - またこの生物には恐らく自らの身体の世界に対する相対的成長(巨大化)を認識する能力が欠落しており、それで時間経過に従って世界がどんどん小さくなっていく様にしか感じられなかった。この問題は案外難しく、それを回避するにはおそらく無限遠点(Infinity)を時空間概念の極限に設定した数理概念などを備えなければならないが、生物が曲がりなりにもそれを備えたのは一体いつの段階だったのか?
生物が大量絶滅から復活するまでの時間はわずか「2~3年」だった!
こうして新たに「デカルト座標系以前」から存在し得る(すなわち数理として完全に独立しており、理論上は植物や放射相称動物でも備え得る)数理の範囲を明かにする旅が始まった訳ですが、実はそれはそれ以降にしか存在し得ない数理の範囲を明かにするプロセスでもあったのです。
-
連続尺度の従属変数(目的変数)Y と独立変数(説明変数)Xの間にモデルを当てはめる(Xが1次元ならば単回帰, Xが2次元以上ならば重回帰, Yが離散の場合は分類という)回帰分析(Regression Analysis)。
回帰分析 - Wikipedia - データから(プライオリティ付けした)N次元評価軸を抽出する因子分析(Factor Analysis)。乱数を与えてもこれを遂行する著名で完全には克服不可能なバグがある。
因子分析 - Wikipedia - 相関のある多数の変数から相関のない少数で全体のばらつきを最もよく表す主成分と呼ばれる変数を合成しデータ次元を削減する主成分分析(Principal Component Analysis; PCA)。
主成分分析 - Wikipedia
MCMC(Markov chain Monte Carlo methods=マルコフ連鎖モンテカルロ法)には、この制約を乗り越える力がある?
【初心者向け】「モンテカルロ法」概説 - Qiita

いずれにせよ「素早く力強く確実に動く方向への進化」だけが全てではないのが適者生存世界のややこしいところ。
【初心者向け】ロジスティック方程式とその関連範囲 - Qiita

「カンブリア期の贈り物」は祝福にして呪縛?
こうして我々が継承した「(デカルト座標系の大源流に存在する)時間経過及び前後上下左右を峻別する空間認識能力」には、同時に「実世界で体感可能な事」以上をイメージしようとすると途端に虚無の壁に突き当たり「途方に暮れてしまう=それが何か途端にイメージ出来なくなってしまう」欠陥も存在します。
- 例えば「正方形(Square)=円弧上の1点より直角に3回曲がって原点に到達する軌跡」を、同操作がx軸-y軸,x軸-z軸,y軸-z軸の三軸全てにおいて成立する様に調整すると、結果として「正方形を2枚直角に重ねた」事になり正八面体(Regular Octahedron)が顕現する(あくまで、あらかじめ「直角とは何か」判っている事が前提となるが、もしかしたらこれこそが我々が最小限の努力でデカルト座標の概念に到達する方法論かもしれない)。実はこの操作はN次元に渡って再帰的に積み重ねていけるが、我々の生得的時空間認識能力はそこで限界に到達し「途方に暮れてしまう」のである。
【オイラーの多面体定理と正多面体】とある「球面幾何学」の出発点…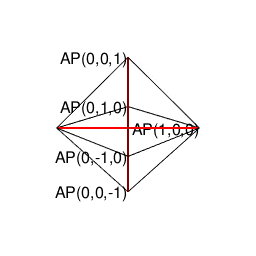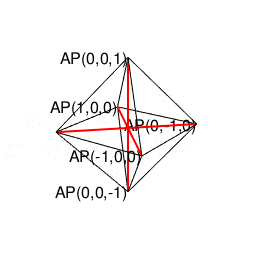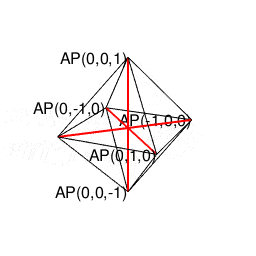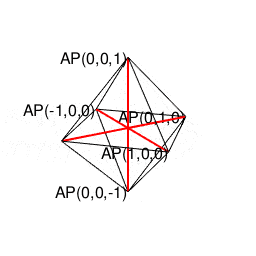
ところで本当に「視覚とその情報を処理する脊髄」の獲得に始まり、遂には「デカルト座標系」獲得に至った我々の歴史は、本当に放射相称動物全般に対する完全勝利だったのでしょうか? その辺りに関する実存不安こそが「外世界よりやってくる異質な侵略者の多くが(人類の様に二眼でなく)三眼や五眼や七眼である」問題の回答なのかもしれません。
(人類の限界を乗り越えんとする)N進法/p進数の世界?
