全ての計算を人力に頼るしかなかった近世までの数学の世界では、計算量削減の為に関心範囲を「二項モデル(Binomial Model)」に集中させる傾向が顕著に見られました。
- 「二項定理(Binomial Theorem)」…「パスカルの三角形(Pascalian Triangle)」の数式化。
【Python演算処理】パスカルの三角形と二項定理または二項展開
二項定理を超わかりやすく解説(公式・証明・係数・問題) - 「二項分布(Binomial Distribution))」…ベルヌーイ試行(結果が成功か失敗の2値で表される試行)を独立にn回行った時の成功回数を確率変数xとする離散確率分布(ただし各試行における成功確率pは一定とする)。
二項分布 - Wikipedia - 「二項係数(Binomial Coefficients)」… 上掲二つの概念の背後に共通して存在する数理。
二項係数 - Wikipedia
二項係数の有名公式一覧と2つの証明方針|高校数学の美しい物語
そしてかかる偏った方針は近代以降の数学に思わぬ形で影を落とす事になったのです。
「二項関係」と「順列」および「組み合わせ」
とある集合Sから、集合Sの要素を2つ並べたものを何個か集めた集合(集合論的表現では「Sの部分集合」)を二項関係と言います。
- 例えば集合$S=(1,2,3,…,n)$の直積$S×S$の場合はその部分集合((1.2),(2.3)),((2,1),(3,2),(2,1)),((2,2)),$\phi$(空集合)などが二項関係となる。
| 1 | 2 | 3 | … | n | |
|---|---|---|---|---|---|
| 1 | (1,1) | (1,2) | (1,3) | … | (1,n) |
| 2 | (2,1) | (2,2) | (2,3) | … | (2,n) |
| 3 | (3,1) | (3,2) | (3,3) | … | (3,n) |
| … | … | … | … | … | … |
| n | (n,1) | (n,2) | (n,3) | … | (n,n) |
import numpy as np
import sympy as sp
import pandas as pd
X1 = np.matrix([
["(1,1)","(1,2)","(1,3)","…","(1,n)"],
["(2,1)","(2,2)","(2,3)","…","(2,n)"],
["(3,1)","(3,2)","(3,3)","…","(3,n)"],
["…","…","…","…","…"],
["(n,1)","(n,2)","(n,3)","…","(n,n)"]])
# x=X1.transpose()
x=X1
df=pd.DataFrame(x,columns=['1','2','3','…','n'],index=['1','2','3','…','n'])
sp.init_printing()
org=df.to_html()
print(org.replace('\n', ''))
- 集合$S_n=(1,2,3,…,n)$の要素数はn個。
- 直積集合$S_n×S_n$の要素数**は$n^2$個。
- 冪集合$2^{S_n}$の要素数は$2^n$個(n個の要素に対する選ぶか選ばないかの2択)。
- 集合Sの二項関係の総数は直積集合$S_n×S_n$の部分集合の総数に一致するが、それぞれの要素について選ぶか選ばないかの2択が発生するので$2^{n^2}$個となる。
- 直積集合の直積集合$(S_n×S_n)×(S_n×S_n)$の要素数は$n^2×n^2$となるので$n^4$となる。
- 直積集合$S_n×S_n$の二項関係の総数は直積集合の直積集合$(S_n×S_n)×(S_n×S_n)$の部分集合の総数と一致するが、それぞれの要素について選ぶか選ばないかの2択が発生するので$2^{n^4}$個となる。
「比較可能性」と「完全関係」
集合の範囲内で任意の数2つx,yを選んだ場合、その数そのままかx,yを入れ替えると必ず関係を満たす要素だけを集めた部分集合を「比較可能性(Comparability)がある」あるいは「完全関係(Total Relation)にある」と表現する。
\forall x, \forall y \in A,\ x R y \lor y R x((x,y) \in R \lor (y,x) \in R)
上掲の直積集合$(S_n×S_n)×(S_n×S_n)$でいうと以下の組が該当。
- (1,1),(2,2),(3,3),(n,n)=以下に述べる同値条件の反射律に対応。行列演算でいう「対角要素」に該当。
- (1,2)⇄(2,1)…行列演算でいう「転置関係」に該当。
- (1,3)⇄(3,1)…同上。
- (2,3)⇄(3,2)…同上。
- (1,n)⇄(n,1)…同上。(1,1),(1,2)⇄(2,1),(1,3)⇄(3,1)を含む。
- (2,n)⇄(n,2)…同上。(2,2),(2,1)⇄(1,2),(2,3)⇄(3,2)を含む。
- (3,n)⇄(n,3)…同上。(3,3),(3,1)⇄(1,3),(3,2)⇄(2,3)を含む。
ここにはいわゆる「組み合わせ論」との対応がうかがえます。
4つの数から2つの数の組み合わせを選ぶ方法は $\tbinom {4}{2}=6$通り。x,yの入れ替えを含める順列だと12通り。
\begin{bmatrix}
1,1 & 1,2 & 1,3 & 1,4\\
2,1 & 2,2 & 2,3 & 2,4\\
3,1 & 3,2 & 3,3 & 3,4\\
4,1 & 4,2 & 4,3 & 4,4\\
\end{bmatrix}
- 2つの数から2つの数の組み合わせを選ぶなら$\tbinom {2}{2}=1$通り。x,yの入れ替えを含めた順列では(1,2)(2,1)の2通り。
\begin{bmatrix}
1,1 & 1,2 \\
2,1 & 2,2
\end{bmatrix}
- 3つの数から2つの数の組み合わせを選ぶなら$\tbinom {3}{2}=3$通り。x,yの入れ替えを含めた順列では(1,2)(2,1)(2,3)(3,2)(1,3)(3,1)の6通り。
\begin{bmatrix}
1,1 & 1,2 & 1,3\\
2,1 & 2,2 & 2,3\\
3,1 & 3,2 & 3,3
\end{bmatrix}
直積集合$(S_n×S_n)×(S_n×S_n)$から要素数$n^2$-対角成分nを得る演算は(異なるn個の中から異なるr個を取り出して1列に並べる)順列(Sequence Without Repetition)$nPr=n!/(n-r)!$の計算に対応する。
import math as m
def set_count(n):
return n**2-n
def permutations_count(n, r):
return m.factorial(n) // m.factorial(n - r)
# 出力結果
print(set_count(2))
print(permutations_count(2, 2))
print(set_count(3))
print(permutations_count(3, 2))
print(set_count(4))
print(permutations_count(4, 2))
print(set_count(5))
print(permutations_count(5, 2))
出力結果
2
2
6
6
12
12
20
20
直積集合$(S_n×S_n)×(S_n×S_n)$から$\frac{要素数n^2-対角成分n}{2}$を得る演算は(異なるn個の中から異なるr個を取り出して1列に並べる)組み合わせ(Combination)$nCr=nPr/r!$あるいは$n!/(r!×(n−r)!)$の計算に対応する。
import math as m
def set_count(n):
return int((n**2-n)/2)
def combinations_count(n, r):
return m.factorial(n) // (m.factorial(n - r) * m.factorial(r))
# 出力結果
print(set_count(2))
print(combinations_count(2, 2))
print(set_count(3))
print(combinations_count(3, 2))
print(set_count(4))
print(combinations_count(4, 2))
print(set_count(5))
print(combinations_count(5, 2))
出力結果
1
1
3
3
6
6
10
10
「平行な直線の方程式」と「同値関係」
中高生レベルの数学からの再出発です。
「平行な直線の方程式」
2つの直線$y=m_1x+n_1,y=m_2x+n_2$について、2直線が平行であることと傾き$m_1=m_2$であることは同値である。
同値関係(Equivalence Relation) -Wikipedia
ある集合Sを、その任意の元a,b,cについて同値類(Equivalence Class)[a][b][c]に分割する2項関係。a,b,cが同じ同値類に属するのはそれぞれ同値関係(Equivalence Relation)$\sim$である場合、かつその場合のみに限られる。
- [a]=$(x \in S \mid x \sim a)$
- [b]=$(x \in S \mid x \sim b)$
- [c]=$(x \in S \mid x \sim c)$
同値関係の具体例としてしばしば以下が列記される。
- 相等関係(=):集合としてあるいは集合の元として同じである。表現形式や構成要素が同一である。
- 図形の合同関係:位置や裏表や向きの違いを無視して、図形として同じである。
- 図形の相似関係:裏表・向き・大きさの比率の違いを無視して、図形の "形" としては同じである。
- 量の比例関係:増え方・減り方の割合としては同じである。
- 整数の合同関係:ある数で割った余りが同じである。
定義としては$(\forall a,b,c \in S)$、すなわちある集合Sの任意の元a,b,cの二項関係において以下の同値律が全て成立する場合を同値という。
①反射律:a∼a.
反射関係(Reflexive Relation) -Wikipedia
反射的関係$R_1=(\forall a\in X,\ aRa).$
X の全ての元 a について、a が自分自身とRの関係を持つ。
無射的関係$R_2=(\forall a\in X,\ \lnot (aRa)).$
X の全ての元 a について、a が決して自分自身とRの関係を持たない。
| 反射関係(Reflexive Relation) | 無反射性(Irreflexive Relation) | |
|---|---|---|
| 0 | A=B(等式) | A≠B |
| 1 | A∈B(集合の包含関係) | A∉ B |
| 2 | AはBで割り切れる(約数) | AはBと互いに素である |
| 3 | A≧B/A≦B | A>B/A<B |
import numpy as np
import sympy as sp
import pandas as pd
X1 = np.matrix([
["A=B(等式)","A∈ B(集合の包含関係)","AはBで割り切れる(約数)","A≧B/A≦B"],
["A≠B","A∉B","AはBと互いに素である","A>B/A<B"]])
x=X1.transpose()
df=pd.DataFrame(x,columns=['反射関係(Reflexive Relation)', '無反射性(Irreflexive Relation)'])
sp.init_printing()
org=df.to_html()
print(org.replace('\n', ''))
- 例えば0を含む2つの半開集合(半開区間)$S^1_{n^-}(n^-≦0)$と$S^1_{n^+}(n^+≧0)$は反射関係を構築するが、0を含まない2つの開集合(開区間)$S^2_{n^-}(n^-<0)$と$S^2_{n^+}(n^+>0)$は**反射関係**を構築せず**無反射関係**となる(別の表現では「不等式“less than or equal to”や“greater than or equal to”は反射的だが、“less than”や“greater than”は無反射的」)。
開集合 - Wikipedia - なお無反射性は反射性の不成立条件より狭い範囲に適用されるので、関係の全てが反射的なものと無反射的なものに分類されるわけではない。従って、二項関係は、反射的なもの、無反射的なもの、どちらでもないものに分類される。
②対称律:a∼bならばb∼a.
うさぎでもわかる離散数学 第4羽 二項関係編
対称関係$(x,y) \in R \to (y,x) \in R$

反対称関係$\forall x, \forall y \in A,\ x R y \land y R x \to x = y$

対称関係(Symmetric Relation) -Wikipedia
対称関係$R=(\forall a,b\in X,\ aRb\Rightarrow ;bRa)$
Xに属する全てのaおよびbについて、aRbが成り立つならbRaも成り立つ。
ただし対称関係と反対称関係(aRbかつbRaならばb=a)は正確には反対の意味ではない。
- 「等号」は対称的かつ反対称的でもある。
- 「約数」は対称的でも反対称的でもない。
- 「合同式(大雑把に言うと割り算の余りのみに注目した等式)における合同関係」は対称的だが反対称的ではない。
合同式(mod)の意味とよく使う6つの性質|高校数学の美しい物語 - 「≦や≧」は対称的ではないが反対称的ではある。
③推移律:a∼bかつb∼cならばa∼c.
うさぎでもわかる離散数学 第4羽 二項関係編
推移関係$\forall x, \forall y, \forall z \in A,\ x R y \land y R z \to x R z$
あるいは$(x,y) \in R \land (y,z) \in R \to(x,z) \in R$

- まさしく「数学的に用法がかなり厳格化された三段論法」という捉え方。
三段論法 - Wikipedia
推移関係(Transitive Relation) -Wikipedia
推移関係$R=\forall a,b,c\in X,\ a,R,b\land b,R,c;\Rightarrow a,R,c)$
Xの任意の元a、b、cについて、aとbにRが成り立ち、bとcにRが成り立つ時、aとcにもRが成り立つ。
- 「A=B(等式)」はa=bでかつb=cであればa=cが成り立つので推移関係である。
- 「$A \in B$(集合の包含関係)」は$a \in b$でかつ$b \in c$であれば$a \in c$が成り立つので推移関係である。
- 「$A<B$,$A \leqq B$,$A<B$,$A \geqq B$(不等式)」も推移関係である。
- 「AはBで割り切れる」(約数)も推移関係である。
- 「AならばBである(含意)」も推移関係である。
- 集合に少なくとも2つ以上の元がある場合「$A \neq B$」は非推移関係である。
ところで、ここで反射性との関係に目を向けると…
【順序集合】反射性/非反射性と対称性/非対称性と推移性/非推移性の関係定義
かかる諸概念こそが群論(Group Theory)における群同型(Group Isomorphism)概念や準同型写像(Group Homomorphism)概念の出発点となる訳です。
抽象代数学における2つの群の間の関数。与えられた群演算と両立する方法で群の元の間の一対一対応を可能とする。2つの群の間に同型写像が存在すれば群は同型(isomorphic)と呼ばれ「群論の見地からは」同型な群は同じ性質を持っており、区別する必要はないとされる。
数学、特に群論において群の構造を保つ写像。準同型写像は単に準同型とも呼ばれる。
- hは、群G(左)から群H(右)への群準同型。H内の楕円はhの像。Nはhの核。aNはhの属する剰余類。
ふたつの群(G,∗)と(H,⋅) が与えられたとする。
(G,∗)から(H,⋅) への群準同型は写像h: G→H となり、$h(u*v)=h(u)\cdot h(v)\qquad (\forall u,v\in G)$の条件を満たす。
ここで、左辺はGの元に対してGの群演算を施したものをhで写した先のHの元を意味し、右辺は Gの各元をhでHの元に写したものにHの群演算を施したものである。
その定義から準同型写像hは、Gの単位元eGをHの単位元eHに写し、また$h(u^{-1})=h(u)^{-1}$が成り立つという意味で逆元を逆元に写す事も示す。このとき、「hは群構造と両立する(compatible with)」ともいう。
- この次元においてやっと、状況に応じて「加法実数群を水平軸、乗法実数群を垂直軸に取って両者の間を対数・指数写像によって往復する円筒座標系(半径1の時、その傾きは実数列そのものとなる)」とも「赤道を半径1の単位円、対蹠それぞれに観測原点0と観測限界∞を射映したリーマン球面(垂直軸に対数尺が振られるのが特徴)」とも表現可能な実数環(Real Ring)の世界が視野内に立ち現れる。
【Python演算処理】環論に立脚した全体像再構築①空環と実数環 - その幾何学的イメージがジェットコースターの如く苛烈に変遷し続けるので、むしろ群論的抽象化による全体像の把握に魅力を覚える様になる。なるほど、これが「ブルバキの見た世界」という訳か…
ニコラ・ブルバキ - Wikipedia
全体を貫くのは「同じであるとはどういう事か、そうでない状態をどう分類するか」鋭く峻別しつつ抽象化を進めていく研究姿勢。圏論(Category Theory)ではさらに核家族$S_1$の妻$S_1^{0f}$と核家族$S_2$の妻$S_2^{0f}$まで厳格に峻別して扱う様ですが、この投稿ではそこまでは踏み込まないものとします。
「垂直な直線の方程式」と「円関数の微分」と「曲率」
改めて中高生レベルの数学からの再出発です。
「垂直な直線の方程式」
2つの直線$y=m_1x+n_1,y=m_2x+n_2$について、2直線が垂直である事と$m_1m_2=−1$である事は同値である。
①垂直に交わる2つの直線$y=m_1x+n_1,y=m_2x+n_2$があるとする。なお、y軸に平行な直線を$y=mx+n$の形で表すことは出来ないので、どちらの直線もx軸、y軸に平行ではないとする。

②$y=m_1x+n_1$と$y=m_1x$は平行で、$y=m_2x+n_2$と$y=m_2x$も平行なので、$y=m_1x+n_1,y=m_2x+n_2$が垂直である事と、$y=m_1x,y=m_2x$が垂直である事は同値となる。切片がない方が考えやすいので、以降は切片がない場合(上の図の青い直線)について考える。
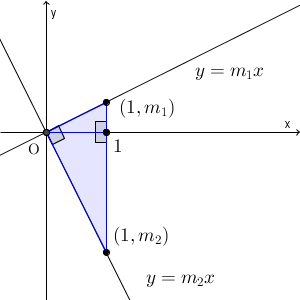
③$y=m_1x,y=m_2x$の2直線が垂直であると考えるなら$(1,m_1),(1,m_2),(0,0)$を結ぶと直角三角形が現れる。そこで三平方の定理を導入し各辺の長さの2乗を求めてみる。
- 斜辺については$(1,m_1),(1,m_2)$の2点のうち、どちらかがx軸より上、もう一方はx軸より下となるので斜辺の2乗は$(m_1−m_2)^2$となる。$(m_1+m_2)^2$ではない点に注意。上図であれば$m_2$は負となり、その為に斜辺のうちx軸より下の部分の長さは$−m_2$とマイナスがつく。
- 斜辺以外の2辺の長さの2乗は、$(1,0)$へ垂線をおろして考えれば、それぞれ$1+m_1^2,1+m_2^2$となる。
④よって、三平方の定理から2直線が垂直であれば、傾きの積が−1となる結果が得られる。
(m_1-m_2)^2=(1+m_1^2)+(1+m_2^2)\\
-2m_1m_2=2\\
m_1m_2=-1
⑤逆に$m_1m_2=−1$が成立する場合には上の式をそのまま逆に辿れば良い。$(m_1−m_2)^2=(1+m_1^2)+(1+m_2^2)$から$y=m_1x, y=m_2x$が垂直に交わる事が分かるので$y=m_1x+n_1,y=m_2x+n_2$も垂直に交わると分かる。
「円の方程式の微分」
陽関数y=f(x)の形で書けない陰関数はxを決めてもyがいつもただ1つに決まるとは限らず、その為「yはxの関数である」とはいえない。しかし、xの変化に応じてyがどのように変化するかは、場合分けをすれば調べることが出来る。ここでは円の方程式$x^2+y^2=1$について見ていこう。
①まずy>0の場合について考えると、円の方程式は$y=\sqrt{1−x^2}$の形に変形出来るので、これを$u=1−x^2,y=\sqrt{u}$なる合成関数の微分として解く。
\frac{dy}{dx}=\frac{dy}{du}\frac{du}{dx}\\
=\frac{1}{2}u^{\frac{1}{2}}(-2x)\\
=\frac{1}{2\sqrt{1−x^2}}(-2x)\\
=-\frac{x}{\sqrt{1−x^2}}
ここで分母がyと等しいので、微分した結果は$−\frac{x}{y}$と書く事が出来る。なおy=0の場合は微分出来ない。
②y<0の時も同じ様に計算して$−\frac{x}{y}$となるのでyの符号に拠らず以下の様に書ける。
\frac{dy}{dx}=−\frac{x}{y} (y≠0)
③円の方程式$x^2+y^2=1$の両辺をxで微分すると場合分けをしなくてもよくなる。これにより、右辺は0、左辺の$x^2$は$2x$となる。残った$y^2$の部分は合成関数の微分と考えると$2y \frac{dy}{dx}$と書けるので以下の計算が成立する。
2x+2y \frac{dy}{dx}=0\\
y \frac{dy}{dx}=-x\\
\frac{dy}{dx}=−\frac{x}{y} (y≠0)
ところで円の方程式$x^2+y^2=1$を微分して得られた$\frac{dy}{dx}=−\frac{x}{y} (y≠0)$には図形的にどんな意味があるのだろうか。
①$a,b>0,a^2+b^2=1$とし、点(a,b)での円の接線を考える。微分係数とはまさにこの接線の傾きそのものなので、先ほどの計算からその傾きは$-\frac{a}{b}$と定まる。


%matplotlib nbagg
import math as m
import cmath as c
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.animation as animation
# 単位円データ作成
c0=np.linspace(-m.pi,m.pi,61,endpoint = True)
s0=[]
for num in range(len(c0)):
s0.append(complex(m.cos(c0[num]),m.sin(c0[num])))
s1=np.array(s0)
# 垂直線
Vert_st0=complex(1,-5)
print(c.polar(Vert_st0))
print(abs(Vert_st0))
print(c.phase(Vert_st0))
Vert_ed0=complex(1,5)
plt.style.use('default')
fig = plt.figure()
# 関数定義
def unit_circle(n):
plt.cla()
#スポーク線描画
for num in range(len(s1)):
plt.plot([0,s1[num].real],[0,s1[num].imag],color="gray",lw=0.5);
#円周描画
plt.plot(s1.real,s1.imag,color="blue", label="Unit Cylinder")
plt.ylim([-1.1,1.1])
plt.xlim([-1.1,1.1])
plt.title("Unit Circle")
plt.xlabel("Real")
plt.ylabel("Imaginal")
ax = fig.add_subplot(111)
ax.set_aspect('equal', adjustable='box')
ax.legend(loc='upper right')
#補助線描画
plt.axvline(0, 0, 1,color="red")
plt.axhline(0, 0, 1,color="red")
#移動線描画
plt.plot([0,s1[n].real],[0,s1[n].imag],color="green",lw=1)
#垂直線
Vert_st=c.rect(abs(Vert_st0),c.phase(Vert_st0)+c0[n])
Vert_ed=c.rect(abs(Vert_ed0),c.phase(Vert_ed0)+c0[n])
plt.plot([Vert_st.real,Vert_ed.real],[Vert_st.imag,Vert_ed.imag],color="green",lw=1)
ani = animation.FuncAnimation(fig, unit_circle, interval=50,frames=len(s1))
ani.save("orth01.gif", writer="pillow")
②一方、この円の接線は図形的に「円の中心(0,0)と接点(a.b)を結ぶ直線」と垂直に交わるが、その傾きは$\frac{b}{a}$となり、両者の傾きの積が-1となる事からも両直線が垂直に交わっている事が証明されるのであった。
つまり、円の方程式を微分する事は、半径と垂直に交わる直線の傾きを求めるのと同値なのである。
また実際の微分結果に注目し、以下の様な考察を導出する事も可能である。
(y=)f(x)=\sqrt{1 - x^{2}}\\
f^{\prime}(x)=- \frac{x}{\sqrt{1 - x^{2}}}(=-\frac{x}{y})\\
f^{\prime\prime}(x)=- \frac{1}{\left(1 - x^{2}\right)^{\frac{3}{2}}}
import sympy as sp
x= sp.symbols("x")
# Rows
f0=sp.sqrt(1-x**2)
f1=sp.diff(f0,x,1)
f2=sp.diff(f0,x,2)
k=f2/((1+f1**2)**sp.Rational(3,2))
# Columns
sp.init_printing()
display(f0)
print("f(x)="+sp.latex(f0))
display(sp.simplify(f1))
print("f^{\prime}(x)="+sp.latex(sp.simplify(f1)))
display(sp.simplify(f2))
print("f^{\prime\prime}(x)="+sp.latex(sp.simplify(f2)))
# display(sp.simplify(k))
# print("\kappa ="+sp.latex(sp.simplify(k)))
- $y=\sqrt{1-x^2}$は半円関数
- これを微分した$y=\frac{x}{\sqrt{1 - x^{2}}}$はy(-∞→0→+∞),x(-1→0→+1)の範囲、さらにこれをXY転置した$x=\frac{y}{\sqrt{1 - y^{2}}}$はy(-1→0→+1),x(-∞→0→+∞)の範囲に射影されて(累積分布を連想させる)原点0を変曲点(Inflection Point)とするシグモイド曲線(Sigmoid)を描く。
シグモイド - Wikipedia

import sympy as sp
import numpy as np
import pandas as pd
from scipy import stats
import matplotlib.pyplot as plt
# 等差数列を生成
x = np.linspace(1,-1,61,endpoint = True)
y1 = np.sqrt(1-x**2)
y2 = -x/np.sqrt(1-x**2)
# pdfで確率密度関数を生成
plt.style.use('default')
fig = plt.figure()
# 可視化
plt.plot(x, y1,color="blue", label="y=f(x)=sqrt(1-x^2)")
plt.plot(x, -y1,color="red", label="y=-f(x)=-sqrt(1-x^2)")
plt.plot(x, y2,color="skyblue", label="y=f'(x)=-x/sqrt(1-x^2)")
plt.plot(x, -y2,color="orange", label="y=-f'(x)=x/sqrt(1-x^2)")
plt.plot(y2, x,color="lightgreen", label="x=f'(y)=-y/sqrt(1-y^2)")
plt.plot(-y2, x,color="darkgreen", label="x=-f'(y)=y/sqrt(1-y^2)")
plt.ylim([-4,4])
plt.xlim([-4,4])
plt.xlabel("x")
plt.ylabel("y")
plt.title("Circular Function")
ax = fig.add_subplot(111)
ax.set_aspect('equal')
ax.legend(loc='lower right')
plt.show()
- 一応二階微分した結果である$- \frac{1}{\left(1 - x^{2}\right)^{\frac{3}{2}}}$関数についても同様の場合を示しておくが、現時点ではこれに「凸関数の射影が凹関数に、凹関数の射影が凸関数に対応する」展開を説明する以上の意味があるかどうかが分からない。

import sympy as sp
import numpy as np
import pandas as pd
from scipy import stats
import matplotlib.pyplot as plt
# 等差数列を生成
x = np.linspace(1,-1,61,endpoint = True)
y1 = np.sqrt(1-x**2)
y2 = -1/((1-x**2)**(3/2))
# pdfで確率密度関数を生成
plt.style.use('default')
fig = plt.figure()
# 可視化
plt.plot(x, y1,color="blue", label="y=f(x)=sqrt(1-x^2)")
plt.plot(x, -y1,color="red", label="y=-f(x)=-sqrt(1-x^2)")
plt.plot(x, y2,color="skyblue", label="y=f''(x)=-x/(1-x^2)^(3/2)")
plt.plot(x, -y2,color="orange", label="y=-f''(x)=x/(1-x^2)^(3/2)")
plt.plot(y2, x,color="lightgreen", label="x=f''(y)=-y/(1-y^2)^(3/2)")
plt.plot(-y2, x,color="darkgreen", label="x=-f''(y)=y/(1-y^2)^(3/2)")
plt.ylim([-4,4])
plt.xlim([-4,4])
plt.xlabel("x")
plt.ylabel("y")
plt.title("Circular Function")
ax = fig.add_subplot(111)
ax.set_aspect('equal')
ax.legend(loc='lower right')
plt.show()
曲率と曲率半径
この考え方をさらに発展させたのが曲率(Curvature)$\kappa$の概念となります。
曲率と曲率半径
曲線上の点(a,f(a))においてその点近傍の曲線をもっともよく近似する円の半径Rを想定する。それはその曲線を近似する円の方程式を求める過程で得られる。
その円(曲率円)の方程式は以下となる。
( x - X )^{2} + ( y - Y )^{2} = R^{2}
これをyについて解いたものをF(x)と置く。さしあたってf''(x)=0の場合については考えないものとする。
y = F(x) =
\begin{cases}
Y + \sqrt{ R^{2} - ( x - X )^{2} } &( f''(x) \lt 0 ) \\[3pt]
Y - \sqrt{ R^{2} - ( x - X )^{2} } &( f''(x) \gt 0 )
\end{cases}
- ここで第一に曲率円は問題としている曲線上の点(a,f(a))を通る。
f(a)=F(a)
- 第二にその点で曲率円の接線の傾きがf(a)の接線の傾きに一致している。
f'(a)=F'(a)
- 曲線f(x)を直線で近似する場合にはこの2条件(点と接線の条件)だけで十分だが、今回は円という曲線で近似したいのであり、かつ曲線の曲がり具合はその関数の2階微分によってもっとも大ざっぱに表現されるので第三の条件として「f(a)の2階微分が点(a,f(a))においてf(x)のそれに一致している」という条件を課す。
f''(a)=F''(a)
この連立方程式を解くと以下となり、曲率半径Rが求まる(導出過程は引用元参照の事)。
\begin{align}
X &= x - \frac{\bigl(\,1+f'(x)^{2}\,\bigl)\,f'(x)}{f''(x)} \\
Y &= f(x) + \frac{1+f'(x)^{2}}{f''(x)} \\
&R = \frac{(1+f'(x)^{2})^{3/2}}{|f''(x)|}
\end{align}
実際に作図してみると曲率半径Rが大きいほどその曲線の曲がり具合は小さくなり、逆に曲率半径Rが小さいほどその曲線はその点で大きく曲がる。これより曲率半径Rの逆数$\frac{1}{R}$を曲線の曲がり具合を表す量と見て曲線f(x)の曲率$\kappa$と定義する。
\kappa = \frac{f''(x)}{\bigl(\,1+f'(x)^{\,2}\,\bigr)^{3/2}}
ここでf''(x)にかかる絶対値を外した結果、曲率$\kappa$はf''(x)と同じ符号をもつことになり、曲線が下に凸である点では$\kappa>0$、上に凸である点では$\kappa<0$となる。
-
対象が(半径1の単位円に重なる)円関数$x^2+y^2=1$そのものだった場合は曲率半径Rも曲率$\kappa$も$\mp$1となり、これが出発点となる(上掲のグラフにも見られる通り下凸の半円が曲率$\kappa>0$、上凸の半円が曲率$\kappa<0$に対応する点に注意。この性質は**ベルカーブ関数**$e^{-x^2}$にもしっかり現れている)。
【Pyrhon演算処理】確率密度空間と累積分布空間②中心極限定理の可視化

-
f''(x)=0である点においては$\kappa=0$となる。すなわち直線の曲率や、曲線の変曲点における曲率$\kappa$は0となり、この(曲率半径Rの計算が0除算になる)場合について曲率半径$R=∞$と定義する。
-
$f(x)=\frac{a x^{2}}{2}$の場合は以下。
f(x)=\frac{a x^{2}}{2}\\
f^{\prime}(x)=a x\\
f^{\prime\prime}(x)=a\\
\kappa =\frac{a}{\left(a^{2} x^{2} + 1\right)^{\frac{3}{2}}}
import sympy as sp
a,x= sp.symbols("a,x")
# Rows
f0=sp.Rational(1,2)*a*x**2
f1=sp.diff(f0,x,1)
f2=sp.diff(f0,x,2)
k=f2/((1+f1**2)**sp.Rational(3,2))
# Columns
sp.init_printing()
display(f0)
print("f(x)="+sp.latex(f0))
display(sp.simplify(f1))
print("f^{\prime}(x)="+sp.latex(sp.simplify(f1)))
display(sp.simplify(f2))
print("f^{\prime\prime}(x)="+sp.latex(sp.simplify(f2)))
display(sp.simplify(k))
print("\kappa ="+sp.latex(sp.simplify(k)))
import sympy as sp
import numpy as np
import pandas as pd
from scipy import stats
import matplotlib.pyplot as plt
# 等差数列を生成
x = np.linspace(-5,5,61,endpoint = True)
y1 = (1/2)*x**2
y2 = x
# pdfで確率密度関数を生成
plt.style.use('default')
fig = plt.figure()
# 可視化
plt.hlines(2,-5,5,color="black")
plt.hlines(-2,-5,5,color="black")
plt.vlines(2,-5,5,color="black")
plt.vlines(-2,-5,5,color="black")
plt.plot(x, y1,color="blue", label="y=f(x)=1/2x^2")
plt.plot(x, -y1,color="red", label="y=-f(x)=-1/2x^2")
plt.plot(y1,x,color="skyblue", label="x=f(y)=1/2y^2")
plt.plot(-y1, x,color="orange", label="x=-f(y)=-1/2y^2")
plt.plot(x, y2,color="lightgreen", label="y=f'(x)=x")
plt.plot(x, -y2,color="darkgreen", label="y=-f'(x)=-x")
plt.ylim([-4,4])
plt.xlim([-4,4])
plt.xlabel("x")
plt.ylabel("y")
plt.title("y=1/2x^2/x=1/2y^2 Function")
ax = fig.add_subplot(111)
ax.set_aspect('equal')
ax.legend(loc='lower right')
plt.show()
- $f(x)=- \log{\left(\cos{\left(x \right)} \right)}$の場合は以下。
f(x)=- \log{\left(\cos{\left(x \right)} \right)}\\
f^{\prime}(x)=\tan{\left(x \right)}\\
f^{\prime\prime}(x)=\frac{1}{\cos^{2}{\left(x \right)}}\\
\kappa =\frac{1}{\sqrt{\frac{1}{\cos^{2}{\left(x \right)}}}}=cos(x)
import sympy as sp
a,x= sp.symbols("a,x")
# Rows
f0=-sp.log(sp.cos(x))
f1=sp.diff(f0,x,1)
f2=sp.diff(f0,x,2)
k=f2/((1+f1**2)**sp.Rational(3,2))
# Columns
sp.init_printing()
display(f0)
print("f(x)="+sp.latex(f0))
display(sp.simplify(f1))
print("f^{\prime}(x)="+sp.latex(sp.simplify(f1)))
display(sp.simplify(f2))
print("f^{\prime\prime}(x)="+sp.latex(sp.simplify(f2)))
display(sp.simplify(k))
print("\kappa ="+sp.latex(sp.simplify(k))+"=cos(x)")
import sympy as sp
import numpy as np
import pandas as pd
from scipy import stats
import matplotlib.pyplot as plt
# 等差数列を生成
x = np.linspace(-np.pi/2,np.pi/2,61,endpoint = True)
y1 = -np.log(np.cos(x))
y2 = np.tan(x)
# pdfで確率密度関数を生成
plt.style.use('default')
fig = plt.figure()
# 可視化
plt.plot(x, y1,color="blue", label="y=f(θ)=-log(cos(θ))")
plt.plot(x, -y1,color="red", label="y=-f(θ)=log(cos(θ))")
plt.plot(x, y2,color="skyblue", label="y=f'(θ)=tan(θ)")
plt.plot(x, -y2,color="orange", label="y=-f'(θ)=-tan(θ)")
plt.plot(y2, x,color="lightgreen", label="θ=f'(y)=tan(y)")
plt.plot(-y2, x,color="darkgreen", label="θ=-f'(y)=-tan(y)")
plt.ylim([-4,4])
plt.xlim([-4,4])
plt.xlabel("θ")
plt.ylabel("y")
plt.title("-log(cos(θ)) Function(θ=-π/2→π/2)")
ax = fig.add_subplot(111)
ax.set_aspect('equal')
ax.legend(loc='lower right')
plt.show()
import sympy as sp
import numpy as np
import pandas as pd
from scipy import stats
import matplotlib.pyplot as plt
# 等差数列を生成
x = np.linspace(-np.pi/2,np.pi/2,61,endpoint = True)
x1=np.linspace(-1,1,61,endpoint = True)
y0 =(0+1j)**(2*x)
y1 = -np.log(np.cos(x))
y2 = 1/np.cos(x)**2
# pdfで確率密度関数を生成
plt.style.use('default')
fig = plt.figure()
# 可視化
plt.plot(y0.real, y0.imag,color="black", label="y=exp(θi)")
plt.plot(x, y1,color="blue", label="y=f(θ)=-log(cos(θ))")
plt.plot(x, -y1,color="red", label="y=-f(θ)=log(cos(θ))")
plt.plot(x, y2,color="skyblue", label="y=f''(θ)=1/cos(θ)^2")
plt.plot(x, -y2,color="orange", label="y=-f''(θ)=-cos(θ)^2")
plt.plot(y2, x,color="lightgreen", label="θ=f''(y)=1/cos(y)^2")
plt.plot(-y2, x,color="darkgreen", label="θ=-f''(y)=-1/cos(y)^2")
plt.ylim([-4,4])
plt.xlim([-4,4])
plt.xlabel("θ")
plt.ylabel("y")
plt.title("-log(cos(θ)) Function(θ=-π/2→π/2)")
ax = fig.add_subplot(111)
ax.set_aspect('equal')
ax.legend(loc='lower right')
plt.show()
背景にあるのはこういう考え方です。
曲率と曲率半径 - 物理のかぎしっぽ
読者の多くの方が,微積分の勉強で,曲線の微小部分を接線で近似する,という見方に触れたことがあると思います。曲線を直線で近似とはずいぶん乱暴な話ですが,これは一番簡単な近似で,一次近似とも言うべきものです。
もう少し曲がり具合を表現しようと頑張ってみたのが,曲がり具合を円弧で近似する二次近似です。それでも,一般の複雑な曲線の曲がり具合を表現するには簡単すぎますが,直線よりかは大分ましでしょう.曲率を,曲線の曲がり具合の二次近似だと考えると少し見通しが良くなると思います。
積分の世界において、精度向上を求めて区分求積法(直方体近似)から台形近似に進む感覚と似ていますね。
台形公式を用いた積分の近似とその誤差 | 高校数学の美しい物語
まさしく「解析学は(精度を上げる為には)手段を選ばない」方便の世界…
【初心者向け】「泳ぐ」数理について。
「認識可能範囲外を跋扈する絶対他者」としての「複素平面」の跳梁
ここまで踏み込みながら「複素平面(Complex Plane)」や行列演算との関係について一言も触れない辺りが高校数学独特のいやらしさと申せましょう。
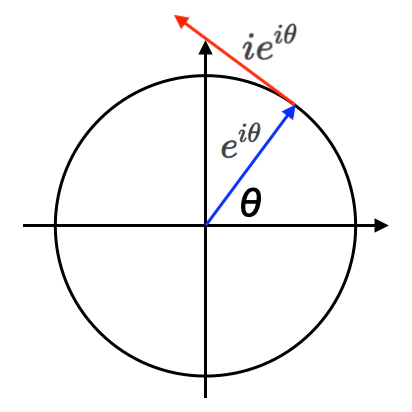
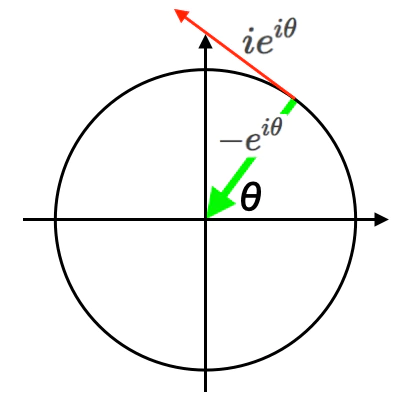
①$m_1m_2=-1$なる概念は、$m_1=m_2$の時に容易に虚数(Imaginal)の定義$i^2=-1$へと拡張し得る。そして交代関数$y=-1^x=i^{2x}$の定義を踏み台にすれば極座標系(r,θ)の世界、すなわちオイラーの公式(Eulerian Formula)$e^{θi}=cos(θ)+sin(θ)i$を群演算とする「複素平面の世界」へと移行出来るのである。
【数理考古学】解析学史に「虚数概念」をもたらした交代級数
②「複素平面の世界」においては二項展開(Binomial Expansion)から三平方の定理$a^2=b^2+c^2$を導出するのも容易となる。
【Python演算処理】パスカルの三角形と二項定理または二項展開
【数理考古学】ピタゴラスの定理あるいは三平方の定理からの出発
- 余弦定理(Cosine Formula)を用いた証明では、まず$a^2=(b-c)^2=b^2+c^2−2bc*\cos(α)$と展開。角度が直角すなわち$\cos(\frac{π}{2})=0$の場合における特殊例として以下が計算されるが、三角関数の登場の仕方に唐突感が否めない。
a^2=b^2+c^2−2bc*0=b^2+c^2
- オイラーの公式(Euler's Formula)あるいは共益複素数(Conjugate Complex Number)同士の打ち消し作用を用いた証明では、これが連続的に以下の様に二項定理の概念に収まったまま計算される展開を迎える。
1=e^0=e^{iθ-iθ}=e^{iθ}-e^{iθ}\\
=(\cos(θ)+\sin(θ)i)(\cos(θ)-\sin(θ)i)\\
=\cos(θ)^2+\sin(θ)i-\sin(θ)i-sin(θ)i^2\\
=cos(θ)^2+sin(θ)^2
③「複素平面の世界」においては一貫して$z=x+iy:x=Re(z),y=Im(z)$なる考え方で座標処理を扱う様になるので「y軸に平行な直線を$y=mx+n$の形で表すことは出来ない」なる制約もなくなる。もちろん円の方程式$x^2+y^2=1$の微分結果たる$\frac{dy}{dx}=−\frac{x}{y} (y≠0)$からもy≠0の条件が消える。
そしてさらには以下の「虚冪の概念」がまとめて導入される展開を迎えるのです。
【Python演算処理】冪算と乗除算の関係について。
- 三角関数の微分(それぞれが+90度の変遷に対応)
\cos(θ)\frac{d^n}{dθ^n}=(-\sin(θ),-\cos(θ),\sin(θ),\cos(θ),…)\\
\sin(θ)\frac{d^n}{dθ^n}=(\cos(θ),-\sin(θ),-\cos(θ),\sin(θ),…)
- 三角関数の積分(それぞれが-90度の変遷に対応)
\int \int \int … \int \cos(θ)(dθ)=(\sin(θ),-\cos(θ),-\sin(θ),\cos(θ),…)\\
\int \int \int … \int \sin(θ)(dθ)=(-\cos(θ),-\sin(θ),\cos(θ),\sin(θ),…)
- 三角関数と指数・対数関数の関係
- $\cos(θ)=\frac{e^{θi}+e^{-θi}}{2}$
- $\sin(θ)=\frac{e^{θi}-e^{-θi}}{2i}$
- $e^{ix}\frac{d^n}{dθ^n}=(i e^{i x}(-\log ix),-e^{ix},-i e^{i x}(\log ix),e^{ix},…)$
- $\int \int \int … \int e^{ix}(dθ)=(- i e^{i x}(\log ix),- e^{i x},i e^{i x}(-\log ix),e^{ix},…)$
これぞまさしく「高校数学と大学数学の間に横たわる深過ぎる海溝」という次第なんですね。人によってこれが「断絶」としか見えず挫折してしまったりします。実際私も数年前に数学再勉強に着手するまではそちら側のグループの一員だったのです(というか、いまだにその一員から抜け出せた実感が伴っていなかったりする)。
行列演算における「群表現論」との関係
ところで指数関数と対数関数の往復にはxy置換、すなわち$y=e^x$を$x=e^y$に置き換える変換が現れますが、これは行列演算における「正方行列の転置」の概念に他ならないのです。
【Python演算処理】冪算と乗除算の関係について。

| 自然指数関数 | 自然対数関数 | |
|---|---|---|
| 0 | y=exp(x) | y=log(x) |
| 1 | y=exp(-x) | y=log(-x) |
| 2 | y=-exp(x) | y=-log(x) |
| 3 | y=-exp(-x) | y=-log(-x) |
以下の行列はそれぞれ転置の結果によって定義される特別例となる。
-
対称行列(Symmetric Matrix):転置が元の行列と等しい (${}^tA=A$)。
対称行列 -Wikipedia -
反対称行列(Antimetric Matrix)/交代行列(Antimetric Matrix):転置が元の行列に −1 をかけたものになる(${}^tA=-A$)
交代行列 -Wikipedia -
直交行列(Orthogonal Matrix):転置が元の行列の逆行列になる(${}^tA=A^{-1}$)
直交行列 -Wikipedia
これらの行列はそれぞれ随伴行列(Adjoint Matrix:行列のエルミート共役)${}^{\dagger}A$に対するエルミート行列(Hermitian Matrix)、歪エルミート行列(Skew-Hermitian Matrix)、ユニタリ行列(Unitary Matrix)に相当する。
随伴行列 -Wikipedia
エルミート行列 -Wikipedia
歪エルミート行列 -Wikipedia
ユニタリ行列 -Wikipedia
ここまでの文面に登場した「対称性/反対称性」「交代性」「直交性」「複素共役」といった諸概念の発展形のリヴァイヴァル。さらにいうと、そもそも群論の世界には「複素平面の世界」において半径1の単位円を規定するオイラーの公式(Eulerian Formula)$e^{θi}=\cos(θ)+\sin(θ)i$そのものを群演算の出発点として共有する群が多数存在したりもするのです。
【Python演算処理】冪算と乗除算の関係について。
- 1次元トーラス、すなわち1次元球面(半径1の単位円)=円周群(Circle Group)𝕋=特殊直交群(Special Orthogonal Group)SO(2)=複素1次ユニタリ群(Unitary Group)U(1)=リー群$S^1$の集合論的定義
\mathbb {T} =SO(2) =U(1) =S^1 =\{z\in \mathbb {C} :|z|=1\}
- 例えばこのうち一次元トーラス$s^1$の直積(Direct Product)を取り続けると二次元トーラス(単位トーラス)$s^2$と三次元トーラス(Quaternion=四元数)$s^3$が連続して現れる。




その一方、行列演算の世界は二次形式から三次形式に発展する過程で二項定理からの逸脱を開始します。どうhやらこの辺りからが大学数学の本格的始まりとなるらしい?
【Python演算処理】行列演算の基本④大源流における記述統計学との密接な関連性?
- 二次形式(ここまでは二項定理の枠内)
(a+b)^2=a^2+2ab+v^2\\
{\left[\begin{matrix}a & b\end{matrix}\right]\left[\begin{matrix}1 & 1\\1 & 1\end{matrix}\right]\left[\begin{matrix}a\\b\end{matrix}\right]=\left[\begin{matrix}\left(a + b\right)^{2}\end{matrix}\right]\\
\left[\begin{matrix}a & b\end{matrix}\right]\left[\begin{matrix}1 & 0\\0 & 0\end{matrix}\right]\left[\begin{matrix}a\\b\end{matrix}\right]=\left[\begin{matrix}a^{2}\end{matrix}\right]\\
\left[\begin{matrix}a & b\end{matrix}\right]\left[\begin{matrix}0 & 1\\0 & 0\end{matrix}\right]\left[\begin{matrix}a\\b\end{matrix}\right]=\left[\begin{matrix}a b\end{matrix}\right]\\
\left[\begin{matrix}a & b\end{matrix}\right]\left[\begin{matrix}0 & 0\\1 & 0\end{matrix}\right]\left[\begin{matrix}a\\b\end{matrix}\right]=\left[\begin{matrix}a b\end{matrix}\right]\\
\left[\begin{matrix}a & b\end{matrix}\right]\left[\begin{matrix}0 & 0\\0 & 1\end{matrix}\right]\left[\begin{matrix}a\\b\end{matrix}\right]=\left[\begin{matrix}b^{2}\end{matrix}\right]
}
- 三次形式(おやおや「パスカルの三角形」からの逸脱?)
(a+b+c)^2=a^2+b^2+c^2+2ab+2bc+2ca\\
\left[\begin{matrix}a & b & c\end{matrix}\right]\left[\begin{matrix}1 & 1 & 1\\1 & 1 & 1\\1 & 1 & 1\end{matrix}\right]\left[\begin{matrix}a\\b\\c\end{matrix}\right]=\left[\begin{matrix}\left(a + b + c\right)^{2}\end{matrix}\right]\\
\left[\begin{matrix}a & b & c\end{matrix}\right]\left[\begin{matrix}1 & 0 & 0\\0 & 0 & 0\\0 & 0 & 0\end{matrix}\right]\left[\begin{matrix}a\\b\\c\end{matrix}\right]=\left[\begin{matrix}a^{2}\end{matrix}\right]\\
\left[\begin{matrix}a & b & c\end{matrix}\right]\left[\begin{matrix}0 & 1 & 0\\0 & 0 & 0\\0 & 0 & 0\end{matrix}\right]\left[\begin{matrix}a\\b\\c\end{matrix}\right]=\left[\begin{matrix}a b\end{matrix}\right]\\
\left[\begin{matrix}a & b & c\end{matrix}\right]\left[\begin{matrix}0 & 0 & 1\\0 & 0 & 0\\0 & 0 & 0\end{matrix}\right]\left[\begin{matrix}a\\b\\c\end{matrix}\right]=\left[\begin{matrix}a c\end{matrix}\right]\\
\left[\begin{matrix}a & b & c\end{matrix}\right]\left[\begin{matrix}0 & 0 & 0\\1 & 0 & 0\\0 & 0 & 0\end{matrix}\right]\left[\begin{matrix}a\\b\\c\end{matrix}\right]=\left[\begin{matrix}a b\end{matrix}\right]\\
\left[\begin{matrix}a & b & c\end{matrix}\right]\left[\begin{matrix}0 & 0 & 0\\0 & 1 & 0\\0 & 0 & 0\end{matrix}\right]\left[\begin{matrix}a\\b\\c\end{matrix}\right]=\left[\begin{matrix}b^{2}\end{matrix}\right]\\
\left[\begin{matrix}a & b & c\end{matrix}\right]\left[\begin{matrix}0 & 0 & 0\\0 & 0 & 1\\0 & 0 & 0\end{matrix}\right]\left[\begin{matrix}a\\b\\c\end{matrix}\right]=\left[\begin{matrix}b c\end{matrix}\right]\\
\left[\begin{matrix}a & b & c\end{matrix}\right]\left[\begin{matrix}0 & 0 & 0\\0 & 0 & 0\\1 & 0 & 0\end{matrix}\right]\left[\begin{matrix}a\\b\\c\end{matrix}\right]=\left[\begin{matrix}a c\end{matrix}\right]\\
\left[\begin{matrix}a & b & c\end{matrix}\right]\left[\begin{matrix}0 & 0 & 0\\0 & 0 & 0\\0 & 1 & 0\end{matrix}\right]\left[\begin{matrix}a\\b\\c\end{matrix}\right]=\left[\begin{matrix}b c\end{matrix}\right]\\
\left[\begin{matrix}a & b & c\end{matrix}\right]\left[\begin{matrix}0 & 0 & 0\\0 & 0 & 0\\0 & 0 & 1\end{matrix}\right]\left[\begin{matrix}a\\b\\c\end{matrix}\right]=\left[\begin{matrix}c^{2}\end{matrix}\right]
import sympy as sp
a,b,c = sp.symbols('a,b,c')
# Rows
x=sp.Matrix([[a,b,c]])
# Columns
y=sp.Matrix([[a],[b],[c]])
a00=sp.Matrix([[1,1,1],[1,1,1],[1,1,1]])
a11=sp.Matrix([[1,0,0],[0,0,0],[0,0,0]])
a12=sp.Matrix([[0,1,0],[0,0,0],[0,0,0]])
a13=sp.Matrix([[0,0,1],[0,0,0],[0,0,0]])
a21=sp.Matrix([[0,0,0],[1,0,0],[0,0,0]])
a22=sp.Matrix([[0,0,0],[0,1,0],[0,0,0]])
a23=sp.Matrix([[0,0,0],[0,0,1],[0,0,0]])
a31=sp.Matrix([[0,0,0],[0,0,0],[1,0,0]])
a32=sp.Matrix([[0,0,0],[0,0,0],[0,1,0]])
a33=sp.Matrix([[0,0,0],[0,0,0],[0,0,1]])
sp.init_printing()
display(x)
display(a00)
display(a11)
display(a12)
display(a13)
display(a21)
display(a22)
display(a23)
display(a31)
display(a32)
display(a33)
display(y)
display(sp.simplify(x*a00*y))
print(sp.latex(x)+sp.latex(a00)+sp.latex(y)+"="+sp.latex(sp.simplify(x*a00*y)))
display(sp.simplify(x*a11*y))
print(sp.latex(x)+sp.latex(a11)+sp.latex(y)+"="+sp.latex(sp.simplify(x*a11*y)))
display(sp.simplify(x*a12*y))
print(sp.latex(x)+sp.latex(a12)+sp.latex(y)+"="+sp.latex(sp.simplify(x*a12*y)))
display(sp.simplify(x*a13*y))
print(sp.latex(x)+sp.latex(a13)+sp.latex(y)+"="+sp.latex(sp.simplify(x*a13*y)))
display(sp.simplify(x*a21*y))
print(sp.latex(x)+sp.latex(a21)+sp.latex(y)+"="+sp.latex(sp.simplify(x*a21*y)))
display(sp.simplify(x*a22*y))
print(sp.latex(x)+sp.latex(a22)+sp.latex(y)+"="+sp.latex(sp.simplify(x*a22*y)))
display(sp.simplify(x*a23*y))
print(sp.latex(x)+sp.latex(a23)+sp.latex(y)+"="+sp.latex(sp.simplify(x*a23*y)))
display(sp.simplify(x*a31*y))
print(sp.latex(x)+sp.latex(a31)+sp.latex(y)+"="+sp.latex(sp.simplify(x*a31*y)))
display(sp.simplify(x*a32*y))
print(sp.latex(x)+sp.latex(a32)+sp.latex(y)+"="+sp.latex(sp.simplify(x*a32*y)))
display(sp.simplify(x*a33*y))
print(sp.latex(x)+sp.latex(a33)+sp.latex(y)+"="+sp.latex(sp.simplify(x*a33*y)))
そんな感じで以下続報…