<科目> 機械学習 第七章:サポートベクターマシン

#<科目> 機械学習

目次
第一章:線形回帰モデル
[第二章:非線形回帰モデル]
(https://qiita.com/matsukura04583/items/baa3f2269537036abc57)
[第三章:ロジスティク回帰モデル]
(https://qiita.com/matsukura04583/items/0fb73183e4a7a6f06aa5)
[第四章:主成分分析]
(https://qiita.com/matsukura04583/items/b3b5d2d22189afc9c81c)
[第五章:アルゴリズム1(k近傍法(kNN))]
(https://qiita.com/matsukura04583/items/543719b44159322221ed)
[第六章:アルゴリズム2(k-means)]
(https://qiita.com/matsukura04583/items/050c98c7bb1c9e91be71)
[第七章:サポートベクターマシン]
(https://qiita.com/matsukura04583/items/6b718642bcbf97ae2ca8)

##第七章:サポートベクターマシン

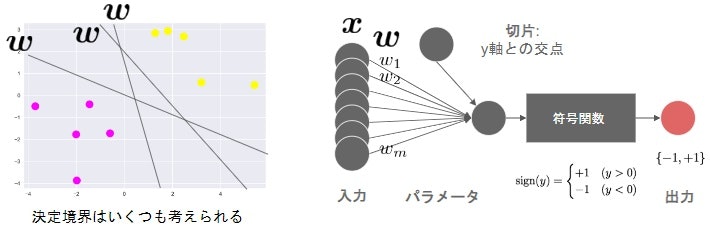
• 2クラス分類のための機械学習手法
• 線形モデルの正負で2値分類

y=w^Tx+b=\sum_{j=1}^{m} w_jx_j+b

• 線形判別関数ともっとも近いデータ点との距離をマージンという

• マージンが最大となる線形判別関数を求める
  

• マージンはパラメータに依存する。
  SVMの決定関数

y(x)=w^Tx+b=\sum_{j=1}^{m} a_it_ix~Tx+b

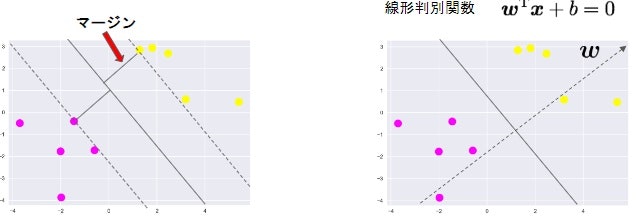
• サポートベクター

  • 分離超平面を構成する学習データは、サポートベクターだけで残りのデータは不要
    

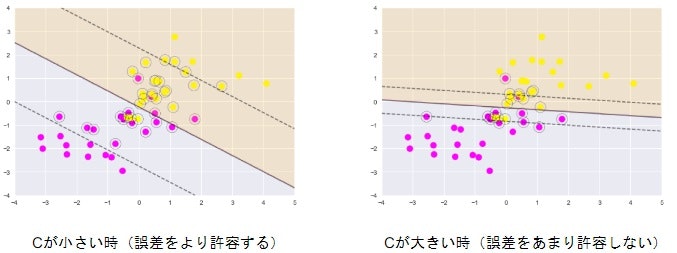
• ソフトマージンSVM

  • サンプルを線形分離できないとき
  • 誤差を許容し、誤差に対してペナルティを与える
  • 線形分離できない場合でも対応
  • パラメータCの大小で決定境界が変化

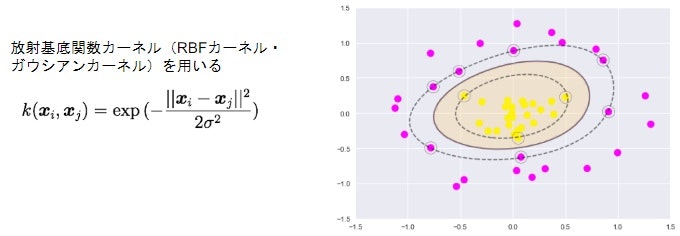
• カーネルトリック

  • カーネル関数$$k(x_ix_j)=\phi(x_i)^T\phi(x_j)$$
  • 高次元ベクトルの内積をスカラー関数で表現
  • 特徴空間が高次元でも計算コストを抑えられる

• 非線形カーネルを用いた分離

  • 非線形な分離が可能
    

• ラグランジュの未定乗数法

  • 定義
    

(参考)ラグランジュの未定乗数法でサポートベクターマシンの主問題を解く

###(演習1)SVMによるアヤメの分類
サポートベクトルマシンについては、以前行った「RaspberryPiではじめる機械学習」で学んだ内容が分かりやすかったので、それを備忘も含めて記載します。

#最初に必要なモジュールをいろいろインポート
from sklearn import datasets, svm
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.colors import ListedColormap

# アヤメのデータをロードし、変数irisに格納する
iris = datasets.load_iris()

# 特徴量のセットを変数Xに、ターゲットを変数yに格納する
X = iris.data
y = iris.target

# Xとyの内容表示
print(X)
print(y)

結果

[[5.1 3.5 1.4 0.2]
 [4.9 3.  1.4 0.2]
 [4.7 3.2 1.3 0.2]
 [4.6 3.1 1.5 0.2]
 [5.  3.6 1.4 0.2]
 [5.4 3.9 1.7 0.4]
 [4.6 3.4 1.4 0.3]
 [5.  3.4 1.5 0.2]
 [4.4 2.9 1.4 0.2]
 [4.9 3.1 1.5 0.1]
 [5.4 3.7 1.5 0.2]
 [4.8 3.4 1.6 0.2]
 [4.8 3.  1.4 0.1]
 [4.3 3.  1.1 0.1]
 [5.8 4.  1.2 0.2]
 [5.7 4.4 1.5 0.4]
 [5.4 3.9 1.3 0.4]
 [5.1 3.5 1.4 0.3]
 [5.7 3.8 1.7 0.3]
 [5.1 3.8 1.5 0.3]
 [5.4 3.4 1.7 0.2]
 [5.1 3.7 1.5 0.4]
 [4.6 3.6 1.  0.2]
 [5.1 3.3 1.7 0.5]
 [4.8 3.4 1.9 0.2]
 [5.  3.  1.6 0.2]
 [5.  3.4 1.6 0.4]
 [5.2 3.5 1.5 0.2]
 [5.2 3.4 1.4 0.2]
 [4.7 3.2 1.6 0.2]
 [4.8 3.1 1.6 0.2]
 [5.4 3.4 1.5 0.4]
 [5.2 4.1 1.5 0.1]
 [5.5 4.2 1.4 0.2]
 [4.9 3.1 1.5 0.2]
 [5.  3.2 1.2 0.2]
 [5.5 3.5 1.3 0.2]
 [4.9 3.6 1.4 0.1]
 [4.4 3.  1.3 0.2]
 [5.1 3.4 1.5 0.2]
 [5.  3.5 1.3 0.3]
 [4.5 2.3 1.3 0.3]
 [4.4 3.2 1.3 0.2]
 [5.  3.5 1.6 0.6]
 [5.1 3.8 1.9 0.4]
 [4.8 3.  1.4 0.3]
 [5.1 3.8 1.6 0.2]
 [4.6 3.2 1.4 0.2]
 [5.3 3.7 1.5 0.2]
 [5.  3.3 1.4 0.2]
 [7.  3.2 4.7 1.4]
 [6.4 3.2 4.5 1.5]
 [6.9 3.1 4.9 1.5]
 [5.5 2.3 4.  1.3]
 [6.5 2.8 4.6 1.5]
 [5.7 2.8 4.5 1.3]
 [6.3 3.3 4.7 1.6]
 [4.9 2.4 3.3 1. ]
 [6.6 2.9 4.6 1.3]
 [5.2 2.7 3.9 1.4]
 [5.  2.  3.5 1. ]
 [5.9 3.  4.2 1.5]
 [6.  2.2 4.  1. ]
 [6.1 2.9 4.7 1.4]
 [5.6 2.9 3.6 1.3]
 [6.7 3.1 4.4 1.4]
 [5.6 3.  4.5 1.5]
 [5.8 2.7 4.1 1. ]
 [6.2 2.2 4.5 1.5]
 [5.6 2.5 3.9 1.1]
 [5.9 3.2 4.8 1.8]
 [6.1 2.8 4.  1.3]
 [6.3 2.5 4.9 1.5]
 [6.1 2.8 4.7 1.2]
 [6.4 2.9 4.3 1.3]
 [6.6 3.  4.4 1.4]
 [6.8 2.8 4.8 1.4]
 [6.7 3.  5.  1.7]
 [6.  2.9 4.5 1.5]
 [5.7 2.6 3.5 1. ]
 [5.5 2.4 3.8 1.1]
 [5.5 2.4 3.7 1. ]
 [5.8 2.7 3.9 1.2]
 [6.  2.7 5.1 1.6]
 [5.4 3.  4.5 1.5]
 [6.  3.4 4.5 1.6]
 [6.7 3.1 4.7 1.5]
 [6.3 2.3 4.4 1.3]
 [5.6 3.  4.1 1.3]
 [5.5 2.5 4.  1.3]
 [5.5 2.6 4.4 1.2]
 [6.1 3.  4.6 1.4]
 [5.8 2.6 4.  1.2]
 [5.  2.3 3.3 1. ]
 [5.6 2.7 4.2 1.3]
 [5.7 3.  4.2 1.2]
 [5.7 2.9 4.2 1.3]
 [6.2 2.9 4.3 1.3]
 [5.1 2.5 3.  1.1]
 [5.7 2.8 4.1 1.3]
 [6.3 3.3 6.  2.5]
 [5.8 2.7 5.1 1.9]
 [7.1 3.  5.9 2.1]
 [6.3 2.9 5.6 1.8]
 [6.5 3.  5.8 2.2]
 [7.6 3.  6.6 2.1]
 [4.9 2.5 4.5 1.7]
 [7.3 2.9 6.3 1.8]
 [6.7 2.5 5.8 1.8]
 [7.2 3.6 6.1 2.5]
 [6.5 3.2 5.1 2. ]
 [6.4 2.7 5.3 1.9]
 [6.8 3.  5.5 2.1]
 [5.7 2.5 5.  2. ]
 [5.8 2.8 5.1 2.4]
 [6.4 3.2 5.3 2.3]
 [6.5 3.  5.5 1.8]
 [7.7 3.8 6.7 2.2]
 [7.7 2.6 6.9 2.3]
 [6.  2.2 5.  1.5]
 [6.9 3.2 5.7 2.3]
 [5.6 2.8 4.9 2. ]
 [7.7 2.8 6.7 2. ]
 [6.3 2.7 4.9 1.8]
 [6.7 3.3 5.7 2.1]
 [7.2 3.2 6.  1.8]
 [6.2 2.8 4.8 1.8]
 [6.1 3.  4.9 1.8]
 [6.4 2.8 5.6 2.1]
 [7.2 3.  5.8 1.6]
 [7.4 2.8 6.1 1.9]
 [7.9 3.8 6.4 2. ]
 [6.4 2.8 5.6 2.2]
 [6.3 2.8 5.1 1.5]
 [6.1 2.6 5.6 1.4]
 [7.7 3.  6.1 2.3]
 [6.3 3.4 5.6 2.4]
 [6.4 3.1 5.5 1.8]
 [6.  3.  4.8 1.8]
 [6.9 3.1 5.4 2.1]
 [6.7 3.1 5.6 2.4]
 [6.9 3.1 5.1 2.3]
 [5.8 2.7 5.1 1.9]
 [6.8 3.2 5.9 2.3]
 [6.7 3.3 5.7 2.5]
 [6.7 3.  5.2 2.3]
 [6.3 2.5 5.  1.9]
 [6.5 3.  5.2 2. ]
 [6.2 3.4 5.4 2.3]
 [5.9 3.  5.1 1.8]]
[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2
 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
 2 2]

データのサンプル数150, 特徴量の次元4であることが確認できます。
yは、分類のTargetの判定結果を持っている。こちらも150個。

print(X.shape)
print(y.shape)

結果

(150, 4)
(150,)

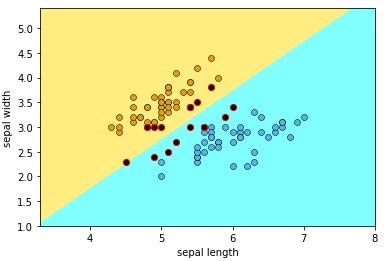
####線形サポートベクトルマシンによる2特徴量・2クラスの分類(1)
ターゲットはiris virginica(2) でない 、2種類 iris setosa (0) と iris versicolor (1) のみを対象として分類します。

# 特徴量を外花被片の長さ(sepal length)と幅(sepal width)の
# 2つのみに制限(2次元で考えるため)
X = X[:,:2]

# ターゲットは2 (iris virginica) でない 、2種類 iris setosa (0) と iris versicolor (1) 
# のみを対象とする (領域の2分割)
X = X[Target!=2]
Target = Target[Target!=2]

# 分類用にサポートベクトルマシン (Support Vector Classifier) を用意
clf = svm.SVC(C=1.0, kernel='linear')
# データに最適化フィット
clf.fit(X, Target)

##### 分類結果を背景の色分けにより表示

# 外花被片の長さ(sepal length)と幅(sepal width)の最小値
# と最大値からそれぞれ1ずつ広げた領域をグラフ表示エリアとする
#　表示のコツのようなもの
x_min = min(X[:,0]) - 1
x_max = max(X[:,0]) + 1
Target_min = min(X[:,1]) - 1
Target_max = max(X[:,1]) + 1

# グラフ表示エリアを縦横500ずつのグリッドに区切る
# (分類クラスに応じて背景に色を塗るため)
XX, YY = np.mgrid[x_min:x_max:500j, Target_min:Target_max:500j]

# グリッドの点をscikit-learn用の入力に並べなおす
Xg = np.c_[XX.ravel(), YY.ravel()]

# 各グリッドの点が属するクラス(0か1)の予測をZに格納
Z = clf.predict(Xg)

# Zをグリッド上に並べなおす
Z = Z.reshape(XX.shape)

# クラス0 (iris setosa) が薄オレンジ (1, 0.93, 0.5, 1)
# クラス1 (iris versicolor) が薄青 (0.5, 1, 1, 1)
cmap01 = ListedColormap([(0.5, 1, 1, 1), (1, 0.93, 0.5, 1)])

# 背景の色を表示
plt.pcolormesh(XX, YY, Z==0, cmap=cmap01)

# 軸ラベルを設定
plt.xlabel('sepal length')
plt.ylabel('sepal width')

##### ターゲットに応じた色付きでデータ点を表示

# iris setosa (Target=0) のデータのみを取り出す
Xc0 = X[Target==0]
# iris versicolor (Target=1) のデータのみを取り出す
Xc1 = X[Target==1]

# iris setosa のデータXc0をプロット
plt.scatter(Xc0[:,0], Xc0[:,1], c='#E69F00', linewidths=0.5, edgecolors='black')
# iris versicolor のデータXc1をプロット
plt.scatter(Xc1[:,0], Xc1[:,1], c='#56B4E9', linewidths=0.5, edgecolors='black')

# サポートベクトルを取得
SV = clf.support_vectors_

# サポートベクトルを可視化
# plt.scatter(SV[:, 0], SV[:, 1],
#                    s=100, facecolors='none', edgecolors='k')

# サポートベクトルの点に対し、赤い枠線を表示
#plt.scatter(SV[:,0], SV[:,1], c=(0,0,0,0), linewidths=1.0, edgecolors='red')
plt.scatter(SV[:,0], SV[:,1], c='black', linewidths=1.0, edgecolors='red')

# 描画したグラフを表示
plt.show()

####線形サポートベクトルマシンによる2特徴量・2クラスの分類(2)
ターゲットは2 iris setosa (0)でない 、2種類 (iris virginica) と iris versicolor (1) のみを対象として分類します。

# 次をやるために再ロードしてセットします。
# アヤメのデータをロードし、変数irisに格納。
iris = datasets.load_iris()

# 特徴量のセットを変数Xに、ターゲットを変数yに格納
X = iris.data
y = iris.target

# 特徴量を外花被片の長さ(sepal length)と幅(sepal width)の
# 2つのみに制限(2次元で考えるため)
X = X[:,:2]

# ターゲットは0 (iris setosa) でないもの, 
# つまり iris versicolor (1) と iris virginica (2) のみを対象とする
# (領域の2分割)
X = X[y!=0]
y = y[y!=0]

# 分類用にサポートベクトルマシンを用意
clf = svm.SVC(C=1.0, kernel='linear')
# データに最適化
clf.fit(X, y)

##### 分類結果を背景の色分けにより表示

# 外花被片の長さ(sepal length)と幅(sepal width)の
# 最小値と最大値からそれぞれ1ずつ広げた領域を
# グラフ表示エリアとする
x_min = min(X[:,0]) - 1
x_max = max(X[:,0]) + 1
y_min = min(X[:,1]) - 1
y_max = max(X[:,1]) + 1

# グラフ表示エリアを縦横500ずつのグリッドに区切る
# (分類クラスに応じて背景に色を塗るため)
XX, YY = np.mgrid[x_min:x_max:500j, y_min:y_max:500j]

# グリッドの点をscikit-learn用の入力に並べなおす
Xg = np.c_[XX.ravel(), YY.ravel()]

# 各グリッドの点が属するクラス(1か2)の予測をZに格納
Z = clf.predict(Xg)

# グリッド上に並べなおす
Z = Z.reshape(XX.shape)

#　種類に応じて背景の色を変えている
# クラス1 (iris versicolor) が薄青 (0.5, 1, 1, 1)
# クラス2 (iris setosa) が薄緑 (0.5, 0.75, 0.5, 1)
cmap12 = ListedColormap([(0.5, 0.75, 0.5, 1), (0.5, 1, 1, 1)])

# 背景の色を表示を薄青・薄緑の2色のキャンパスに変更する
plt.pcolormesh(XX, YY, Z==1, cmap=cmap12)

# 軸ラベルを設定　残念ながら日本語は使えない
plt.xlabel('sepal length')
plt.ylabel('sepal width')

##### ターゲットに応じた色付きでデータ点を表示

# iris versicolor (y=1) のデータのみを取り出す
Xc1 = X[y==1]
# iris virginica (y=2) のデータのみを取り出す
Xc2 = X[y==2]

# iris versicolor のデータXc1をプロット
plt.scatter(Xc1[:,0], Xc1[:,1], c='#56B4E9',linewidth=0.5, edgecolors='black')
# iris virginica のデータXc2をプロット
plt.scatter(Xc2[:,0], Xc2[:,1], c='#008000',linewidth=0.5, edgecolors='black')

# サポートベクトルの取得
SV = clf.support_vectors_
# サポートベクトルの点に対し、赤い枠線を表示
plt.scatter(SV[:,0], SV[:,1], c='black', linewidths=1.0, edgecolors='red')

# 描画したグラフを表示
plt.show()

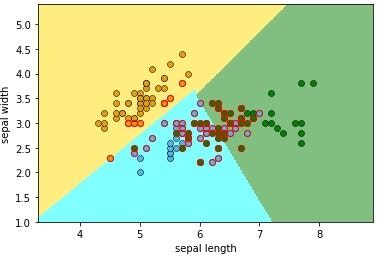
####線形サポートベクトルマシンによる2特徴量・3クラスの分類
特徴量はそのままで、クラスを1つ増やして3つにしてみます。iris setosa (0)、iris versicolor (1) 、iris virginica(2)の3つを対象として分類します。
scikit-learnのデフォルトでは、1対他方式(one-vs-the-rest,ovr)で分類します。

# アヤメのデータをロードし、変数irisに格納
iris = datasets.load_iris()

# 特徴量のセットを変数Xに、ターゲットを変数yに格納
X = iris.data
y = iris.target

# 特徴量を外花被片の長さ(sepal length)と幅(sepal width)の
# 2つのみに制限(2次元で考えるため)
X = X[:,:2]

# 分類用にサポートベクトルマシンを用意
clf = svm.SVC(C=1.0, kernel='linear', decision_function_shape='ovr')
# 'auto'を指定すると1/(次元)がセットされる。この場合、1/2=0.5
#clf = svm.SVC(C=1.0, kernel='rbf', gamma='auto', decision_function_shape='ovr')
# gammaを大きくすると、曲率が大きい（よく曲がる）境界となる
#clf = svm.SVC(C=1.0, kernel='rbf', gamma=1.0, decision_function_shape='ovr')
# データに最適化
clf.fit(X, y)

##### 分類結果を背景の色分けにより表示

# 外花被片の長さ(sepal length)と幅(sepal width)の
# 最小値と最大値からそれぞれ1ずつ広げた領域を
# グラフ表示エリアとする
x_min = min(X[:,0]) - 1
x_max = max(X[:,0]) + 1
y_min = min(X[:,1]) - 1
y_max = max(X[:,1]) + 1

# グラフ表示エリアを縦横500ずつのグリッドに区切る
# (分類クラスに応じて背景に色を塗るため)
XX, YY = np.mgrid[x_min:x_max:500j, y_min:y_max:500j]

# グリッドの点をscikit-learn用の入力に並べなおす
Xg = np.c_[XX.ravel(), YY.ravel()]

# 各グリッドの点が属するクラス(0～2)の予測をZに格納
Z = clf.predict(Xg)

# グリッド上に並べなおす
Z = Z.reshape(XX.shape)

# クラス0 (iris setosa) が薄オレンジ (1, 0.93, 0.5, 1)
# クラス1 (iris versicolor) が薄青 (0.5, 1, 1, 1)
# クラス2 (iris virginica) が薄緑 (0.5, 0.75, 0.5, 1)
cmap0 = ListedColormap([(0, 0, 0, 0), (1, 0.93, 0.5, 1)])
cmap1 = ListedColormap([(0, 0, 0, 0), (0.5, 1, 1, 1)])
cmap2 = ListedColormap([(0, 0, 0, 0), (0.5, 0.75, 0.5, 1)])

# 背景の色を表示
plt.pcolormesh(XX, YY, Z==0, cmap=cmap0)
plt.pcolormesh(XX, YY, Z==1, cmap=cmap1)
plt.pcolormesh(XX, YY, Z==2, cmap=cmap2)

# 軸ラベルを設定
plt.xlabel('sepal length')
plt.ylabel('sepal width')

##### ターゲットに応じた色付きでデータ点を表示

# iris setosa (y=0) のデータのみを取り出す
Xc0 = X[y==0]
# iris versicolor (y=1) のデータのみを取り出す
Xc1 = X[y==1]
# iris virginica (y=2) のデータのみを取り出す
Xc2 = X[y==2]

# iris setosa のデータXc0をプロット
plt.scatter(Xc0[:,0], Xc0[:,1], c='#E69F00', linewidths=0.5, edgecolors='black')
# iris versicolor のデータXc1をプロット
plt.scatter(Xc1[:,0], Xc1[:,1], c='#56B4E9', linewidths=0.5, edgecolors='black')
# iris virginica のデータXc2をプロット
plt.scatter(Xc2[:,0], Xc2[:,1], c='#008000', linewidths=0.5, edgecolors='black')

# サポートベクトルを取得
SV = clf.support_vectors_
# サポートベクトルの点に対し、赤い枠線を表示
plt.scatter(SV[:,0], SV[:,1], c=(0,0,0,0), linewidths=1.0, edgecolors='red')
#plt.scatter(SV[:,0], SV[:,1], c='black', linewidths=1.0, edgecolors='red')

# 描画したグラフを表示
plt.show()

(参考)[plt.scatter散布図の色の使い方] (https://pythondatascience.plavox.info/matplotlib/%E6%95%A3%E5%B8%83%E5%9B%B3)
ちょっと警告がでますが、赤丸の透過の仕方はまた後日調べます。

関連サイト

第一章:線形回帰モデル
[第二章:非線形回帰モデル]
(https://qiita.com/matsukura04583/items/baa3f2269537036abc57)
[第三章:ロジスティク回帰モデル]
(https://qiita.com/matsukura04583/items/0fb73183e4a7a6f06aa5)
[第四章:主成分分析]
(https://qiita.com/matsukura04583/items/b3b5d2d22189afc9c81c)
[第五章:アルゴリズム1(k近傍法(kNN))]
(https://qiita.com/matsukura04583/items/543719b44159322221ed)
[第六章:アルゴリズム2(k-means)]
(https://qiita.com/matsukura04583/items/050c98c7bb1c9e91be71)
[第七章:サポートベクターマシン]
(https://qiita.com/matsukura04583/items/6b718642bcbf97ae2ca8)