Go to Qiita Advent Calendar 2024 Top
LoginSignup
0
0

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?

@gomi-kuzu

『モデルベース深層学習と深層展開』読み会レポート#11

Posted at

$\def\bm{\boldsymbol}$

概要

  • オンラインで開催している『モデルベース深層学習と深層展開』読み会で得られた知見や気づきをメモしていく
  • ついでに、中身の理解がてらJuliaサンプルコードをPythonに書き直したコードを晒していく
    • 自動微分ライブラリにはJAXを使用する

第11回

大まかな内容

  • ニューラル微分方程式を深層展開で学習
  • 変分問題を解くのに深層展開を活用する方法
  • 変分問題のいち応用先の最適制御問題に深層展開を使う方法
  • 確率微分方程式の中のパラメータを深層展開で獲得する方法

議論になったこと

6.2.2節 あたり

  • ”ユニバーサル性”ってのはニューラルネットの万能近似性を指してる？
    • ->たぶんそう
  • サンプルプログラム眺めながら
    • $\bm{x}$は何故わざわざ２次元にした上で１つ目の変数しか使ってない？
      • １次元だとNNの表現力が落ちるから？
      • 速度の変数項を入れればより精度の良い近似ができるから、その拡張を示唆したもの？
        • ただし、ここでは学習データが位置のみなので、速度の役割はもってないはず

6.3.1節 あたり

  • 完備な数列ってなんだっけ
    • ->コーシー列が常に収束すること。参考
  • 式(6.26)らへん
    • $g_i$は基底ではないか
    • おそらく明示されてないが$g_i(t)$
    • $t_1$~$t_2$の区間は無限に分割できるので、$y(t)$は無限の関数の集合で表現されるが、境界条件を満たすものは全体の無限集合の部分無限集合になってる。それが$\{g_i\}$
      • ただ、計算機で扱うためには有限にしないといけないので適当な$m$で打ち切って$\hat{f}$を作ってる

6.3.3節 あたり

  • DU-RRのサンプルプログラムを眺めながら
    • 全ての時刻に渡って最適化される気持ちはどのへんに入ってる？
      • ->Integrate()関数のfor i in 1:Nの中が$0<t<1$の間の積分、最後に足しているのが始点と終点２つの境界条件に関するペナルティ
        • なので全体としてreturn値が式（６．３２）に対応しており、この勾配を誤差逆伝搬で下る事で$\nabla G=\bm{0}$にたどり着ける
          • その時の重みを使って作られる近似関数は元の変分問題の解$y(t)$の近似になっている
  • DU-RR-randのサンプルプログラム眺めながら
    • 結局学習によって何を獲得している？
    • たくさんサンプリングされる$r$に対応する軌道の平均に近づくような軌跡の関数を獲得する？

6.3.6節 あたり

  • x(1)の境界条件は定めないとあるが、それで変分問題が解けるのか？
    • ->求めたいのは停留値ではなく最小値だから、変分問題自体はとけなくてよい？？
    • ->（６．５６）式の最小化をする時点で、$x(1)=0$と定めたのとほぼ同等では？

6.4.2節 あたり

  • DU-EM法のサンプルプログラムは５章のときに扱ったDU-stabilize-SDE
    • 今回の（6.60）式の関数$a(\cdot)$にあたる部分は５章では線形の式だった。
    • この例で0じゃなく1に収束してる理由は地味にわからん

個人的な気づきなど

  • DU-RR法の全体像が掴みきれてなかったが、議論の中で理解を深めることができた。ただし、変分問題の問題アンサンブルの例の問題設定の方は微妙に理解できてないので、もう少し考えたい。

プログラムでの理解

  • 今回の範囲では、ニューラル微分方程式を深層展開を利用して学習する方法を扱った
  • 和田山先生公開のサンプルプログラムをPythonで再現する
  • プログラムの全文はこの辺に上げている

問題設定

  • 以下の常微分方程式を獲得したい
    • $\frac{d}{dt}\bm{x}(t)= h(\bm{x}(t),t)$
  • $h(\cdot)$をニューラルネットで近似し$h_{\bm{\theta}}(\cdot)$とする
  • 与えられたデータセット$\mathcal{D}\equiv\{ (t^{(k_1)}, \bm{x}^{(k_1)}),(t^{(k_2)}, \bm{x}^{(k_2)}), \cdots ,(t^{(k_K)}, \bm{x}^{(k_K)}) \}$を使ってパラメタ$\bm{\theta}$を学習する
  • $0\leq t \leq T$を$N$分割し、常微分方程式をオイラー近似すると以下の反復式になる
    • $\bm{x}^{(k+1)} = \bm{x}^{(k)}+\eta h_{\bm{\theta}}(\bm{x}^{(k)}, t^{(k)})$
      • $\eta$は刻み幅で$\eta= T/N$
    • $\bm{x}^{(0)} = \bm{x}_0$
      • $\bm{x}_0$は初期値
  • 深層展開では、上記の反復式を経る過程の$\bm{x}$の自乗誤差を計算し、誤差逆伝搬法でニューラルネットの重みを学習する
    • 以下のプログラムではニューラルネットは単純な三層パーセプトロンである

Pythonで実装

必要ライブラリインポート

import numpy as np
import jax
import jax.numpy as jnp

import pandas as pd
import matplotlib.pyplot as plt

import optax
from tqdm.notebook import trange
from functools import partial
from flax import linen as nn
from flax.experimental import nnx
from flax.training import train_state
from typing import Sequence, Callable, Tuple
  • 今回は、最適化ライブラリとしてoptaxを使ってみる

定数の設定

T = 4.0
N = 200
eta = T/N
std = 0.1
train_itr = 500
m = 16
init_std = 1e-3
adam_lr = 1e-2

データセットの生成関数の定義

def gen_dataset(std, func):
    x_data = jnp.zeros(N)
    for i in range(N):
        if i % 10 == 0:
            x_data = x_data.at[i].set(func(eta*i) + std*jnp.array(np.random.randn()))
        else:
            x_data = x_data.at[i].set(jnp.nan)
    return x_data
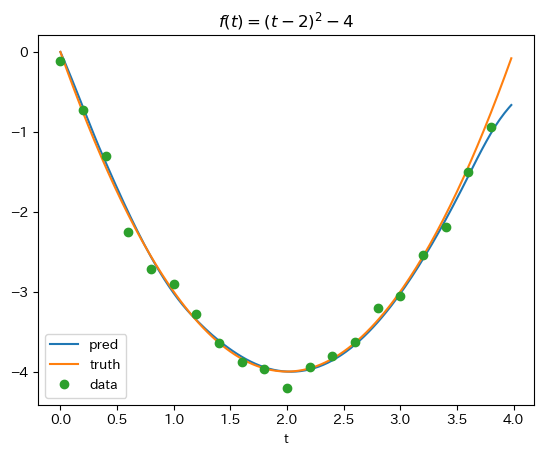
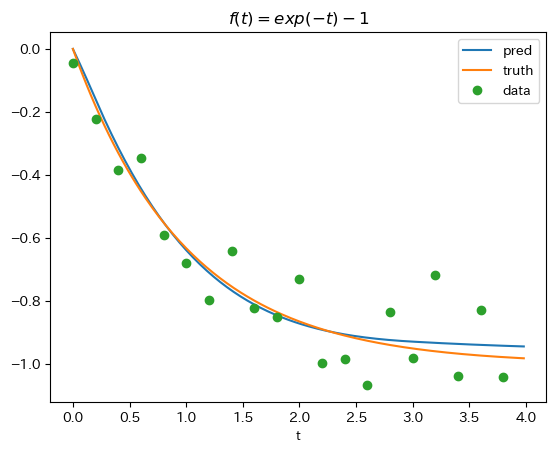
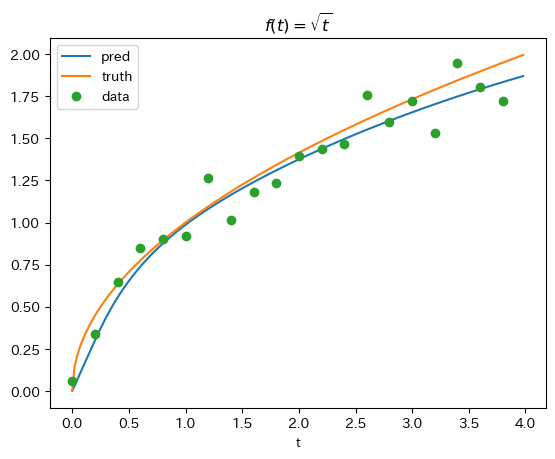
  • この関数を使って、下記の4種類の関数にガウス雑音を加えることでデータ点を生成する
    $$
    y = \sin(t),~~
    y = (t-2)^2-4,~~
    y = \exp(-t)-1,~~
    y = t^{1/2}
    $$

ニューラルネットの定義

class MLP(nn.Module):
    hidden_dim : int
    output_dim : int
    act_fn : Callable = nnx.relu
    
    @nn.compact
    def __call__(self, x):
        x = nn.Dense(self.hidden_dim)(x)
        x = self.act_fn(x)
        x = nn.Dense(self.output_dim)(x)
        return x

mlp = MLP(hidden_dim=m, output_dim=2)
key = jax.random.PRNGKey(0) 
params = mlp.init(key, x = jnp.zeros(2))["params"]
  • かなりオーソドックスな三層パーセプトロン
    • 活性化関数はReLU

オイラー法とDU-Euler法の関数定義

def Euler(max_itr, params):
    x = jnp.zeros(2)
    for i in range(max_itr):
        x += eta*mlp.apply({"params":params}, x)
    return x[0]

@jax.jit
def DU_Euler(x_data, params):
    x = jnp.zeros(2)
    loss = 0.
    for i in range(N):
        x += eta*mlp.apply({"params":params}, x)
        if i % 10 == 0:
            loss += (x[0] - x_data[i])**2
    return loss
  • DU_Euler関数では、10stepに１回データセットとの自乗誤差を計算する
    • それらを足し合わせて誤差関数として出力する

学習関数の定義

tx = optax.adam(learning_rate=adam_lr)
state = train_state.TrainState.create(apply_fn=mlp.apply, params=params, tx=tx)

def step(x_data, state):
    value, grads = jax.value_and_grad(DU_Euler, argnums=-1)(x_data, state.params)
    new_state = state.apply_gradients(grads=grads)
    return value, new_state

def train(x_data, state):
    for itr in trange(train_itr, leave=False):
        value, state = step(x_data, state)
        print("\r"+"\rloss:{}".format(value), end=" ")
    return state
  • optaxではTrainStateという構造体に学習対象や最適化アルゴなどを詰め込んでおいて、学習を管理する。
    • TrainStateの実体（以下：state）はapply_gradients()メソッドの引数に勾配を与えることで、勾配降下したstateを出力できる。
      • 出力されたstate内には更新されたパラメタなどが、メンバとして保持されている

学習と評価

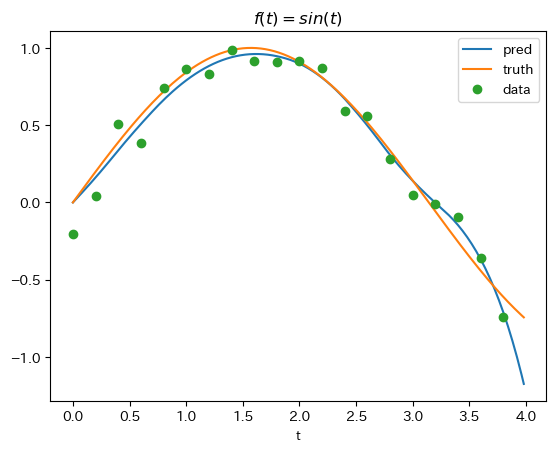
x_data = gen_dataset(std, jnp.sin)
trained_state = train(x_data, state)

df = pd.DataFrame()
df["t"] = jnp.arange(0, T, eta)
df["pred"] = [float(Euler(i, trained_state.params)) for i in range(N)]
df["truth"] = jnp.sin(df["t"].to_numpy())
df["data"] = x_data
fig, ax = plt.subplots()
df.plot(x = "t", y = df.columns[1:3], ax = ax)
df.plot(x = "t", y = "data", marker= "o", linestyle="", ax = ax)
plt.title("$f(t)=sin(t)$");
  • ここでは、サイン関数を渡して学習データをサンプリングしている
    • 他の３つの関数の学習も基本的な操作は同じなので割愛する
      • 気になる場合はコード全文を参照

結果

  • image.png
  • image.png
  • image.png
  • image.png
  • どれも教科書のようにいい感じに学習できているようにみえる

その他

  • 教科書の内容を一通り読み終えて、勉強会としては終了した！
    • 最後の方の変分問題あたりのコードも余裕があれば記事にしたい

バックナンバー

参考文献

モデルベース深層学習と深層展開 森北出版(刊) 和田山 正(著)

0
0
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
0
0

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?