Go to Qiita Advent Calendar 2024 Top
LoginSignup
0
0

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?

@gomi-kuzu

『モデルベース深層学習と深層展開』読み会レポート#8

Last updated at Posted at 2024-09-09

$\def\bm{\boldsymbol}$

概要

  • オンラインで開催している『モデルベース深層学習と深層展開』読み会で得られた知見や気づきをメモしていく
  • ついでに、中身の理解がてらJuliaサンプルコードをPythonに書き直したコードを晒していく
    • 自動微分ライブラリにはJAXを使用する

第8回

大まかな内容

  • 有限データサイズで学習するときの話
  • 無線通信の信号処理分野における深層学習

議論になったこと

4.4.1節 あたり

  • データセットのサイズと汎化誤差の関係の検討って具体的に何？
    • データ減らしていったときに、汎化性能がガクッと落ちるラインがどの辺からかとか？
      • でも、結局少数のデータしかないときと、いっぱいある時って極端な事も多いよねー
  • サンプルコード眺めながら
    • 学習率が個別にチューニングされてるけど、エポックは固定だからなんか不公平感…

5.1.2節 あたり

  • 無線通信におけるMIMO(Multiple-input multiple-output)システムとは？
    • 送信側も受信側もアンテナが複数あって、同時に複数の信号を送って受け取るようなやつ

5.1.3節 あたり

  • 式(5.5)はどっから出てきた？
    • 自乗誤差の最小化から来てるっぽいが、$\bm{H}$が実数じゃなくて複素行列なのがポイントかも？（宿題）

5.1.4節 あたり

  • 信号点配置とは？
    • 複素平面で、振幅と位相の組わせで信号の種類を特徴づける。特徴量っぽいもの？
  • 問題設定としては、復元がしやすい信号点配置の自動生成器を学習によって得る問題
    • 違う信号に対応する信号点同士が複素平面上でいい感じに分離できている事が目指す姿
      • 学習データは式（５．２）を使わずに、適当に1hotベクトルを生成してるのは、最終的に作りたいのが信号点配置で、外から見ると単純な分類問題になるから？
      • 送信機受信機が存在してる時点で、信号点配置は決まっているのでは？（どこに実用性がある？）
        • ->設計時のモデルがあったとしても、$\bm{H},\bm{w}$が環境によって変わる事はありそうで、その辺がデータからフィッティングできるみたいな話？

5.1.5節 あたり

  • P117真ん中あたりの、「ニューラルネット方式では送信信号が二値信号であるという事前情報が有効に活用さているものと考えられる」てのは、NNの活性化関数にtanhを選んだことを指している？
    • ->たぶんそう
  • モチベがいまいちわからん
    • ->サンプルコードだと$\bm{w}$の生成される分布が分かってる問題設定だが、分布は分からないがデータはサンプリングできるみたいな状況が現実的でそれなら使えそうかも？

個人的な気づきなど

  • 5.1.4の問題設定がよく分かってなかったが、議論でイメージがついた。（信号点配置の自動設計問題）
  • 式(5.2)と式(5.6)は同じ式だが、中身は結構違う。
    • （５．２）の方では送信側の設計に閉じてて、（５．６）の方は、送信機からの信号を受信機側でどう扱うかみたいな話につながる。

プログラムでの理解

  • 今回の範囲では、AWGN通信路上で通信する際の信号点配置の自動設計問題にオートエンコーダを活用する方法を学んだ
    • ちなみにこれは深層展開ではなく、割と純粋なモデルベース深層学習の一例となっている
  • 和田山先生公開のサンプルプログラムをPythonで再現する
  • プログラムの全文はこの辺に上げている

問題設定

  • MIMO通信システムにおいて、適切な信号点配置を自動設計したい
    • つまり、$m$種類の信号をなるべく複合しやすいように複素平面に埋め込みたい
    • 実は前回までに扱ったスパース信号再生成問題とほぼ同じモデル化を行う
      • 以下の線形観測を仮定
        • $\bm{y}=\bm{Hx}+\bm{w}$
          • 観測ベクトル$\bm{y}\in \mathbb{C}^m$から送信ベクトル$\bm{x}\in\mathcal{S}^n$を推定する
            • $\mathcal{S}\subset\mathbb{C}^2$は信号点配置を表現する複素数の集合である
            • $\bm{H}\in\mathbb{C}^{m \times n}$はチャンネル行列と呼ばれる、送受信アンテナ間の線形干渉を表す複素行列
            • $\bm{w}\in \mathbb{C}^m$は複素雑音
      • 上記の逆関数をオートエンコーダを使って取得する
        • これは、符号化器と複合化器のくびれの部分が複素平面の信号点配置空間になっていて、信号ラベルの再生成誤差から両器を学習させれば、符号化器が所望の逆関数の近似になっているというアイデアである
          • $\bm{y}$は信号の種別をラベル的に表現できればいいので、1hotベクトルで定義する
          • オートエンコーダなので、入出力に同じデータを用いて学習を行う
          • 符号化の自由度が高すぎると複素平面上で好き勝手に配置が離れていく可能性があるので、適当な正規化が必要になる
            • 教科書の例ではピーク電力制限というものをかけている
              • 具体的にはバッチデータを以下で割る
                • $\sqrt{max(\sum_i{x_i^2}})$
                  • maxはバッチ中の最大をとっている

Pythonで実装

必要ライブラリインポート

import numpy as np
import jax
import jax.numpy as jnp

from jax.example_libraries import optimizers
from tqdm.notebook import trange
from functools import partial
from flax import linen as nn
from flax.experimental import nnx
from typing import Sequence, Callable, Tuple
  • Flaxを使ってNNを記述する

問題設定

M = 32
K = 100
num_hidden_units = 10 
sigma = 0.1
  • 32種類の信号を仮定

学習データ生成関数の定義

def mini_batch(K):
    r = np.zeros((K, M))
    row = np.array(range(K))
    col = np.random.randint(0, M, K)
    r[row, col] = 1
    return jnp.array(r)
  • 乱数で1hotベクトルをバッチサイズ分作る

符号化器と復号化器クラスの定義

class Encoder(nn.Module):
    hidden_dim : int
    normalizer : Callable
    act_fn : Callable = nnx.relu
    
    @nn.compact
    def __call__(self, x):
        x = nn.Dense(self.hidden_dim)(x)
        x = self.act_fn(x)
        x = nn.Dense(2)(x)
        x = self.normalizer(x)
        return x

class Decoder(nn.Module):
    hidden_dim : int
    output_dim : int
    act_fn : Callable = nnx.relu
    
    @nn.compact
    def __call__(self, x):
        x = nn.Dense(self.hidden_dim)(x)
        x = self.act_fn(x)
        x = nn.Dense(self.output_dim)(x)
        x = nnx.softmax(x)
        return x
  • nn.Moduleを継承してNNモデルを定義する
    • どちらも最初に、初期化時の引数（の名前と型）をいくつか指定している
      • 符号化器の隠れ層の次元は初期化の際に与える
        • ただし、入力層の次元は指定しておらず、初めてデータを流し込んだときに決まる点に注意
      • 符号化器は引数として正規化関数を受け取り、正規化に用いる
  • FlaxではNNモデルの書き方がいくつかある
    • @nn.compactデコレーターを付けて__call__()を定義するのはそのひとつ
      • setup関数を定義する方法もあるが、コチラのほうが気楽に書けるイメージ…
  • どちらもあまり大した構造はしていない
    • それぞれ、二回全結合層と活性化関数を経由して信号が伝達される

信号路モデルの定義

class ChannelModel(nn.Module):
    hidden_dim : int
    output_dim : int    
    normalizer : Callable
    sigma : float
    act_fn : Callable = nnx.relu

    def setup(self):
        self.encoder = Encoder(hidden_dim = num_hidden_units, normalizer = self.normalizer)
        self.decoder = Decoder(hidden_dim = num_hidden_units, output_dim = self.output_dim)
    
    @nn.compact
    def __call__(self, x):
        x = self.encoder(x)
        x = x + self.sigma * jnp.array(np.random.randn(K, 2))
        x = self.decoder(x)
        return x
## ピーク電力制限の正規化関数
def peak_const(x):
    return x/jnp.sqrt(max(jnp.sum(x**2, axis=1)))

x = mini_batch(K)
#学習モデルのインスタンス作成
channel_model = ChannelModel(hidden_dim=num_hidden_units, output_dim=M, normalizer=peak_const, sigma=sigma)
#パラメタの初期化
key = jax.random.PRNGKey(0) 
params = channel_model.init(key, x[:1])["params"]
# ダミーデータの仮伝搬
channel_model.apply({"params":params}, x).shape
  • 符号化器と復号化器を組み合わせてひとつの信号路を表現する
  • 符号化した後にノイズ$\bm{w} \sim\mathcal{N}(\bm{0},\bm{I})$を全てのミニバッチに足し合わせている（AWGN通信路モデルの再現）
  • nn.Moduleクラスはapply()を使って順伝搬(推論)を行う。
    • このとき、使うパラメタを引数で指定する
    • methodという引数を使ってメソッドを指定できるが、なにも指定しなければ__call__()になる

誤差関数の定義

@jax.jit
def get_dot(x):
    return x @ x.T
batch_get_dot = jax.vmap(get_dot, in_axes=0, out_axes=0)
def loss_func(X, params):
    pred = channel_model.apply({"params":params}, X)
    loss = jnp.mean(batch_get_dot(pred - X))
    return loss
  • 元データと復元データの２乗誤差を元にバックプロパゲーションを行う

学習

adam_lr = 1e-2
train_itr = 5000

opt_init, opt_update, get_params = optimizers.adam(adam_lr)

def step(x, step_num, opt_state):
    value, grads = jax.value_and_grad(loss_func, argnums=-1)(x, get_params(opt_state))
    new_opt_state = opt_update(step_num, grads, opt_state)
    return value, new_opt_state

def train(params):
    opt_state = opt_init(params)
    for itr in trange(train_itr, leave=False):
        x = mini_batch(K)
        value, opt_state = step(x, itr, opt_state)
        print("\r"+"\rloss:{}".format(value), end=" ")
    return get_params(opt_state)

trained_params = train(params)
  • 学習の大まかな流れはこれまでと同じ
  • パラメタの最適化ソルバーもこれまで使ってたjax.example_librariesに入ってるものを使う
    • 好みに応じてoptaxなどを使うこともできる

学習後のエンコードテスト

#復号化器をもう一つ作成
enc = Encoder(hidden_dim=num_hidden_units, normalizer=peak_const)
#適当な入力を作成
test_x = mini_batch(K)
#学習済みパラメタを使ってエンコード
out_x = enc.apply({"params":trained_params["encoder"]},test_x)

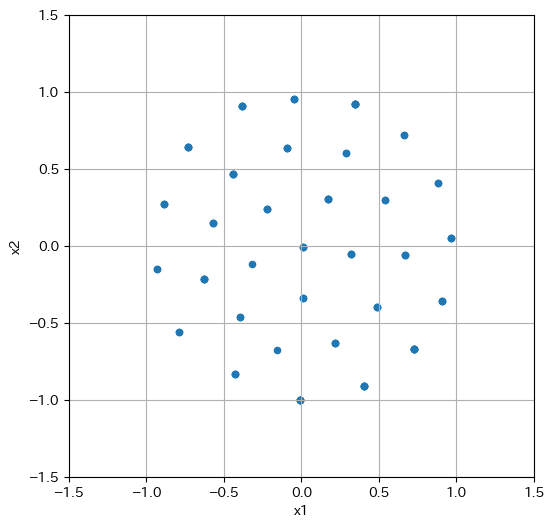
結果

image.png

  • 教科書と同じような信号点配置の図が得られた
    • パワーの制約内で、いい感じに分離された信号点配置が得られている

その他

  • 今回、人数は少なかったが結構実りのある議論ができた
    • でも、参加者がもうちょっと増えたら嬉しい^^;

バックナンバー

参考文献

モデルベース深層学習と深層展開 森北出版(刊) 和田山 正(著)

0
0
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
0
0

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?