概要
- オンラインで開催している『モデルベース深層学習と深層展開』読み会で得られた知見や気づきをメモしていく
- ついでに、中身の理解がてらJuliaサンプルコードをPythonに書き直したコードを晒していく
- 自動微分ライブラリにはJAXを使用する
第0回
大まかな内容
- モデルベース深層学習と深層展開の概説
- 上記がどんな事に応用可能か
- 微分可能プログラミングとしての実現方法について
議論になったこと
1.1.1節 あたり
- モデル駆動アプローチの実例
- 制御だと運動の法則等からモデリングする
- 通信だと、電波や媒質(空気など)を支配する法則からモデリング
- アンテナなど部品は物理系の法則
- 通信だと周波数領域のパラメタの同定に学習要素があるかも
- 図1.1を眺めながら
- 真ん中の図はNNの重みも学習可能パラメータでは?
- おそらくそう。NN以外の計算に埋め込んだパラメタもNNのパラも同時に組み込める的な事を表現しているのでは
- 真ん中の図はNNの重みも学習可能パラメータでは?
1.1.2節 あたり
- なぜ”微分可能”が重要なのか
- 勾配ベースの方法を使った最適化をするために必要
- 勾配法以外もやり方はあるが、なんやかんや勾配法は速いし複雑な問題も割とシンプルに解ける
- 個々が微分可能なものの集まりは全体で微分可能って性質も強い
- 勾配ベースの方法を使った最適化をするために必要
1.1.3節 あたり
- 図1.3を眺めながら
- 左下の”系の支配方程式”の$\alpha,\beta$が学習パラメータということなのか
- そういう場合もあるし、式自体が書き下せない場合もあるのでは
- この学習は普通の深層学習と何が違うのか
- モデルベースだと、パラメータ数が圧倒的に少なく学習が収束しやすいのでは
- 動的システムのオンライン学習にも向いている
- モデルベースだと、パラメータ数が圧倒的に少なく学習が収束しやすいのでは
- 左下の”系の支配方程式”の$\alpha,\beta$が学習パラメータということなのか
1.1.4節 あたり
- 爆発を伴う場合などの不連続な系についての流体力学シミュレーションにもモデルベース深層学習は適用できるのか?
1.2.1節 あたり
- 条件分岐って、本当に他の一般的な自動微分ライブラリでも対応してんの?
1.2.2節 あたり
- 微分対象の変数で定義した条件分岐をさせても導関数が取得できるのか?(不連続で無理とかならない?)
- やってみたらできた
個人的な気づきなど
- 一人だと図を深く考えずに読み流してる事が多かった。改まって参加者の方々と議論して気づけた事があってよかった。
- 会の後の雑談の中で、Juliaのサンプルコードを弄って遊んでいると、結構無茶な分岐についてもエラーなく微分してくれいて、「逆にどんな風に関数を定義するとまずいんだろう」的な話題になった。その場ではナアナアにしてしまったが、後で考えると、「エラーなく微分が実行出来ること」と、「それを元に勾配法がうまく収束するか」は、別問題だがごっちゃにして話てたかもと思った。今後の勉強会で機会があればその辺議論したい。
プログラムでの理解
問題設定
sin関数のマクローリン展開
$$
\sin(x) = x - \frac{x^3}{3!} + \frac{x^5}{5!} - \cdots+(-1)^i\frac{x^{2i+1}}{(2i+1)!}+\cdots
$$
を$i=n$の項までで打ち切った、打ち切り関数を実装し、その(プログロムの意味での)関数の自動微分とcos関数の出力を比較してみる
Pythonで実装
必要ライブラリインポート
import jax
import math
自動微分にはJAXを用いる
打ち切り関数の定義
nの値は教科書と揃えてある
def tsin(x):
sum = 0
n = 8
for i in range(n):
if i%2 == 0:
sum += (1/math.factorial(2*i+1))*x**(2*i+1)
else:
sum -= (1/math.factorial(2*i+1))*x**(2*i+1)
return sum
※今回はオリジナルのJuliaコードになるべく合わせる意味でもif文で記述したが、jitコンパイラを使いたい場合はifをnp.whereで置き換える。また、階乗の計算もmathライブラリよりjax.scipy.spatialに収録されたものを使ったほうがいいかもしれない。
微分した関数の取得
d_tsin = jax.grad(tsin)
これで、sinの微分であるcosの近似関数が得られる
図示
適当な等差数列で入力を作成し、numpyのcos関数と比較する
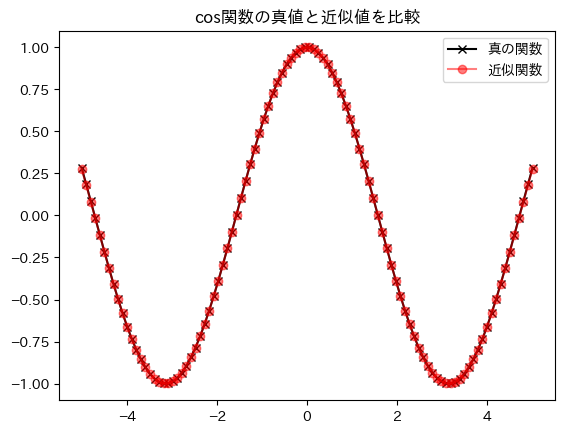
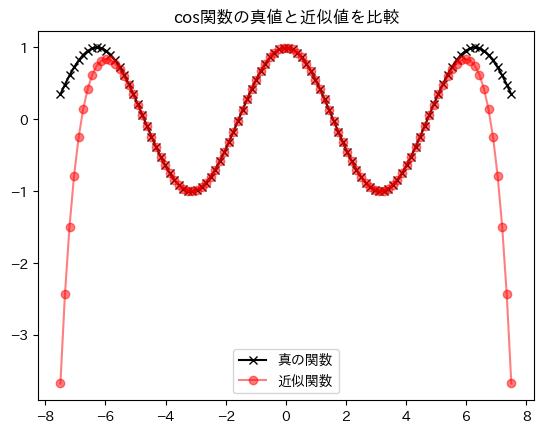
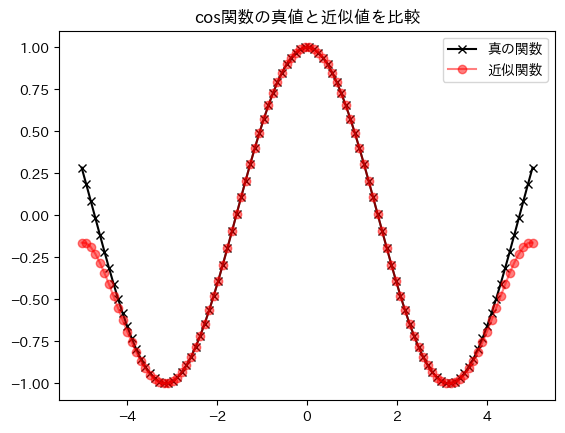
教科書と似たような出力を得られた!
余談
実は、サンプルプログラムの$x$の値域と打ち切り次数$n$は絶妙で、少し設定を変えてプロットすると以下のようになる。(マクローリン展開は0付近での近似なので、当たり前ではある)
値域を1.5倍にしてみる
n=6にしてみる
その他
- Zygoteは「ざいごーとぅ」と読むらしい…