$\def\bm{\boldsymbol}$
概要
- この度始まる『モデルベース深層学習と深層展開』読み会を前に、”深層展開”の世界観を整理してみる
- どんなことに使えそうか、個人的な期待を綴ってみる
深層展開とは
参考書のまえがきには
深層展開(deep unfolding)は,反復アルゴリズムに対してモデルベース深層学習技術の考え方を適用した,アルゴリズム構成のための方法論である.
とある。さらに、
反復アルゴリズムの信号処理プロセスを時間方向に展開(folding)することで,深層ニューラルネットワークモデルに類似したネットワークモデル(信号流グラフ)が得られる.アルゴリズムに含まれる部分処理が微分可能であれば,ミニバッチ学習法などの標準的な深層学習技術を適用することで,反復アルゴリズムの内部の学習可能パラメータを調整することが可能となる.
と続く。つまり、こういう事ではなかろうか。
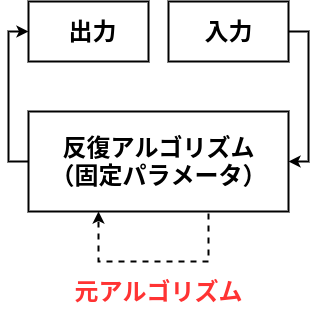
👆こういう一般的なアルゴリズムを時間方向に展開し、さらに学習可能パラメータを埋め込むことで、
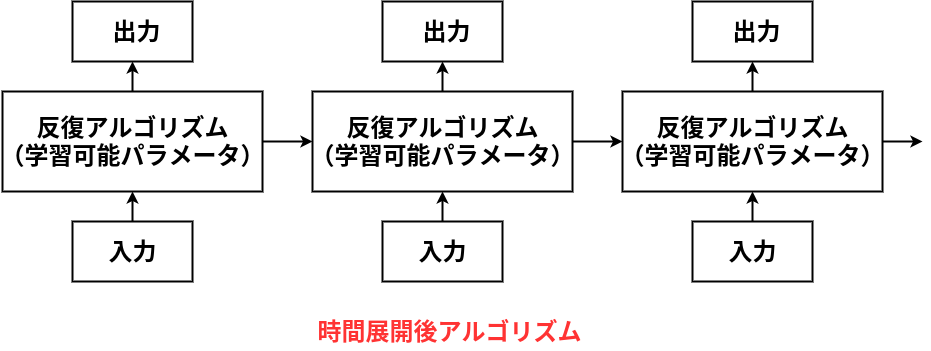
👆このような、層の深いネットワークを作る。
この解釈が正しいかは、読み会で議論したいところであるが、少し観点を変えながらこの図を眺めてみる。
制御工学的観点
展開前の図の入力と出力の箱をひとつの箱にして、制御対象とみなせば、制御工学におけるフィードバックループの図とみなせる。反復アルゴリズムは、そのまま制御コントローラになる。
更に、出力をもとにパラメータを更新していくことを制御工学のブロック線図的に表現すると以下のようになる。
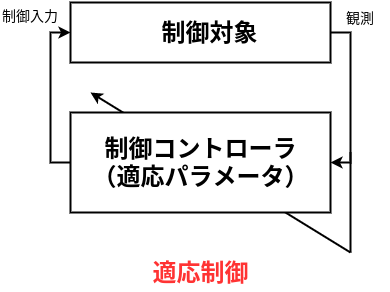
これは、制御工学における”適応制御”の概念を示す図にそっくりである。なんと、深層展開とは適応制御なのか!?
機械学習的観点
時間展開後の図をみると、ニューラルネットワークを少しかじった人ならすぐに思うかもしれない。「リカレントニューラルネットワークかな」
”反復アルゴリズム”の箱とそこから出る矢印の具体的な計算は、行列演算と活性化関数といったNN的なものに限らないため、両者は厳密に同じものというわけではない。しかし、構造が似ているため、学習可能パラメータの更新則には、近年めざましい成果を上げてきたNN研究のアイデアが流用できるであろう事は想像に難くない。なんと、深層展開とは結局、深層学習のことなのか!?
俯瞰すると…
少し、落ち着いて技術を俯瞰してみる。とりあえず、「深層展開とはまるっきり何もかも新しい技術!」というわけではなさそうだ。しかし、それはネガティブな意味で言っているわけではない。これまで、様々な場面で使われていた固定パラメータを使った反復アルゴリズム(制御コントローラはその一例)の中に学習可能パラメータさえ仕込んでしまえば、なんとまあ皆大好き深層学習とみなせるようになる。そういう、異なる考え方の融合的なものがこの手法の肝であり良さではなかろうか。
また、「固定パラメータを使った反復アルゴリズム」の”固定パラメータ”がこの本における”モデル”を指していると思われる。モデルは対象の系のドメイン知識が詰まったものである。精度のよいモデルさえあれば、系を操るのはたやすい一方で、それを常に手に入れるのは難しい。そのため、逆に初期の深層学習では、モデルを持たずに大量のデータを用いて精度と汎化性を確保していた。
…結局の所、深層展開はモデル駆動アプローチとデータ駆動アプローチの”いいとこ取り”を目指した手法である。ドメイン知識をモデルを通して取り込みつつも、それにまるっきり頼るわけではなく、モデルの一部のパラメータをデータから修正していく事で、モデル化誤差を動的に解消していく事ができるというわけだ。
偉そうに書いたが、この辺は参考書の1章に書かれた事をそれっぽく要約しただけというのが実のところである。更に多くの事は読み会で議論できる事を願う。
何に使える技術なのか
ここからは、読み会を通して、どんな事ができるようになったら嬉しいか、初心を書き記しておく。端的には以下である。
- モデルベース制御における”モデル化誤差”の解消をスマートに行えるようになりたい
モデルベース制御器とモデル化誤差の簡単な例
簡単な数値シミュレーションを通して、制御問題の課題を示す。
以下のような、マスバネ系を考える。$m$は質量、$k$はバネ定数、$f$は外力である。
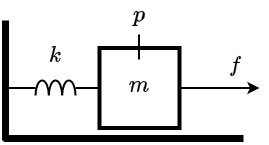
この系は位置$p$を使って、$\bm{x}=[p~~\dot{p}]^T$と状態量を定義したとき
\dot{\bm{x}}=A\bm{x}+B
f
A=
\begin{bmatrix}
0 & 1 \\
-\frac{k}{m} & 0
\end{bmatrix}
,
B = \begin{bmatrix}
0 \\
\frac{1}{m}
\end{bmatrix}
と状態空間表現できる。(詳細は割愛)
この系は(摩擦のような)散逸項を持たないので、$f=0$の自由応答では、平衡点($\bm{x}=\bm{0}$)以外から運動を始めれば、以下のように、無限に振動を続ける。(システムの固有値が安定境界上にある)
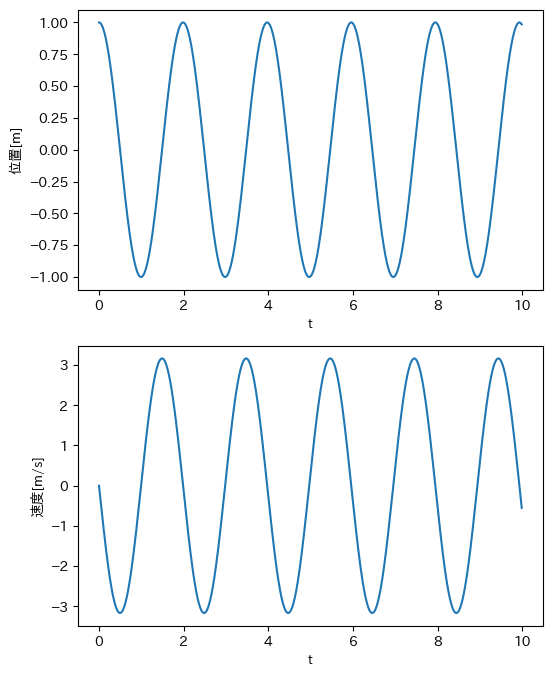
これを、$\bm{x}=\bm{0}$の状態に収束させるために、フィードバック系を組む方法は無数にある。
これも詳細は割愛するが、モデルベースの有名な方法にLQR法というものがあり、以下のリッカチ方程式の解$P$を使って
A^TP+PA+Q-PBR^{-1}B^TP=0
$f = -R^{-1}B^TP\bm{x}$ とすれば、良いことが分かっている。($Q,R$はユーザが任意に決める最適性のパラメータ)
ここで、コントローラのフィードバックゲイン$-R^{-1}B^TP$を決めるための式にモデル$A,B$が登場する。この問題では、とても簡単な系なので、真のモデルパラメータが求まるかもしれないが、実際の制御問題ではそうはいかない。
以下は、ある適当な$Q,R$を設定したときの、真のモデルを使ったLQR法とモデル化誤差をあえて含めたときのLQR法の応答のシミュレーションである
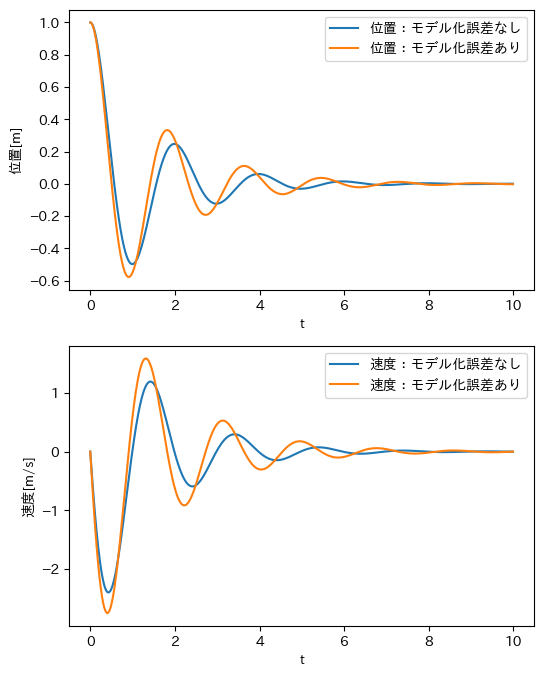
モデル化誤差がある場合は、ない場合に比べて、オーバーシュートが大きくなったり、整定時間が長くなっている。
このようなモデル化誤差の制御への影響は、もっと複雑な制御問題にも必ず現れ、その解決方法は様々あるのだが、深層展開はその方法の(スマートな)ひとつになりうると期待している。
結論
深層展開がどれくらい使える技術なのかは、本当の所まだわからない。読み会を通して理解を深めていきたい。