『モデルベース深層学習と深層展開』読み会レポート#6

$\def\bm{\boldsymbol}$

概要

• オンラインで開催している『モデルベース深層学習と深層展開』読み会で得られた知見や気づきをメモしていく
• ついでに、中身の理解がてらJuliaサンプルコードをPythonに書き直したコードを晒していく
  • 自動微分ライブラリにはJAXを使用する

第6回

大まかな内容

• 不動点反復式とは
  • 逆問題の対象にする系が特定の条件を満たし、観測値を使って繰り返し更新計算をすることで解が導ける場合の反復式
• より早く不動点に収束させる手法としてSOR法がある
  • この中のパラメータを深層展開で学習するのがDU-PSOR法

議論になったこと

4.1節の最初 あたり

• 冒頭の「適切な条件が満たされる場合」とは？
  • ->その直後の話を指してる？
• P85最初らへんの、「関数が縮小的である」とは？
  • 制御工学だと、状態方程式の線形写像の固有値の絶対値が１以下とか？（離散の場合）
  • 数学的にはこれのことっぽい→■

4.1.1節 あたり

• 式(4.4)のすぐ下の「初期点が不動点の近傍にある」って条件は何に付随して出てきた？
  • ->無限遠点とかから始めるような初期条件を除いている？

4.1.2節 あたり

• 問題アンサンブルの話の世界観はP54の3.2.1節らへんと同じ
  • ここでは更新関数の関数形が何らかの確率分布に従って生成されるみたいなこと

4.1.3節 あたり

• 式(4.30)->(4.31)の式変形はどこから来てる？
  • L-pノルムに対する基本性質->■
• 式(4.36)はどういう事を言っている？
  • ->$t$が進む毎に残差が減っていく$q$が小さいほど速度が速い
    • $q$は$\beta$から、$\beta$は$\omega$から決まってるという関係
• 式(4.27)だと眺めると、$T$が$n$より大きいときは一通り$1/\lambda$を$\omega$に並べとけば$\beta(\lambda)$は全ての$\lambda$に対して０になりそうじゃない？

4.1.5節 あたり

• P91の最終段落、$\bm{A}$の条件が4.1.3節の式（4.16）の下のときとは異なっているように見えるが、どういう意図？
  • ->ソースコード見ると4.1.3節の説明準拠で実装しているように見えるので、単純に”正定値”って書き忘れただけでは？
• ソースコードの確認
  • 理論値は$\omega$に対して式(4.27)で$\beta(\lambda)$の数列を作って最大値とって式（4.35）で$q$計算して初期値から掛けていくって感じで算出

4.1.6 節あたり

• $\bm{P}$が固定の範囲内で任意の連立方程式の求解に使えるのか？
  • あくまで、例として扱っているだけで、実用性のある問題設定ではない説…

個人的な気づきなど

• 式(4.30)->(4.31)の式変形はコーシー・シュワルツの不等式由来かと思っていたが、違うっぽいこと教えてもらえた（上記のL-pノルムの性質の話）

プログラムでの理解

• 今回の範囲では、観測値から潜在変数を推定する”逆問題”を解く手法のひとつに深層展開を適用した
• 和田山先生公開のサンプルプログラムをPythonで再現する
• プログラムの全文はこの辺に上げている

問題設定

• 状態量$\bm{x}$に対して観測方程式$f(\bm{x})=\bm{Ax}+\bm{b}$で観測される量がある
  • $\bm{A},\bm{b}$は問題アンサンブルのインスタンス生成時に与えられるとする
    • （実装時は$\bm{A}$を最初に固定、$\bm{b}$が$\mathcal{N}(\bm{0},\bm{I})$に従って都度生成してる）
• このとき、$f(\bm{x})$の値をもとに、反復解法を用いて$\bm{x}$に辿り着くことを考える
  • もし、初期値$\bm{x}^{(t=0)}$が辿り着きたい値の近傍にあるなら
    • $\bm{x}^{(t+1)}=\bm{Ax}^{(t)}+\bm{b}$を繰り返し行うことで、不動点$\bm{x}^*$に辿り着くことができる
• PSOR法では、以下のようにすることで、より速く不動点に収束する
  • $\bm{x}^{(t+1)}=\bm{x}^{(t)}+\omega(\bm{Ax}^{(t)}+\bm{b}-\bm{x}^{(t)})$
    • $\omega$は行列$\bm{I}-\bm{A}$の最大固有値$\lambda_{max}$と最小固有値$\lambda_{min}$を使って、$\omega=2/(\lambda_{max}+\lambda_{min})$とする
• 深層展開を使ったDU-PSOR法では、$\omega$を適当に生成した$\bm{b}$を使った学習により獲得することで、新たに$\bm{b}$が与えられても、より速く不動点に収束する

Pythonで実装

必要ライブラリインポート

import numpy as np
import numpy.linalg as LA
import jax
import jax.numpy as jnp
import jax.numpy.linalg as JLA
from jax.example_libraries import optimizers
from tqdm.notebook import trange
from functools import partial

問題設定（定数の設定）

n = 8
num_itr = 40
K = 50
A = np.random.randn(n,n)
A = A.T @ A
A = A/LA.norm(A)
eig, _ = LA.eig(np.eye(len(A)) - A)
A = jnp.array(A)
lambda_min = min(eig)
lambda_max = max(eig)
omega_opt = 2/(lambda_min + lambda_max)

• 4.1.3節で言ってた条件を満たす$\bm{A}$を生成している
  • 乱数で生成した$\bm{A}$についてA = A.T @ Aとして、$\bm{A}$が正定対称行列になるようにしている
    • 参考
  • さらに、A = A/LA.norm(A)の処理によって、全ての固有値を１以下にしている
    • LA.norm(A)はフロベニウスノルムだが、実対象行列に対しては固有値の絶対値のMax（スペクトル半径）に等しい
    • 行列全体をLA.norm(A)で割ることで固有値も$1/|\lambda_{max}|$でスケーリングされて１以下になる

ミニバッチ生成関数の定義

@jax.jit
def gen_x_fixed(b):
    return JLA.inv((np.eye(len(A)) - A)) @ b
batch_gen_x_fixed = jax.vmap(gen_x_fixed, in_axes=-1, out_axes=-1)

• 与えられたベクトル$\bm{b}$のバッチに対して、$\bm{x}=\bm{Ax}+\bm{b}$を満たすようなベクトル$\bm{x}$のバッチを返す関数

DU-PSOR反復の定義

@partial(jax.jit, static_argnums=1)
def DU_PSOR(b, max_itr, omega, T):
    x = np.zeros((n, K))
    for i in range(max_itr):
        k = (i % T) + 1
        x += omega[k] * (A@x + b - x)
    return x

損失関数の定義

@jax.jit
def get_dot(x):
    return x @ x.T
batch_get_dot = jax.vmap(get_dot, in_axes=-1, out_axes=-1)

@partial(jax.jit, static_argnums=2)
def loss(x_fixed, b, max_itr, T, omega):
    x_hat = DU_PSOR(b, max_itr, omega, T)
    return np.sum(batch_get_dot(x_fixed - x_hat))/K

• 最近になってこの辺、わざわざベクトル毎の内積を返す関数をバッチ化しなくてもjax.numpy.linalg.norm()で同等（正確にはそのルート）のものが得られるとわかったが、これを書いたのは少し前なのでそのままにしている（そのうち修正するかも）

訓練関数の定義

max_inner = 40
train_depth = 10
adam_lr = 0.1

opt_init, opt_update, get_params = optimizers.adam(adam_lr)

@partial(jax.jit, static_argnums=2)
def step(x_fixed, b, max_itr, T, step_num, opt_state):
    value, grads = jax.value_and_grad(loss, argnums=-1)(x_fixed, b, max_itr, T, get_params(opt_state))
    new_opt_state = opt_update(step_num, grads, opt_state)
    return value, new_opt_state

def train(omega, T):
    opt_state = opt_init(omega)
    for itr in trange(train_depth, leave=False):
        for i in range(max_inner):
            b = jnp.array(np.random.randn(n, K))
            x_fixed = batch_gen_x_fixed(b)
            value, opt_state = step(x_fixed, b, itr+1, T, i, opt_state)
        print("\r"+"\rloss:{}".format(value), end=" ")
    return get_params(opt_state)

• ここ数回やってる実装からみて、新しいことはやってない…

学習と評価

T = 2
omega_init = np.ones(T)
omega_trained = train(omega_init, T)

def comp_mse_DUPSOR(max_itr, omega, T):
    b = jnp.array(np.random.randn(n, K))
    x_fixed = batch_gen_x_fixed(b)
    return loss(x_fixed, b, max_itr, T, omega)

DUPSOR_mse = [comp_mse_DUPSOR(i+1, omega_trained, T) for i in range(num_itr)]

• Tを変更するとどうなるかも気軽に試せる

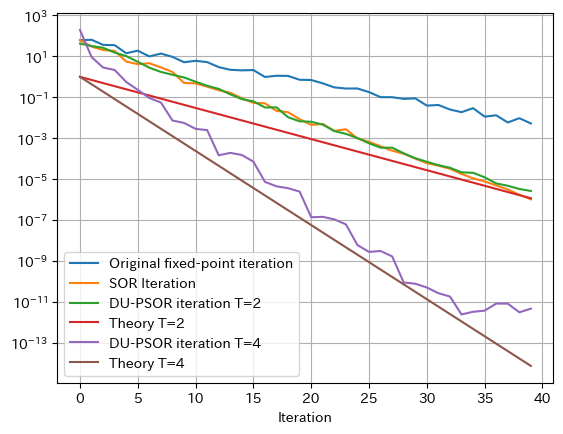
結果

• 教科書同様、Tを変えたりした結果や理論値と比較している
  • T=2のときは教科書程良い結果にはならなかった。。。？

その他

• 細かい所気にしすぎて、いつにも増して牛歩になってしまった…

バックナンバー

• 『モデルベース深層学習と深層展開』読み会 レポート（開催前準備編）
• 『モデルベース深層学習と深層展開』読み会レポート#0
• 『モデルベース深層学習と深層展開』読み会レポート#1
• 『モデルベース深層学習と深層展開』読み会レポート#2
• 『モデルベース深層学習と深層展開』読み会レポート#3
• 『モデルベース深層学習と深層展開』読み会レポート#4
• 『モデルベース深層学習と深層展開』読み会レポート#5

参考文献

モデルベース深層学習と深層展開 森北出版(刊) 和田山 正(著)