Go to Qiita Advent Calendar 2024 Top
LoginSignup
0
0

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?

@gomi-kuzu

『モデルベース深層学習と深層展開』読み会レポート#10

Posted at

$\def\bm{\boldsymbol}$

概要

  • オンラインで開催している『モデルベース深層学習と深層展開』読み会で得られた知見や気づきをメモしていく
  • ついでに、中身の理解がてらJuliaサンプルコードをPythonに書き直したコードを晒していく
    • 自動微分ライブラリにはJAXを使用する

第10回

大まかな内容

  • 平均合意プロトコルに対する深層展開
  • オイラー法と深層展開による微分方程式モデルのフィッティング

議論になったこと

5.4.3節 あたり

  • 空手クラブのデータセットは、結構他の教科書とかでも見たから定番なのかも
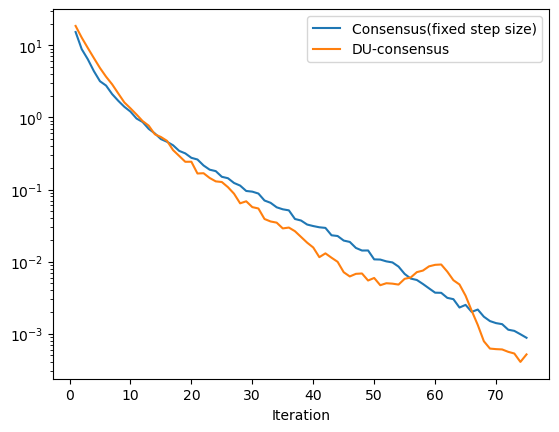
  • 図5.11は提案手法が結構不安定に見えるが原因なんだろう…
  • サンプルコード回しながら
    • グラフの誤差が上がる部分は毎回挙動が変わる
      • やはり、この不安定さはよくないのでは？
        • 対数グラフでこの上下の仕方は結構でかい
    • iterationを増やして回してみると、深層展開なしのパラメタ固定値の方が、順調に下がっていったのに対し深層展開ありだと、かなりでかい誤差の爆発が起きるタイミングが現れた
      • また、最終的に収束するときの誤差もお個位置の平均合意プロトコルの方が低かった…
    • 今回はそもそも問題が簡単すぎて、メリットが出にくかった説？
      • ちなみに、平均合意問題ってそもそも問題としてどんくらい難しいのか？
        • ->答え出ず

5.5.2節 あたり

  • 微分可能にならない計算の例は、前回の範囲で出た純粋なビリーフプロバゲーション複合の際のチェックノード・変数ノード処理とか

6.1.1節 あたり

  • 微分方程式の近似解法の陽的・陰的ってなんだっけ？
    • 陽的：元の速度の式を使って、次のステップの位置を求めて、そこでまた速度を求めて…を繰り返すカンジの手法
      • 簡単だが精度低め
    • 陰的：速度と位置をどっちもわからないものとして同時に連立方程式を解いて求める手法
      • 精度高いが複雑
    • 参考

6.1.2節 あたり

  • サンプルコード回しながら
    • DU-Euler
      • 今回は、あくまでベンチマーク的に真の関数からサンプルデータを集めているが、もし物理現象からの学習をやるとしたら、まずデータを眺めたり、ドメイン知識を使って、パラメトリックな微分方程式をモデリングし、そしてパラメタの学習という流れになる
        • 教科書の真の関数が$\text{exp}(2x_k)$で微分方程式が$\dot{x}=ax$というのは、一見天下りっぽく見えるが、「データが指数関数的な変化っぽいなー」ってとこから始めるなら妥当。
      • もし、もう少し難しい問題設定を考えるなら？
        • あえて式のモデリングに他の関数の項も用意して、学習によってその係数が０になるかとか？
          • サンプリング定理と無視して考えると、普通に過学習しちゃうケースもありそう…
    • DU-Euler-LV
      • このモデルは捕食者と被捕食者の個体数のダイナミクスをモデリングしたもの
      • 学習のイテレーションを上げるほど、[1 1]にピタッとなっていく
      • 横軸を$t$じゃなく、$x$とした相平面図を書くと固有値に応じた平衡点周りの挙動が可視化されて面白い
        • 参考
          • 今回の例は平衡点[1 1]に収束させようとしているので、理想のパラメタがどのようなものかが概算できる
            • ->なんかでもパット見その値に学習されてなかったので、あとで要確認

個人的な気づきなど

  • ロトカ-ヴォルテラ方程式がどんなものかの説明は教科書にはあまり詳しく書いてなかったので、参加者の方に教えてもらえて助かった。

プログラムでの理解

  • 今回の範囲では、平均合意プロトコルに深層展開を適用して収束を加速する方法について学んだ。
  • 和田山先生公開のサンプルプログラムをPythonで再現する
  • プログラムの全文はこの辺に上げている

問題設定

  • 複数の制御対象（マルチエージェント）の特定の状態の値を同じ値に収束させる問題を合意問題と呼ぶ
    • 自然界の近しい現状を挙げるなら、鳥の群れが速度を同じくして飛ぶようなものがある
  • エージェントをノード、通信路をエッジとすれば連結無効グラフ$G(V,E)$で表す事ができる
    • $V$はノード集合で、それぞれのノードは状態量$x_i$をもち、それらをまとめて$\bm{x}$とする
    • マルチエージェントの制御においては、全てのエージェント同士が通信路を持たず、隣接するノード同士だけが通信路を持つような場面が存在する
      • グラフ表現では、隣接集合$\mathcal{N}(i)\equiv\{j|(i,j)\in E\}$を定義して、$i$番目のノードが隣接しているノードのインデックスを保持しておく
  • このとき、グラフが特定の構造を有していれば、以下のように$x_i$を繰り返し修正すれば、$t\rightarrow\infty$で全ての$x_i$はその初期値全ての平均に収束する$\eta$が存在する（参考）
    • $x_i^{(t+1)}=x_i^{(t)}-\eta^{(t)}\sum_{j\in\mathcal{N_i}}(x_i^{(t)}-x_j^{(t)})$
  • 上記はグラフラプラシアン$\bm{L}$を使って以下のようにコンパクトに表現する事ができる
    • $\bm{x^{(t+1)}}=(\bm{I}-\eta^{(t)}\bm{L})\bm{x}^{(t)}$
  • $\bm{L}$は隣接行列の対角要素をゼロにした行列
    • 隣接行列は対角要素に接続総数、それ以外に$i,j$が隣接なら1を隣接でないなら0を埋め込んだ行列
  • 深層展開版では、$\eta$を時変$\eta^{(t)}$として、データから学習する
    • このとき学習データにはノードの初期値を乱数生成し、その平均値を算出し、ノードの要素数のサイズのベクトルにして組とする
    • 学習は、データセットの初期値に対して、上に書いた更新式を適当な回数適用した$\bm{x}$と組になっている平均値のベクトルとで平均自乗誤差を計算しそこから誤差逆伝搬をする
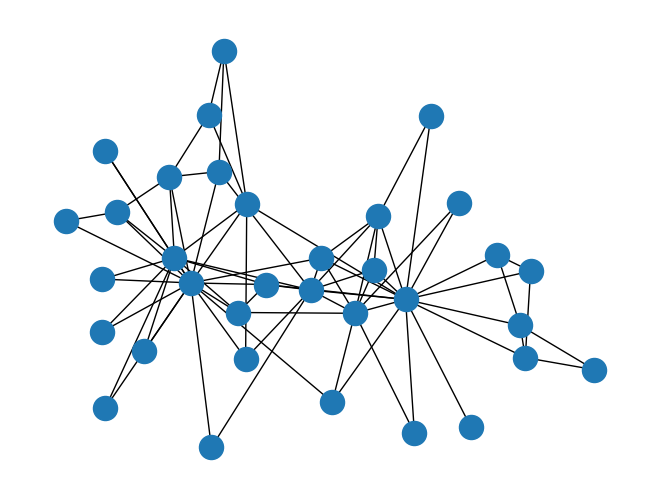
  • 今回の例題では、空手クラブデータセットを使う
    • このデータセットは、米国のある大学の空手クラブの交友関係を示したものらしい
    • image.png
      • ノードがクラブのメンバーでエッジが友好関係っぽい
    • 本来は、クラブの中での影響力を分析とかの例題に用いられるものかと思われるが、ここではあまり意味のある解析はせず、このグラフを使って合意アルゴリズムを回してベンチマーク的に使う

Pythonで実装

必要ライブラリインポート

import numpy as np
import jax
import jax.numpy as jnp

from jax.example_libraries import optimizers

from tqdm.notebook import trange
from functools import partial
import networkx as nx
  • 連結グラフライブラリとしてnetworkxを用いる(といってもデータセットのロードと隣接行列の取り出しをするのに使う程度）

準備

n = 34
g = nx.karate_club_graph()
ad_mat = np.sign(nx.adjacency_matrix(g).toarray())
dg_mat = np.diag(np.sum(ad_mat, axis=0))
L = dg_mat - ad_mat + 1e-12*np.eye(len(ad_mat))
L = jnp.array(L)
  • Lはラプラシアン
    • nx.laplacian_matrix(g).toarray()という関数でもラプラシアンが取得できそうだが、どうも変な行列が出てきたのでこうした

学習データ生成関数の定義

def mini_batch(K):
    x0 = jnp.array(np.random.randn(n, K))
    c = jnp.sum(x0, axis=0)
    r = jnp.tile(c, (n, 1))/n
    return x0, r
  • 乱数で作った行列に対して、列毎の平均を算出しその平均で埋まったベクトルを並べた行列を作る
    • イメージ)[1,2,3]と[2,2,2]が対になって、それぞれバッチサイズ分並んでるカンジ

DU-consensusの繰り返し関数と損失関数の定義

def DU_consensus(max_itr, x0, eta):
    x = x0
    for i in range(max_itr):
        x = (jnp.eye(len(L)) - eta[i]*L)@x
    return x

def loss(max_itr, x_opt, x0, eta):
    x_hat = DU_consensus(max_itr, x0, eta)
    return jnp.sum(batch_get_dot(x_opt - x_hat))/K

学習関数の定義

K = 200
num_itr = 75
adam_lr = 5e-4
max_inner = 50

opt_init, opt_update, get_params = optimizers.adam(adam_lr)

@partial(jax.jit, static_argnums=0)
def step(max_itr, x_opt, y, step_num, opt_state):
    value, grads = jax.value_and_grad(loss, argnums=-1)(max_itr, x_opt, y, get_params(opt_state))
    new_opt_state = opt_update(step_num, grads, opt_state)
    return value, new_opt_state

def train(eta):
    opt_state = opt_init(eta)
    for itr in trange(num_itr, leave=False):
        for i in range(max_inner):
            y, x_opt = mini_batch(K)
            value, opt_state = step(itr+1, x_opt, y, i, opt_state)
        print("\r"+"\rloss:{}".format(value), end=" ")
    return get_params(opt_state)
  • やってることはこれまでとだいたい一緒

学習と評価

def comp_mse_DU_consensus(max_itr, eta):
    x0, c = mini_batch(K)
    x_hat = DU_consensus(max_itr, x0, eta)
    return jnp.sum(batch_get_dot(c-x_hat))/K

eta_init = jnp.zeros(num_itr)
eta_trained = train(eta_init)
DU_consensus_mse = [float(comp_mse_DU_consensus(i+1, eta_trained)) for i in range(num_itr)]
  • 初期の$\bm{\eta}$はゼロベクトル

結果

  • image.png
    • 微妙に違うが、教科書と似たカンジの結果になった。
      • 普通の合意プロセスの方の実装はコード全文を参照

その他

  • 残りページ的に、あと1,2回で終わりそう

バックナンバー

参考文献

モデルベース深層学習と深層展開 森北出版(刊) 和田山 正(著)

0
0
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
0
0

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?