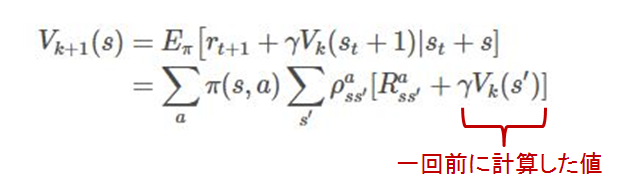【強化学習】まとめてみた 第四回（Q学習だけじゃない！動的計画法とは）

はじめに

強化学習勉強会なるものがスタートしました！
なので，それらを勉強もかねてまとめていこうと思います．二番煎じ感がものすごいですが，自分の理解度向上のためにも！
予定ではQiitaで第7回分（Q学習ぐらいまで）ぐらいやろうかなと考えています．今回は第四回です！

過去のもの

• 第一回：概要
• 第二回：n本腕バンディット
• 第三回：用語まとめ編
• 第四回：動的計画法
• 第五回（１）：モンテカルロ法（ES法）
• 第五回（２）：モンテカルロ法（方策ON型，方策OFF型）
• 第六回（１）：TD学習（ランダムウォーク）
• 第六回（２）：TD学習（Q学習・Sarsa学習）

その他リンク

• github
  https://github.com/Shunichi09/
• twitter
  https://twitter.com/ShunichiSekigu1?lang=ja
• 参考書
  http://www.morikita.co.jp/books/book/1990
• 参考書（原本）
  http://incompleteideas.net/book/bookdraft2018jan1.pdf
• 原著プログラム
  https://github.com/ShangtongZhang

原著プログラムについてですが，基本的には見ずに書いてます．
原著のプログラムが分かりにくければ，僕のgithubで見ていただけると嬉しいです．

目的

• 強化学習勉強会の内容のまとめ
• 自分の理解度向上もかねて
• プログラムの書き方の練習もかねて

おしながき

1. 前回とのつながりから～方策評価
2. 方策評価と方策改善
3. ギャンブラーの問題

前回とのつながりから～方策評価

前回のまとめとして
状態価値関数と行動価値関数を定式化し，最適状態価値関数，最適行動価値関数を定義しました

さて，強化学習において大切なのはその状態価値関数をしること（行動価値関数の場合もありますが）です
そうすれば，今自分のもっている方策$\pi$を評価できます．
そして改善へとつなげることができるのですが．．．

さて，ここからこんな風に考えます
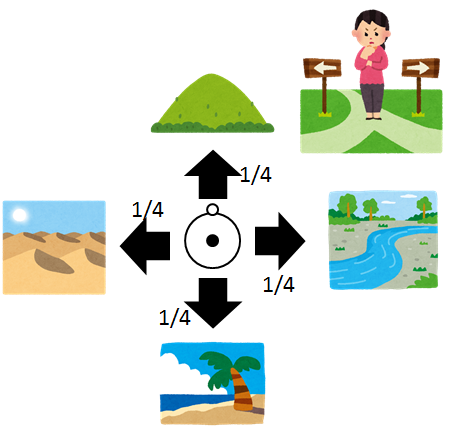
ある冒険を考えてください．
前回と同様に，今いる場所から，次へ動くときにランダム（すべて1/4で動くとします）
これで自分の行動の指針である方策$\pi$が定義できました．

では，次に気になるのがこの方策$\pi$がどれくらい正しいのかってことです
冒険でランダムに動くということは損でしょうたぶん（ラスボスの位置は決まってますので）

なので，この方策$\pi$がどれくらい正しいかを知るために，状態価値関数を方策$\pi$のもとで求めていきます．

冒険でいえば，今街にいるとして，そこからランダムに場所を選ぶとした際の街にいることの価値を求めます．

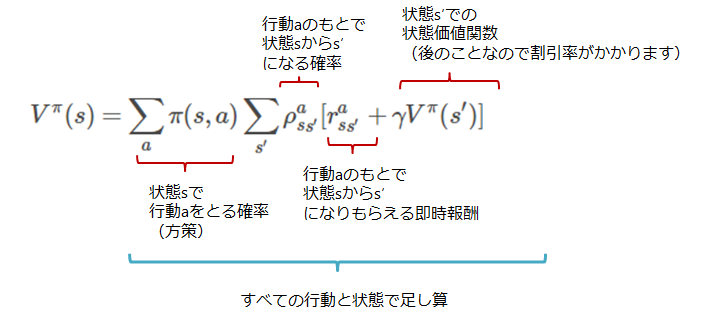
結論からいうとこの状態価値関数は以下の式で求められることになります．
今回はもはやこの式がめちゃくちゃ重要なのでそれ以外は気にしなくてもいいぐらいです

\begin{align}
V_{k+1}(s) & = E_\pi \bigr[ r_{t+1}+ \gamma V_k (s_t +1) | s_t + s] \\

& = \sum_a \pi(s, a) \sum_{s'} \rho_{ss'}^a [R_{ss'}^a + \gamma V_k(s') ]


\end{align}

いやいやどういうこと？ってなります
まず，完全にモデルが分かってるとすると，一番最初の式は状態$S$に関する式なのだから，状態の数だけ式ができて，それを解けばよいってことになりますね．
ただ，状態がたくさんある場合はやりづらくて仕方がないし，もし少ないとしても，式をいちいち立てるのはめんどくさいです．

そこで！！

さっきの近似解法を用います．
kというのは計算回数です
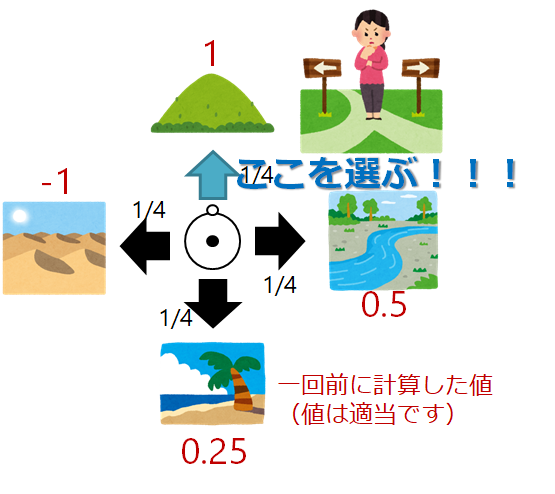
つまり，一回計算したときの値を使って次々に更新していくことで，最終的にある方策$\pi$のもとでの状態価値関数を取得できるというわけです．

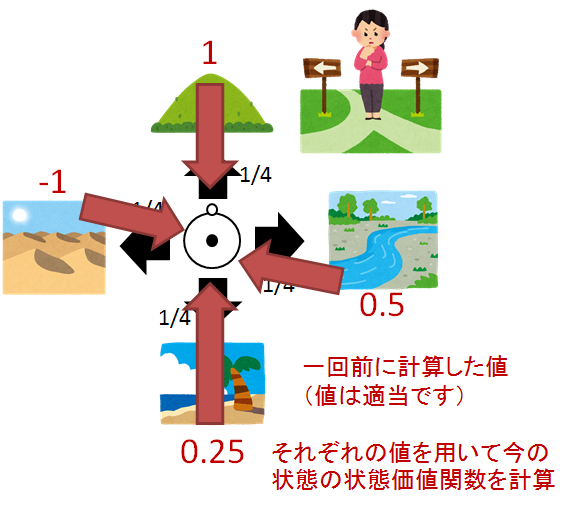
図でいうと

ということになります．

つまり作業としては，何回も何回もある方策$\pi$にのっとって計算しまくり，各状態の暫定の状態価値関数を求めていきます．そうすれば，自然とすべての値が更新されていき．．．いつのまにか，ある方策$\pi$での状態価値が求まることになります！
証明は一応できるみたいです

前提条件

さて，順番が入れ替わってしまいましたが，このやり方（これこそが動的計画法なのですが）で解けるのは，環境のモデルが完全に分かっているときのみです

なので，バックアップ（更新のために溜めておく）のは，1つ前の各状態になりますね
すべての状態を溜めておく必要があるので，完全バックアップと言われます

次回ででてくるモンテカルロはまた違うものをバックアップします

方策評価と方策改善

方策評価

さて，さきほどの式である状態における状態価値を計算できることがわかりました．
ここで大切なのは，方策$\pi$のもとで！ということです．

この，ある方策$\pi$のもとで，状態価値を計算することを方策評価といいます

アルゴリズムとしてはこんな感じ

1. すべての状態価値$V(s)$を0とする
2. 1回前の計算結果$V(s)$を用いて，更新
3. 更新量が小さいかチェック
   4. ちいさければ終了
   5. 大きければ，2に戻る

更新式は，次の通りです

\begin{align}
V_{k+1}(s) = \sum_a \pi(s, a) \sum_{s'} \rho_{ss'}^a [R_{ss'}^a + \gamma V_k(s') ]
\end{align}

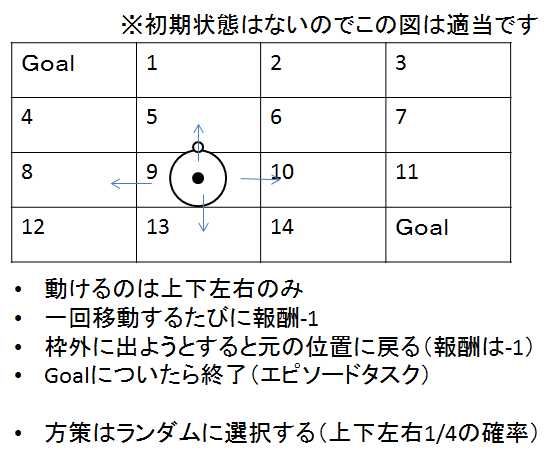
では，理解を深めるためにある迷路の問題をやってみます
問題はこんな感じ（教科書より引用）

つまり，上下左右に動ける人がいて，ランダムに動いた場合の方策評価をしてください
ゴールはの状態価値は0.0です
という問題です

モデルが分かっているので，今回はすべての状態価値を1つ前の状態価値で計算します

なのでアルゴリズムとしては，先ほども書いたように

1. 初期化
2. すべての状態で，1つ前の状態を更新
3. 繰り返し

更新に必要な変数はすべて求まっています

あとはこれをプログラムに書きおこすだけです
ちなみに，どの状態に移り変わっても報酬は-1なので（状態遷移にマイナスの報酬が入る設定です）
また，移動できるのは右左上下
よくプログラミング大会とかの考えと同じで地図は，行列で管理しましょう．

結果だけ

[[  0. -14. -20. -22.]
 [-14. -18. -20. -20.]
 [-20. -20. -18. -14.]
 [-22. -20. -14.   0.]]

こんな感じになります（教科書と同じです）
ゴールの状態は0になっており，ゴールから遠いところの価値が小さくなってますね
完璧です

プログラムはこんな感じ
2000回ぐらい繰り返すと収束します

import numpy as np
import matplotlib.pyplot as plt

# Dynamic Program
class Dynamic_program():
    def __init__(self, map_size): # map(numpy), goal(numpy), 
        self.map_size = map_size
        self.map_rows = self.map_size[0] # 行
        self.map_colums = self.map_size[1] # 列
        self.before_V = np.array([[0.0 for i in range(self.map_colums)] for j in range(self.map_rows)])

    def update(self, policy):
        # それぞれの行動分回す（状態遷移確率はない）
        New_V = np.array([[0.0 for i in range(self.map_colums)] for j in range(self.map_rows)])

        for i in range(self.map_rows):# 状態をすべて選ぶ イレギュラーですが行からで(これは全探索の意味)
            if i == 0: # 1行目の最終状態は除く
                colums_start = 1
                colums_end = self.map_colums
            elif i == self.map_rows -1: # 最終行の最終状態は除く
                colums_start = 0
                colums_end = self.map_colums -1 
            else: # これはいつもどおり
                colums_start = 0
                colums_end = self.map_colums

            for k in range(colums_start, colums_end):

                # 各状態において計算
                sum_eval = 0.0
                for action in policy.actions:
                    # 次に移る状態がきまる
                    next_state_row, next_state_colum = self.calc_next_state(i, k, policy.actions_move[action])# 行と列とアクション
                    
                    # 報酬計算
                    reward = self.decide_reward(next_state_row, next_state_colum)

                    # 評価を計算 
                    sum_eval += policy.actions_rate[action]*(reward + self.before_V[next_state_row, next_state_colum])

                # 計算した報酬を代入
                New_V[i, k] = sum_eval                             
        # 更新
        self.before_V = New_V

        return New_V 

    def decide_reward(self, next_state_row, next_state_colum): # 報酬計算
        # 報酬決定(今回はすべてに対して-1)
        reward = -1
        
        return reward

    def calc_next_state(self, i, k, action): # 状態遷移チェック　範囲外なら元に戻す
        next_state_row = i + action[0] # 行
        next_state_colum = k + action[1] # 列

        if next_state_colum > self.map_colums-1:
            next_state_colum = self.map_colums -1

        if next_state_colum < 0:
            next_state_colum = 0

        if next_state_row > self.map_rows -1:
            next_state_row = self.map_rows -1

        if next_state_row < 0:
            next_state_row = 0
        
        return next_state_row, next_state_colum

class Policy():# 方策定義
    def __init__(self):
        self.actions = ['up', 'down', 'right', 'left']
        # 方策の確率
        self.actions_rate = {}
        self.actions_rate['up'] = 0.25
        self.actions_rate['down'] = 0.25
        self.actions_rate['right'] = 0.25
        self.actions_rate['left'] = 0.25

        # 動作
        self.actions_move = {}
        self.actions_move['up'] = [-1, 0]
        self.actions_move['down'] = [1, 0]
        self.actions_move['right'] = [0, 1]
        self.actions_move['left'] = [0, -1]

def main():
    iterations = 2000
    policy = Policy()
    map_size = [4, 4]
    dynamic_program = Dynamic_program(map_size)

    for i in range(iterations):
        V_s = dynamic_program.update(policy)
        print(V_s)


if __name__ == '__main__':
    main()

方策改善

さて，この答えは，ランダム方策（ランダムに上下右左を選ぶ）における状態価値でした．

強化学習における目的は

価値を知って，その価値を最大化する方策を得ることでした

つまりこれでだけでは，ある方策の良さしか評価できないので困ってしまうわけですね

ここで方策改善という考えが出てきます

このランダム方策がどれだけ良いのかをしってその方策を改善したいなというわけ

ではそれをどうやって知るのか
それは行動価値関数をもちいてしることができます

行動価値関数は以下の式で表されます

\begin{align}
Q^\pi(s) &= E_\pi \bigl[R_t | s_t = s, a_t = a] \\
&= E_\pi \bigl[\sum_{k=0}^{\infty} \gamma r_{t+k+1}|s_t = s, a_t = a] \\
&= \sum_{s'} \rho_{ss'}^a \bigl[R_{ss'}^a + \gamma V^\pi (s') ] 
\end{align}

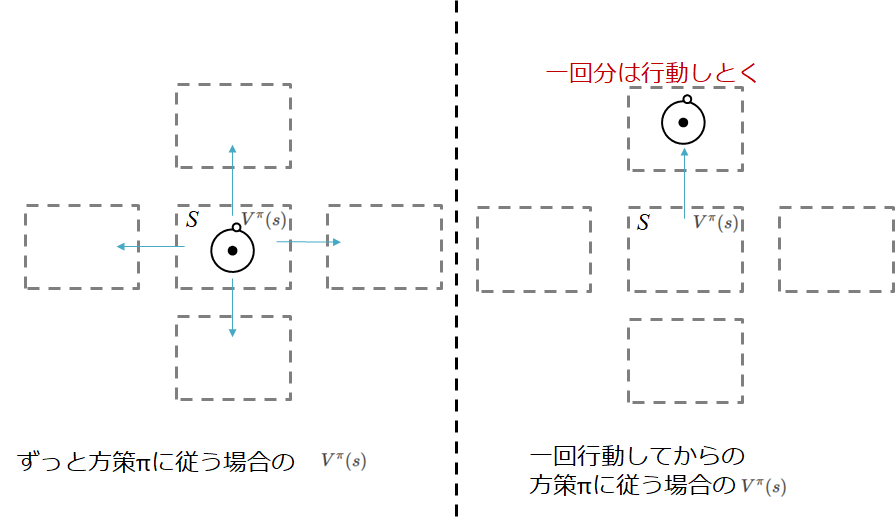
例えば，今ある状態$s$において行動$a$をとり，その後方策$\pi$に従った場合の状態価値が，状態$s$からずっと方策$\pi$にしたがった場合よりも大きければ．．．
行動を変えた方がいいことになります

図で表すとこんな感じ

この考え方？というかこれが成り立つことを方策改善定理といいます．
証明は本等にお預けします！が証明できます

そして，ここでgreedyという考えがでてきます

つまり，ある状態$s$において，その時にとれる最も高い報酬をもらえそうな行動を選択すれば，そのあとは最初から方策$\pi$によって行動するよりはいいだろってわけです．（すごく当たり前のことをいっています，方策$\pi$は確率ですからね，そりゃ最初の行動をもっともいいやつに確定させておけば高くなりますよね）

ちなみにこの考えは確率にも適用できます
つまり，その時にとれる最も高い報酬をもらえそうな行動に高い確率を振っておくということでも，この方策改善定理は成り立ちます
期待値が大きくなるので，なんとなくわかるかと思いますが．．．

よってこの方策改善定理に乗っ取れば方策を改善できるので，すべての状態において方策を改善すればよいわけです（上下右左，どれを選ぶか決めてしまう）
つまり

1. ある方策に乗っ取って状態価値関数を計算
2. 収束するまで計算
3. 収束したら，方策を改善（greedyに選ぶ）
4. 1に戻る

という方策改善と方策評価を繰り返し行っていくことによって，（方策反復といいます）
最適方策における最適な状態価値求めることができるのです

繰り返しの打ち切りは方策改善が終わるまでやります（変化しなくなるまで）

まだ続きます（長くなりますが．．．）

価値反復

さて，上記のやり方だと，上手くいきそうですが，いちいち方策評価をしなければならないという欠点があります
そんな計算待ってられないよ！！！怒
というわけです

そこで

収束性が証明されている手法に切り替えます（考え方は変わりません）

アルゴリズムはこうです

1. 方策評価を1ステップのみ行う（1回分）
2. 方策を改善する（一番いいやつ選ぶようにする）
3. 1に戻る

という作戦です．これを式で表すと

V_{k+1}(s) = \max_{a} \sum_{s'} \rho_{ss'}^a[r_{ss'}^a + \gamma V_k(s')] 

となります．
**どっかでみたことある！**ってなります
そうですこれ，ベルマン最適方程式を更新用に書き換えただけです

この式が表すのは，
最適方策（この場合はgreedy方策）のもとでの状態価値を求めていることになります
1回分しか計算しないのでこのように漸化式的に表せます！！

図でやるとこんな感じ（方策改善のところだけですが笑）

しかもこれ，最適方策の下で，最適状態価値に収束することが証明されています．

今回は以上なのですが，プログラミングしたら面白そうな問題がのってたのでやります

ギャンブラーの問題（教科書より引用しています）

問題としてはこうです
コインを投げるギャンブラーがいます
この人は，コインを投げて，表がでれば，自分が表にかけた金をすべてもらえますが，裏がでればすべてを失います
ゲームが終了するには

• 賭け金がなくなる（所持金が0になる）
• 目標の100ドルをもらって，カジノを退出

であり

ギャンブラーは1回のコイン投げでいくらをかけるのかきめなければならないという問題です

掛け金は整数とするので，

自分の状態はギャンブラーの所持金（1,2,3, ... 99）
行動はいくら賭けるか(1, 2, ... min(s, 100-s))　どっちか小さいほうなので（100ドルもらえばいいので，100ドルを結果的に超すような賭け金は設定しません）

コインの表が出る確率は0.4です

やってみましょう！！

価値反復を使います
さっきの迷路と同じように状態価値を全部0で初期化して．．．

選択するときはgreedyにします
すこしだけ注意というか考え方なのですが，今までは，前の状態価値$V_s$を用いて的な話をしてました．ただ，今回のプログラムは更新したら同じサイクルの中でもその更新した状態価値$V_s$を使ってます

これも，まとめて更新するのと，結局同じことをしてることになるはずなので（たぶん），まとめて計算しても最後は同じ値になるはずです．

import numpy as np
import matplotlib.pyplot as plt
import copy
import sys

class Gamble():
    def __init__(self):
        # 状態価値関数
        self.V_s = [0.0 for i in range(101)] # 状態は99個 + 最後の状態と最初の状態を追加
        self.V_s[-1] = 1.0 # 最後は報酬+1
        # 各状態でいくら賭けるか（policy）
        self.policy = [0 for i in range(101)]# 状態は99個 + 最後の状態と最初の状態を追加
        self.coin_rate = 0.4
        self.delta_limit = 1e-5 # 変更量閾値

    def update_V(self):
        delta = 1.0
        while delta >= self.delta_limit:
            delta = 0.0
            for s in range(1, 100):# すべての状態でやる これで1から99まで
                E = 0.0
                
                for i in range(1, min(s, 100-s) + 1):
                    # 期待値計算
                    temp_E = self.coin_rate * self.V_s[s + i] + (1.0 - self.coin_rate) * self.V_s[s - i]

                    # もっとも大きいものを選ぶ
                    E = max(temp_E, E)

                # 大きい方に合わせる
                delta = max(delta, abs(self.V_s[s]-E))
            
                # 更新
                self.V_s[s] = E
            
            # print(self.V_s)
        
        return self.V_s

    def calc_optimal_policy(self):
        # どれがいいか探します（すべての組み合わせをみて報酬が最大になった行動を返す）
        E = 0.0
        for s in range(1, 100):
            for i in range(1, min(s, 100-s) + 1): # 
                # 期待値計算
                temp_E = self.coin_rate * self.V_s[s + i] + (1.0 - self.coin_rate) * self.V_s[s - i]
                
                if temp_E > E + self.delta_limit:
                    E = temp_E 
                    self.policy[s] = i             

        return self.policy

    def plot(self, axis1, axis2):
        axis1.plot(range(1, 100), self.V_s[1:100]) # 状態価値
        axis2.plot(range(1, 100), self.policy[1:100]) # 最適方策

def main():
    coin = Gamble()

    count = 0

    V_s = coin.update_V()

    # 最適方策を計算
    opt_poliy = coin.calc_optimal_policy()

    figure = plt.figure()
    axis1 = figure.add_subplot(211)
    axis2 = figure.add_subplot(212)
    
    coin.plot(axis1, axis2)

    plt.show()

if __name__ == '__main__':
    main()

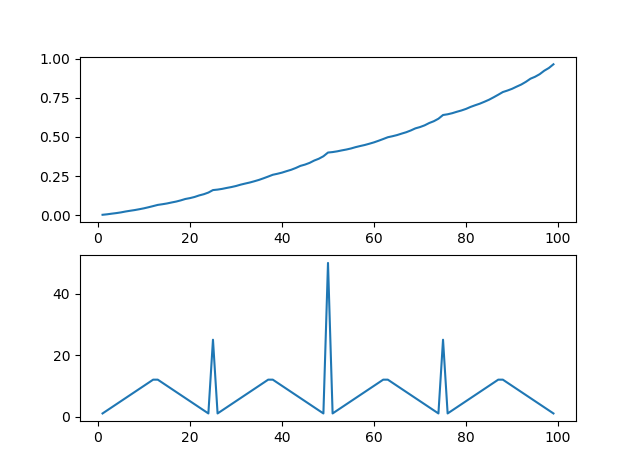
上が最適の状態価値
下が最適方策です

特徴的な形になりましたね
最適方策がすごく変な形をしてます
50において，すべての金をかけるのが良いのは，それがもっとも確率が高くなるからです．（50もってて，50もらえる可能性があるので）この問題は，かければかけるほどじり貧になります（0.4という確率から）

なので，勝負に出れるときは勝負に出た方がいいんです
50の時は特に顕著にそれが出ている感じです

なお最適方策を求めるときに，このように，マージンを持たせているのは，計算誤差があるからです．

if temp_E > E + self.delta_limit:
    E = temp_E
    self.policy[s] = i

こうしないときれいに形でないかもです
（確か公式のプログラムもうまくいかないはず）

次回はモンテカルロります

逐一更新とまとめて更新でも同じになることの証明

さっきの逐一更新の話ですが
プログラム上で確認したら一応同じになりました

ただし，逐一更新する場合は11回で収束
まとめて更新は17回で収束したので収束スピードが変わりそうです
なんとなく予想通り？

まとめて更新の場合のプログラム

import numpy as np
import matplotlib.pyplot as plt
import copy
import sys

class Gamble():
    def __init__(self):
        # 状態価値関数
        self.V_s = [0.0 for i in range(101)] # 状態は99個 + 最後の状態と最初の状態を追加
        self.V_s[-1] = 1.0 # 最後は報酬+1
        self.old_V_s = [0.0 for i in range(101)] # 状態は99個 + 最後の状態と最初の状態を追加
        self.old_V_s[-1] = 1.0 # 最後は報酬+1
        # 各状態でいくら賭けるか（policy）
        self.policy = [0 for i in range(101)]# 状態は99個 + 最後の状態と最初の状態を追加
        self.coin_rate = 0.4
        self.delta_limit = 1e-5 # 変更量閾値

    def update_V(self):
        delta = 1.0
        count = 0
        while delta >= self.delta_limit:
            count += 1
            delta = 0.0
            for s in range(1, 100):# すべての状態でやる これで1から99まで
                E = 0.0
                
                for i in range(1, min(s, 100-s) + 1):
                    # 期待値計算
                    temp_E = self.coin_rate * self.old_V_s[s + i] + (1.0 - self.coin_rate) * self.old_V_s[s - i]

                    # もっとも大きいものを選ぶ
                    E = max(temp_E, E)

                # 大きい方に合わせる
                delta = max(delta, abs(self.old_V_s[s]-E))
            
                # 更新
                self.V_s[s] = E
            
            self.old_V_s = copy.deepcopy(self.V_s)
            # print(self.V_s)

        print(count)
        
        return self.V_s

    def calc_optimal_policy(self):
        # どれがいいか探します（すべての組み合わせをみて報酬が最大になった行動を返す）
        E = 0.0
        for s in range(1, 100):
            for i in range(1, min(s, 100-s) + 1): # 
                # 期待値計算
                temp_E = self.coin_rate * self.V_s[s + i] + (1.0 - self.coin_rate) * self.V_s[s - i]
                
                if temp_E > E + self.delta_limit:
                    E = temp_E 
                    self.policy[s] = i             

        return self.policy

    def plot(self, axis1, axis2):
        axis1.plot(range(1, 100), self.V_s[1:100]) # 状態価値
        axis2.plot(range(1, 100), self.policy[1:100]) # 最適方策

def main():
    coin = Gamble()

    count = 0

    V_s = coin.update_V()

    # 最適方策を計算
    opt_poliy = coin.calc_optimal_policy()

    figure = plt.figure()
    axis1 = figure.add_subplot(211)
    axis2 = figure.add_subplot(212)
    
    coin.plot(axis1, axis2)

    plt.show()

if __name__ == '__main__':
    main()