はじめに
強化学習勉強会なるものがスタートしました!
なので,それらを勉強もかねてまとめていこうと思います.二番煎じ感がものすごいですが,自分の理解度向上のためにも!
予定ではQiitaで第7回分(Q学習ぐらいまで)ぐらいやろうかなと考えています.今回は第三回です!
過去のもの
- 第一回:概要
- 第二回:n本腕バンディット
- 第三回:用語まとめ編
- 第四回:動的計画法
- 第五回(1):モンテカルロ法(ES法)
- 第五回(2):モンテカルロ法(方策ON型,方策OFF型)
- 第六回(1):TD学習(ランダムウォーク)
- 第六回(2):TD学習(Q学習・Sarsa学習)
その他リンク
- github
https://github.com/Shunichi09/ - twitter
https://twitter.com/ShunichiSekigu1?lang=ja - 参考書
http://www.morikita.co.jp/books/book/1990 - 参考書(原本)
http://incompleteideas.net/book/bookdraft2018jan1.pdf - 原著プログラム
https://github.com/ShangtongZhang
原著プログラムについてですが,基本的には見ずに書いてます.
原著のプログラムが分かりにくければ,僕のgithubで見ていただけると嬉しいです.
目的
- 強化学習勉強会の内容のまとめ
- 自分の理解度向上もかねて
- プログラムの書き方の練習もかねて
おしながき
- 強化学習って結局?
- 用語再び
- 今回は理論編なので...
強化学習って結局?
前回、N本腕バンディット問題(良い腕を選ぶってだけですが)を解きました
結局あれは、何をしているのでしょうか?
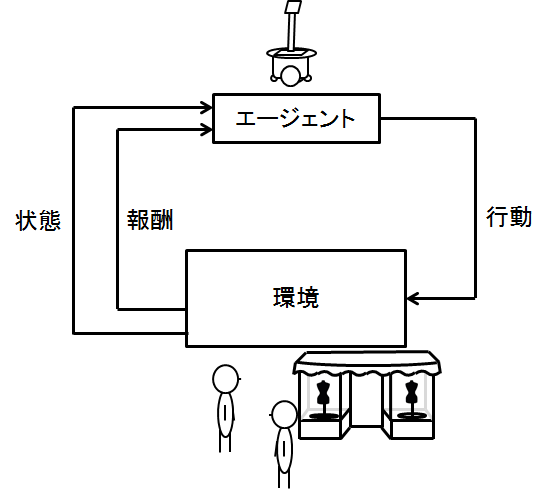
改めて復習も兼ねて以下の図をもう一度見てみましょう
これはよくある強化学習の図です
エージェントが行動し,環境がそれに応じて,状態を変化させて,報酬をエージェントに返すわけです
ここでいう今後もらえる報酬の和を最大にしよう!というのが強化学習のモチベーションでした
つまりその和が価値になるわけです
価値(これから貰えるだろーなっていう報酬の和)が最大になるような行動を取っているわけです
ということは
以下のことが強化学習にとって最も重要になります
-
ある状態の価値を知ること
(方策ベースの話もありますがいまはこれだけで!)
これを知れれば、あとは価値の高い状態に移り変わるように行動すればきっとうまくいきます
ここから数学のお話
強化学習では基本的に,確率(期待値)で物事が進んでいきます
なので,残念ながらここからは今後のために出てくる言葉の意味の説明と定式化をしていかなければなりません
しかし!しかしではないかもしれませんが笑 そんなに難しくありません
ので,ゆっくりとみていただけたらと思います.
方策
これはある状態において,エージェント(ロボット)が行える行動の中から何を選ぶかの確率を表したものです
\pi_t(s, a)
この式はある時刻$t$においてロボットの状態が$s$の時,$a$を選ぶ確率となります.
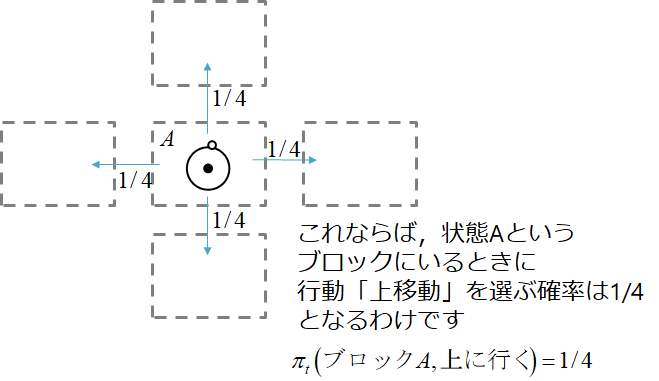
図で書くと下のイメージ
迷路でのイメージですね!
ちなみに添え字の$t$についてはガン無視してますが,これは時刻が関係する場合に考慮します(時間によって報酬が変わるなど)今は複雑になるので考慮してません
報酬
ある行動をとった結果もらえるご褒美的なものです.
r_t
で表されることが多く,これで,時刻$t$にもらった報酬になります
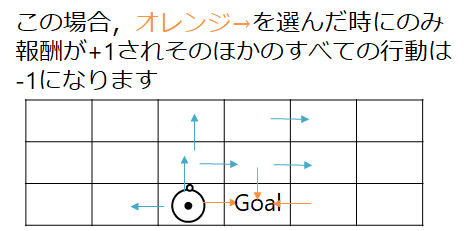
例えば,ある迷路に挑戦して,ゴールをもらった場合,+1
ゴールしない行動を選択しつづけた場合は-1とするみたいな例があります
水色⇒は省略してます
収益
ある時刻からみた,1つのゲームなど時刻の終わりまでプレーした際の報酬の合計になります.
単純に上の図の例なら,ゴールしたら1つのゲームが終わるので,ゴールするまでの報酬をすべて足し算すればよいわけですね
R_t = r_{t+1}+r_{t+2}+r_{t+3}+r_{t+4}+...r_{最終時刻}
これで,ある時刻$t$からみた収益になります(そのあとの時刻でもらえる報酬をすべて足せばよいわけです)
これを最大化できる方策をゲットすればなんとなく良いような気がします
割引率
上の収益の式だと,迷路ゲームのように終わりがなく,永久に続くものでは(振り子の制御など),収益が発散し,方策をうまく選択できなくなります.
なので,過去の報酬を割引することで,報酬や収益を収束させようという魂胆です
R_t = r_{t+1}+ \gamma r_{t+2}+ \gamma^2 r_{t+3}+ \gamma^3 r_{t+4}+...r_{最終時刻}=\sum_{k=0}^{\infty} \gamma r_{t+k+1}
もちろん割引率の$\gamma < 0$です.収束しなくなるので
ちなみに$\gamma = 0$とすれば,即時報酬(行動に対してもらえる報酬のみ意識する)ことになります
マルコフ性
でてきました
このマルコフさんです.音声認識などの時系列などを考える問題にもつきまとってきます
詳細は僕自身もあまり理解していないので,詳しいことを知りたい場合は,Google先生等にお願いします.
ただここで大事なのは
$t+1$における環境の応答は$t$における状態と行動にのみ依存すること
つまり
すべて,今時刻の行動にのみ依存するということです.
過去の行動は関係ありませんというと少し誤解があるかもしれませんが,
正確に言うなら,強化学習では$t+1$を$t$のみの情報で表現できるので問題を解くことができるんですね
ちなみにマルコフ性に従うタスクをマルコフ決定過程といい,状態が空間が離散の場合,有限マルコフ決定過程といいます
状態価値関数
さて,本回で最も大事なものが出てきました
この価値関数はある状態での価値を表した関数です.
つまり,その状態になるとどれくらい収益を今後もらえる可能性があるのかを定義したものということです.
実際の式を見てみましょう
V^\pi(s) = E_\pi \bigl[R_t | s_t = s] = E_\pi \bigl[\sum_{k=0}^{\infty} \gamma r_{t+k+1}|s_t = s]
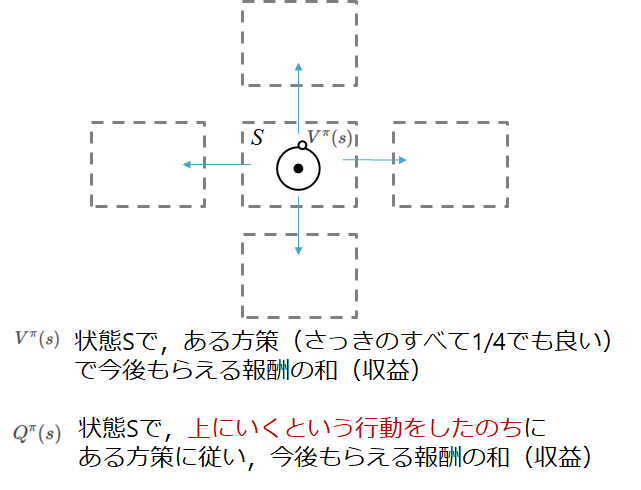
つまり,状態$s$にいて,方策$\pi$をとったときのどれだけ収益をもらえるか考えているわけです.
$E_\pi$は期待値を表します
行動価値関数
さきほどはある状態$s$にいて,方策$\pi$に従うとしたときのでした
なので次は
さきほどはある状態$s$にいて,行動$a$をとり,そのあとは,方策$\pi$に従った場合の行動価値関数を定式化します
Q^\pi(s) = E_\pi \bigl[R_t | s_t = s, a_t = a] = E_\pi \bigl[\sum_{k=0}^{\infty} \gamma r_{t+k+1}|s_t = s, a_t = a]
$a_t = a$という行動の条件が加わっているだけですね
つまり,状態価値関数の中で,ある時刻$t$の行動が指定されているイメージになります
上記2つをまとめるとこういう感じ
まとめているというか書いてるだけですが...
状態価値関数(再考)
さて,先ほどの式だとなんかよくわからないので再考しましょう
そもそも期待値ってどうやって処理するんですかという話なわけです
先ほどの式を見つめると
後半部分を以下のように考えることができます.
- ある状態でもらえる報酬の和(期待収益)
⇒ - ある状態で行動$a$をとってすぐにもらえる即時報酬+そのあとでもらえる期待収益
⇒ - ある状態で行動$a$をとってすぐにもらえる即時報酬+そのあと移り変わった状態でもらえる期待収益
つまり,今の状態$s$の価値関数は移り変わった状態($s'$)の価値関数で表現できることが分かります.
よって式はこんな風に変換できます
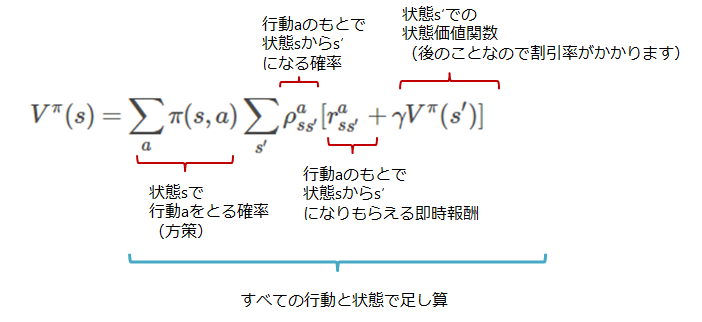
V^\pi(s) = \sum_{a} \pi(s, a) \sum_{s'} \rho_{ss'}^a[r_{ss'}^a + \gamma V^\pi(s')]
最適行動価値関数・最適状態価値関数
さきほどの式が理解できれば今回はおっけーなのかとおもいきや,最適行動価値関数というものも登場するので考えてみましょう.
最適状態価値関数は
V^*(s) = \max_{\pi} V^\pi(s)
ある状態で,状態価値関数を最大化する最適方策$\pi$を表しています
次に
最適行動価値関数は
Q^*(s, a) = \max_{\pi} Q^\pi(s, a)
これは,ある状態で行動$a$をとりそののちは行動価値関数を最大化する最適方策に従うことを表しています
はい
ちょっと複雑になってきましたが,要は,最適行動価値関数と最適状態価値関数を最大化するような最適方策$\pi$での話ですね.
これもさっきと同じように変換してみると
V^*(s) = \max_{a} \sum_{s'} \rho_{ss'}^a[r_{ss'}^a + \gamma V^*(s')]
よって,ある状態$s$での最適状態価値関数は,移り変わった状態の最適価値関数を用いて表現できることがわかります
これは,最適=最適+最適だという,ベルマンさんの最適性の原理に従っているやつです.
さて同じく最適行動価値関数も以下のように算出できます
Q^*(s, a) = \sum_{s'} \rho_{ss'}^a[r_{ss'}^a + \gamma \max_a' Q^*(s', a')]
さて,これが分かったからなにがいいんだよというわけなのですが
- 最適状態価値関数$V^*(s)$が分かっているということは,greedyな方策が最適方策になります
- 最適行動価値関数$Q^*(s, a)$が分かっているということは,単純に最適行動価値関数を最大化する行動$a$を行えばよいことになります
上についてですが,最適状態価値関数が分かっているのだから,次の状態の価値も分かります
なので,次の状態とその他もろもろを計算すればよくて,その計算結果がもっとも大きいものを選べばよいのです
なのでgreedy方策です
一方下についてですが,
もはやある行動$a$をとった場合の値が分かっているので,単純にどの行動をとればいいかはすぐにわかりますね
さらに言いますと
行動a'までもすぐにわかるので,もはやすべての行動を決定することができます
なんとなくゴールからさかのぼればよさそうなにおいがぷんぷんしますが,今回はここまで
この行動価値関数の詳しい説明は,モンテカルロ回で行いたいと思います
今回は理論編なので...
あんまりおもしろくはないと思います.
しかし,これが分かれば,次回の動的計画法,次々回のモンテカルロ法は理解できます.
次回更新までお待ちを!!(なんだかんだで理論はずっと説明しないといけないので続きますが...)
ブラックジャックとか迷路とかやろうかなと思います