はじめに
強化学習勉強会なるものがスタートしました!
なので,それらを勉強もかねてまとめていこうと思います.二番煎じ感がものすごいですが,自分の理解度向上のためにも!
予定ではQiitaで第7回分(Q学習ぐらいまで)ぐらいやろうかなと考えています.今回は第二回です!
過去のもの
- 第一回:概要
- 第二回:n本腕バンディット
- 第三回:用語まとめ編
- 第四回:動的計画法
- 第五回(1):モンテカルロ法(ES法)
- 第五回(2):モンテカルロ法(方策ON型,方策OFF型)
- 第六回(1):TD学習(ランダムウォーク)
- 第六回(2):TD学習(Q学習・Sarsa学習)
その他リンク
- github
https://github.com/Shunichi09/ - twitter
https://twitter.com/ShunichiSekigu1?lang=ja - 参考書
http://www.morikita.co.jp/books/book/1990 - 参考書(原本)
http://incompleteideas.net/book/bookdraft2018jan1.pdf - 原著プログラム
https://github.com/ShangtongZhang
原著プログラムについてですが,基本的には見ずに書いてます.
原著のプログラムが分かりにくければ,僕のgithubで見ていただけると嬉しいです.
目的
- 強化学習勉強会の内容のまとめ
- 自分の理解度向上もかねて
- プログラムの書き方の練習もかねて
おしながき
- n本腕バンディット問題
2. 問題設定
3. 問題の定式化
3. 強化学習への落とし込み
4. 難しさ(知識利用と探索)
4. プログラム
n本腕バンディット問題とは
聞こえだけだとなにやらとっても難しそうですが
やる問題としてはいたって簡単です
腕が何本かついているスロットを用意します
腕を引くとスロットが回って,いくらかの利益(報酬)がもらえます
どの腕を引けばよいでしょうか?それを学習してください
という問題です
問題の定式化と強化学習への落とし込み
問題の定式化を行います ここから数学の話がでてきますが,まだ簡単ですので大丈夫です(第四回ぐらいから急に来ます)
この問題で言う前回定義した強化学習の要素、エージェントとか環境とか報酬、価値は、以下の通りになります
エージェント
スロットマシンを引くロボット?というか引く人
行動
どの腕を引くか
(行動$a$)とします
環境
この問題においては特に考えなくて大丈夫です
状態
この問題においては特に考えなくて大丈夫です
腕を引くことで状態は変化しません
報酬
スロットマシンを引いたことで得られる利益です
今回は,報酬がガウス分布(正規分布です)で表されるとしています
よって,報酬の真値を$Q(a)$とした場合,実際に得られる報酬は分散1,平均$Q^{*}(a)$に従うものになりますね*
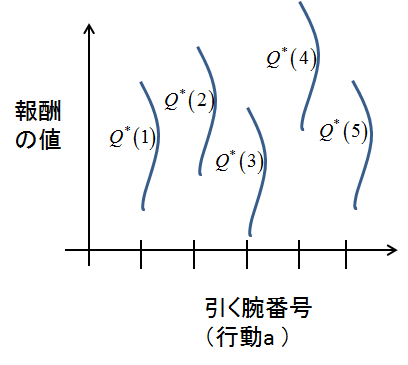
図のイメージ
この場合はスロットが5本の腕を持つとしています
価値
この問題においては推定される報酬になります
推定される報酬とは・・・
普通に考えたら何回か試してみてその平均をとりますよね
それで一番確率が高そうなやつを選ぶと思います
それです
それを標本化平均法といいます
数学チックに書くと
$t$番目のプレイで,ある行動$a$を$k$回とったときの価値の推定(この腕をひくことの価値)を
Q_t(a)=\frac{r_1 + r_2 + ... + r_k}{k}
と表します
t回プレーして(スロットの腕を引いた合計数)で,そのうちあるスロットを引いたのがk回だったら,k個分データがあるので,平均をとれば推定できそうです.
しかも行動する回数が増えれば増えるほど,真値に収束します(大数の法則ですね)
ちなみにプログラムに実装するときは
これだと目盛り食いすぎるので
$r_{k+1}$これをその時に得た報酬とすると
Q_{k+1} = Q_k + \frac{1}{k + 1} [r_{k+1}-Q_k]
で更新しましょう!
ちなみにこれはそんなに難しい式変換ではなく,要は更新分が平均にどう加算されるかをみているだけです
難しい点
さて,さっき平均をとって推定するといいました
あれ?何回試すの?本気でプレーするタイミングはいつになるの?
という疑問が湧いてきます
つまり
何回データをとって,何回本気でプレーするんですかというわけです.
さらに詳しくいいます
このゲーム,この腕きっと良いっていって引くんですけど
- ずっとこれがいいって思った腕を本気で引き続けて,確率が正しい値に収束しても,実は他のが高い場合がある
- かといってずっとあちこち浮気して引きまくってデータを集めてたら終わりが見えない
というわけです
ここで出てくるキーワードが貪欲法と,知識利用と探索になります
まず貪欲法です
これは,その名の通り,これだって思う腕を本気で引きまくる方法です
つまり,推定される価値が最も大きい腕を引き続けます
これは自分が知っている知識を利用し続けるので,知識利用になりますね!
しかし,これだけでは進化しません
なので,あるタイミングでデータを集めにいきます
これが探索になります!
この探索をランダムでやるのが,$\epsilon$-貪欲法になります!
大体10%ぐらいでデータ取りに行きます.その時の気分ですね
ただ,この手法,見た目普通なのに,かなり強力で,今でも使用されることもあります
人間っぽい学習方法だからかもしれませんね
再び問題設定
ではなんとなくできそうなので具体的にこの問題を解きます
ここで注意なのはスロットマシンも確率的なので,2000個のスロットマシンの真値は,平均0分散1のガウス分布から, 行動$a$の報酬の真値$Q*(a)$ を生成します.
なので!
- 行動選択によって得られる報酬も確率分布を利用
- そもそもの真値も確率分布を利用
になっていることにご注意ください
まず,確率を考えるので,このスロットマシンを2000個用意します笑
普通のパチンコ屋って何台あるのでしょうか笑
(教科書の問題設定なので許してください)
そして,それぞれのスロットの行動$a$に対する報酬を$Q^*(a)$とします
なので例えば,ある腕適当にを引くってなったら2000個おらって引きます
それで行動を推定していくというわけですね!
ここで注意点は,そのスロットマシンそれぞれで,引く腕は異なります
なのでここでいう行動aは,配列的になっています
マシン1では,腕1を引いて,マシン2では,腕4をひいて....ってなります
しかもそれぞれスロットマシンで貪欲か探索かを考えて
吟味するので,ここは勘違いしないようにしてください!!
プログラム
プログラム書きます
- 貪欲法
- $\epsilon$-貪欲法
を比較します
まず乱数生成(numpyの使います)
これは正規分布です!注意!
ちなみに補足ですが
90%の確率で選ぶとかをやりたいときは
1-10の数字で,その一様分布!で乱数発生させて,1-9でたら大きい方,10なら小さい方みたいに選ぶ作戦がいいかもです
参考です!
# bunpu.py
import numpy as np
import matplotlib.pyplot as plt
# グラフ作成
fig = plt.figure()
# axis
itiyo_ax = fig.add_subplot(131)
seiki_ax = fig.add_subplot(132)
coins_ax = fig.add_subplot(133)
figures = [itiyo_ax, seiki_ax, coins_ax]
# 一様分布(どれも等確率です)
y_1 = np.random.rand(1000)
# ヒストグラムを書きます
img = itiyo_ax.hist(y_1, bins=10, ec='black')
# 正規分布
y_2 = np.random.randn(1000)
# ヒストグラムを書きます
img = seiki_ax.hist(y_2, bins=20, ec='black')
# 10パーセントで裏,と90パーセントで表の出る確率
count_omote = 0
count_ura = 0
for i in range(1000):#1000回試行します
temp = np.random.randint(1, 11)
print(temp)
if temp > 9:
count_ura += 1
else:
count_omote += 1
print('Omote = {0}'.format(count_omote/1000))
print('Ura = {0}'.format(count_ura/1000))
img = coins_ax.bar([1, 0], [count_omote, count_ura], ec='black')
plt.tight_layout()
plt.show()
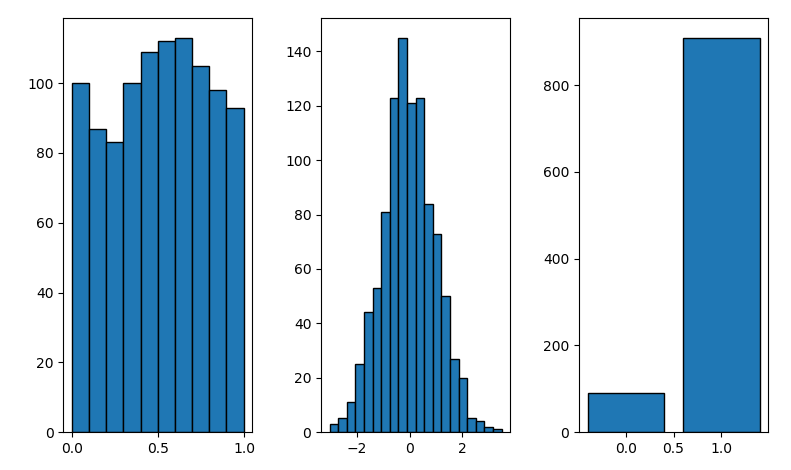
左から
- 一様分布
- 正規分布
- 90%で表が出るコインを1000回なげたときの結果
です
うまくいってますね!
では,いよいよプログラムです
numpyはrandomを使いましょう!
- まず,真値の報酬を作成します
- 続いて初期の報酬推定値をあたえます、今回は0にしてます
- どの腕を引くべきか考えます
- ゲームをやって、得られた報酬をもとに報酬推定値を更新します
# n_bandit.py
import sys
import numpy as np
import matplotlib.pyplot as plt
class Epsilon_greedy():
def __init__(self, rate):
self.random_rate = rate
self.greedy_rate = 1 - rate
class Greedy():
def __init__(self):
self.random_rate = 0
self.greedy_rate = 1
class Bandit():
def __init__(self, method_type, bandit_num, arms):
# パラメータ
self.method = method_type
self.arms = arms
self.bandit_num = bandit_num
# 各行動に対する報酬の真値
self.Q_true = np.random.randn(self.bandit_num, self.arms)
# 推定報酬
self.Q_esti = np.array([[0.0 for i in range(self.arms)] for j in range(self.bandit_num)])
self.Q_times = np.array([[0 for i in range(self.arms)] for j in range(self.bandit_num)]) # そのアームを何回引いたか
# 記録用
self.sum_rewards = []
def play(self):# 腕を引きます
a = self.decide_arm()
# 行動aが取られた場合の報酬
reward = []
for i in range(self.bandit_num):
reward.append(np.random.normal(self.Q_true[i, a[i]], 1))
sum_reward = sum(reward)/self.bandit_num
self.sum_rewards.append(sum_reward) # 報酬の記録
self.update_estimate(a, reward)
return self.sum_rewards
def decide_arm(self):# どの腕引くか決めます
a = []
# 貪欲か貪欲じゃないかの選択
for i in range(self.bandit_num):#各マシンで吟味します
temp = np.random.rand() * 10
# print(temp)
if temp > 10 * self.method.greedy_rate:
# 探索!(ランダムに選びます)
a.append(np.random.randint(0, 10))
else:
# 貪欲!
a.append(np.argmax(self.Q_esti[i]))
return a
def update_estimate(self, a, reward): # 推定値を更新します!
for i in range(self.bandit_num):
self.Q_times[i, a[i]] += 1
self.Q_esti[i, a[i]] = self.Q_esti[i, a[i]] + (1/self.Q_times[i, a[i]])*(reward[i] - self.Q_esti[i, a[i]])
if __name__ == '__main__':
greedy = Greedy()
epsilon_greedy_1 = Epsilon_greedy(0.01)
epsilon_greedy_2 = Epsilon_greedy(0.1)
game_1 = Bandit(greedy, 2000, 10)
game_2_1 = Bandit(epsilon_greedy_1, 2000, 10)
game_2_2 = Bandit(epsilon_greedy_2, 2000, 10)
playtimes = 1000
for i in range(playtimes):
rewards_1 = game_1.play()
rewards_2_1 = game_2_1.play()
rewards_2_2 = game_2_2.play()
plt.plot(range(1000), rewards_1, 'k', label='greedy')
plt.plot(range(1000), rewards_2_1, 'r', label='epsilon=0.01')
plt.plot(range(1000), rewards_2_2, 'b', label='epsilon=0.1')
plt.xlabel('play times')
plt.ylabel('reward')
plt.grid(True)
plt.show()
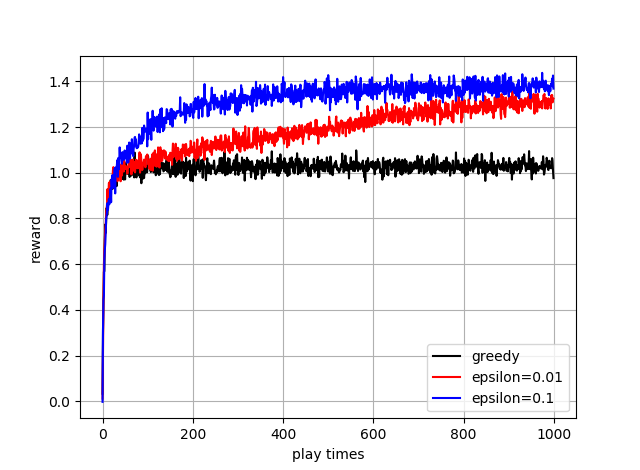
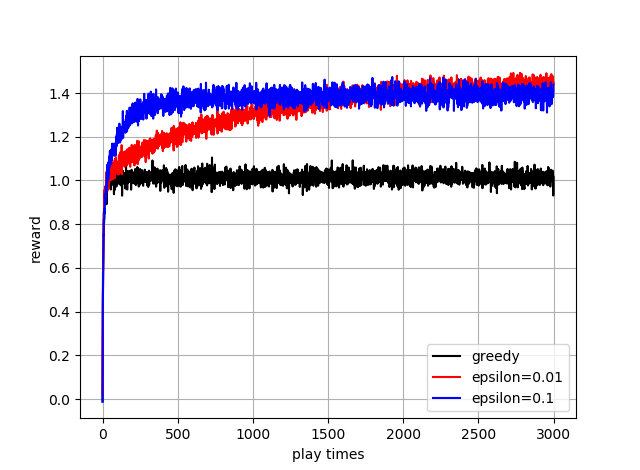
答えです!
教科書と同じですね!
表示してるのは,平均報酬です
つまりこれ,一定でランダムにした方がいいんです
ただ,これ回数ふやすと,イプシロンを小さくしたほうがゆくゆくは大きくなります
下図をみてみてください
ただ,この問題での理想値である,約1.55にはまだ遠いですね
ここでいろいろな工夫が考えられます
- イプシロンの値を変化させる
- 最初は大きくして,後から小さくするとか
- 初期推定を今は0にしてますが(プログラム参考),3とかにして,おけば,必ず一回はすべてを引くことになるので,greedyでも性能が上がるとか
ぜひトライしてみてください
しかもこんなことも考えられます
それは報酬が時間で変化することです
なので,そういう場合は直近の報酬が重くなるように更新します(加重平均)
この後教科書には
さまざまな手法が提案されていますが,そこまで本質的には重要でないので飛ばします
結論
イプシロングリーディー法をプログラムで書いてみました!
探索と知識利用のバランスがとっても重要ということです!
また,今回は行動によって状態は変化しませんでしたが,次回からは変化します!
次回は本格的に強化学習の式を書いていきます!