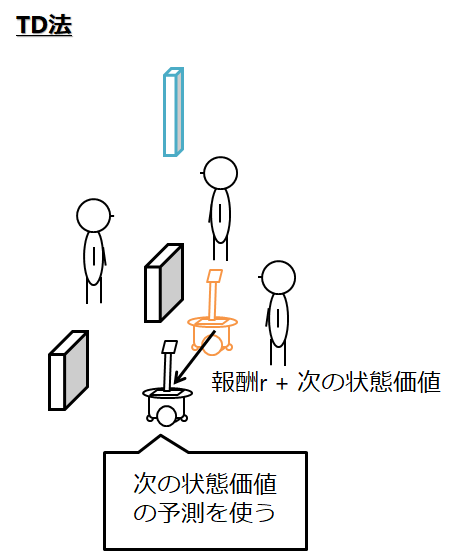
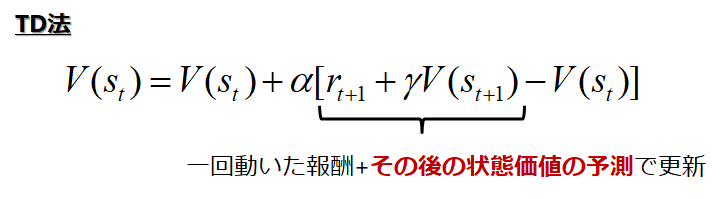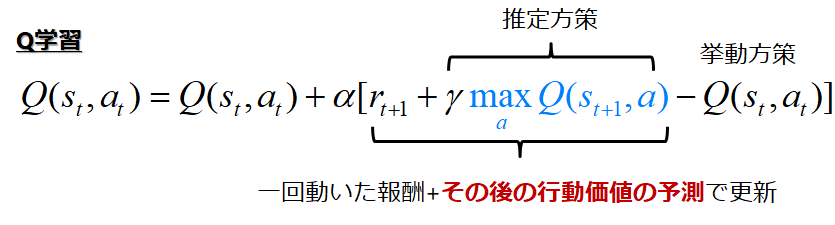はじめに
強化学習勉強会なるものがスタートしました!
なので,それらを勉強もかねてまとめていこうと思います.二番煎じ感がものすごいですが,自分の理解度向上のためにも!
予定ではQiitaで第7回分(Q学習ぐらいまで)ぐらいやろうかなと考えています.今回は第六回(1)です!
過去のもの
- 第一回:概要
- 第二回:n本腕バンディット
- 第三回:用語まとめ編
- 第四回:動的計画法
- 第五回(1):モンテカルロ法(ES法)
- 第五回(2):モンテカルロ法(方策ON型,方策OFF型)
- 第六回(1):TD学習の基本(ランダムウォーク)
- 第六回(2):TD学習(Q学習・Sarsa学習)
その他リンク
- github
https://github.com/Shunichi09/ - twitter
https://twitter.com/ShunichiSekigu1?lang=ja - 参考書
http://www.morikita.co.jp/books/book/1990 - 参考書(原本)
http://incompleteideas.net/book/bookdraft2018jan1.pdf - 原著プログラム
https://github.com/ShangtongZhang
原著プログラムについてですが,基本的には見ずに書いてます.
原著のプログラムが分かりにくければ,僕のgithubで見ていただけると嬉しいです.
目的と結論
目的
- Sarsa学習法とQ学習法,それぞれの理解と違いの理解
結論
- 風のある地図の学習
- 崖を歩く学習
から2つの違いが分かります.
おしながき
- Sarsa学習について
- Q学習について
- 風のある地を歩く(Sarsa学習)
- 崖を歩く(Sarsa学習 + Q学習)
Sarsa学習について
ここで価値関数で更新を行うのではなく,
行動価値関数で更新を行うとします.
これは本質的には何もかわりません
最適方策を見つけるためにモンテカルロ法で行ったときと同じです(正確に言うと,モデルがない場合は価値関数では実装できません,もちろん価値関数を求めるだけの場合は別ですが)
すると,,,
となります
ここでのQはε-greedyにすることが多いそうです
εでランダムの動きが起きるので.いろいろ経験できます
しかしここでポイントなのは
差分をとっているQ(推定方策)もε-greedyなんです
なので最終的にこのままではε-greedyでの行動価値関数になるわけです.
なのでεの値を時間に応じて小さくしていく
例えば,1/tにするといった対策をとることで,最終的には最適方策になります
ちなみにSarsaというのは,Q(s, a), r, Q(s, a)
の中身の頭文字をとって,Sarsaというわけです!
風のある地を歩く問題
では実装してみましょう
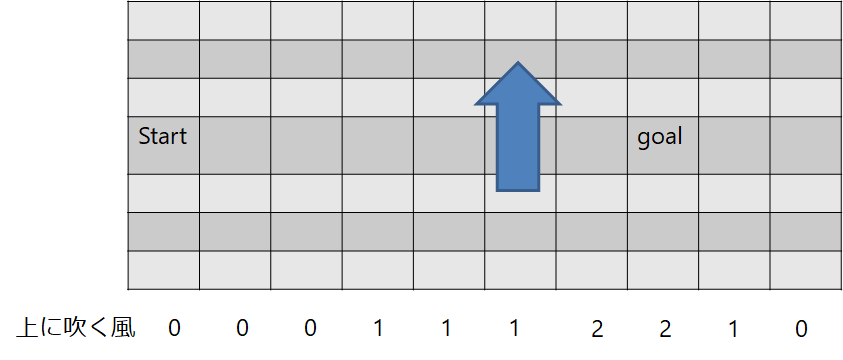
教科書の問題を参考にするとこんな問題です
start(3, 0)からgoal(3, 7)まで行くってことですね
行動は【”up”,”down”,”left”,"right"】
でも風があるので,...どうなるかというわけです
風のある地を歩く問題(結果)
学習の様子
(最初はなかなかゴールに辿りつけてませんがどんどんたどりつけるようになります)
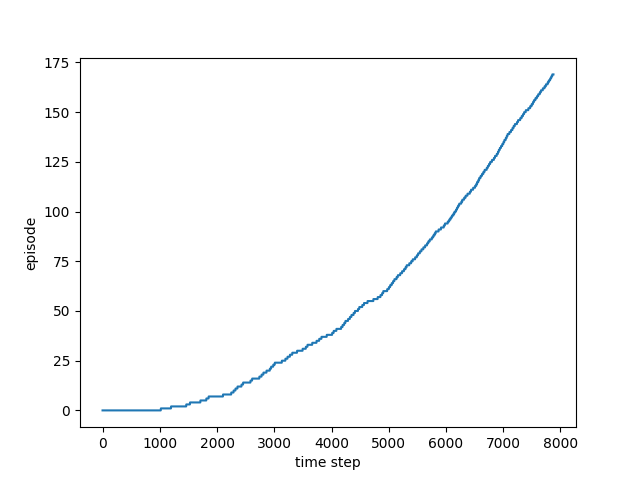
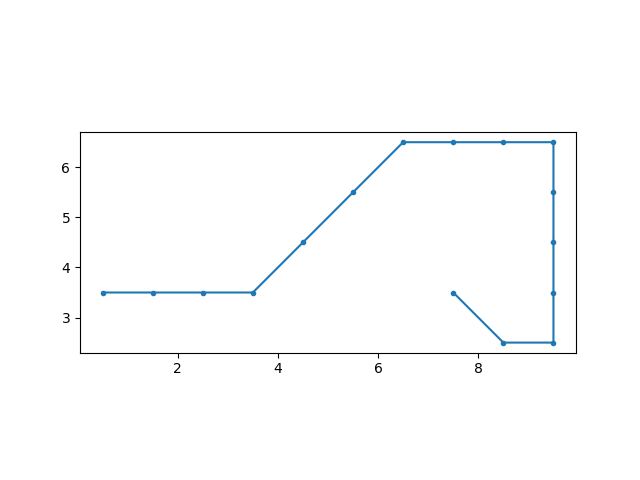
ε-greedy方策での行動価値関数での最適経路
学習できましたね!教科書と同じ結果です
直接的にはたどり着けないのでこうやって大回りして逆からアプローチしているわけです
ここでの考察としては,この問題はいつ終了するかわからないのでモンテカルロ法では学習が難しいです
でもTDであればこのように学習することができます
ちょっとだけ補足します
教科書では0.1にアルファが設定されていますが,それだと教科書より学習に時間がかかってしまいます
なので0.5に設定してください(原著のgithubはそうなってました)
あと,numpy等の実装を行う際に,argmaxは.一番初めの最大のインデックスを返してしまうので,最初の方の学習がうまく進みません
ここで,argmaxのインデックスが複数存在する場合は,その中からランダムに選ぶようにしましょう
コードは最後にのせておきます
Q学習について
さて,次にいよいよ登場しましたQ学習について説明していきます
Q学習は次の式で更新されます
ここで何が違うのかを考える必要があります
Q学習は更新するときに次の状態の最適方策で更新します
つまり!!推定している方策と,挙動している方策が異なります
なので最後は最適に落ちるわけです
ちなみに,推定方策と挙動方策の違いの,この話は方策OFF型でももでてきましたね!
なので,これはTDの方策OFF型というわけです
ちなみにお分かりのようにSarsaは方策ON型です
崖の近くを歩く
この違いが良く出る問題が教科書にのっていたのでやってみましょう
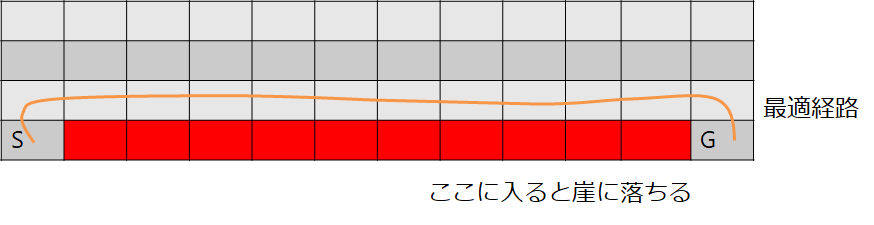
こういう問題です
最適経路は示したようになるのが正解ですね
崖の近くを歩く(結果)
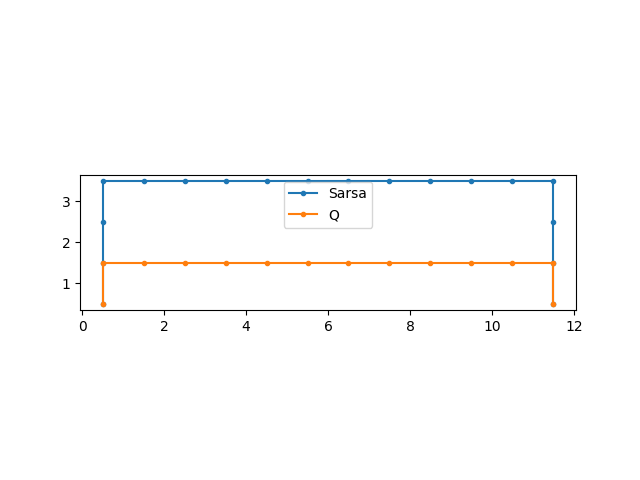
最適経路
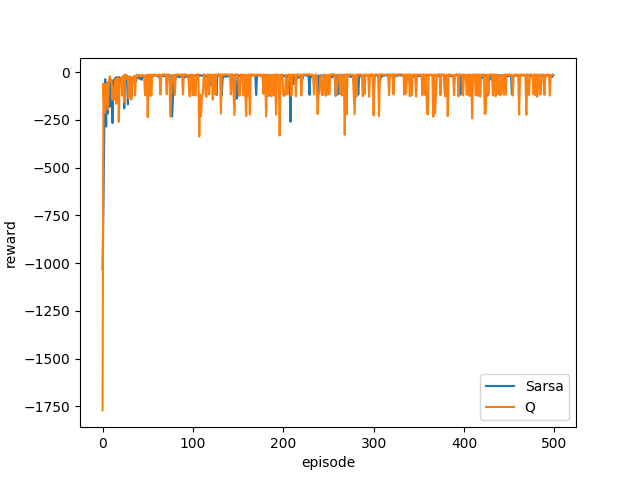
学習結果
(教科書の例は平滑化(何回かおなじ回数やって平均とってるっぽい)していますのでこの結果はふーん程度で大丈夫かと思います)
なんとなくQ学習のが報酬はすくなそう
結果をみるとSarsaは安全な道を選んでいるのに対して.
Qは,ぎりぎりを攻めています
この違いはなんでしょうか?
これはさっき言った,ε-greedyです
つまり,ε-greedyでの行動価値関数では,
崖付近でランダムに動く可能性が残っている(正確に言うと崖付近は価値が低くなる)ので,遠回りするんです
一方,Q学習については別です
最適方策を一生懸命学習します
しかし,学習しているときの報酬はSarsaの方がよいです
次がランダムに行動するのをふまえているからです
Qは自分が最適な推定方策なのに、挙動はε-greedyなので、崖の近くでランダムに動かれると落ちるわけですね
使い分けが難しそう
簡単なところまでのつもりでしたのでここまででQiitaにあげることは終わるつもりでしたが
せっかくなら、DQNとか、Policy Gradientとかのそのあたりの話もあげようとおもいます
教科書的にはまだ折り返しですし!
(原著だと折り返しでもない)
なのでまだまだ続きます!
例によってgithubにも上がってますが
風コード
import numpy as np
import matplotlib.pyplot as plt
import random
class WindField():
"""
environment wind map
Attributes
------------
map_row_size : int
row size of the map
map_colum_size : int
coulum size of the map
wind_map : numpy.ndarray
wind map
"""
def __init__(self):
self.map_colum_size = 10
self.map_row_size = 7
self.wind_map = np.zeros((self.map_row_size, self.map_colum_size))
# set the winds
for i, wind in enumerate([0, 0, 0, 1, 1, 1, 2, 2, 1, 0]):
self.wind_map[:, i] = wind
print(self.wind_map)
def state_update(self, state, action):
"""
state update with agent action
Parameters
------------
action : str
agent action the action must be chosen from ["right", "left", "down", "up"]
Returns
------------
next_state : numpy.ndarray
new position of agent
temp_reward : int
temporal reward result of agent action
end_flg : bool
flagment of goal
"""
next_state = np.zeros_like(state)
end_flg = False
if action == "left":
# row
next_state[0] = min(self.wind_map[state[0], state[1]] + state[0], self.map_row_size-1)
# colum
next_state[1] = max(state[1] - 1, 0)
elif action == "right":
# row
next_state[0] = min(self.wind_map[state[0], state[1]] + state[0], self.map_row_size-1)
# colum
next_state[1] = min(state[1] + 1, self.map_colum_size-1)
elif action == "up":
# row
next_state[0] = min(self.wind_map[state[0], state[1]] + state[0] + 1, self.map_row_size-1)
# colum
next_state[1] = state[1]
elif action == "down":
# row
temp = min(self.wind_map[state[0], state[1]] + state[0] - 1, self.map_row_size-1)
next_state[0] = max(temp, 0)
# colum
next_state[1] = state[1]
# judge the goal
if next_state[0] == 3 and next_state[1] == 7:
print("goal!")
temp_reward = 0.
end_flg = True
else:
temp_reward = -1.
return end_flg, next_state, temp_reward
class Agent():
"""
Agent model of reinforcement learning
Attributes
------------
state : str
now state of agent
states : list of str
state of environment
action_list : list of str
agent possibile action list
step rate : float
learning rate of reinforcement learning
discount rate : float
discount rate of reward
action_values : numpy.ndarray
avtion value function
"""
def __init__(self):
# environment
self.model = WindField()
self.state = None
self.action_list = np.array(["left", "right", "up", "down"])
self.step_rate = 0.5 # adjust subject
self.discount_rate = 1.0
# for bootstrap
self.history_state = None
self.action_values = np.zeros((self.model.map_row_size, self.model.map_colum_size, len(self.action_list))) # map size and each state have 4 action
def train_TD(self, max_train_num):
"""
training the agent by TD Sarsa
Parameters
-----------
max_train_num : int
training iteration num
"""
train_num = 0
history_episode = []
while (train_num<max_train_num):
# initial state
self.state = [3, 0]
end_flg = False
# play
action = self._decide_action(self.state)
while True: # if break the episode have finished
end_flg, next_state, temp_reward = self._play(self.state, action)
next_action = self._decide_action(next_state)
self._action_valuefunc_update(temp_reward, self.state, action, next_state, next_action)
# update the history
history_episode.append(train_num)
if end_flg:
break
# update
self.state = next_state
action = next_action
train_num += 1
return history_episode
def calc_opt_policy(self):
"""
calculationg optimized policy
Returns
---------
opt_policy : list of action
"""
# initial state
self.state = [3, 0]
end_flg = False
history_opt_policy = []
history_opt_state = []
while True: # if break the episode have finished
# play
action = self._decide_action(self.state, greedy_rate=0)
end_flg, next_state, temp_reward = self._play(self.state, action)
# save
history_opt_policy.append(action)
history_opt_state.append(self.state)
if end_flg:
break
# update
self.state = next_state
history_opt_state.append(next_state)
return history_opt_policy, np.array(history_opt_state)
def _play(self, state, action):
"""
playing the game
Parameters
-----------
state : str
state of the agent
action : str
action of agent
"""
end_flg, next_state, temp_reward = self.model.state_update(state, action)
return end_flg, next_state, temp_reward
def _decide_action(self, state, greedy_rate=0.1):
"""
Parameters
-----------
state : numpy.ndarray
now state of agent
greedy_rate : float
greedy_rate, default is 0.1
Returns
---------
action : str
action of agent
"""
choice = random.choice([i for i in range(10)])
if choice > (10 * greedy_rate - 1): # greedy, greedy rate is 0.1
action_value = self.action_values[state[0], state[1], :]
# this is the point
actions = self.action_list[np.where(action_value == np.max(action_value))] # max index
action = random.choice(actions)
else: # random
action = random.choice(self.action_list)
return action
def _action_valuefunc_update(self, reward, state, action, next_state, next_action):
"""
Parameters
-----------
reward : int
reward the agent got
state : str
now state of agent
action : str
action of agent
next_state : str
next state of agent
next_action : str
next action of agent
"""
print("action : {0} next_action : {1} \n now state : {2} next_state : {3}".format(action, next_action, state, next_state))
# TD
self.action_values[state[0], state[1], list(self.action_list).index(action)] =\
self.action_values[state[0], state[1], list(self.action_list).index(action)] +\
self.step_rate *\
(reward + self.discount_rate * self.action_values[next_state[0], next_state[1], list(self.action_list).index(next_action)] -\
self.action_values[state[0], state[1], list(self.action_list).index(action)])
def main():
# training
agent = Agent()
history_episode = agent.train_TD(170)
fig1 = plt.figure()
axis1 = fig1.add_subplot(111)
axis1.plot(range(len(history_episode)), history_episode)
axis1.set_xlabel("time step")
axis1.set_ylabel("episode")
# calc opt path
history_opt_policy, history_opt_state = agent.calc_opt_policy()
print("opt policy is = {0}".format(history_opt_policy))
print("opt state is = {0}".format(history_opt_state))
fig2 = plt.figure()
axis2 = fig2.add_subplot(111)
axis2.plot(history_opt_state[:, 1]+0.5, history_opt_state[:, 0]+0.5, marker=".")
axis2.set_aspect('equal')
plt.show()
if __name__ == "__main__":
main()
崖コード
import numpy as np
import matplotlib.pyplot as plt
import random
class CliffField():
"""
environment Cliff field
Attributes
------------
map_row_size : int
row size of the map
map_colum_size : int
coulum size of the map
cliff_map : numpy.ndarray
cliff map
"""
def __init__(self):
self.map_colum_size = 12
self.map_row_size = 4
self.cliff_map = np.zeros((self.map_row_size, self.map_colum_size), dtype=bool)
for i in range(1, self.map_colum_size-1):
self.cliff_map[0, i] = True
print(self.cliff_map)
# a = input()
def state_update(self, state, action):
"""
state update with agent action
Parameters
------------
action : str
agent action the action must be chosen from ["right", "left", "down", "up"]
Returns
------------
next_state : numpy.ndarray
new position of agent
temp_reward : int
temporal reward result of agent action
end_flg : bool
flagment of goal
"""
next_state = np.zeros_like(state)
end_flg = False
cliff_flg = False
if action == "left":
# row
next_state[0] = state[0]
# colum
next_state[1] = max(state[1] - 1, 0)
elif action == "right":
# row
next_state[0] = state[0]
# colum
next_state[1] = min(state[1] + 1, self.map_colum_size-1)
elif action == "up":
# row
next_state[0] = min(state[0] + 1, self.map_row_size-1)
# colum
next_state[1] = state[1]
elif action == "down":
# row
next_state[0] = max(state[0] - 1, 0)
# colum
next_state[1] = state[1]
# judge the goal
if next_state[0] == 0 and next_state[1] == 11:
print("goal!")
temp_reward = 0.
end_flg = True
else:
temp_reward = -1.
# judge cliff
cliff_flg = self.cliff_map[next_state[0], next_state[1]]
if cliff_flg:
temp_reward = -100.
next_state = [0, 0] # back to start
return end_flg, next_state, temp_reward
class Agent():
"""
Agent model of reinforcement learning
Attributes
------------
state : str
now state of agent
states : list of str
state of environment
action_list : list of str
agent possibile action list
step rate : float
learning rate of reinforcement learning
discount rate : float
discount rate of reward
action_values : numpy.ndarray
avtion value function
"""
def __init__(self):
# environment
self.model = CliffField()
self.state = None
self.action_list = np.array(["left", "right", "up", "down"])
self.step_rate = 0.5 # adjust subject
self.discount_rate = 1.0
# for bootstrap
self.history_state = None
self.action_values = np.zeros((self.model.map_row_size, self.model.map_colum_size, len(self.action_list))) # map size and each state have 4 action
def train_sarsa(self, max_train_num):
"""
training the agent by TD Sarsa
Parameters
-----------
max_train_num : int
training iteration num
"""
train_num = 0
history_reward = []
while (train_num<max_train_num):
# initial state
self.state = [0, 0]
end_flg = False
rewards = 0.
# play
action = self._decide_action(self.state)
while True: # if break the episode have finished
end_flg, next_state, temp_reward = self._play(self.state, action)
next_action = self._decide_action(next_state)
self._action_valuefunc_update(temp_reward, self.state, action, next_state, next_action)
# update the history
rewards += temp_reward
if end_flg:
history_reward.append(rewards)
break
# update
self.state = next_state
action = next_action
train_num += 1
return history_reward
def train_Q(self, max_train_num):
"""
training the agent by Q
Parameters
-----------
max_train_num : int
training iteration num
"""
train_num = 0
history_reward = []
while (train_num<max_train_num):
# initial state
self.state = [0, 0]
end_flg = False
rewards = 0.
while True: # if break the episode have finished
# play
action = self._decide_action(self.state) # ε-greedy
end_flg, next_state, temp_reward = self._play(self.state, action)
# Q learning
next_action = self._decide_action(next_state, greedy_rate=0) # max policy, virtual action
self._action_valuefunc_update(temp_reward, self.state, action, next_state, next_action) # calc action value
# update the history
rewards += temp_reward
if end_flg:
history_reward.append(rewards)
break
# update actual
self.state = next_state # actual next state
train_num += 1
return history_reward
def calc_opt_policy(self):
"""
calculationg optimized policy
Returns
---------
opt_policy : list of action
"""
# initial state
self.state = [0, 0]
end_flg = False
history_opt_policy = []
history_opt_state = []
while True: # if break the episode have finished
# play
action = self._decide_action(self.state, greedy_rate=0)
end_flg, next_state, temp_reward = self._play(self.state, action)
# save
history_opt_policy.append(action)
history_opt_state.append(self.state)
if end_flg:
break
# update
self.state = next_state
history_opt_state.append(next_state)
return history_opt_policy, np.array(history_opt_state)
def _play(self, state, action):
"""
playing the game
Parameters
-----------
state : str
state of the agent
action : str
action of agent
"""
end_flg, next_state, temp_reward = self.model.state_update(state, action)
return end_flg, next_state, temp_reward
def _decide_action(self, state, greedy_rate=0.1):
"""
Parameters
-----------
state : numpy.ndarray
now state of agent
greedy_rate : float
greedy_rate, default is 0.1
Returns
---------
action : str
action of agent
"""
choice = random.choice([i for i in range(10)])
if choice > (10 * greedy_rate - 1): # greedy, greedy rate is 0.1
action_value = self.action_values[state[0], state[1], :]
# this is the point
actions = self.action_list[np.where(action_value == np.max(action_value))] # max index
action = random.choice(actions)
else: # random
action = random.choice(self.action_list)
return action
def _action_valuefunc_update(self, reward, state, action, next_state, next_action):
"""
Parameters
-----------
reward : int
reward the agent got
state : str
now state of agent
action : str
action of agent
next_state : str
next state of agent
next_action : str
next action of agent
"""
print("action : {0} next_action : {1} \n now state : {2} next_state : {3}".format(action, next_action, state, next_state))
# TD
self.action_values[state[0], state[1], list(self.action_list).index(action)] =\
self.action_values[state[0], state[1], list(self.action_list).index(action)] +\
self.step_rate *\
(reward + self.discount_rate * self.action_values[next_state[0], next_state[1], list(self.action_list).index(next_action)] -\
self.action_values[state[0], state[1], list(self.action_list).index(action)])
def main():
# training
agent_sarsa = Agent()
sarsa_history_reward = agent_sarsa.train_sarsa(500)
agent_Q = Agent()
Q_history_reward = agent_Q.train_Q(500)
fig1 = plt.figure()
axis1 = fig1.add_subplot(111)
axis1.plot(range(len(sarsa_history_reward)), sarsa_history_reward, label="Sarsa")
axis1.plot(range(len(Q_history_reward)), Q_history_reward, label="Q")
axis1.set_xlabel("episode")
axis1.set_ylabel("reward")
axis1.legend()
# calc opt path
fig2 = plt.figure()
axis2 = fig2.add_subplot(111)
axis2.set_aspect('equal')
sarsa_history_opt_policy, sarsa_history_opt_state = agent_sarsa.calc_opt_policy()
Q_history_opt_policy, Q_history_opt_state = agent_Q.calc_opt_policy()
print("Sarsa opt policy is = {0}".format(sarsa_history_opt_policy))
print("Sarsa opt state is = {0}".format(sarsa_history_opt_state))
print("Q opt policy is = {0}".format(Q_history_opt_policy))
print("Q opt state is = {0}".format(Q_history_opt_state))
axis2.plot(sarsa_history_opt_state[:, 1]+0.5, sarsa_history_opt_state[:, 0]+0.5, marker=".", label="Sarsa")
axis2.plot(Q_history_opt_state[:, 1]+0.5, Q_history_opt_state[:, 0]+0.5, marker=".", label="Q")
axis2.legend()
plt.show()
if __name__ == "__main__":
main()