はじめに
強化学習勉強会なるものがスタートしました!
なので,それらを勉強もかねてまとめていこうと思います.二番煎じ感がものすごいですが,自分の理解度向上のためにも!
予定ではQiitaで第7回分(Q学習ぐらいまで)ぐらいやろうかなと考えています.今回は第五回(2)です!
過去のもの
- 第一回:概要
- 第二回:n本腕バンディット
- 第三回:用語まとめ編
- 第四回:動的計画法
- 第五回(1):モンテカルロ法(ES法)
- 第五回(2):モンテカルロ法(方策ON型,方策OFF型)
- 第六回(1):TD学習(ランダムウォーク)
- 第六回(2):TD学習(Q学習・Sarsa学習)
その他リンク
- github
https://github.com/Shunichi09/ - twitter
https://twitter.com/ShunichiSekigu1?lang=ja - 参考書
http://www.morikita.co.jp/books/book/1990 - 参考書(原本)
http://incompleteideas.net/book/bookdraft2018jan1.pdf - 原著プログラム
https://github.com/ShangtongZhang
原著プログラムについてですが,基本的には見ずに書いてます.
原著のプログラムが分かりにくければ,僕のgithubで見ていただけると嬉しいです.
目的と結論
目的
- 強化学習勉強会の内容のまとめ
- 自分の理解度向上もかねて
- プログラムの書き方の練習もかねて
結論
- 本記事の最後にはモンテカルロ法によって学習した,ブラックジャックというゲームの学習結果がのっています!
- この記事を理解していただければ,他の単純化できるゲームにて適用が可能です!
おしながき
- 前回とのつながりから~モデルがない場合は?
- モンテカルロ法
3. ブラックジャックのプログラム
4. ブラックジャック攻略
前回とのつながりから~モデルがない場合は?
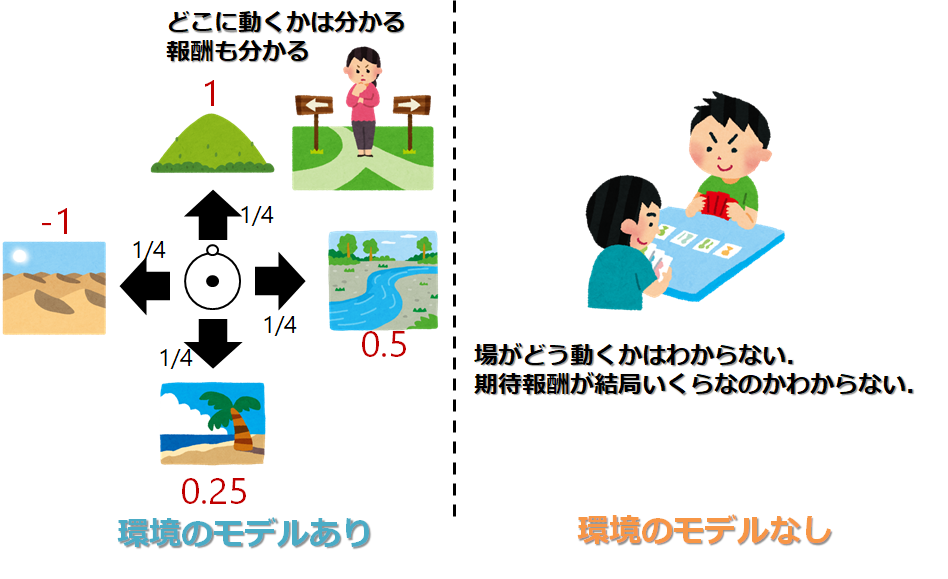
前回,第4回の動的計画法では,モデルが分かっている状態では話が進んでいました.
モデルがわかっているというのは,自分が行った行動に対して結果がどう出るか
つまり状態遷移確率が分かっていたということですね
右に動いたら右にいくのもそうです
ですが,分からないときもありますよね
そもそどんなゲームか分からない場合もそうです
行動を選択してどういう状態に移るのか
どんなゲームかわからないと出来ません
これをモデルが存在しないといいます
ただし!
今回はそういうものの中で、どういうゲームかは分かっているけど(モデルがあるけど),動的計画法だと厳しいものについて考えてみましょう
例えば!対戦型のカードゲーム、ブラックジャックを想定してみましょう
ルールはリンクをご覧ください
トランプを引き合うゲームなので
場がどう遷移するかは分かります
モデルはあるといえますが、、、
しかし、動的計画法は、遷移確率と、報酬の期待値を必要とします
プレイヤーがある状態でストップをかけた場合の報酬の計算、つまり実際に勝てるかどうかを計算するのは難しいです
例えば前回のギャンブラーの問題では、報酬ってすぐわかりますよね
100に行ってなかったらもうそれで0です
でも、今回はストップと言ってから、実際に勝ってるのかそれとも負けてるのかわかりません
(モデルがあるので計算することは可能です、しかし複雑です)
確率が分かっていればいいんでしょうけど
今回はそういう時にどうすべきか考えます
モンテカルロ法
場がどう動く、期待報酬が簡単には分からないときに使えるのがモンテカルロ法です
モンテカルロシミュレーションという言葉を聞いたことがあるかもしれませんが,多分それと同じです.
まんべんなく数うって平均とれば分かるでしょ戦法です
つまり、ある方策に則り、たくさんのケースを実際に体験して、そこからある方策のもとでの状態価値を求められませんかね?という作戦です
ここで、ある方策のもとでの状態価値の推定を方策評価というのでした
状態価値が分かれば方策改善ができそうです
前回の動的計画法とおなじ流れですね
アルゴリズム自体はさほど難しくありません
イメージした通りだと思います
以下流れです
- ある方策$\pi$の元でエピソードを作る
- エピソード上で体験した状態を保存しておく
- エピソードが終わり報酬等が確定した時点で,逆から計算して,状態の価値求める
- 1-3を繰り返し行い,各状態で平均をとる
です
1エピソードとは,1ゲームが終了することを意味します(ブラックジャックでいえば,勝ちか負けか確定するタイミング)
こうすれば,各状態でどれくらいの価値だったのかがわかります
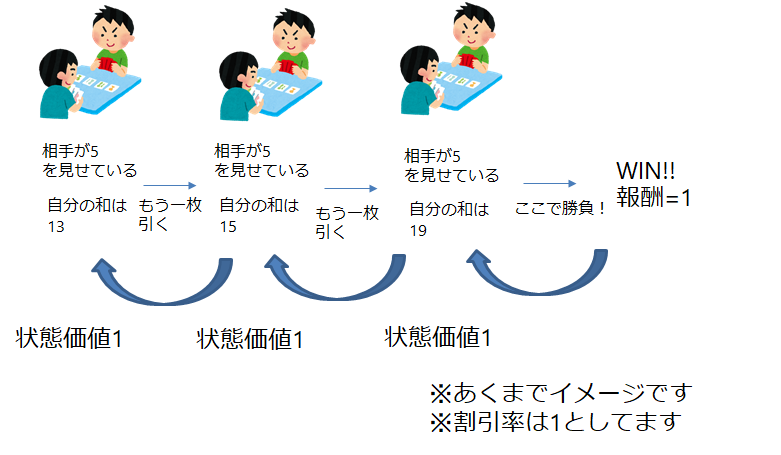
以下の図がイメージ
ブラックジャックを想定しています
逆から計算するのは,なんとなくわかると思います
最終のものが確定しないとわからないので
ではさっそくやってみましょう
ブラックジャックを想定します
ブラックジャックのルールは以下のものでした
(http://yamaimo.hatenablog.jp/entry/2015/10/01/200000)
ルールの概要
トランプを使用する。
トランプは無限デッキあると仮定する。(=カードの出る確率は変化しない)
Aは1もしくは11として扱う。
2〜10は数字通り扱う。
J, Q, Kは10として扱う。
カードの合計が21を越えず、出来るだけ21に近い方が勝ち。(同じなら引き分け)
プレイの流れ
ユーザーにカードが2枚オープンで配られる。
ディーラーにカードが1枚はオープン、もう1枚はクローズで配られる。
プレイヤーは以下の行動が出来る。
ヒット(カードをもう1枚引く)
スタンド(カードを引くのを止める)
カードの合計が21を越えたら、その時点でプレイヤーの負け。
スタンドするか21を越えるまでは、何度でもヒット出来る。
プレイヤーがスタンドを選択したら、ディーラーは伏せていたカードをオープンにし、カードの合計が17以上になるまでカードを引く。
カードの合計が21を越えたら、その時点でプレイヤーの勝ち。
ディーラーのカードの合計が21以下の場合、カードの合計を比べる。
カードの合計が21に近い方の勝ち。
同じなら引き分け。
さらに報酬は
- 勝ち1
- 負け-1
- 引き分け0
ここでいう状態は
- 相手が見せているカード(1-11)
- 自分の和(12-21)
- Aceを11としてつかっているか否か
の200個です
ちなみになんで自分の和12-21なんだよと思う方いると思いますが
12以上にならないとストップ(勝負)する意味ないんです
自分が11(Aceを持っていたら)だったらどうしますか?
どんだけ大きいカード引いても10です(キングとか絵札は10なので)
なので普通引きます
だから12-21の状態だけでいいんです
また,Aceの取扱についてですが,基本的には11で考えます
で21を超えるようであれば1として考えなおします
なぜかというと,1で考えておくことのメリットがないからです
例えば,自分が(4, Ace)を持っている時,15として考えるべきです
もし1として考えると5になって,引かないといけなくなります(12-21ですから)
他のケースについてもすべてそうです
なので最初は11と考えて,21を超えてはじめて,1として考えます
ここで
評価したい方策を
- 20以上でstop(勝負に出る)とします
ではさっきのイメージとアルゴリズムに乗っ取って,方策を評価してみましょう
200個の状態をすべてランダムではじめます
それから遊んでみて,報酬がでたら後はそれを蓄積して,平均とるだけです
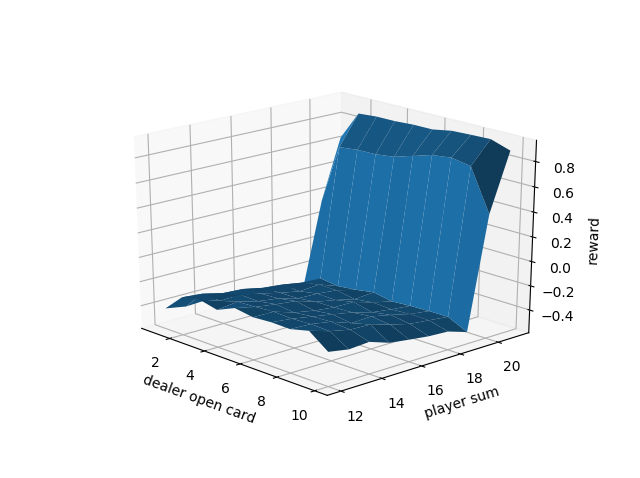
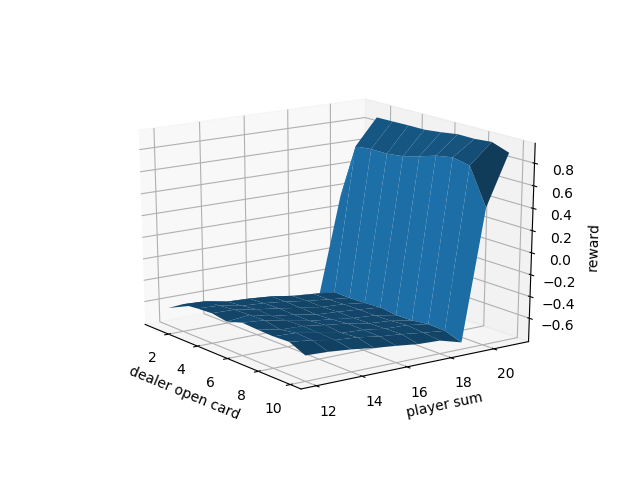
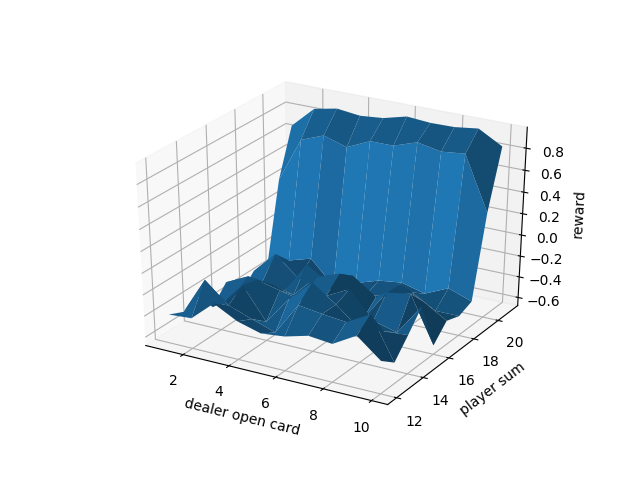
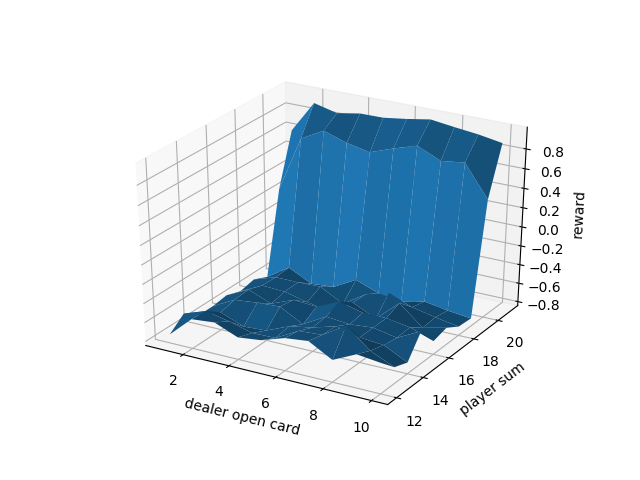
結果です(公式の結果と比較検証は行いましたたぶんあっています)
3Dplotについては[こちら](https://qiita.com/MENDY/items/e

5e14520201f82ef8a3c)をご覧ください
下が50万回プレーしてAceを11として使ってないとき
プログラム的にはdealerクラスとplayerクラスを作りそれで,実際にやってみてるだけです
難しいのは報酬のところかもしれません
そもそもこのゲーム,プレイヤーがくず手になった時点でプレイヤーの負け確定です
なので
def _reward(self, dealer_score, player_score): #価値計算
if player_score > 21: # dealerがくず手の時点で勝ち
reward = -1.0
else:
if dealer_score > 21: # 自分がくず手なら負け
reward = 1.0
else:
if player_score > dealer_score: # player勝ち
reward = 1.0
elif player_score < dealer_score: # dealer勝ち
reward = -1.0
elif player_score == dealer_score:
reward = 0.0 # 引き分け
return reward
としています
本当は,先に確定してreturnすべきなのですが,今回は,dealerもプレーしてから考えてます
# ブラックジャック
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import sys
def card_range_correcter(card): # 引いたカードはここ通す
if card > 10: # 絵札排除
card = 10
if card == 1: # とりあえずAceは11で計算
card = 11
return card
class Dealer(): # ディーラーの場合
def __init__(self):
# 見えているカード
self.open = card_range_correcter(np.random.randint(1, 11))
# ディラーが持っているカード(1枚が見えているカード)
self.cards = [self.open, card_range_correcter(np.random.randint(1, 14))]
def play(self): # ゲームする場合/交互に引くわけではないので,まずはディーラー
stop_flag, score = self._judge_stop()
while not stop_flag:
self._draw()
stop_flag, score = self._judge_stop()
return self.open, score # 開いてるカードの履歴と最終的なscoreを返す ディラーなのでこれだけでいい
def _judge_stop(self): # ゲーム終了かどうか判断(dealer)
# 初期化
stop_flag = False
# 和をとる
score = sum(self.cards)
# 大きさ確認
while 11 in self.cards and score > 21: # 21より大きくてAceを利用する場合
self.cards[self.cards.index(11)] = 1 # 1を代入
score = sum(self.cards)
# 17以上だとdealerはストップ
if score >= 17:
stop_flag = True
return stop_flag, score
def _draw(self): # カードを引く(dealer)
draw_card = card_range_correcter(np.random.randint(1, 14))
self.cards.append(draw_card)
class Player(): # playerの場合
def __init__(self):
# 持っているカードの和の推移(状態の推移)
self.player_sum_traj = [np.random.randint(12, 22)]
# Aceのtraj
self.Ace_flag_traj = [bool(np.random.choice([0, 1]))]
if self.Ace_flag_traj[0]:
self.cards = [self.player_sum_traj[0]-11, 11]
else:
temp = np.random.randint(2,10)
self.cards = [self.player_sum_traj[0]-temp, temp]
self.init_flag = True
def play(self):
stop_flag, score = self._judge_stop()
while not stop_flag:
self._draw()
stop_flag, score = self._judge_stop()
return self.player_sum_traj, self.Ace_flag_traj, score # 状態推移,Aceの推移,最終的なscore
def _judge_stop(self): # ゲーム終了かどうか判断(player)
# 初期化
stop_flag = False
# 和をとる
score = sum(self.cards)
if self.init_flag:
# print('player_sum_traj = {0}'.format(self.player_sum_traj))
# print('cards = {0}'.format(self.cards))
# 20以上だとplayerはストップ ここが方策になる
if score >= 20:
stop_flag = True
self.init_flag = False
else:
# 大きさ確認
while 11 in self.cards and score > 21: # 21より大きくてAceを利用する場合
self.cards[self.cards.index(11)] = 1 # 1を代入
score = sum(self.cards)
# 履歴に状態追加
self.player_sum_traj.append(score)
# print('player_sum_traj = {0}'.format(self.player_sum_traj))
# print('cards = {0}'.format(self.cards))
# 20以上だとplayerはストップ ここが方策になる
if score >= 20:
stop_flag = True
# ここでAceを利用しているか判定
if 11 in self.cards:
Ace_flag = True
else:
Ace_flag = False
# 履歴に追加しておく
self.Ace_flag_traj.append(Ace_flag)
return stop_flag, score
def _draw(self): # カードを引く(player)
draw_card = card_range_correcter(np.random.randint(1, 14))
self.cards.append(draw_card)
class Blackjack():
def __init__(self):
# モンテカルロのやつ保存する
# self.value_state = np.zeros((2, 10, 10))で三次元的にやるのもありですが...わかりにくそうなのでやめます
# 行がプレイヤーの和(12-21),列がディラーのopenカード(1-10)
self.value_state_Ace = np.array([[0.0 for i in range(10)] for k in range(10)])
self.value_state_No_Ace = np.array([[0.0 for i in range(10)] for k in range(10)]) # AceとAceなしでそれぞれ状態は10×10あります
# カウンター
self.count_value_state_Ace = np.array([[0 for i in range(10)] for k in range(10)])
self.count_value_state_No_Ace = np.array([[0 for i in range(10)] for k in range(10)]) # AceとAceなしでそれぞれ状態は10×10あります
def play(self):
# 各プレイヤー定義
self.dealer = Dealer()
self.player = Player()
# 次にプレイヤー
player_sum_traj, Ace_flag_traj, player_score = self.player.play()
# まずはディーラー
open_card, dealer_score = self.dealer.play()
# judge
reward = self._reward(dealer_score, player_score)
'''
print('player_sum_traj = {0}'.format(player_sum_traj))
print('opencards = {0}'.format(open_card))
print('delear_score = {0}'.format(dealer_score))
print('player_score = {0}'.format(player_score))
print('reward = {0}'.format(reward))
print('Ace_flag_traj = {0}'.format(Ace_flag_traj))
'''
# 初期訪問MCの場合 同じ状態の蓄積はいらない
player_sum_traj_unique = player_sum_traj
Ace_flag_traj_unique = Ace_flag_traj
''' 今回は同じ状態にならないのでいりません
for i in range(len(player_sum_traj)):
if player_sum_traj[i] not in player_sum_traj_unique:
player_sum_traj_unique.append(player_sum_traj[i])
Ace_flag_traj_unique.append(Ace_flag_traj[i])
'''
# print('player_sum_traj_unique = {0}'.format(player_sum_traj_unique))
# print('Ace_flag_traj_unique = {0}'.format(Ace_flag_traj_unique))
# 値補正
if open_card == 11: # 11換算でも見えているのはAce
open_card = 1
colums = open_card - 1
# 保存
for i in range(len(player_sum_traj_unique)):
if player_sum_traj_unique[i] > 21 or player_sum_traj_unique[i] < 12: # 22以上と11以下はいれてもしょうがないのでパス
continue
rows = player_sum_traj_unique[i] - 12
# print(player_sum_traj[i])
if Ace_flag_traj_unique[i]:
self.value_state_Ace[rows, colums] += reward
self.count_value_state_Ace[rows, colums] += 1
else:
self.value_state_No_Ace[rows, colums] += reward
self.count_value_state_No_Ace[rows, colums] += 1
# print('self.value_state_Ace = {0}'.format(self.value_state_Ace))
# print('self.value_state_No_Ace = {0}'.format(self.value_state_No_Ace))
return self.value_state_Ace, self.count_value_state_Ace, self.value_state_No_Ace, self.count_value_state_No_Ace
def _reward(self, dealer_score, player_score): #価値計算
if player_score > 21: # dealerがくず手の時点で勝ち
reward = -1.0
else:
if dealer_score > 21: # 自分がくず手なら負け
reward = 1.0
else:
if player_score > dealer_score: # player勝ち
reward = 1.0
elif player_score < dealer_score: # dealer勝ち
reward = -1.0
elif player_score == dealer_score:
reward = 0.0 # 引き分け
return reward
# 3Dgraphを作成
class Ploter_3D():
def __init__(self, x, y, z):
self.x = x # 1次元可能
self.y = y # 1次元可能
self. z = z # 2次元配列でほしい
# グラフ作成
self.fig = plt.figure()
self.axis = self.fig.add_subplot(111, projection='3d')
def plot_3d(self):
self.axis.set_xlabel('dealer open card')
self.axis.set_ylabel('player sum')
self.axis.set_zlabel('reward')
X, Y = np.meshgrid(self.x, self.y)
Z = self.z
self.axis.plot_surface(X, Y, Z)
plt.show()
def main():
game = Blackjack()
iterations = 500000
for i in range(iterations):
# print('i = {0}'.format(i))
value_state_Ace, count_value_state_Ace, value_state_No_Ace, count_value_state_No_Ace = game.play()
ave_value_state_Ace = value_state_Ace / count_value_state_Ace
ave_value_state_No_Ace = value_state_No_Ace / count_value_state_No_Ace
print(np.round(ave_value_state_Ace, 3))
print(np.round(ave_value_state_No_Ace, 3))
# 空配列が存在する場合⇒今回はないと想定
# 3Dplot
# 軸の作成
x = np.array(range(1, 11)) # sumの状態
y = np.array(range(12, 22)) # openされているカード
# 格子に乗る値
ploter_ace = Ploter_3D(x, y, np.array(ave_value_state_Ace))
ploter_ace.plot_3d()
ploter_No_ace = Ploter_3D(x, y, np.array(ave_value_state_No_Ace))
ploter_No_ace.plot_3d()
if __name__ == '__main__':
main()
さて,感想は圧倒的に不利ってことです笑
自分が-にいる状態が多いですね笑
これで,ある方策での方策評価を行うことができました
では,次にこの方策をどう改善していけばいいのでしょうか?
これを改善できれば,ブラックジャック攻略できます
ブラックジャック攻略!!モンテカルロES法
動的計画法では,
\begin{align}
Q^\pi(s) &= E_\pi \bigl[R_t | s_t = s, a_t = a] \\
&= E_\pi \bigl[\sum_{k=0}^{\infty} \gamma r_{t+k+1}|s_t = s, a_t = a] \\
&= \sum_{s'} \rho_{ss'}^a \bigl[R_{ss'}^a + \gamma V^\pi (s') ]
\end{align}
のように方策改善しましたが...
ここでいう状態遷移と報酬はわかりませんっていう話がさっきでてました
ただし,今回は行動価値がわかります.ようはどんな行動(ブラックジャックだと引く,ストップ)でもらえる収益(報酬の和)がわかりますよね
なので,単純に,一番いい行動価値になる行動を各状態でとればいいんです
\pi = arg\max_aQ(s, a)
?
ってなりそうですが,モンテカルロ法では,実際に体験している,状態と行動を対で保存することができます
なのでこの手法をとることができます
(動的計画法はどちらかというとエピソードを体験するというよりは,もともととける式の近似解法を行っているイメージです)
これのいいところは環境のモデルがいらないところです
状態遷移は考えてませんね とりあえずもらえる収益が高い行動を選ぶだけです
ちなみ行動価値は
さきほどはある状態$s$にいて,行動$a$をとり,そのあとは,方策$\pi$に従った場合の行動価値関数を定式化します
Q^\pi(s) = E_\pi \bigl[R_t | s_t = s, a_t = a] = E_\pi \bigl[\sum_{k=0}^{\infty} \gamma r_{t+k+1}|s_t = s, a_t = a]
>$a_t = a$という行動の条件が加わっているだけですね
>つまり,状態価値関数の中で,ある時刻$t$の行動が指定されているイメージになります
>上記2つをまとめるとこういう感じ
>まとめているというか書いてるだけですが...
>
ちなみに,これも,greedyに改善しているので,方策改善定理が使えます
一番いいやつ選んでるからなんとなく改善されそうです
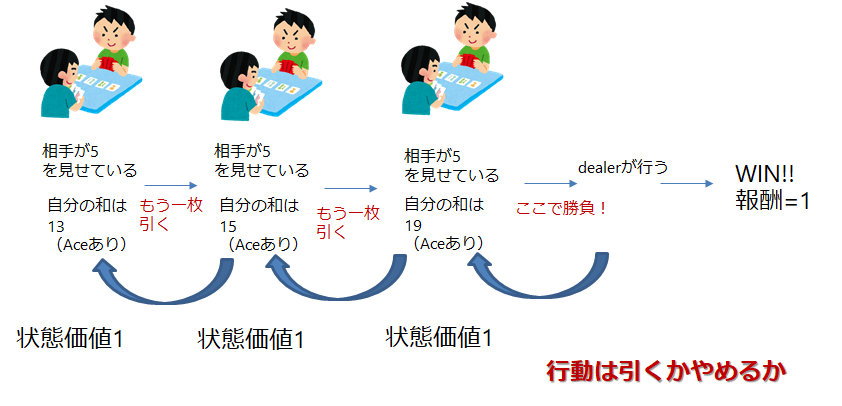
では,さっきのアルゴリズムの流れを少し変えてこの話を書いてみます
方策$\pi$を初期化
1. 方策$\pi$の元でエピソードを作る
2. エピソード上で体験した状態と行動のペア$(s,a)$を保存しておく
3. エピソードが終わり報酬等が確定した時点で,逆から計算して,行動価値$Q(s,a)$求める
4. 方策$\pi(s)$を行動価値$Q(s,a)$が大きくなるように改善する
4. 1-4を繰り返し行い,各状態で平均をとる
はい
変わったのは行動対の報酬を保存しているだけです
この手法をモンテカルロES法といいます
また前提として
- エピソードの開始をランダムな状態から始めること(すべての状態を観測したいので)
- 方策評価に無限のエピソードを行うことを仮定していることがあります
実際,上のアルゴリズムでは,方策評価のエピソードを無限に行わず(この考えは動的計画法と同じです),1エピソード毎に方策改善をしています
動的計画法では,証明されていましたが,このモンテカルロでは,形式的にはこのアルゴリズムでの最適方策への収束は証明されていないそうです
長くなりましたが,ここからこのアルゴリズムを用いて,ブラックジャック攻略法を見つけていきましょう!!!

とはいってもやることはあんまり変わりません
状態行動対を保存していくように書き換えるだけです
ただ注意点!
先程も言ったように、モンテカルロ法は、開始点探査を前提としています
最適方策で選び続けると、固定されたものしか選ばれないので、、、
なので、状態行動対はランダムにスタートさせます
さらに初期方策は、先程の20以上だとストップを採用します
またまた繰り返しになりますが、この初期方策とは、ランダムに選ばれた状態行動対の後に従うものなので!
流れとしては、
1. ランダムに状態行動対を作成
2. エピソードを始める
3. 最初の行動だけは、1で決めたものを使う
5. 次から方策に従う
6. 方策改善をする
これらを何百万回も繰り返す
です
結果はご覧の通り!
黄色がHIT!引く
緑色がStop!止まって勝負です!
これらは,100万回のエピソード後です
Aceを11として利用する場合

Aceを11として利用しない場合

まぁほぼ教科書と一緒です
(ちょっとplotの仕方がいまいち(ほんとは棒グラフ的なやつでやった方がいいと思います)なので,境目のところがうまくいってませんが)
ちゃんと中身をみると行けてそうですね!!

これによって!
ブラックジャックをやるときの戦術が学習できましたので,今度カジノに行く機会があったらやってみます
日本にもカジノができることですし,強化学習を用いてさまざまなゲームの攻略をどうにかできませんかね...
以下プログラムです
ちょっとごり押しで書いたのであんまりきれいじゃないです
まぁ今までのもきれいじゃないのであれですが,練習します!
第五回はここまでにします!
ただ,まだ補足があるので次回5-2回で説明します.
```py
# ブラックジャック
import numpy as np
# これで割り算を無し
# np.seterr(divide='ignore', invalid='ignore')
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import sys
def card_range_correcter(card): # 引いたカードはここ通す
if card > 10: # 絵札排除
card = 10
if card == 1: # とりあえずAceは11で計算
card = 11
return card
class Dealer(): # ディーラーの場合
def __init__(self):
# 見えているカード
self.open = card_range_correcter(np.random.randint(1, 11))
# ディラーが持っているカード(1枚が見えているカード)
self.cards = [self.open, card_range_correcter(np.random.randint(1, 14))]
def play(self): # ゲームする場合/交互に引くわけではないので,まずはディーラー
stop_flag, score = self._judge_stop()
while not stop_flag:
self._draw()
stop_flag, score = self._judge_stop()
return self.open, score # 開いてるカードの履歴と最終的なscoreを返す ディラーなのでこれだけでいい
def _judge_stop(self): # ゲーム終了かどうか判断(dealer)
# 初期化
stop_flag = False
# 和をとる
score = sum(self.cards)
# 大きさ確認
while 11 in self.cards and score > 21: # 21より大きくてAceを利用する場合
self.cards[self.cards.index(11)] = 1 # 1を代入
score = sum(self.cards)
# 17以上だとdealerはストップ
if score >= 17:
stop_flag = True
return stop_flag, score
def _draw(self): # カードを引く(dealer)
draw_card = card_range_correcter(np.random.randint(1, 14))
self.cards.append(draw_card)
class Policy():
def __init__(self):
# 行がプレイヤーの和(12-21),列がディラーのopenカード(1-10)
self.ace = np.array([['hit ' for i in range(10)] for k in range(10)])
self.no_ace = np.array([['hit ' for i in range(10)] for k in range(10)])
# 初期方策
self.ace[8:, :] = np.array([['stop' for i in range(10)] for k in range(2)])
self.no_ace[8:, :] = np.array([['stop' for i in range(10)] for k in range(2)])
def get_action(self, player_sum, Ace_flag, open_card): # opencardは補正済み
# 値修正
open_card = open_card - 1
player_sum = player_sum - 12
# print(open_card, player_sum)
if Ace_flag:
return self.ace[player_sum, open_card]
else:
return self.no_ace[player_sum, open_card]
def improve(self, player_sum_traj, Ace_traj, open_card, ave_Q_state_Ace, ave_Q_state_No_Ace):# 状態行動対をもらって方策を改善する
# print(ave_Q_state_Ace)
# print(ave_Q_state_No_Ace)
# open_card = open_card - 1
for i in range(len(player_sum_traj)):
if player_sum_traj[i] > 21 or player_sum_traj[i] < 12: # 22以上と11以下はいれてもしょうがないのでパス
continue
# 値修正
player_sum = player_sum_traj[i] - 12
# print('player_sum = {0}'.format(player_sum_traj[i]))
# print('open_card = {0}'.format(open_card))
if Ace_traj[i]:
# print('ave_Q_state_Ace[player_sum, open_card, 0] = {0}'.format(ave_Q_state_Ace[player_sum, open_card, 0]))
# print('ave_Q_state_Ace[player_sum, open_card, 1] = {0}'.format(ave_Q_state_Ace[player_sum, open_card, 1]))
if ave_Q_state_Ace[player_sum, open_card, 0] > ave_Q_state_Ace[player_sum, open_card, 1]:# hitの方が良い場合
self.ace[player_sum, open_card] = 'hit '
elif ave_Q_state_Ace[player_sum, open_card, 0] < ave_Q_state_Ace[player_sum, open_card, 1]:# standの方が良い場合
self.ace[player_sum, open_card] = 'stop'
else:
# print('ave_Q_state_No_Ace[player_sum, open_card, 0] = {0}'.format(ave_Q_state_No_Ace[player_sum, open_card, 0]))
# print('ave_Q_state_No_Ace[player_sum, open_card, 1] = {0}'.format(ave_Q_state_No_Ace[player_sum, open_card, 1]))
if ave_Q_state_No_Ace[player_sum, open_card, 0] > ave_Q_state_No_Ace[player_sum, open_card, 1]:# hitの方が良い場合
self.no_ace[player_sum, open_card] = 'hit '
elif ave_Q_state_No_Ace[player_sum, open_card, 0] < ave_Q_state_No_Ace[player_sum, open_card, 1]:# standの方が良い場合
self.no_ace[player_sum, open_card] = 'stop'
class Player(): # playerの場合
def __init__(self, policy):
# 持っているカードの和の推移(状態の推移)
self.player_sum_traj = [np.random.randint(12, 22)]
# Aceのtraj
self.Ace_flag_traj = [bool(np.random.choice([0, 1]))]
# Actionのtraj
self.action_traj = [np.random.choice(['hit ', 'stop'])]
# print(self.action_traj)
# 方策
self.policy = policy
if self.Ace_flag_traj[0]:
self.cards = [self.player_sum_traj[0]-11, 11]
else:
temp = np.random.randint(2,10)
self.cards = [self.player_sum_traj[0]-temp, temp]
self.init_flag = True
def play(self, open_card): # opencardは補正されてはいってくる
# dealerのカード
self.open_card = open_card
stop_flag, score = self._judge_stop()
while not stop_flag:
self._draw()
stop_flag, score = self._judge_stop()
return self.player_sum_traj, self.Ace_flag_traj, self.action_traj, score # 状態推移,Aceの推移,アクションの推移,最終的なscore
def _judge_stop(self): # ゲーム終了かどうか判断(player)
# 初期化
stop_flag = False
# 和をとる
score = sum(self.cards)
if self.init_flag:
# print('state_traj = {0}'.format(self.state_traj))
# print('cards = {0}'.format(self.cards))
# self.action_traj.append(self.policy.get_action(self.player_sum_traj[0], self.Ace_flag_traj[0], self.open_card))
# 方策にしたがう
if self.action_traj[0] == 'stop':
stop_flag = True
self.init_flag = False
else: # 初期状態ではない
# 大きさ確認
while 11 in self.cards and score > 21: # 21より大きくてAceを利用する場合
self.cards[self.cards.index(11)] = 1 # 1を代入
score = sum(self.cards)
# ここでAceを利用しているか判定
if 11 in self.cards:
Ace_flag = True
else:
Ace_flag = False
# print('state_traj = {0}'.format(self.player_sum_traj))
# print('cards = {0}'.format(self.cards))
if score > 21:
stop_flag = True
return stop_flag, score
# 履歴に追加しておく
self.Ace_flag_traj.append(Ace_flag)
# 履歴に状態追加
self.player_sum_traj.append(score)
# print(self.policy.get_action(self.player_sum_traj[-1], self.Ace_flag_traj[-1], self.open_card))
self.action_traj.append(self.policy.get_action(self.player_sum_traj[-1], self.Ace_flag_traj[-1], self.open_card))
# 方策にしたがう
if self.policy.get_action(self.player_sum_traj[-1], self.Ace_flag_traj[-1], self.open_card) == 'stop':
stop_flag = True
return stop_flag, score
def _draw(self): # カードを引く(player)
draw_card = card_range_correcter(np.random.randint(1, 14))
self.cards.append(draw_card)
class Blackjack():
def __init__(self):
# モンテカルロのやつ保存する
# self.value_state = np.zeros((2, 10, 10))で三次元的にやるのもありですが...わかりにくそうなのでやめます
# 行がプレイヤーの和(12-21),列がディラーのopenカード(1-10)
self.value_state_Ace = np.array([[0.0 for i in range(10)] for k in range(10)])
self.value_state_No_Ace = np.array([[0.0 for i in range(10)] for k in range(10)]) # AceとAceなしでそれぞれ状態は10×10あります
# カウンター
self.count_value_state_Ace = np.array([[0 for i in range(10)] for k in range(10)])
self.count_value_state_No_Ace = np.array([[0 for i in range(10)] for k in range(10)]) # AceとAceなしでそれぞれ状態は10×10あります
# 行動価値推定
self.Q_state_Ace = np.array([[[0.0, 0.0] for i in range(10)] for k in range(10)])
self.Q_state_No_Ace = np.array([[[0.0, 0.0] for i in range(10)] for k in range(10)]) # AceとAceなしでそれぞれ状態は10×10×2あります
# カウンター
self.count_Q_state_Ace = np.array([[[0, 0] for i in range(10)] for k in range(10)])
self.count_Q_state_No_Ace = np.array([[[0, 0] for i in range(10)] for k in range(10)]) # AceとAceなしでそれぞれ状態は10×10あります
# 行動価値推定(平均)
self.ave_Q_state_Ace = np.array([[[0.0, 0.0] for i in range(10)] for k in range(10)])
self.ave_Q_state_No_Ace = np.array([[[0.0, 0.0] for i in range(10)] for k in range(10)]) # AceとAceなしでそれぞれ状態は10×10×2あります
# 方策
self.policy = Policy()
def play(self):
# 各プレイヤー定義
self.dealer = Dealer()
self.player = Player(self.policy)
# まずはディーラー(あえて順番逆にしてます)
open_card, dealer_score = self.dealer.play()
# 補正
if open_card == 11: # 11換算でも見えているのはAce
open_card = 1
# 次にプレイヤー
player_sum_traj, Ace_flag_traj, action_traj, player_score = self.player.play(open_card)
# judge
reward = self._reward(dealer_score, player_score)
# print('player_sum_traj = {0}'.format(player_sum_traj))
# print('open_card = {0}'.format(open_card))
# print('delear_score = {0}'.format(dealer_score))
# print('player_score = {0}'.format(player_score))
# print('reward = {0}'.format(reward))
# print('Ace_flag_traj = {0}'.format(Ace_flag_traj))
# print('action_traj = {0}'.format(action_traj))
# 初期訪問MCの場合 同じ状態の蓄積はいらない
# 保存
open_card = open_card - 1
for i in range(len(player_sum_traj)):
if player_sum_traj[i] > 21 or player_sum_traj[i] < 12: # 22以上と11以下はいれてもしょうがないのでパス
continue
action = action_traj[i]
if action == 'hit ':
action = 0
else:
action = 1
player_sum = player_sum_traj[i] - 12
# print(state_traj[i])
if Ace_flag_traj[i]:
self.Q_state_Ace[player_sum, open_card, action] += reward
self.count_Q_state_Ace[player_sum, open_card, action] += 1
else:
self.Q_state_No_Ace[player_sum, open_card, action] += reward
self.count_Q_state_No_Ace[player_sum, open_card, action] += 1
# 平均出す
for i in range(len(player_sum_traj)):
if player_sum_traj[i] > 21 or player_sum_traj[i] < 12: # 22以上と11以下はいれてもしょうがないのでパス
continue
action = action_traj[i]
if action == 'hit ':
action = 0
else:
action = 1
player_sum = player_sum_traj[i] - 12
# print(state_traj[i])
if Ace_flag_traj[i]:
self.ave_Q_state_Ace[player_sum, open_card, action] = self.Q_state_Ace[player_sum, open_card, action] / self.count_Q_state_Ace[player_sum, open_card, action]
else:
self.ave_Q_state_No_Ace[player_sum, open_card, action] = self.Q_state_No_Ace[player_sum, open_card, action] / self.count_Q_state_No_Ace[player_sum, open_card, action]
# 方策改善
self.policy.improve(player_sum_traj, Ace_flag_traj, open_card, self.ave_Q_state_Ace, self.ave_Q_state_No_Ace)
return self.policy, self.Q_state_Ace, self.count_Q_state_Ace, self.Q_state_No_Ace \
, self.count_Q_state_No_Ace, self.ave_Q_state_Ace, self.ave_Q_state_No_Ace
def _reward(self, dealer_score, player_score): #価値計算
if player_score > 21: # dealerがくず手の時点で勝ち
reward = -1.0
else:
if dealer_score > 21: # 自分がくず手なら負け
reward = 1.0
else:
if player_score > dealer_score: # player勝ち
reward = 1.0
elif player_score < dealer_score: # dealer勝ち
reward = -1.0
elif player_score == dealer_score:
reward = 0.0 # 引き分け
return reward
# 3Dgraphを作成
class Ploter_3D():
def __init__(self, x, y, z):
self.x = x # 1次元可能
self.y = y # 1次元可能
self. z = z # 2次元配列でほしい
# グラフ作成
# self.fig_3D = plt.figure()
self.fig_2D = plt.figure()
# self.axis_3D = self.fig_3D.add_subplot(111, projection='3d')
self.axis_2D = self.fig_2D.add_subplot(111)
'''
def plot_3d(self):
self.axis_3D.set_xlabel('dealer open card')
self.axis_3D.set_ylabel('player sum')
self.axis_3D.set_zlabel('reward')
X, Y = np.meshgrid(self.x, self.y)
Z = self.z
self.axis_3D.plot_surface(X, Y, Z)
plt.show()
'''
def plot_hit_or_stop(self, title):
self.axis_2D.set_xlabel('dealer open card')
self.axis_2D.set_ylabel('player sum')
self.axis_2D.set_title(title)
X, Y = np.meshgrid(self.x, self.y)
Z = self.z
img = self.axis_2D.pcolormesh(X, Y, Z, cmap='summer')
pp=self.fig_2D.colorbar(img, orientation="vertical") # カラーバーの表示
pp.set_label('label') # カラーバーの表示
plt.show()
def main():
game = Blackjack()
iterations = 1000000
for i in range(iterations):
print('i = {0}'.format(i))
policy, Q_state_Ace, count_Q_state_Ace, Q_state_No_Ace, count_Q_state_No_Ace, ave_Q_state_Ace, ave_Q_state_No_Ace = game.play()
print('policy.ace = \n {0}'.format(policy.ace))
print('policy.no_ace = \n {0}'.format(policy.no_ace))
# 空配列が存在する場合⇒今回はないと想定
# 3Dplot
# 軸の作成
x = np.array(range(1, 11)) # sumの状態
y = np.array(range(12, 22)) # openされているカード
# 格子に乗る値
ploter_ace = Ploter_3D(x, y, np.array(policy.ace == 'hit ', dtype=int))
ploter_ace.plot_hit_or_stop('with_ace')
ploter_No_ace = Ploter_3D(x, y, np.array(policy.no_ace == 'hit ', dtype=int))
ploter_No_ace.plot_hit_or_stop('without_ace')
if __name__ == '__main__':
main()