はじめに
強化学習勉強会なるものがスタートしました!
なので,それらを勉強もかねてまとめていこうと思います.二番煎じ感がものすごいですが,自分の理解度向上のためにも!
予定ではQiitaで第7回分(Q学習ぐらいまで)ぐらいやろうかなと考えています.今回は第五回(2)です!
過去のもの
- 第一回:概要
- 第二回:n本腕バンディット
- 第三回:用語まとめ編
- 第四回:動的計画法
- 第五回(1):モンテカルロ法(ES法)
- 第五回(2):モンテカルロ法(方策ON型,方策OFF型)
- 第六回(1):TD学習(ランダムウォーク)
- 第六回(2):TD学習(Q学習・Sarsa学習)
その他リンク
- github
https://github.com/Shunichi09/ - twitter
https://twitter.com/ShunichiSekigu1?lang=ja - 参考書
http://www.morikita.co.jp/books/book/1990 - 参考書(原本)
http://incompleteideas.net/book/bookdraft2018jan1.pdf - 原著プログラム
https://github.com/ShangtongZhang
原著プログラムについてですが,基本的には見ずに書いてます.
原著のプログラムが分かりにくければ,僕のgithubで見ていただけると嬉しいです.
目的と結論
目的
- 強化学習勉強会の内容のまとめ
- 自分の理解度向上もかねて
- プログラムの書き方の練習もかねて
結論
- モンテカルロ法,方策ON型とOFF型によって,モンテカルロ法の弱点を補うことができる!
おしながき
- 前回とのつながりから~ランダム開始点と無限試行のお話し
- 方策ON型と方策OFF型
- GPIについて
前回とのつながりから~ランダム開始点のお話し
さらに、前回、第5回では、モデルがない場合、つまりどのような形で環境が推移するかわからない場合を考え、モンテカルロ法を使用し、行動価値関数を考えることで、ブラックジャックを攻略することができました.では、前回の問題の欠点について考えてみましょう.
それは,
開始点ランダム探査
無限個のエピソードを行える
という仮定です.
開始点ランダム探査はすべての状態を経験したいというモチベーションで行ってますが,最初のスタートが決まっていればすべての状態といつつ,意味のわからないポイントからスタートしてしまったり,さらにそこに時間依存のものが関わってくると(時間がたつとポイントが減るなど),開始点ランダム探査ですべての状態を体験しようというのは非現実的です.
さらに,2つ目の問題について,もし開始点探査がうまくいく問題だとしても,状態量が多い場合,すべての状態を経験することは計算時間を限りなく多くする必要があることになります.
なので,そこを改善します.
2つのアプローチ
- 方策ON型
- 方策OFF型
が存在します.
方策ON型がわかりやすいと思うので,そちらから説明します.
方策ON型
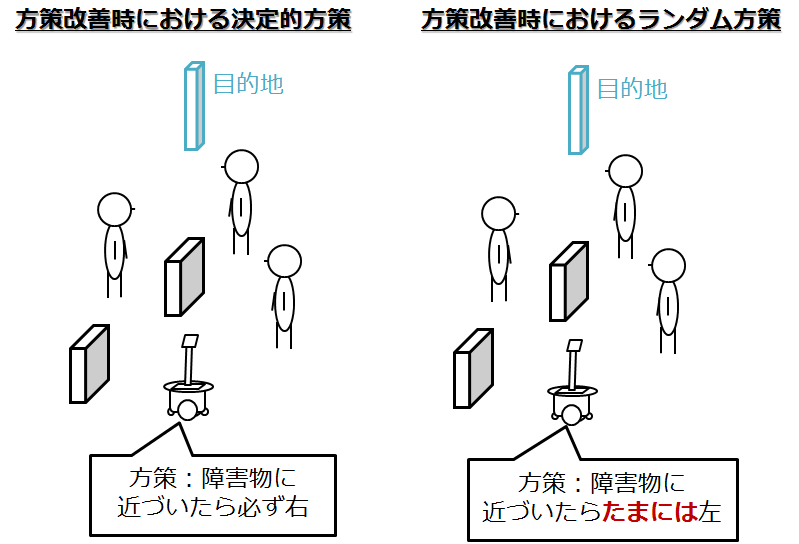
前回の方策評価,方策改善の流れは,常に決定論(確率が最大になるポイント)で選んでいました.つまり,決定論的試行⇒ランダム探査の組み合わせでしたね.
しかし,決定論で選んでいては,一回うまくいったやつを選び続けそうなことは容易に想像できます.
なので,決定論的に選んでいたところを改善し,いくらかの確率でランダムに選びます
これが,第二回で出てきた$\it{\epsilon-greedy}$法です.いくらかの確率でランダムで行動を選ぶ作戦です.これによってたまにランダムに選ぶので,すべての非greedyな行動に対してもある程度の確率を保証します.
\pi(s, a) > 0
ここで,sとaは,全ての行動と状態の対になります.
これによって,開始点探査を行う必要がなくなりました.(一定確率でランダムに行動するので,多くの状態を経験できるからです.)
ちょっと気になるのは方策改善.
前々回でいってたこれは,
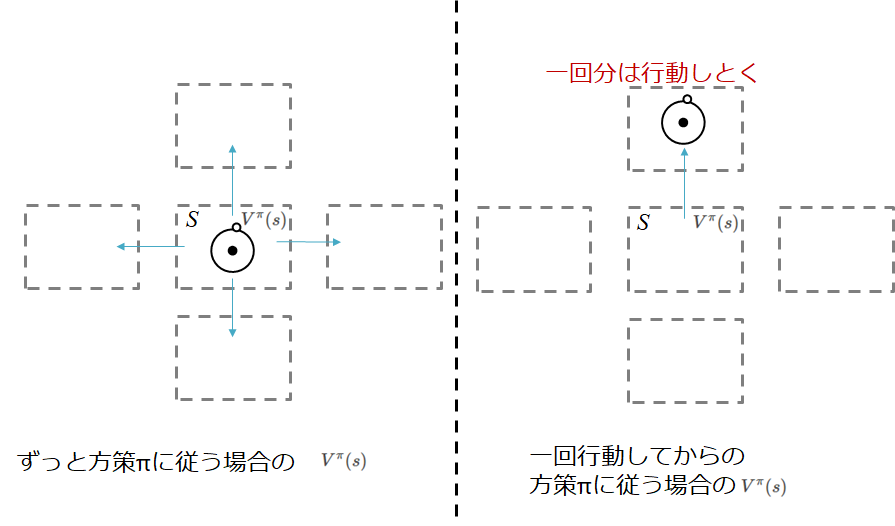
例えば,今ある状態$s$において行動$a$をとり,その後方策$\pi$に従った場合の状態価値が,状態$s$からずっと方策$\pi$にしたがった場合よりも大きければ...
行動を変えた方がいいことになります
図で表すとこんな感じ
この考え方?というかこれが成り立つことを方策改善定理といいます.
証明は本等にお預けします!が証明できます
そして,ここでgreedyという考えがでてきます
つまり,ある状態$s$において,その時にとれる最も高い報酬をもらえそうな行動を選択すれば,そのあとは最初から方策$\pi$によって行動するよりはいいだろってわけです.(すごく当たり前のことをいっています,方策$\pi$は確率ですからね,そりゃ最初の行動をもっともいいやつに確定させておけば高くなりますよね)
ちなみにこの考えは確率にも適用できます
つまり,その時にとれる最も高い報酬をもらえそうな行動に高い確率を振っておくということでも,この方策改善定理は成り立ちます
期待値が大きくなるので,なんとなくわかるかと思いますが
でポイントになるのは最後の部分です.
ようは方策評価後に,方策改善するときに,決定的に,一番いいやつを選ばずに,確率的に選べばよいのです.そうすれば,この定理はまだ成り立ちます.(期待値的に向上しますので)
方策OFF型
もう一つのアプローチを考えみます.
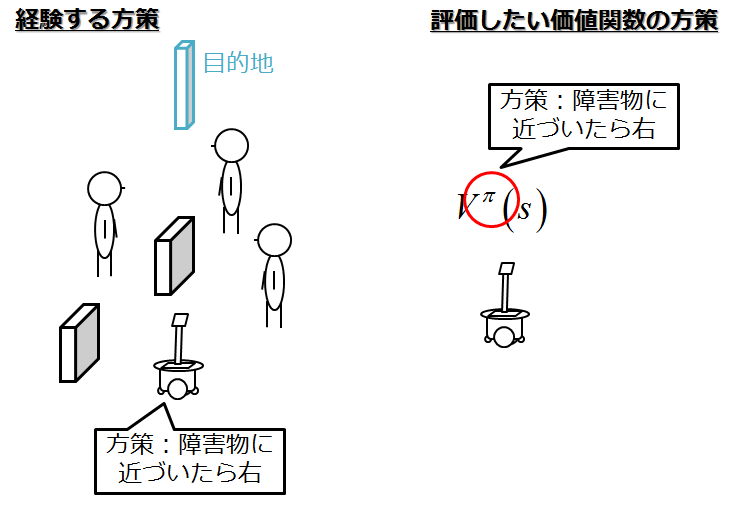
今まで,エピソードを行っている方策と,方策の価値関数の方策が一緒でした.
つまり,経験している動きの方策と,評価したい価値関数における方策が同じなのです.
そこで,それを変えることで評価できませんかね?と考えてみます.
つまり,実際に経験したエピソードでの,方策と,評価したい価値関数における方策を変えるのです.
いやそんなことありなのとなりそうですが,
相対的生起確率を考えるといけます.
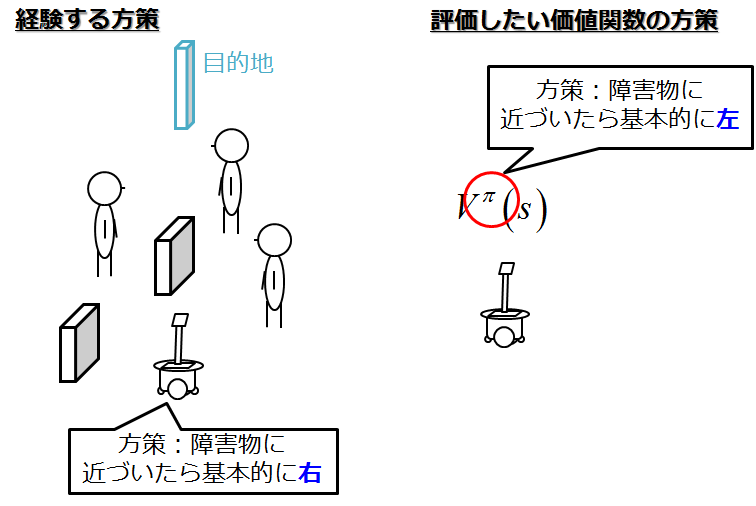
ようは,ある方策$\pi$で動いたときに,異なる方策$\pi'$で評価を行うというわけですが...
その生起確率を考えましょう
つまり詳細は教科書の式を参考にお願いしたいですが,
相対生起確率を以下のように定義します.
これは,ある方策$\pi$で動いたときに,異なる方策$\pi'$においては,それがどのくらい起こるのかを考えたものです
\frac{p_i(s_t)}{p'_i(s_t)} = \prod_{k=t}^{T_i(s)-1} \frac{\pi(s_k, a_k)}{\pi'(s_k, a_k)}
とするわけです.
そして,これを用いて,重みづけ平均をとります
V(s) = \frac {\sum_{k=t}^{n_s}\frac{p_i(s_t)}{p'_i(s_t)}R_i(s)}{ \sum_{k=t}^{n_s}\frac{p_i(s_t)}{p'_i(s_t)}}
これによって異なる方策も評価することができてしまいます.
混乱するポイント
基本的に,混乱しがちなのは,
- 方策評価(ある方策のもとでの行動価値,価値関数を求める)
- 方策改善(行動価値,価値関数をもとに,方策を改善する)
- 価値反復(GPI)
の3つを混合で考えてしまっているときです.
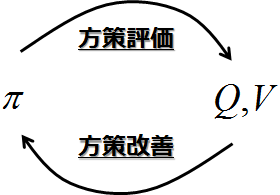
常に基本は
です.
これは変わりません.
ですが,まぁ永遠と方策評価をやっているわけにはいかないわけで
うまくそれをやれないかな?
っていうのが,価値反復(GPI)的な考え方です.
GPIは最適方策と最適価値関数(行動価値関数)は常にバランスしているという考えです.
どっちか片方がうまくいってなければ,バランスしません.
よって,方策評価が収束する前に,打ち切って,方策改善を行ってもうまくいくのではないかというわけです.
ちなみに,動的計画法では,これは,一回のスウィープ(全状態に対して行う)操作で行われ,
モンテカルロ法では,1エピソード毎に行われます.
今回は教科書に面白い問題がなさそうだったので,理論を中心に説明しました.
コードについてですが,基本的には,そこまで難しくはなさそうです.基本は同じです.