【機械学習】無相関化を数学から理解する

#1.導入
##(1)目的
機械学習をやってみたいと思った場合、scikit-learn等を使えば誰でも比較的手軽に実装できるようになってきています。
但し、仕事で成果を出そうとしたり、より自分のレベルを上げていくためには
**「背景はよくわからないけど何かこの結果になりました」**の説明では明らかに弱いことが分かると思います。

今回は**「無相関化」**を取り上げます。

「無相関化って聞いたことはあるけどなぜするの？」「どう使うの？」という前段の説明から、「無相関化って、数学的にはどのような処理が行われているの？」という疑問にも答えられるような記事にすることが目的です。

※今回は、しっかり理解しようとすると行列・共分散・固有値ベクトル・・等、諸々の理解が必要です。数学はあまり細かい点には行きすぎず、大枠の理解ができるように心がけました。

※調べている感じですと、無相関化が機械学習でそれ単独で使われることは少なそうです。どちらかというと主成分分析で使われるみたいです。

##(2)構成
まず2章で無相関化の概要を記載し、3章で実際に無相関化をしてみます。
最後に4章で、無相関化を数学的に理解できるような説明をしていきます。

※「数学から理解する」シリーズとして、いくつか記事を投稿していますので、併せてお読みいただけますと幸いです。
【機械学習】標準化すると平均0,標準偏差1になることを数学から理解する
【機械学習】決定木をscikit-learnと数学の両方から理解する
【機械学習】線形単回帰をscikit-learnと数学の両方から理解する
[【機械学習】線形重回帰をscikit-learnと数学の両方から理解する]
(https://qiita.com/Hawaii/items/b84a0d669bcf5267e750)
[【機械学習】ロジスティック回帰をscikit-learnと数学の両方から理解する]
(https://qiita.com/Hawaii/items/ee2a0687ca451fe213be)
[【機械学習】SVMをscikit-learnと数学の両方から理解する]
(https://qiita.com/Hawaii/items/4688a50cffb2140f297d)
[【機械学習】相関係数はなぜ-1から1の範囲を取るのか、数学から理解する]
(https://qiita.com/Hawaii/items/3f4e91cf9b86676c202f)

※その他技術的な内容やデータサイエンスについてもブログを書いていますので、
よろしければ遊びに来てください。

[データサイエンス　はじめの一歩]
(https://hazimenoippo-hawaii.com/)

#2.無相関化とは

その名の通り、各変数間の相関をなくすことです。
各変数間の相関が高いと、何が問題なのでしょうか？

##(1)なぜ無相関化する必要があるのか

結論から申し上げますと、**「偏回帰係数の分散が大きくなり、モデルの精度が不安定になりやすいから」**です。

・・・全然わからないですね。もう少し説明していきます。

例えば、回帰モデルの数式は一般に下記のように表されます。

$y = a_1x_1 + a_2x_2 + ・・+ b$

ここでいう$y$（目的変数）と$x_1$や$x_2$（説明変数）に実データを入れて、偏回帰係数の$a_1$や$a_2$、定数項の$b$を求めるのが重回帰分析です。

この偏回帰係数の分散（どれくらい偏回帰係数が色んな値を取りがちか、というイメージ）はどのように求められるかというと、細かく書くと混乱の元になるので結論だけ書きますと、「偏回帰係数の分散を求める式の分子に(1-相関係数)」が入っているのです。

つまり、相関が大きくなるほど分子が小さくなり、結果として偏回帰係数の分散が大きくなる＝偏回帰係数が色んな値を取りがち＝モデルの精度が不安定になる

という理屈です。

##(2)では、相関が高い変数は削除すればいい・・？
(1)で見たように、相関が高い変数があった場合どちらかを削除すればいいかというと、そういうわけでもありません。

なぜなら、「変数間の相関が高い」というのは「変数同士が線形の関係にある」ということを言っているだけです。
※ここが良くわからない方は、【機械学習】相関係数はなぜ-1から1の範囲を取るのか、数学から理解するの2章の注意点を参照ください。

→ですので安易に削除してしまうと、その変数が本当は持っていたかもしれない他の重要な情報を削除してしまう可能性があります。

##(3)じゃあ、どうすればいいかというと・・・
ここで登場するのが無相関化です。

各変数の相関を無くした上でモデル構築をしていきます。

イメージが付きづらいと思いますので、実際にやってみましょう。

#3.無相関化をやってみる
今回も具体例として、いつも利用するkaggleのkickstarter-projectsを例にします。
https://www.kaggle.com/kemical/kickstarter-projects

この章は長いですが、肝心の無相関化は(ⅶ)のみですので、先にそちらを見ていただくのもいいと思います。

※注意点※
・今回は、本来説明変数として無相関化した方がいい変数が見つからなかったので、
モデル構築には全く関係ない変数同士を無相関化しています。

あくまで、「無相関化とはこのようにやるのだ」と認識するための章だということをご了承ください。

・いつも私の記事の例で使うkickstarter projectsでまさに無相関化をされているサイトがありましたので、そちらを大変参考にさせていただきました。
https://ds-blog.tbtech.co.jp/entry/2019/04/27/Kaggle%E3%81%AB%E6%8C%91%E6%88%A6%E3%81%97%E3%82%88%E3%81%86%EF%BC%81_%EF%BD%9E%E3%82%B3%E3%83%BC%E3%83%89%E8%AA%AC%E6%98%8E%EF%BC%92%EF%BD%9E

###(ⅰ)インポート

#numpy,pandasのインポート
import numpy as np
import pandas as pd
import seaborn as sns

#日付データに一部処理を行うため、インポート
import datetime

###(ⅱ)データの読み込み

df = pd.read_csv("ks-projects-201801.csv")

###(ⅲ)データ数の確認
下記より、(378661, 15)のデータセットであることが分かります。

df.shape

###(ⅳ)データ成形
####◆募集日数
詳細は割愛しますが、クラウドファンディングの募集開始時期と終了時期がデータの中にありますので、これを「募集日数」に変換します。

df['deadline'] = pd.to_datetime(df["deadline"])
df["launched"] = pd.to_datetime(df["launched"])
df["days"] = (df["deadline"] - df["launched"]).dt.days

####◆目的変数について
こちらも詳細は割愛しますが、目的変数である「state」が成功（"successful")と失敗("failed")以外にもカテゴリがありますが、今回は成功と失敗のみのデータにします。

df = df[(df["state"] == "successful") | (df["state"] == "failed")]

この上で、成功を1、失敗を0に置き換えます。

df["state"] = df["state"].replace("failed",0)
df["state"] = df["state"].replace("successful",1)

###(ⅴ)欠損値処理
結論ありきで申し訳ないのですが、この後使っていくのがused pledgedのため、この変数のみ欠損値処理をします。

df["usd pledged"] = df["usd pledged"].fillna(df["usd pledged"].mean())

###(ⅵ)相関係数の確認
各変数の相関を確認してみます。

sns.heatmap(df.corr())

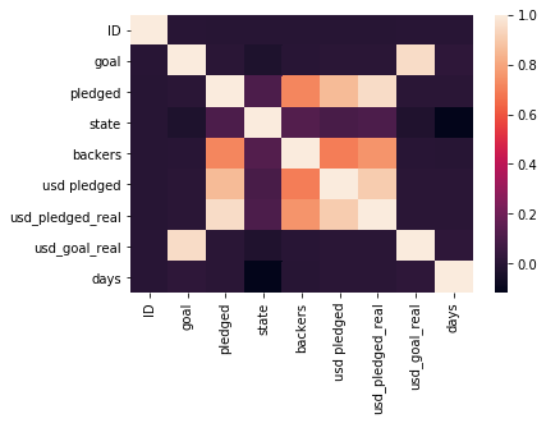
ここで、変数間の相関が高い「pleged」と「used pleded」を無相関化してみましょう。
※繰り返しになりますが、この処理自体はモデル構築に一切関係がありません。

###(ⅶ)無相関化

無相関化自体は下記のようにコードを書けば大丈夫です。
ただ、意味が分からないと思うのですが、今回は「そういうものなのだ」と読み進めていただき、4章の「数学から理解する」をご覧ください。

#pledgedとused plegedだけをdf_pledgedに格納
df_corr = pd.DataFrame({'pledged' : df['pledged'], 'usdpledged' : df['usd pledged']})

# 分散・共分散を求める
cov = np.cov(df_corr, rowvar=0) 

# 分散共分散行列の固有ベクトルをSへ代入
_, S = np.linalg.eig(cov)           

#データを無相関化 ※.Tは転置を表す
pledged_decorr = np.dot(S.T, df_corr.T).T 

これで無相関化完了です。
試しに、pledgedとusedplegedの相関係数を確認してみましょう。

print('相関係数: {:.3f}'.format(np.corrcoef(pledged_decorr[:, 0], pledged_decorr[:, 1])[0,1])) 

こうすると、「相関係数：0.000」と表示されます。
無事に無相関化することができました！

#4.無相関化を数学から理解する
##(1)前提
さて、この章では実際に無相関化を数学的にはどのように処理しているのか見ていきましょう。
冒頭でも記載しましたが、無相関化を理解するには「行列」や「固有値・固有ベクトル」の考え方が必要になります。

難しいと感じる方は読み飛ばしていただいてもいいですし、説明自体は細かくはせず、ざっくり言うとこんな形・・という説明になっております。

##(2)具体例
いくつか説明変数があったとして、それをそれぞれ$\boldsymbol{x_1}$,$\boldsymbol{x_2}$・・・$\boldsymbol{x_n}$とします。
※例えば先ほどの例で言うとpledgedが$\boldsymbol{x_1}$,usdpledgedが$\boldsymbol{x_2}$です。

この各変数間の分散・共分散行列は下記のように書くことができます。

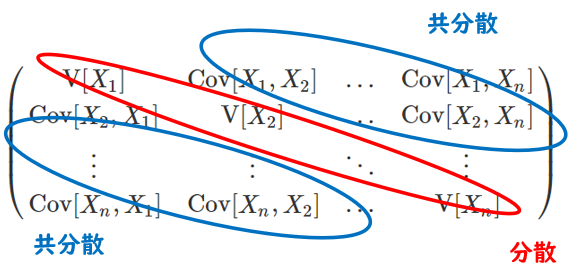
青枠に各変数の2つずつの組み合わせの共分散、赤枠には各変数の分散が入ります。

※いきなり行列が出てきて拒否反応が出る方がいらっしゃるかもしれないですが、行列をわかってくださいというよりも、ここでは**「全変数の中で2つペアずつの共分散が青枠にあり、赤枠には各変数の分散が入っているのだ」**と理解してください。

この分散・共分散行列を、対角化という処理をすると、下記のように変身します！
※対角化とは何か、は主旨からずれるので割愛します。

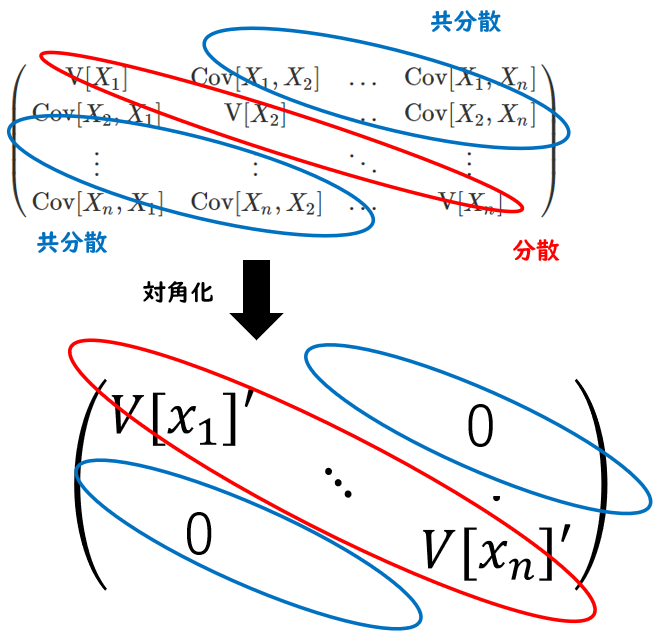
・・・ちょっとよくわからないと思います。
ここで大切なのは、青枠（共分散）が全て0になっていることです。

対角化をすると共分散を0にすることができ、まさにこれが無相関化の処理と同義と言えます。

ではなぜ、各変数間の共分散が0になれば、無相関化したといえるのでしょうか。

それを理解するために、相関係数の公式を思い出しましょう。
相関係数をrとおくと、rは下記のように導かれます。

（相関係数r） = (共分散）／　（$x$の標準偏差）・($y$の標準偏差)

この式から、共分散が0になる、すなわち分子が0になるので、相関係数が0になることがわかります。

だからこそ対角化で各変数間の共分散を0にし、相関係数を0にすることで無相関化を成し遂げていたというのが今回の結論です。

#5.結び
以上、いかがでしたでしょうか。
私の思いとして、「最初からものすごい複雑なコードなんて見せられても自分で解釈できないから、精度は一旦どうでもいいのでまずはscikit-learn等で基本的な一連の流れを実装してみる」ことは非常に重要だと思っています。

ただ、慣れてきたらそれらを裏ではどのように動かしているのか、数学的な背景から理解していくことも非常に重要だと感じています。

とっつきづらい内容も多いと思いますが、少しでも理解の深化の助けとなりましたら幸いです。