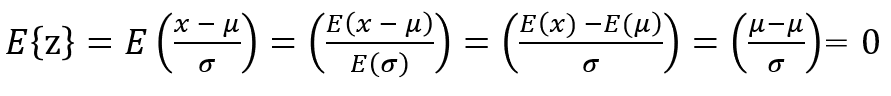【機械学習】標準化すると平均0,標準偏差1になることを数学から理解する

1.目的

機械学習をやってみたいと思った場合、scikit-learn等を使えば誰でも比較的手軽に実装できるようになってきています。
但し、仕事で成果を出そうとしたり、より自分のレベルを上げていくためには
「背景はよくわからないけど何かこの結果になりました」の説明では明らかに弱いことが分かると思います。

今回は前処理で登場する「標準化」を取り上げます。

「標準化って聞いたことはあるけどなぜするの？」「scikit-learnではどう使うの？」という前段の説明から、「標準化は”平均0、標準偏差1にするような処理”としかしらないけど、実際にはどのような計算になっているのか、数式から理解したい」という疑問にも答えられるような記事にすることが目的です。

まず2章で標準化の概要を記載し、3章で実際にscikitlearnを使って標準化をしてみます。
最後に4章で、標準化の数式（標準化したら本当に平均0、標準偏差1になるか）について触れたいと思います。

※「数学から理解する」シリーズとして、いくつか記事を投稿していますので、併せてお読みいただけますと幸いです。
【機械学習】決定木をscikit-learnと数学の両方から理解する
【機械学習】線形単回帰をscikit-learnと数学の両方から理解する
【機械学習】線形重回帰をscikit-learnと数学の両方から理解する
【機械学習】ロジスティック回帰をscikit-learnと数学の両方から理解する
【機械学習】SVMをscikit-learnと数学の両方から理解する
【機械学習】相関係数はなぜ-1から1の範囲を取るのか、数学から理解する

2.標準化とは

(1)標準化とは

結論から言うと、各変数を「平均0、標準偏差1」に収まるように加工する処理のことを言います。

機械学習では前処理でよく使われます。

ざっくり言うと、各データの単位をそろえてあげるイメージです。
例えば売上と気温というデータがあるとき、売上は億単位、気温は最高でも40(℃)くらいとなるとスケールが全然違うので、この2つのデータをそれぞれが平均0、標準偏差1におさまるように変換してあげます。
（具体的には、標準化後は売上0.4、気温0.1という具合です。※数値は適当です）

(2)なぜ標準化をするの？

色々な理由があるようですが、その内の1つに「機械学習の多くのアルゴリズムは各変数のスケールが同じであることを前提としている」ことが挙げられます。

例えば先ほど挙げた売上（4億円とする）と気温（35℃とする）の例も、私たち人間は事前に各データが「売上」「気温」であることを知っているため、2つの変数のスケール（単位の規模）が異なっていても違和感なく理解できます。

しかし、コンピュータはそんなことは意識しないため、「400,000,000」と「35」というただの数値と捉え、機械学習において誤った意味付けをしてしまう場合があります。

このような弊害をなくすため、事前に各変数のスケールを合わせる、標準化を行います。

(3)標準化以外にやり方はあるの？

各変数のスケールを合わせる手法は標準化以外にも、正規化という手法があります。

今回は深くは触れないですが、「外れ値の影響を受けにくい」「標準化すると正規分布にもなる」ことから、標準化が行われる場面が多いようです。

3.scikit-learnで標準化

今回も具体例として、いつも利用するkaggleのkickstarter-projectsを例にします。
https://www.kaggle.com/kemical/kickstarter-projects

この章は長いですが、肝心の標準化は(ⅴ)のみですので、先にそちらを見ていただくのもいいと思います。

(ⅰ)インポート

#numpy,pandasのインポート
import numpy as np
import pandas as pd

#日付データに一部処理を行うため、インポート
import datetime

#訓練データとテストデータ分割のためにインポート
from sklearn.model_selection import train_test_split

#標準化のためにインポート
from sklearn.preprocessing import StandardScaler

#精度検証のためにインポート
from sklearn.model_selection import cross_val_score

#ロジスティック回帰のためにインポート
from sklearn.linear_model import SGDClassifier
from sklearn.metrics import log_loss, accuracy_score, confusion_matrix

(ⅱ)データの読み込み

df = pd.read_csv("ks-projects-201801.csv")

(ⅲ)データ数の確認

下記より、(378661, 15)のデータセットであることが分かります。

df.shape

(ⅳ)データ成形

◆募集日数

詳細は割愛しますが、クラウドファンディングの募集開始時期と終了時期がデータの中にありますので、これを「募集日数」に変換します。

df['deadline'] = pd.to_datetime(df["deadline"])
df["launched"] = pd.to_datetime(df["launched"])
df["days"] = (df["deadline"] - df["launched"]).dt.days

◆目的変数について

こちらも詳細は割愛しますが、目的変数である「state」が成功（"successful")と失敗("failed")以外にもカテゴリがありますが、今回は成功と失敗のみのデータにします。

df = df[(df["state"] == "successful") | (df["state"] == "failed")]

この上で、成功を1、失敗を0に置き換えます。

df["state"] = df["state"].replace("failed",0)
df["state"] = df["state"].replace("successful",1)

◆不要な行の削除

モデル構築の前に、不要だと思われるidやname（これは本来は残しておくべきかもしれないですが今回は消します）、そしてクラウドファンディングをしてからでないとわからない変数を削除します。

df = df.drop(["ID","name","deadline","launched","backers","pledged","usd pledged","usd_pledged_real","usd_goal_real"], axis=1)

◆カテゴリ変数処理

pd.get_dummiesでカテゴリ変数処理を行います。

df = pd.get_dummies(df,drop_first = True)

(ⅴ)標準化

いよいよ標準化です。
その前に、現時点のデータをざっと見てみましょう。

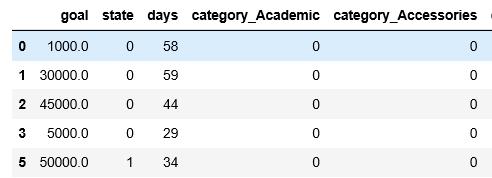
冒頭の例で挙げたように、「goal（目標金額）」と「days（募集期間）」の単位スケールが結構違うことが分かります。

今回は、この2変数を標準化してみましょう。

stdsc = StandardScaler()
df["goal"] = stdsc.fit_transform(df[["goal"]].values)
df["days"] = stdsc.fit_transform(df[["days"]].values)

この処理をした上で、再度データを表示してみましょう。

goalとdaysのデータが標準化されました！

(ⅵ)ロジスティック回帰実装

標準化の処理自体は(ⅴ)で終わりですが、一連の流れを把握するという目的で、
ロジスティック回帰モデル構築まで行います。

#訓練データとテストデータに分割
y = df["state"].values
X = df.drop("state", axis=1).values
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=1234)

#ロジスティック回帰モデル構築
clf = SGDClassifier(loss = "log", penalty = "none",random_state=1234)
clf.fit(X_train,y_train)

#テストデータで精度確認
clf.score(X_test, y_test)

これで、精度は0.665と出てきました。

※補足
今回の(ⅴ)標準化がない場合、精度は0.529になりますので、モデル全体の精度が向上していることが分かります。

4.標準化を数学から理解する

ここまでは、標準化をとりあえず実装できるようにする目的でscikit-learnを使って標準化を行ってきました。

この章では、標準化が行っている処理を数学の観点から理解していきたいと思います。

(1)標準化の数式

では、ここで具体例を出していきましょう。冒頭に挙げたような、気温と売上の例です。

	気温	売上（円）
1	10	400,000,000
2	15	390,000,000
3	30	410,000,000
4	20	405,000,000
5	40	395,000,000

まず結論から出します。
標準化は、下記の数式で求められます。

z =  \frac{x -u}{σ}

よくわからないですね。
$x$は各変数のそれぞれの値、$u$は各変数の平均、$σ$は各変数の標準偏差です。

ものすごくざっくりした言い方ですと、各値から平均を引いて、各変数の標準偏差、つまり散らばり具合で割っているので、色んな範囲に点在しているデータが、ぎゅっと寄せ集められるイメージです。

・・もっとよくわからないですね。
実際に数値を求めてみましょう。

■平均$u$
$u$は平均なので、気温の5つのデータ全ての平均を計算すると、$(10+15+30+20+40)/5 = 23$になります。

同様に、売上の平均を計算すると、$(400,000,000 + 390,000,000 + 410,000,000 + 405,000,000 + 395,000,000)/5 = 400,000,000$
となります。

■標準偏差$σ$
計算過程は割愛しますが、
気温の標準偏差を計算すると約12になります。

売上の標準偏差は7,905,694になります。

■標準化すると・・
下記の様な計算結果になり、標準化した気温列の数値と、標準化した売上列の数値を機械学習では使っていくということです。

	気温	売上（円）	標準化した気温	標準化した売上
1	10	400,000,000	$(10-23)/12$	$(400,000,000-400,000,000)/7905694$
2	15	390,000,000	$(15-23)/12$	$(390,000,000-400,000,000)/7905694$
3	30	410,000,000	$(30-23)/12$	$(410,000,000-400,000,000)/7905694$
4	20	405,000,000	$(20-23)/12$	$(405,000,000-400,000,000)/7905694$
5	40	395,000,000	$(40-23)/12$	$(395,000,000-400,000,000)/7905694$

(2)なぜ平均0、標準偏差1になるの？

標準化の数式は$z = \frac{x -u}{σ}$と記載しましたが、この計算をすると平均0、標準偏差1になる証明をしていきましょう。

ここでは、$y = ax +b$の式で考えていきます。

＜標準化していない、元の式の平均と標準偏差＞

まず、シンプルに標準化前の平均と標準偏差を求めましょう。
求めてみるとわかりますが、平均も標準偏差も0や1ではありません。
■平均
下記のように、$y$の平均は$aµ+b$と表せます。

※$E$は期待値を表していますが、期待値があまりわからない方はざっくり「平均」と捉えていただいても大丈夫です（厳密には異なります）。

■標準偏差
まず分散を求めていて、結果は$a^2σ^2$です。（標準偏差は$aσ$)

＜標準化した式の平均と標準偏差＞

では次に、標準化した後の平均と標準偏差を求めていきましょう。
式変形の考え方は、基本的に標準化前の式変形と同じです。

下記のように式変形をすると、標準化した後は平均0、標準偏差1になっていることがわかります！

■平均

■標準偏差
こちらも先ほど同様、まずは分散を求めています。分散が1になるので、結局標準偏差も1になります。

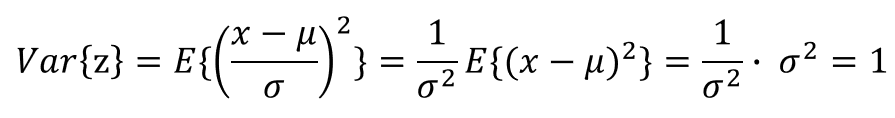
以上で、標準化した後の各変数の平均は0、標準偏差が1になっていることが数式から証明することができました！

5.結び

以上、いかがでしたでしょうか。
私の思いとして、「最初からものすごい複雑なコードなんて見せられても自分で解釈できないから、精度は一旦どうでもいいのでまずはscikit-learn等で基本的な一連の流れを実装してみる」ことは非常に重要だと思っています。

ただ、慣れてきたらそれらを裏ではどのように動かしているのか、数学的な背景から理解していくことも非常に重要だと感じています。

とっつきづらい内容も多いと思いますが、少しでも理解の深化の助けとなりましたら幸いです。