1.目的
機械学習をやってみたいと思った場合、scikit-learn等を使えば誰でも比較的手軽に実装できるようになってきています。
但し、仕事で成果を出そうとしたり、より自分のレベルを上げていくためには
「背景はよくわからないけど何かこの結果になりました」の説明では明らかに弱いことが分かると思います。
この記事では、2~3で「理論はいいからまずはscikit-learn使ってみる」こと、4以降で「その背景を数学から理解する」2つを目的としています。
※私は文系私立出身なので、数学に長けていません。可能な範囲で数学が苦手な方にもわかりやすいように説明するよう心がけました。
※線形単回帰Verでも同様の記事を投稿していますので、併せてお読みいただけますと幸いです。
【機械学習】線形単回帰をscikit-learnと数学の両方から理解する
※2020.7.26 4.ロジスティック回帰を数学から理解するの(2)を一部追記
2.ロジスティック回帰とは
ロジスティック回帰とは、ベルヌーイ分布に従う変数の統計的回帰モデルの一種です。
出典:【Wikipedia】(https://ja.wikipedia.org/wiki/ロジスティック回帰)
よくわからないと思うので簡単に言いますと**「ある事象が起きる確率を予測」したり、「その確率をもとに分類を行う」こと**に使われます。
ですので、機械学習を用いて分類を行いたい場合や、その確率を予測したいという場合にロジスティック回帰は使われます。
(私は機械学習を勉強しているときに、「確率を予測」できることに非常に驚きました。)
◆シグモイド関数(ロジスティック関数)について
では、このロジスティック回帰とはどのように分類や確率の予測を行っているのでしょうか。
細かい説明は数学の章に回そうと思うので割愛しますが、「ある事象が起きる確率を予測」とは、下記の「シグモイド関数」に必要な情報を入力するとその事象(Aとします)が発生する確率が算出されることを指します。
そして、その確率が50%以上であればAと分類され、確率が50%より小さければAではないと分類されるというわけです。
※ですので「確率の予測」と「分類」は切り離して考えるべきではなく、まずその事象が発生する確率を算出し、50%を境界としてA or notAで分類しているだけと考えればOKです。
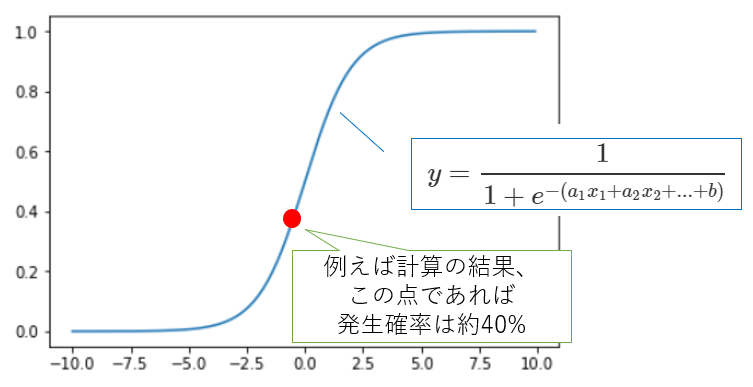
ちなみにシグモイド関数とは、下記のように定義されます。
※数学の章で再度出てくるので、読み飛ばしていただいても結構です。
y = \frac{1}{1 + e^{-(a_1x_1 + a_2x_2 + ... + b)}}
この計算の結果、出てきた$y$がその事象が発生する確率を表しており、ロジスティック回帰はこの確率を計算します。
例えば上のシグモイド関数上につけた赤い点であれば発生確率は40%と予測され、50%より小さいので事象Aは起きない、と分類されます。
◆分類とは
上記に記載した「分類」ですが、機械学習では主に「回帰(数値を予測すること)」か「分類」を行います。
分類はその名の通り、「AかBか」を分類したい場合に使います。
※例えば「株価は明日上がるか下がるか」といったような具合です。どのような目的設定をするかによって、分類は非常に有効な手法だと思います。
◆具体例
※この具体例はあまり実用的ではない具体例です。自分の場合は、国語の点数は●●のデータで・・といったように思いを馳せながら読んでいただければと思います。
15名分の生徒の中学~高校の国語・数学の全体平均点と、その生徒はその後文系、理系どちらに進学しているかのデータが手元にあるとします。

このデータをもとに、今後別の生徒の国語・数学のデータを使って、将来彼らが文系、理系どちらに進学するのか予測したいとします。
15名分の生徒の国語・数学の全体平均点の分布は下記のようになっています。
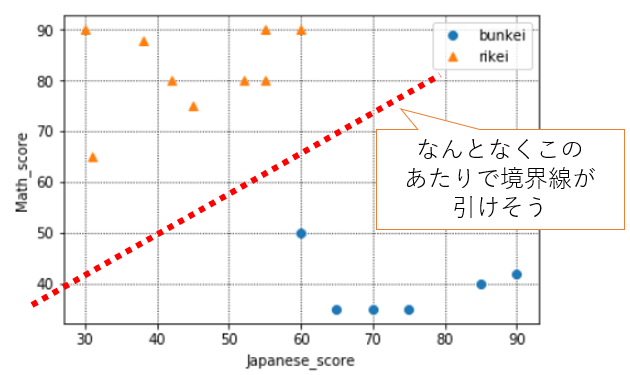
なんとなく、青い点(文系)とオレンジの点(理系)の間には境界がありそうですね。
次から、scikit-learnを使ってロジスティック回帰分析を行い、文系と理系で分類するモデルを作ってみましょう。
3.scikit-learnでロジスティック回帰
(1)必要なライブラリのインポート
ロジスティック回帰を行うために必要な下記をインポートしておく。
from sklearn.linear_model import SGDClassifier
from sklearn.metrics import log_loss, accuracy_score, confusion_matrix
# 2020年9月13日追加
import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
(2)データの準備
国語と数学の点数と、文理(文系がTrue,理系がFalse)を下記のようにdataとして設定する。
※例えば、最初の生徒は中学~高校の平均点が国語45点、数学75点で最終的に理系に進学したということ。
data = pd.DataFrame({
"bunri":[False,True,False,True,True,False,True,False,True,False,False,True,False,False,False],
"Japanese_score":[45, 60, 52, 70, 85, 31, 90, 55, 75, 30, 42, 65, 38, 55, 60],
"Math_score":[75, 50, 80, 35, 40, 65, 42, 90, 35, 90, 80, 35, 88, 80, 90],
})
(3)図示してみる(重要)
国語・数学の点数と文理を図示してみる。特徴をつかむためにも、いきなりscikit-learnを使うのではなく、どのようなデータでも図示することを心がけましょう。
y = data["bunri"].values
x1, x2 = data["Japanese_score"].values, data["Math_score"].values
# データをプロット
plt.grid(which='major',color='black',linestyle=':')
plt.grid(which='minor',color='black',linestyle=':')
plt.plot(x1[y], x2[y], 'o', color='C0', label='bunkei')#青い点:yがTrue(=文系)のもの
plt.plot(x1[~y], x2[~y], '^', color='C1', label='rikei')#オレンジの点:yがFalse(=理系)のもの
plt.xlabel("Japanese_score")
plt.ylabel("Math_score")
plt.legend(loc='best')
plt.show()

青(文系)とオレンジ(理系)には明確な切り分けができそうですね。
(現実世界ではここまで明確に分かれそうなことはあまりないです)
ロジスティック回帰モデルを構築していきましょう。
(4)モデル構築
(ⅰ)データ整形
まずはモデル構築をするためにデータの形を整えていきます。
y = data["bunri"].values#先ほどの図示と同じなので割愛してもOK
X = data[["Japanese_score", "Math_score"]].values
今回はpython文法の記事ではないので詳細は割愛しますが、xとyをscikit-learnでロジスティック回帰するための形に整えます。
※このあたりもある程度しっかりわかっていないと書けないコードだと思うので、どこかでまとめたいと思っています。
(ⅱ)モデル構築
いよいよ、モデル構築のコードです。
clf = SGDClassifier(loss='log', penalty='none', max_iter=10000, fit_intercept=True, random_state=1234, tol=1e-3)
clf.fit(X, y)
単純なモデルであればこれで終わりです。
clfという変数にこれからロジスティック回帰モデルを作ります!と宣言のようなことを行い、次の行で、そのclfに準備したXとyをフィット(=学習)させるというイメージです。
(ⅲ)パラメータを出してみる
※(ⅲ)は、難しければ最低限という意味では不要なので飛ばしてください。
突然パラメータという言葉が出てきましたが、これは冒頭のシグモイド関数で記載した$y = \frac{1}{1 + e^{-(a_1x_1 + a_2x_2 + ... + b)}}$の$a$と$b$のことを指します。
今回の例では説明変数は国語の点数と数学の点数の2つなので、$y = \frac{1}{1 + e^{-(a_1x_1 + a_2x_2 + b)}}$と定義でき、$a$と$b$は下記のようにscikit-learnで計算できます。
# 重みを取得して表示
# 2020年9月13日修正(Beforeではw0:b、w1:a1、w2:a2と記載しておりました)
w0 = clf.intercept_[0]
w1 = clf.coef_[0, 0]
w2 = clf.coef_[0, 1]
そうするとb = 4.950, a1 = 446.180, a2 = -400.540と表示されると思いますので、$y = \frac{1}{1 + e^{-(446.180x_1 + (-400.540)x_2 + 4.950)}}$というシグモイド関数であることがわかります。
(ⅳ)補足
◆SGDClassifierについて
ロジスティック回帰であればScikit-learnでは「LogisticRegression」でもモデル構築可能です。
SGDClassifierとは確率的勾配降下法でモデルを構築したい場合に使用します。
◆パラメータについて
モデル構築で使用しているパラメータを簡単に補足します。
・loss:損失関数を何に設定するか。logにすることで、ロジスティック回帰と同義になります。デフォルトはhinge(ヒンジ損失関数)で、SVMに使用されます。
・penalty:罰則をどのように設けるか。デフォルトはl2(L2正則化)。
・max_iter:最大のエポック数を設定する。エポック数とは、「一つの訓練データを何回繰り返して学習させるか」の数のこと。
・fit_intercept:Falseにすると切片が0に設定される。デフォルトはTrue。
・random_state:データを分割したりする際の乱数のシード値。これを同じ数値にすることで、毎回同じ結果が得られるようにする。
・tol:どれくらいで処理を停止させるかの基準のこと。ここはあまりきちんと説明されたサイトや書籍を見つけられていないのですが、おそらく膨大なデータを扱う際の処理時間に影響すると思われます。
(5)構築したモデルを図示してみる
それでは、この境界を先ほどの散布図に図示してみましょう。
※このコードは少し難しいので、理解せず、コピペだけでもOKです。scikit-learnではこのような境界線を学習から算出し、この境界より右下だと文系、左上だと理系と判別しているのだと認識していただければ大丈夫です。
y = data["bunri"].values
x1, x2 = data["Japanese_score"].values, data["Math_score"].values
# データをプロット
plt.grid(which='major',color='black',linestyle=':')
plt.grid(which='minor',color='black',linestyle=':')
plt.plot(x1[y], x2[y], 'o', color='C0', label='bunkei')#青い点:yがTrue(=文系)のもの
plt.plot(x1[~y], x2[~y], '^', color='C1', label='rikei')#オレンジの点:yがFalse(=理系)のもの
plt.xlabel("Japanese_score")
plt.ylabel("Math_score")
plt.legend(loc='best')
# 境界線をプロットして表示
# 紫:境界線
line_x = np.arange(np.min(x1) - 1, np.max(x1) + 1)
line_y = - line_x * w1 / w2 - w0 / w2
plt.plot(line_x, line_y, linestyle='-.', linewidth=3, color='purple', label='kyoukai')
plt.ylim([np.min(x2) - 1, np.max(x2) + 1])
plt.legend(loc='best')
plt.show()
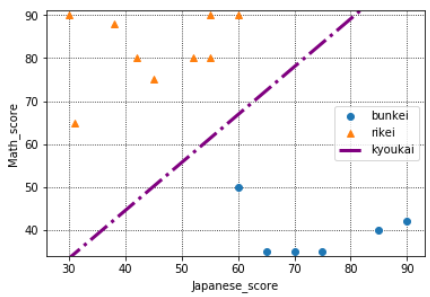
このように、scikit-learnで何を出していて、どういうことにつながっているのかを意識するようにしましょう。
(6)現実世界では・・
モデルを作って終わり、では意味ないですね。現実世界では、この予測モデルを使って、別の生徒の文理を予測していくことが必要です。
あなたは別の5人分の情報を得て、データをメモしました。
それを下記のようにzという変数に格納します。
z = pd.DataFrame({
"Japanese_score":[80, 50, 65, 40, 75],
"Math_score":[50, 70, 55, 50, 40],
})
z2 = z[["Japanese_score", "Math_score"]].values
やりたいのは、先ほどscikit-learnで求めたロジスティック回帰モデルに、上記の別の生徒のデータをあてはめ、文理を予測することです。
y_est = clf.predict(z2)
このようにすると、y_estには「([True, False, True, False, True])」と結果が表示されます。
つまり、1人目は国語が80点、数学が50点なので文系と予測されている・・という形です。
国語と数学の点数から文理が予測できるということになり、あなたの目標は達成されます。
また、冒頭で記載した「文系である確率」を表示してみましょう。
clf.predict_proba(z2)
このように記載すると文系である確率と、文系でない確率が2列分表記されます。
ただ、今回の例はあまりにわかりやすい例にしてしまったので、結果が下記のように表示され、確率が0%か100%にはっきりわかれてしまいました。
※右側が文系である確率です。
[0., 1.],
[1., 0.],
[0., 1.],
[1., 0.],
[0., 1.]
4.ロジスティック回帰を数学から理解する
さて、3まではscikit-learnを用いてロジスティック回帰モデルを構築→図示→別の5名の生徒の文理を予測するという流れを実装してみました。
ここでは、この流れのロジスティック回帰モデルは、数学的にはどのように計算されているのかを明らかにしていきたいと思います。
※現状はこの知識は必要ないという方は読み飛ばしていただいて結構です。
(1)前提知識
積の対数について下記を使います。
$log_aMN = log_aM + log_aN$
(2)シグモイド関数とは
2.の「◆シグモイド関数(シグモイド関数)について」にも少し記載しましたが、シグモイド関数はある事象を確率で表現するための関数のことで、下記のような形をしています。
※$y$軸の最大値が1(確率100%)、最小値は0(確率0%)です。

また、この青い関数は下記のように定義されます。
y = \frac{1}{1 + e^{-(a_1x_1 + a_2x_2 + ... + b)}}
上記の$a_1$や$a_2$、そして$b$はいわゆるパラメータといわれるもので、一次関数の$y = ax + b$の$a$や$b$と位置づけは同じです。
そして$x_1$や$x_2$がいわゆる説明変数といわれるもので、今回でいうと国語の点数が$x_1$、数学の点数が$x_2$にあたります。
この$a_1$と$a_2$、そして$b$を良いかんじの数値に決めてあげれば、あとは新規で取得した生徒の国語と数学の点数を$x_1$と$x_2$に入力すると、文系になる確率(or理系になる確率)が$y$として計算できるというわけです。
つまり機械学習のロジスティック回帰ではこのパラメータ$a$や$b$を計算してシグモイド関数を算出しているのです。
文章ばかりだとイメージがわきづらいと思うので、次から具体的な数値をあてはめて計算してみましょう。
(2)-2020.7.26追記 なぜシグモイド関数の形になるのか?
(3)に進む前に、そもそもなぜロジスティック回帰においてシグモイド関数を使うのか追記していきます。
(ⅰ)ロジスティック回帰のモチベーション
まず重要な点として、ロジスティック回帰では質的データ(0,1)も、回帰として扱えるようにしたいというモチベーションがあります。
しかし、そのためには質的データだと0~1の範囲しか数値を扱えないので、何とかしてこの数値範囲の制限をなくしていきたいです(=-∞~∞にする)。
(ⅱ)STEP1 まずは範囲を0~∞にする
例えば$y$が{0,1}を取る質的データだとします。
これを、オッズの定義から、$\frac{y}{1 - y }$ と変形します。
これは、イメージとしては「$y$へのなりやすさ」です。
このように変換すると、範囲は0~∞になります。($\frac{y}{1 - y }$の形はマイナスにはならないですよね)
(ⅲ)STEP2 対数を取って-∞~∞にする
(ⅱ)の$\frac{y}{1 - y }$の対数を取り、$log\frac{y}{1 - y }$に変形すると、対数の性質から、範囲は-∞~∞にすることができます。
ここまでで、範囲を-∞~∞にすることができたので、ここでようやく回帰のように扱うことができます。
STEP3から、回帰として扱った場合の式変形を見ていきましょう。
(ⅳ)STEP3 回帰として式変形を行う
先ほどの$log\frac{y}{1 - y }$を回帰として扱えるようになったので、下記のようにおいてみましょう。
$log\frac{y}{1 - y }$ = $ax + b$
これを式変形すると、
$\frac{y}{1 - y }$ = $e^{(ax + b)}$ となります。さらに式変形すると、
$y = (1 - y)e^{(ax + b)}$ となります。さらに式変形していきましょう。
$y = e^{(ax + b)} - y・e^{(ax + b)}$ だんだんゴールに近づいてきています。さらに式変形しましょう。
$(1 + e^{(ax + b)})y = e^{(ax + b)}$
$y = \frac{e^{(ax + b)}}{1 + e^{(ax + b)} }$ この式の分母と分子に$e^{-(ax + b)}$をかけます。
すると、$y$は下記のように最終的に式変形できます。
$y = \frac{1}{1 + e^{-(ax + b)} }$
この形は、(2)のシグモイド関数の形と同じであることがわかります!
(今回は単回帰分析のように$y = ax + b$とおいています)
まとめると、ロジスティック回帰でシグモイド関数を使うのは、
「質的データを回帰のように扱いたい」というモチベーションから、オッズの定義も利用して式変形を行い、回帰のように扱えるよう形にします。
その結果を$y = ax + b$とおき、式変形を行うと、最終的にシグモイド関数の形になるというわけです。
(3)数学的な理解
(ⅰ)シグモイド関数を1つずつデータにあてはめる
「データの準備」でセットした「data」を表形式に整理し、かつ一番右にシグモイド関数にするとどうなるのかをまとめています。
今回は「文系である確率」を求めようと思いますので、文系を1、理系を0にしておきます(逆に理系である確率を求めたければ理系を1、文系を0にします)。
| 生徒 | 国語点数 | 数学点数 | 文理(0:理系 1:文系) | シグモイド関数 |
|---|---|---|---|---|
| 1人目 | 45 | 75 | 0 | $\frac{1}{1 + e^{-(45a_1 + 75a_2 + b)}}$ |
| 2人目 | 60 | 50 | 1 | $\frac{1}{1 + e^{-(60a_1 + 50a_2 + b)}}$ |
| ・・・ | ・・・ | ・・・ | ・・・ | ・・・ |
| 15人目 | 60 | 90 | 0 | $\frac{1}{1 + e^{-(60a_1 + 90a_2 + b)}}$ |
(ⅱ)最尤推定量を求める
さて、パラメータ$a$(今回の例では$a_1$と$a_2$)と$b$を求めるにはどのようにすればいいのでしょうか。
結論から言うと、文系である確率を1人目から15人目まで掛け算し、その積が最大になる$a_1$と$a_2$と$b$を求めればいいのです。
これを最尤推定量といいます。
◆最尤推定量とは
「さいゆうすいていりょう」と読み、「最も尤(もっと)もらしい」推定値という意味です。
→ややこしいですが、「一番良さげな数値」という解釈で結構です。
◆掛け算してみましょう
文系である確率を1人目から15人目まで掛け算すると下記のようになります(Lとします)。
L = [1 - \frac{1}{1 + e^{-(45a_1 + 75a_2 + b)}}] × [\frac{1}{1 + e^{-(60a_1 + 50a_2 + b)}}] × ・・\\
× [1 - \frac{1}{1 + e^{-(60a_1 + 90a_2 + b)}}]
※1人目と15人目で1から引いているのは、1人目と15人目は理系なので、シグモイド関数の値自体は理系である確率のため、1から引くことで文系である確率に直しているからです。
◆Lの最大値を求めるために、対数に直す
イメージがつくかもしれませんが、Lは15人分掛け算がされています。これが、データが何百万人分・・となると計算が非常に難しくなるので、対数に直してあげます。
logL = log[1 - \frac{1}{1 + e^{-(45a_1 + 75a_2 + b)}}] + log[\frac{1}{1 + e^{-(60a_1 + 50a_2 + b)}}] + ・・\\
log[1 - \frac{1}{1 + e^{-(60a_1 + 90a_2 + b)}}]
◆パラメータを求める
$logL$を最大にするパラメータ$a_1$、$a_2$、$b$をどのように求めるかというと、解析的(=手計算)に出すことはできません。
scikit-learnでは、**"確率的勾配法"**を用いて最適なパラメータを算出してくれます。
※確率的勾配法まで一から説明するとかなり長くなるのでここでは割愛します。
なので、裏の理論としてはこういうことをしているのだ・・と理解しつつも、実際の計算はscikit-learnが出してくれるものを使っていけばOKです。
「(ⅲ)パラメータを出してみる」で$b$ = 4.950, $a_1$ = 446.180, $a_2$ = -400.540と出していますので、今回求めたかったのは$y = \frac{1}{1 + e^{-(446.180x_1 + (-400.540)x_2 + 4.950)}}$というシグモイド関数になります。
(ⅲ)ここでのまとめ
このシグモイド関数($y = \frac{1}{1 + e^{-(446.180x_1 + (-400.540)x_2 + 4.950)}}$)に新たに取得した生徒の国語点数($x_1$)と数学点数($x_2$)を入力すれば文系の確率が算出され、その確率が0.5より大きければ文系、0.5より小さければ理系と分類してくれるというわけです。
(ⅳ)やや発展
◆なぜLの最大値を求めれば”良さげな”パラメータが出せるのか
$L$、そして$logL$が最大になるようなパラメータ$a$や$b$を出しましたが、なぜ$L$や$logL$が最大になれば、最適なパラメータが出せるのでしょうか。
イメージをつかむために、下記をご覧ください。
あなたは手元に3つしかデータを持っておらず、そのたった3つのデータから、「全体の正規分布をざっくり青いグラフにしてみる」こととします。
下の2つの青いグラフのうち、どちらの方がより全体の正規分布である可能性が高そうでしょうか。
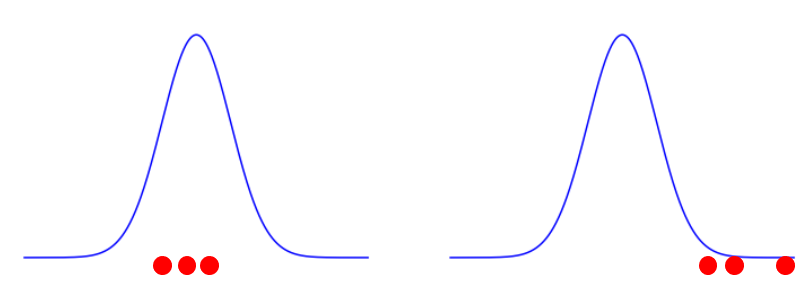
明らかに、左側のグラフの方が確からしい可能性が高いですね。なぜなら、右側の分布は一番発生頻度が高い山に、1つも手元のデータがないからです。
これは直感的な理解ですが、数学的にも左側のグラフの方が確からしさは大きいのです。
上の正規分布に、確率を付記したものが下記です。
目分量になりますが、手元にある赤い点がこの正規分布上ならこの確率で発生する・・という確率を書いてみました。
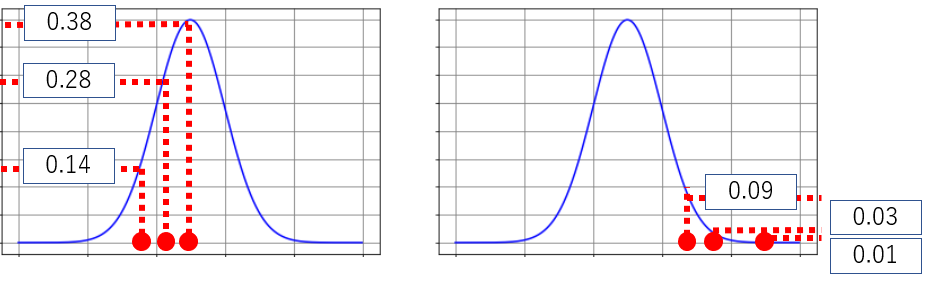
左の分布の確率を掛け算すると($L$と意味合いは同じことをしています)、0.14×0.28×0.38 = 0.014896 となります。
同様に右側は
0.01×0.03×0.09 = 0.000027 となります。
このように、確率の掛け算の値が大きくなればなるほど、本来の分布を適切に表しているグラフに近づくということです。
だから、文系の確率の掛け算である$L$やその対数の$logL$もその値がなるべく大きくなるようなパラメータ$a_1$、$a_2$、$b$を求めることが必要というわけです。
◆シグモイド関数とロジスティック関数の違い
ロジスティック関数の特殊形がシグモイド関数という理解でOK。
ロジスティック関数:$ {N={\frac {K}{1+\exp {K(t_{0}-t)}}}}N={\frac {K}{1+\exp {K(t_{0}-t)}}}$
シグモイド関数は上記の$K=1$,$t_0=0$とした場合の関数を指します。
参考URL:Wikipedia
https://ja.wikipedia.org/wiki/%E3%82%B7%E3%82%B0%E3%83%A2%E3%82%A4%E3%83%89%E9%96%A2%E6%95%B0
◆混同行列
今回は非常に分かりやすい例を出したので使いませんでしたが、一般には、精度の確認方法として混同行列という指標を使います。
参考URLを記載いたしますので、興味がある方は是非学習してみてください。
<参考URL>
https://note.nkmk.me/python-sklearn-confusion-matrix-score/
5.まとめ
いかがでしたでしょうか。
ロジスティック回帰は私自身非常に理解に苦しんだ部分なので、一度読んですんなり理解・・は難しいかもしれないです。
何度かお読みいただくことで、少しでも理解の進化の助けになりましたら幸いです。
※今後は他の機械学習モデルでも同じような投稿をしたいと思っております。