1.目的
機械学習をやってみたいと思った場合、scikit-learn等を使えば誰でも比較的手軽に実装できるようになってきています。
但し、仕事で成果を出そうとしたり、より自分のレベルを上げていくためには
「背景はよくわからないけど何かこの結果になりました」の説明では明らかに弱いことが分かると思います。
この記事では、**2~3で「理論はいいからまずはscikit-learn使ってみる」こと、4以降で「その背景を数学から理解する」**2つを目的としています。
※私は文系私立出身なので、数学に長けていません。可能な範囲で数学が苦手な方にもわかりやすいように説明するよう心がけました。
<2/5追記>
※ロジスティック回帰Verでも同様の記事を投稿していますので、併せてお読みいただけますと幸いです。
[【機械学習】ロジスティック回帰をscikit-learnと数学の両方から理解する]
(https://qiita.com/Hawaii/items/ee2a0687ca451fe213be)
<3/1追記>
・3.scikit-learnで線形回帰→(4)モデル構築→(ⅳ)補足を追加しました。
2. 線形(単)回帰とは
(1) 回帰とは
**数値を予測すること。**機械学習では、他に「分類」があるが、「●●円」「△Kg」といった数値を予測したい場合は、回帰を使うと考えればよい。
(2) 線形回帰とは
若干の語弊はあるかもしれないですが、
「求めたいもの($=y$)」と、「その求めたいものに影響を与えると思われるもの
($=x$)」に線形の関係がある場合、その線形の特徴を使って$y$を求めるやり方を線形回帰といいます。
分かりづらいと思うので、具体例を出します。
<具体例>
あなたは自営業でアイスクリーム屋さんを営んでおり、売上の目途を安定的に立てるため、**「自分の店のアイスクリームの売上を予測できるようになりたい」**と強く思っているとします。

あなたは、自分の店のアイスクリームの売上に影響を与えているのは何だろうかと必死に考え、気温が高いほどアイスクリームはたくさん売れ、気温が低いとアイスクリームは全然売れていないことに気が付きました。
そこで、下記のように「気温($=x$)」と「アイスクリームの売上($=y$)」の図示してみると、たしかに気温が上がればアイスクリームの売上が増える、そしてそこにはおおよそ直線の形(=$ax+b$)が引けそう(=線形である)だとわかります。

次から、scikit-learnを使って気温から、アイスクリームの売上を求める機械学習のモデルを構築してみましょう。
3.scikit-learnで線形回帰
(1)必要なライブラリのインポート
線形回帰を行うために必要な下記をインポートしておく。
from sklearn.linear_model import LinearRegression
(2)データの準備
気温とアイスクリームの売上を下記のようにdataとして設定する。
※例えば、下記でいうと気温が8°の日は売上が30万円、10°の日は売上が35万円となる。
data = pd.DataFrame({
"temprature(=x)":[8,10,6,15,12,16,20,13,24,26,12,18,19,16,20,23,26,28],
"sales(=y)":[30,35,28,38,35,40,60,34,63,65,38,40,41,43,42,55,65,69]
})
(3)図示してみる(重要)
気温とアイスクリームの売上について図示してみる。線形の関係にないと線形回帰を使っても、元のデータが線形でないため非常に精度が悪くなる。
いきなりscikit-learnを使うのではなく、どのようなデータでも図示することを心がけましょう。
plt.scatter(data["temprature(=x)"],data["sales(=y)"])
plt.xlabel("temprature(°)")
plt.ylabel("sales")
plt.grid(which='major',color='black',linestyle=':')

おおよそ、気温($=x$)と売上($=y$)に直線の関係がありそうなので、線形回帰のモデルを構築してみることにします。
(4)モデル構築
(ⅰ)データ整形
まずはモデル構築をするためにデータの形を整えていきます。
x = data["temprature(=x)"].values
y = data["sales(=y)"].values
X = x.reshape(-1,1)
今回はpython文法の記事ではないので詳細は割愛しますが、xとyをscikit-learnで線形回帰するための形に整えます。
※このあたりもある程度しっかりわかっていないと書けないコードだと思うので、どこかでまとめたいと思っています。
(ⅱ)モデル構築
いよいよ、モデル構築のコードです。
regr = LinearRegression(fit_intercept = True)
regr.fit(X,y)
拍子抜けしたかもしれないですが、単純なモデルであればこれで終わりです。
regrという変数にこれから線形回帰モデルを作ります!と宣言のようなことを行い、次の行で、そのregrに準備したXとyをフィット(=学習)させるというイメージです。
(ⅲ)直線の傾きと切片を出してみる
「2. 線形(単)回帰とは」(2)で記載しましたが、先ほどまでのscikit-learnで$y=ax+b$の$a$と$b$を求め、気温から売上を予測する直線の式を裏で求めています。
今のままだと実感がわかないので、実際に傾きを切片を出しておきましょう。
a = regr.coef_ #傾きを求める
b = regr.intercept_ #切片を求める
print(a)
print(b)
aが[1.92602996]、bが[12.226591760299613]と表示されると思います。
つまり、直線は$y(=売上)=1.92602996 * x(=気温) + 12.226591760299613$とscikit-learnが求めてくれたということです。
(ⅳ)補足
モデルを構築するだけであれば(ⅲ)までで事足りますが、他にも下記があります。
参考:https://pythondatascience.plavox.info/scikit-learn/%E7%B7%9A%E5%BD%A2%E5%9B%9E%E5%B8%B0
◆モデル構築で使用しているパラメータを表示
今回はfit_interceptをTrueにしているだけですが、他にも設定できるパラメータがあり、今それがどのように設定されているのか見ることができます。
regr.get_params()
そうすると{'copy_X': True, 'fit_intercept': True, 'n_jobs': None, 'normalize': False}と表示されます。
・copy_X:メモリ内でデータを複製してから実行するかどうかを選びます。 (デフォルト値: True)
・fit_intercept:False に設定すると切片(今回でいうと$b$)を求める計算を含めないため、目的変数が原点を必ず通る性質のデータを扱うときに利用します。 (デフォルト値: True)
・n_jbobs:計算に使うジョブの数。-1 に設定すると、すべての CPU を使って計算します。 (デフォルト値: 1)
・normalize:True に設定すると、説明変数を事前に正規化します。 (デフォルト値: False)
◆決定係数を表示
決定係数とは、0から1の範囲で、どれくらいそのモデルが実際のデータにフィットしているかを表す指標です。
regr.score(X,y)
◆誤差の評価
記述量が多くなるのであらためて記載はしませんが、下記が参考になります。
https://pythondatascience.plavox.info/scikit-learn/%E5%9B%9E%E5%B8%B0%E3%83%A2%E3%83%87%E3%83%AB%E3%81%AE%E8%A9%95%E4%BE%A1
(5)構築したモデルを図示してみる
それでは、この直線を先ほどの散布図に図示してみましょう。
# 直線の式
y_est_sklearn = regr.intercept_ + regr.coef_[0] * x
# 本来の気温と売上のプロット
plt.scatter(x, y, marker='o')
# 本来の気温と、予測の直線の式
plt.plot(x, y_est_sklearn, linestyle=':', color='green')
# 図の細かい設定
plt.grid(which='major',color='black',linestyle=':')
plt.grid(which='minor',color='black',linestyle=':')
plt.xlabel("temprature(°)")
plt.ylabel("sales")

このように、scikit-learnで何を出していて、どういうことにつながっているのかを意識するようにしましょう。
(6)現実世界では・・
モデルを作って終わり、では意味ないですね。現実世界では、この直線の予測モデルを使って、今後の売上を予測していくことが必要です。
あなたは今後の4日分の天気予報を見て、気温をメモしました。
それを下記のようにzという変数に格納します。
z = pd.DataFrame([10,25,24,22])
やりたいのは、先ほどscikit-learnで求めた直線の式に、上記の今後の気温予測をあてはめ、売り上げを予測することです。
regr.predict(z)
このようにすると、「([31.48689139, 60.37734082, 58.45131086, 54.59925094])」と結果が表示されます。
つまり、明日は気温10°なので売上は約31.5万円、明後日は気温25°なので売上は約60.3万円・・というかたちです。
むこう1か月分の気温の予測が取得できれば、売上のおおよその目途が立つということになり、あなたの目標は達成されます。
細かいことは他にも様々ありますが、まずはオーソドックスな線形回帰を実装してみるという点では良いのではないでしょうか。
4.線形(単)回帰を数学から理解する
さて、3まではscikit-learnを用いて$y=ax+b$の$a$と$b$を算出→図示→今後4日間の気温から売上を予測するという流れを実装してみました。
ここでは、この流れの「$y=ax+b$の$a$と$b$を算出」は、数学的にはどのように計算されているのかを明らかにしていきたいと思います。
※現状はこの知識は必要ないという方は読み飛ばしていただいて結構です。
(1)前提知識
a.基本的な微分
y = x^2 を xで微分すると y'=2x\\
y = x^2 + 4 をxで微分すると y'=2x\\
y = (-3x + 2)^2 をxで微分すると y' = 2(-3x +2)(-3)
b.Σ(シグマ)の意味
和を意味します
(2)数学的な理解
(ⅰ)y=ax+bのaとbを出すためにやっていること
前にも出した表を再掲します。
下記のように、気温と売上を予測するための「良い感じの直線」を引きたい、つまり傾きと切片のaとbを決めるのがやりたいことです。
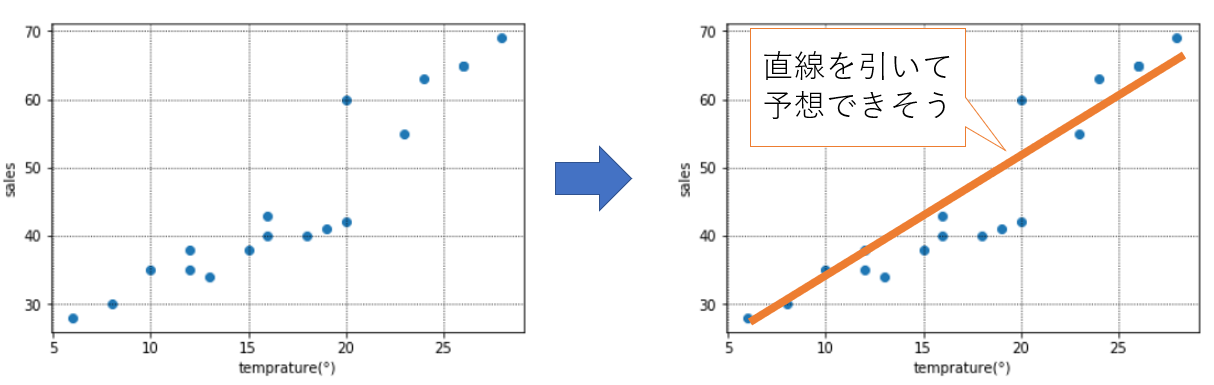
そのためには、aとbをどのように決めればいいでしょうか。
ここで、下の2つの直線を見てください。緑とオレンジで、どちらの方が気温と売上の関係をより精度高く予測できそうな直線でしょうか。
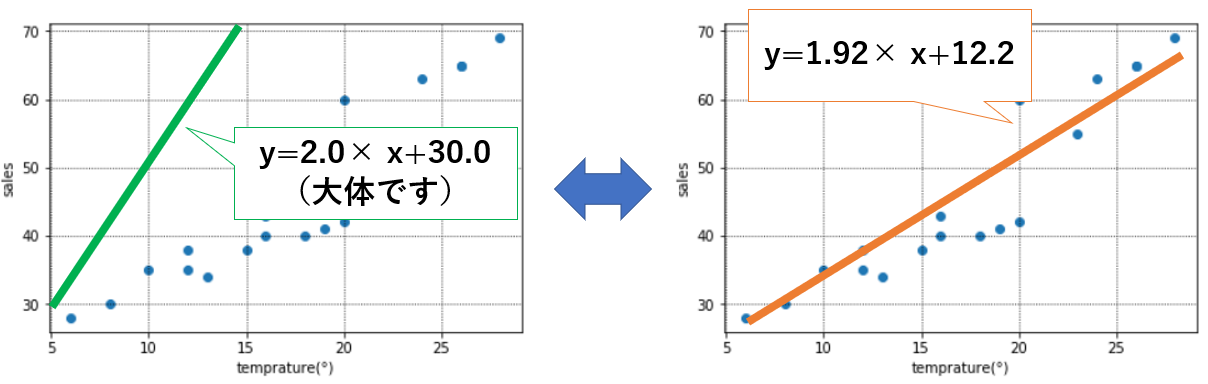
明らかに、オレンジ(a=1.92、b=12.2)の方が緑(a=2.0、b=30.0)より実際の気温と売上の関係を表せていそうなことが分かると思います。
それは**オレンジの直線の方が「直線と実際の青い点の距離がより近いから」**といえると思います。
つまり、scikit-learnでは、直線と青い点の距離が最も近くなるような「良いかんじの直線」になるようなaとbを求めているのです。
この、”直線と青い点の距離が最も近くなる”ようなaとbを求めるやり方を「最小二乗法」といいます。
(ⅱ)最小二乗法
もう少しかみ砕いていきましょう。
(ⅰ)で記載した「直線と青い点の距離」は、下記のように書くことができます。
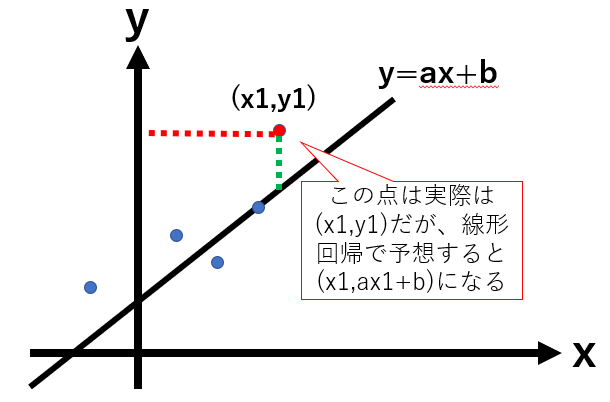
実際の座標(上の図の赤い点):$(x_1,y_1)$とすると、
$y=ax+b$で予測される座標:$(x_1,ax_1+b)$と表される。
この2つのy座標の誤差(=予測と実際の売上の差)は${y_1-(ax_1+b)}$と表せる。
※上の図の緑の距離を指す。
この${y_1-(ax_1+b)}$はあくまで赤い点1つの予測と実際の売上の誤差なので、これらをすべての点に対して合計し、この誤差がなるべく小さくなるようなaとbを求めていく(=なるべく予測と実際の差が小さくなるようなaとbを計算から求める)。
また、純粋に差を取るとプラスマイナスが打ち消されてしまうため、一般には誤差を2乗した数値をなるべく小さくなるように計算していく。この考え方を最小二乗法といいます。
※例えば、ある点では誤差が5、別の点では誤差が-5だったとする。この2つを足すと0になるが、別に誤差がなくぴったりの素晴らしい直線というわけではないことは想像できると思います。
このため、誤差の2乗、ここでいうと25と25を足して2乗誤差が50と考えます。
(ⅲ)最小二乗法を解いてみる
◆誤差関数の設定
全ての実際の点と直線から計算される予測値の誤差の和を仮に「E」とおくと、Eは下記のように表現できます。
※投稿が初心者なので{}のつけ方がわからず、[]で括ってしまいました・・すみません。
E = \sum_{i=1}^n [{y_i - (ax_i + b)}]^{2}
これは、実際の値$y_i$と予測値の$(ax_i + b)$の誤差の二乗を1つ目の点からn番目(実質すべて)まで足した数値を表します。
◆誤差関数を最小にするには
$E$の最小を考えるために、$E$の関数の形を表してみます。
※下記のグラフの形自体は正確なものではないので、イメージとしてとらえてください。
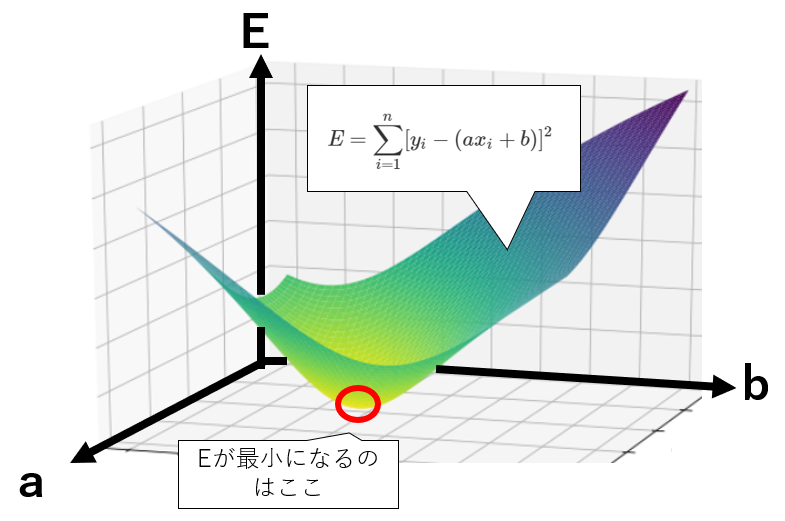
一般に$E$は上記のように表され、$E$が最小になるのは赤い点のあたりだと見てわかると思います。
では、この赤い点はどういう点かというと、「$E$を$a$で微分して0になり、かつ$E$を$b$で微分しても0になる」点です。
微分とは「傾き」を意味しているので、$a$の軸側から見て傾きが0になり、かつ$b$の軸側から見て傾きが0になる点が赤い点になります。
※突き詰めていくと凸最適化といった複雑な背景も入ってくるのでこれくらいの説明にとどめておきます。
◆実際に計算してみましょう
可能であれば、実際に紙とペンをご用意いただき、手を動かしてみてください。
【$a$で微分】
下記で使っている$∂$は微分するという意味で、「デル」と読みます(読み方はいくつかあります)。
\begin{align}
\frac{∂E}{∂a} &= \frac{∂}{∂a} \sum_{i=1}^n (y_i - ax_i - b)^{2}・・①\\
&= \sum_{i=1}^n 2*(y_i - ax_i - b)*(-x_i)・・②\\
&= \sum_{i=1}^n -2x_i(y_i - ax_i -b)・・③\\
&= \sum_{i=1}^n -2x_iy_i + \sum_{i=1}^n 2ax_i^2 + \sum_{i=1}^n 2x_ib・・④\\
\end{align}
・①を微分すると②になります(=なので、微分しますという意味の$∂$が②では消えています)
・③は②を若干式変形しただけで、④は③の各文字について$Σ$で分解しています。
$a$で微分して0になる点を探しているので、④=0として解いてみましょう。
\begin{align}
- \sum_{i=1}^n x_iy_i + a\sum_{i=1}^nx_i^2 + b \sum_{i=1}^n x_i = 0・・⑤\\
- \bar{xy} + a\bar{x^2} + b \bar{x} = 0・・⑥\\
\end{align}
⑤は、④=0なので、④の式についている係数の2を両辺で割った式です。
⑥は、⑤を両辺をnで割った式です。⑤は各$Σ$について、1番目からn個までデータを足しているので、nで割れば平均が出てきますよね。
もう少し具体的に話すと、1つ目の$Σ$の($-\sum_{i=1}^n x_iy_i$)は、$xy$を1番目からn番目までの総和です。つまりこれを$n$で割ってあげると、全体の平均になるので$- \bar{xy}$と表せるということです。
【$b$で微分】
同様に、$b$でも微分していきます。
\begin{align}
\frac{∂E}{∂b} &= \frac{∂}{∂b} \sum_{i=1}^n (y_i - ax_i - b)^{2}・・【1】\\
&= \sum_{i=1}^n 2*(y_i - ax_i - b)*(-1)・・【2】\\
&= \sum_{i=1}^n -2(y_i - ax_i -b)・・【3】\\
&= \sum_{i=1}^n-2y_i + \sum_{i=1}^n 2ax_i + \sum_{i=1}^n 2b・・【4】\\
\end{align}
【1】~【4】でやっていることは、$a$で微分している①~④と基本的に同じで、対応しています。
同様に⑤⑥と合わせて、【5】【6】も解いてみましょう。
\begin{align}
- \sum_{i=1}^ny_i + a\sum_{i=1}^nx_i + b = 0・・【5】\\
- \bar{y} + a\bar{x} + b = 0・・【6】\\
\end{align}
【連立方程式を解く】
⑥と【6】を、若干の式変形をして再掲します。
a\bar{x^2} + b \bar{x} = \bar{xy} ・・⑥'\\
a\bar{x} + b = \bar{y}・・【6'】
この2つの連立方程式を解くために(=$b$を消すために)【6'】に$\bar{x}$をかけてみましょう。
a\bar{x^2} + b \bar{x} = \bar{xy} ・・⑥'\\
a\bar{x}^2 + b\bar{x} = \bar{x}\bar{y}・・【6''】
間違いやすい注意点として、下記2つをおさえておきましょう。
・⑥'の「$a\bar{x^2}$」と【6''】の「$a\bar{x}^2$」は別物(⑥'は$x^2$の平均であるが【6''】は$\bar{x}$の二乗である)
・⑥'の「$\bar{xy}$」と【6''】の「$\bar{x}\bar{y}$」は別物(⑥'は$xy$の平均であるが、【6''】は$x$の平均と$y$の平均をかけている)
⑥-【6''】をすると下記のようになります。
a\bar{x^2} - a\bar{x}^2 = \bar{xy} - \bar{x}\bar{y}
これを$a$について解くと、
a = \frac{\bar{xy} - \bar{x}\bar{y}}{\bar{x^2} - \bar{x}^2}・・[A]
最後に、$b$について解きます。【6】から、$b = \bar{y} - a\bar{x}$なので[A]を代入すると、
b = \bar{y} - \frac{\bar{xy} - \bar{x}\bar{y}}{\bar{x^2} - \bar{x}^2}\bar{x}・・[B]
[A][B]より、求めたかった$a$と$b$が出せました。
◆求めたかった直線の式
ようやく$a$と$b$が出せたので、$E$を最小(=誤差が最小)にする「最もよさげな」直線の式は下記のように表現できます。
元々おいていた直線の式は$y = ax + b$なので、
y = \frac{\bar{xy} - \bar{x}\bar{y}}{\bar{x^2} - \bar{x}^2}x +( \bar{y} - \frac{\bar{xy} - \bar{x}\bar{y}}{\bar{x^2} - \bar{x}^2}\bar{x})
と表すことができました!
ポイントは、これを手で計算できたでしょ、すごいでしょということではなく、上記の式はすべて今手元にあるデータ(今回の例でいうと気温と売上のデータ)だけで計算できるという点です。
scikit-learnだと一発で計算してくれますが、裏ではこういう計算がされているのだということを背景として理解しておくことは非常に重要だと思います。
私は最初はここまでの一連の流れを理解するのに非常に時間がかかりました。最初は苦戦するかもしれないですが、皆さんも是非一緒に手を動かしていただけるといいのではと思います。
◆少し発展
手計算で算出した$y = \frac{\bar{xy} - \bar{x}\bar{y}}{\bar{x^2} - \bar{x}^2}x +( \bar{y} - \frac{\bar{xy} - \bar{x}\bar{y}}{\bar{x^2} - \bar{x}^2}\bar{x})$ですが、この中に出てくる一部の式では下記が成り立ちます。
<前提>
$\bar{xy} - \bar{x}\bar{y} = σ_{xy}$※共分散公式より
$\bar{x^2} - \bar{x}^2 = σ_x^2$ ※分散公式より
<結論>
y = \frac{σ_{xy}}{σ_x^2}x + (\bar{y} - \frac{σ_{xy}}{σ_x^2}\bar{x})
上記のように書き表すこともできます。
5.まとめ
以上、いかがでしたでしょうか。
私の思いとして、「最初からものすごい複雑なコードなんて見せられても自分で解釈できないから、精度は一旦どうでもいいのでまずはscikit-learn等で基本的な一連の流れを実装してみる」ことは非常に重要だと思っています。
ただ、慣れてきたらそれらを裏ではどのように動かしているのか、数学的な背景から理解していくことも非常に重要だと感じています。
とっつきづらい内容も多いと思いますが、少しでも理解の深化の助けとなりましたら幸いです。
※今後は重回帰やロジスティック回帰も同じような記事を投稿したいと思っております。
