【機械学習】決定木をscikit-learnと数学の両方から理解する

#1.目的
機械学習をやってみたいと思った場合、scikit-learn等を使えば誰でも比較的手軽に実装できるようになってきています。
但し、仕事で成果を出そうとしたり、より自分のレベルを上げていくためには
「背景はよくわからないけど何かこの結果になりました」の説明では明らかに弱いことが分かると思います。

この記事では、**２～３で「理論はいいからまずはscikit-learn使ってみる」こと、４以降で「その背景を数学から理解する」**２つを目的としています。

※私は文系私立出身なので、数学に長けていません。可能な範囲で数学が苦手な方にもわかりやすいように説明するよう心がけました。

※「数学から理解する」シリーズとして、同様の記事を投稿していますので、併せてお読みいただけますと幸いです。
【機械学習】線形単回帰をscikit-learnと数学の両方から理解する
[【機械学習】線形重回帰をscikit-learnと数学の両方から理解する]
(https://qiita.com/Hawaii/items/b84a0d669bcf5267e750)
[【機械学習】ロジスティック回帰をscikit-learnと数学の両方から理解する]
(https://qiita.com/Hawaii/items/ee2a0687ca451fe213be)
[【機械学習】SVMをscikit-learnと数学の両方から理解する]
(https://qiita.com/Hawaii/items/4688a50cffb2140f297d)
[【機械学習】相関係数はなぜ-1から1の範囲を取るのか、数学から理解する]
(https://qiita.com/Hawaii/items/3f4e91cf9b86676c202f)

※その他技術的な内容やデータサイエンスについてもブログを書いていますので、
よろしければこちらもご覧下さい。

[データサイエンス　はじめの一歩]
(https://hazimenoippo-hawaii.com/)

#2.　決定木とは

Wikipediaでは下記のように記載があります。

決定木は、意志決定を助けることを目的として作られる。 決定木は木構造の特別な形である。

言葉にするとちょっと難しいですが、ざくっと言うと「人の判断を木の構造のように細分化して、判断を進めていくモデル」です。

これもまだわかりづらいと思うので、具体例を出していきましょう。

###＜具体例＞
あなたは不動産屋さんだと仮定して、若い女性向けに選ばれやすい部屋・そうじゃない部屋をある程度事前に選別したいと考えています。
そこで、過去の13件のデータから、実際に若い女性から選ばれた部屋とそうでない部屋、そしてその部屋の情報を集めました。

	何階か	部屋の広さ$m^2$	オートロック	借りたら〇
物件1	4	30	有	〇
物件2	5	45	無	〇
物件3	3	32	有	〇
物件4	1	20	有	〇
物件5	6	35	有	〇
物件6	3	40	有	〇
物件7	4	38	有	〇
物件8	1	20	無	×
物件9	2	18	無	×
物件10	1	20	無	×
物件11	1	22	無	×
物件12	1	24	有	×
物件13	3	25	無	×

今回はわかりやすい例を出しましたが、確かに部屋を決めるとき、私たち自身も下記の様な考え方をするのではないでしょうか。

どの条件が一番上に来るかは人それぞれですが、例えば1階は少し嫌で、2階以上かをまずは考え、2階以上であれば、さらにオートロックもあればいいね、という意味で部屋を借りる。
逆に、2階以上じゃなくても（1階の部屋）、ある程度の部屋の広さならまあ借りてもいいか、逆に1階だし狭いなら借りないな・・・・というようなフローで考えていくと思います。

まさにこれが木の構造を表していて、このように条件を分岐させて判断を決めていくのが決定木です。

では、この条件の分岐はどのように決められるのでしょうか。今出した例は直感的な説明で、根拠も何もなかったと思います。

ここで出てくるのが「不純度」です。
詳細は後半の数学の章に回しますが、この不純度を元に決定木は条件の分岐を決めています。
要は、元のデータをなるべくきれいに（今回の例で言うと部屋を借りた・借りていないで）分けたい。この「きれいに」の指標が「不純度」です。

ちょっとよくわからないという人は、求めたい目的変数（今回では借りた・借りていない）をきれいに分類するために、決定木は不純度という指標を使って良い感じに枝分かれした木の構造の判断プロセスを作っていると考えていただければ大丈夫です。

#3.scikit-learnで決定木
##(1)必要なライブラリのインポート
決定木を行うために必要な下記をインポートしておく。
（その他にもnumpy等、インポートします）

import pandas as pd
import numpy as np
from sklearn.tree import DecisionTreeClassifier, export_graphviz
#下記は決定木可視化のためのツール
import graphviz
import pydotplus
from IPython.display import Image
from sklearn.externals.six import StringIO

##(2)データの準備
何階か、部屋の広さ、オートロックかという情報と部屋が借りられたか否かを下記のようにdataとして設定する（冒頭で出したデータの表と中身は同じです）。
※例えば、下記でいうと物件1は4階、部屋の広さは30$m^2$、オートロック有で、部屋は借りられたということです。

data = pd.DataFrame({
        "buy(y)":[True,True,True,True,True,True,True,False,False,False,False,False,False],
        "high":[4, 5, 3, 1, 6, 3, 4, 1, 2, 1, 1,1,3],
        "size":[30, 45, 32, 20, 35, 40, 38, 20, 18, 20, 22,24,25],
        "autolock":[1, 0, 1, 1, 1, 1, 1, 0, 0, 0, 0,1,0]
    })

##(3)モデル構築
####(ⅰ)データ整形
まずはモデル構築をするためにデータの形を整えていきます。

y = data.loc[:,["buy(y)"]]
X = data.loc[:,["high", "size","autolock"]]

今回はpython文法の記事ではないので詳細は割愛しますが、Xとyをscikit-learnで決定木するための形に整えます。
※このあたりもある程度しっかりわかっていないと書けないコードだと思うので、どこかでまとめたいと思っています。

####(ⅱ)モデル構築
いよいよ、モデル構築のコードです。

clf = DecisionTreeClassifier()
clf = clf.fit(X, y)

単純なモデルであればこれで終わりです。
clfという変数にこれから決定木モデルを作ります！と宣言のようなことを行い、次の行で、そのclfに準備したXとyをフィット(=学習)させるというイメージです。

##(3)モデル可視化

###◆可視化コード
単純なモデルであれば(2)までで終わりですが、決定木の長所の１つに、「可読性の高さ」があります。簡単に言うと、「そのモデルでどうしてこの結果になったのか、機械学習をあまり知らない人にでもわかりやすい」ということです。

木構造の判断プロセスを可視化してみましょう。

dot_data = StringIO() #dotファイル情報の格納先
export_graphviz(clf, out_file=dot_data,  
                     feature_names=["high", "size","autolock"],#編集するのはここ  
                     class_names=["False","True"],#編集するのはここ（なぜFase,Trueの順番なのかは後程触れます）  
                     filled=True, rounded=True,  
                     special_characters=True) 
graph = pydotplus.graph_from_dot_data(dot_data.getvalue()) 
Image(graph.create_png())

上記のコードを実行すると、下記の様な図が表示されます。

###◆分岐の見方
上記で可視化できました！で終わっている記事やサイトが多いですが、私はこの図の見方が分からず、最初苦労しましたので、簡単に見方も加えておきます。
※gini係数や不純度という言葉が出てきますが、詳しくは数学の章で扱います。

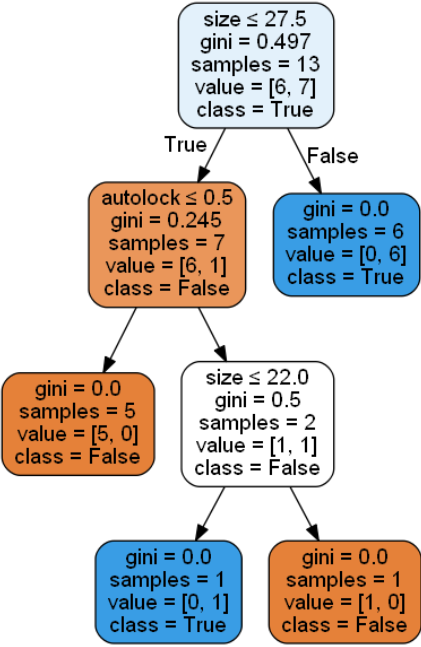
(a)一番上の薄水色の箱
これは一番最初の状態です。gini以下が現在の状態を示しています。
ーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーー
gini係数：0.497
sample（データ数）：13
value：6個と7個にデータが分かれていて、多い方のTrueがclassとして表示されています。
ーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーー
※valueの並び順について
今回はデータが少ないので7個の方がTrueだなとわかりますが、データが多い場合、valueとして数が表示されていても、どちらがどっちの（今回で言うとTrueがFalse）データかわからないと思います。
その時は、下記のように記述します。

clf = DecisionTreeClassifier()#ここはさっきと同じ
clf = clf.fit(X, y)#ここはさっきと同じ
print(clf.classes_)#ここを追加

そうすると、今回であれば[False,True]と表示されます。つまり、valueの並びはFalse,Trueの順番であることが分かるというわけです。

これが、可視化コードでclass_names=["False","True"],#編集するのはここ（なぜFase,Trueの順番なのかは後程触れます）と記載した理由です。
DecisionTreeClassifier()で順番がFalse,Trueの順になっているので、class_namesも同じ順番にしてあげないと、可視化した際に実際と逆の名前をつけてしまうことになるので要注意です。（私はここでかなり躓きました）

(b)２行目、右の青色の箱
最初の分岐でsize（部屋の広さ）が27.5$m^2$以下ではない（=27.5$m^2$以上である）場合を指しており、その時はgini係数0、sample（データ数）6、Trueが6個に分かれます。

つまり、部屋の広さが27.5$m^2$以上である場合、必ずその部屋は借りられるということを表しています！gini係数が0、つまり不純度が0になったのでこれ以上は分岐はされず、ここで終わりです。

以下、他の分岐も同じようにみていけばわかると思います。
※補足ですが、autolockのように0,1の2値設定をしたものは、分岐条件を見ればわかりますが0.5以下（or以上）か否かが条件になっています。これは0.5以上ということはつまり1（今回であればオートロック有）、0.5以下ということはつまり0（オートロック無）を示しています。

ここまでで決定木をscikit-learnで実装することと、可視化の流れが終わりです。

##(4)現実世界では・・
モデルを作って終わり、では意味ないですね。現実世界では、この予測モデルを使って、今後新しい部屋のデータを得た際にその部屋は借りられるか否かを予測していくことが必要です。
あなたは新しい部屋の２つ分のデータをメモしました。
それを下記のように変数に格納します。

z = pd.DataFrame({
        "high":[2, 3],
        "size":[25, 18],
        "autolock":[1,0]
    })
z2 = z[["high", "size","autolock"]].values

やりたいのは、先ほどscikit-learnで構築した決定木モデル（clf）に、上記の追加データをあてはめ、その部屋は借りられそうか否かを予測することです。

y_est = clf.predict(z2)
y_est

このようにすると、「([False,False])」と結果が表示されます。つまり、残念ながらこの２部屋は借りられない可能性が高そうなので、若い女性以外のターゲット層に営業するといった戦略を取る必要性があると考えられます。

細かいことは他にも様々ありますが、まずはオーソドックスな決定木を実装してみるという点では良いのではないでしょうか。

#4.決定木を数学から理解する
さて、３まではscikit-learnを用いて決定木モデルを構築→可視化→新しいデータを用いて予測という流れを実装してみました。
ここでは、この流れの決定木モデルは、数学的にはどのように計算されているのかを明らかにしていきたいと思います。
※現状はこの知識は必要ないという方は読み飛ばしていただいて結構です。

そのためには、前半で紹介した「不純度」と「情報量」、不純度を測る指標として「エントロピー」「ジニ係数」の話が必要です。

###(ⅰ)不純度
前半で、決定木は不純度を元に判断プロセスを構築していくと記載しました。
もう少しだけ細かく書くと、不純度は**「データがどれだけばらついているかを表す指標」**です。

例えば分類では、完全に分類できれば不純度は０になりますし、回帰では１つのノード内でのデータの分散が０であれば不純度は０になります。

ですので、決定木はこの不純度をなるべく小さく（０に近く）できるようにしています。
この不純度を測る指標として「エントロピー」「ジニ係数」があります。その説明に入るために、情報量について次で扱います。

###(ⅱ)情報量
ここでは、情報量の考え方をざっくりおさえようと思います。
情報量とは、**「その事象を知った際の驚き度合いを数値化した指標」**です。

例えば、あなたは友達と話していて、下記を聞きました。どちらがより驚くでしょうか。

１つ目：明日、沖縄は晴れるらしいよ。
２つ目：フィギュアスケートの羽生君って、実はラグビーもプロ並みにすごいらしいよ。（あくまで、空想の話です）

明らかに２つ目の話の方が驚きますよね。なぜなら、２つ目の話って到底起きそうにない事象の情報を得たからです。
このケースでは、２つ目の方が情報量多いと言えます。

この情報量は、情報理論の世界では下記のように定義されています。

I(x) = -\log_{2} P(x)

※$I(x)$は事象$x$の情報量（単位はbits）
※$P(x)$はある事象が起きる確率

先ほどのケースで、例えば沖縄が晴れる確率が0.8、羽生君が実はラグビーもプロ並みにすごい確率を0.01とすると、情報量は下記のように計算できます。

沖縄が晴れる事象の情報量：$-\log_{2} 0.8 = 0.322$
羽生君の事象の情報量：$-\log_{2} 0.01 = 6.644$

羽生君の事象の情報量が圧倒的に大きいですね！

※参考※
$\log$の計算は下記サイトのWolframAlphaで簡単に計算できます。
（上に出てくるバーに、「-log2(0.8)」と入力すれば値が返ってきます）
https://www.wolframalpha.com/

ここまでは情報量の説明をしてきました。この内容を受け、エントロピーの話に進みましょう。

###(ⅲ)エントロピー
####◆エントロピーについて
エントロピーは(ⅰ)の情報量を平均化した指標で、情報量のばらつき具合を示します。

大半は同じ事象が何回も観測される場合、エントロピーが小さいです。
一方で、観測するたびに異なる事象が発生する場合は、エントロピーが大きいです。

例えば先ほどのような沖縄の天気は晴れがいつも多いので、エントロピーが小さいです。
一方で、関東の天気はいつも晴れではなく、曇りも雨も多いので、エントロピーが大きいと言えます。

エントロピーは下記のように定義されています。

H = \sum_{i=1}P(x_i)I(x_i) = -\sum_{i=1}P(x_i)\log_{2}P(x_i)

※$H$はエントロピー、$I(x_i)$はある事象$x_i$に対する情報量を指す

先ほどのケースで、例えば沖縄が晴れる確率を0.8、曇りの確率が0.05、雨の確率が0.15とします。そして、関東が晴れる確率を0.6、曇りの確率が0.2、雨の確率が0.2とするとそれぞれのエントロピーは下記のように計算できます。

沖縄の天気のエントロピー：0.884
※先ほどのWolframAlphaに下記を入力してください。
80/100(log2(0.8)) +5/100(log2(0.05)) + 15/100(log2(0.15))

関東の天気のエントロピー：0.953
※先ほどのWolframAlphaに下記を入力してください。
60/100(log2(0.6)) +20/100(log2(0.2)) + 20/100(log2(0.2))

関東の天気のエントロピーの方が大きいので、情報量がばらついていることがわかります。

####◆エントロピーと不純度の関係について
決定木は不純度をなるべく小さくするようにしていると記載しました。
エントロピーと不純度の関係としては、不純度が最も低ければエントロピーは０、不純度が高くなるほどエントロピーは大きくなります。

不純度はデータのばらつき具合を示すものでしたし、エントロピーも情報量のばらつき具合を示していたので、直感的に納得しやすいのではないでしょうか。

####◆決定木とエントロピーについて
では、決定木においてエントロピーは具体的にどのように計算され、モデルは構築されていくのでしょうか。

それは、分岐前のエントロピーと分岐後のエントロピーの差を計算し、その差が最も大きくなるような分岐条件を探し、モデルを構築しているのです。

言葉で書くと長ったらしくなりますが、要は、決定木を良いモデルにするためにはデータのばらつきである不純度をなるべく小さくしたい、つまりエントロピーも小さくしたい。

そのためには、１つ前の分岐より次の分岐をした後のエントロピーがより小さくなる、つまり分岐前のエントロピーと分岐後のエントロピーの差がなるべく大きくなるような分岐条件を探せばいいということになりますね。

###(ⅳ)ジニ係数
####◆ジニ係数について
不純度を測る指標として、エントロピーの他にジニ係数があります。
ジニ係数とは誤分類する確率を平均化した指標のことです。

もう少し詳しく書きますと、あるノード$t$においてクラス$x_i$が選ばれる確率を$P(X_i \mid t)$とすると、ジニ係数はあるノードにおいて誤分類する確率の期待値として定義されます。つまり、誤分類をどれくらいしてしまいそうかの指標になります。

ジニ係数は下記のように定義されます。

G(t) = \sum_{i=1}^{K}P(x_i \mid t)\left(1-P(x_i \mid t)\right) = 1-\sum_{i=1}^{K}P(x_i \mid t)^2

※$G$はジニ係数、$K$はクラス数、$P(x_i \mid t)$はあるノード$t$においてクラス$x_i$が選ばれる確率です。

####◆ジニ係数と不純度の関係について
決定木は不純度をなるべく小さくするようにしていると記載しました。
ジニ係数と不純度の関係としては、不純度が最も低ければエントロピーは０、不純度が高くなるほどエントロピーは大きくなります（最大1）。

####◆決定木とジニ係数について
この範囲は、上記の「◆決定木とエントロピーについて」と考え方は同じなので割愛します。分岐前のジニ係数と分岐後のジニ係数の差がなるべく大きくなるような条件分岐を構築します。

###(ⅴ)まとめ
以上のように、決定木は木の構造の様な判断プロセスを構築するモデルで、その判断基準はデータのばらつきを表す「不純度」をなるべく小さくすることでした。

その不純度を測る指標は「事象のばらつき具合を示すエントロピー」「誤分類をどれくらいしてしまいそうかを示すジニ係数」があり、どぢらも、分岐前と分岐後の差が最も大きくなるような分岐条件を設定している、というのが決定木が裏でしていることでした。

そして、エントロピーやジニ係数の具体的な計算式も見ていきました。

※補足※
実際にpythonでモデルを動かす際は、3で紹介したコードに引数として下記のように設定できます（下記は不純度の指標をジニ係数にした場合。エントロピーにしたい場合はここをentropyにします）。

clf = DecisionTreeClassifier(criterion="gini")
clf = clf.fit(X, y)

#5.結び
以上、いかがでしたでしょうか。
私の思いとして、「最初からものすごい複雑なコードなんて見せられても自分で解釈できないから、精度は一旦どうでもいいのでまずはscikit-learn等で基本的な一連の流れを実装してみる」ことは非常に重要だと思っています。

ただ、慣れてきたらそれらを裏ではどのように動かしているのか、数学的な背景から理解していくことも非常に重要だと感じています。

とっつきづらい内容も多いと思いますが、少しでも理解の深化の助けとなりましたら幸いです。

※その他技術的な内容やデータサイエンス、勉強法についてもブログを書いていますので、よろしければこちらもご覧下さい。

[データサイエンス　はじめの一歩]
(https://hazimenoippo-hawaii.com/)