【機械学習】線形重回帰をscikit-learnと数学の両方から理解する

#1.目的
機械学習をやってみたいと思った場合、scikit-learn等を使えば誰でも比較的手軽に実装できるようになってきています。
但し、仕事で成果を出そうとしたり、より自分のレベルを上げていくためには
「背景はよくわからないけど何かこの結果になりました」の説明では明らかに弱いことが分かると思います。

この記事では、**２～３で「理論はいいからまずはscikit-learn使ってみる」こと、４以降で「その背景を数学から理解する」**２つを目的としています。

※私は文系私立出身なので、数学に長けていません。可能な範囲で数学が苦手な方にもわかりやすいように説明するよう心がけました。
（とはいえ、今回は線形代数の知識が必要になるので、難しいと感じる方は、そういうものか、と受け流すくらいで大丈夫です。）

※「数学から理解する」シリーズとして、同様の記事を投稿していますので、併せてお読みいただけますと幸いです。
【機械学習】線形単回帰をscikit-learnと数学の両方から理解する
[【機械学習】ロジスティック回帰をscikit-learnと数学の両方から理解する]
(https://qiita.com/Hawaii/items/ee2a0687ca451fe213be)
[【機械学習】SVMをscikit-learnと数学の両方から理解する]
(https://qiita.com/Hawaii/items/4688a50cffb2140f297d)
[【機械学習】相関係数はなぜ-1から1の範囲を取るのか、数学から理解する]
(https://qiita.com/Hawaii/items/3f4e91cf9b86676c202f)

#2.　線形（重）回帰とは
上記の、線形単回帰とも重複する箇所がありますので線形単回帰の記事も併せて参考にしてください。
【機械学習】線形単回帰をscikit-learnと数学の両方から理解する
##(1)　回帰とは
**数値を予測すること。**機械学習では、他に「分類」があるが、「●●円」「△Kg」といった数値を予測したい場合は、回帰を使うと考えればよい。

##(2)　線形回帰とは
若干の語弊はあるかもしれないですが、
「求めたいもの($=y$)」と、「その求めたいものに影響を与えると思われるもの
($=x$)」に線形の関係がある場合、その線形の特徴を使って$y$を求めるやり方を線形回帰といいます。

線形単回帰は$x$は1つでしたが、線形重回帰は$x$が複数あります。

分かりづらいと思うので、具体例を出します。
＜具体例＞
あなたは自営業でアイスクリーム屋さんを営んでおり、売上の目途を安定的に立てるため、**「自分の店のアイスクリームの売上を予測できるようになりたい」**と強く思っているとします。

あなたは、自分の店のアイスクリームの売上に影響を与えているのは何だろうかと必死に考えました。
線形単回帰の記事では、アイスクリームの売上に影響を与えているのは「気温」と仮定して話を進めてきましたが、よく考えると、あなたが本当にアイスクリーム屋さんを営んでいたとしたら、売上に影響を与えているのは本当に「気温だけ」という結論をたてるでしょうか。

おそらく、気温だけでなく、その日のアイスクリーム屋さんの通りの交通量や、それこそ、一緒に働く従業員の影響も大きいと考えるのではないでしょうか。
このように、通常は目的変数（アイスクリームの売上）に影響を与えると思われる説明変数は複数あり、場合によっては数万個ある、という場合もあります。

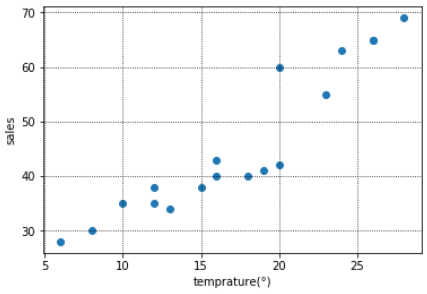
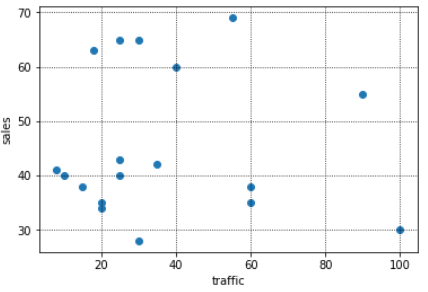
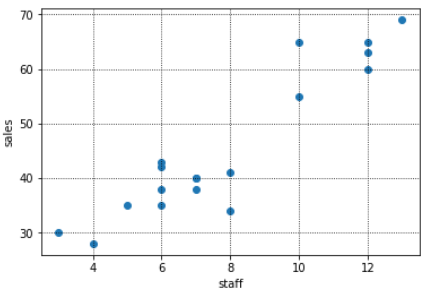
そこで、下記のように「いくつかの説明変数($=x$)」と「目的変数(アイスクリームの売上($=y$))」を図示してみると、説明変数と目的変数（アイスクリームの売上）にはおおよそ直線の形(=$ax+b$)が引けそう(=線形である）なものや、あまり関係なさそうなものがあることがわかります。

＜売上と気温の散布図＞

＜売上と交通量の散布図＞

＜売上とその日にシフトに入っていた従業員数の散布図＞

このように図示すると、売上と線形の関係にありそうな「気温」と「従業員数」を説明変数に使用し、「交通量」は使わないという選択もできます。
ここでは、後の例として使うので、「交通量」も説明変数に入れていきます。

次から、scikit-learnを使って気温・交通量・従業員数から、アイスクリームの売上を求める機械学習のモデルを構築してみましょう。

#3.scikit-learnで線形回帰
##(1)必要なライブラリのインポート
線形回帰を行うために必要な下記をインポートしておく。

import numpy as np
import pandas as pd
from sklearn.linear_model import LinearRegression

##(2)データの準備
気温、交通量、従業員数とアイスクリームの売上を下記のようにdataとして設定する。
※例えば、下記でいうと気温が8°の日は売上が30万円、10°の日は売上が35万円となる。

data = pd.DataFrame({
    "temprature":[8,10,6,15,12,16,20,13,24,26,12,18,19,16,20,23,26,28],
    "car":[100,20,30,15,60,25,40,20,18,30,60,10,8,25,35,90,25,55],
    "clerk":[3,5,4,6,6,7,12,8,12,10,7,7,8,6,6,10,12,13],
    "sales(=y)":[30,35,28,38,35,40,60,34,63,65,38,40,41,43,42,55,65,69]
    })

##(3)モデル構築
####(ⅰ)データ整形
まずはモデル構築をするためにデータの形を整えていきます。

y = data["sales(=y)"].values
X = data.drop("sales(=y)", axis=1).values  #sales以外の列をXとして定義する、という意味

今回はpython文法の記事ではないので詳細は割愛しますが、Xとyをscikit-learnで線形回帰するための形に整えます。
※このあたりもある程度しっかりわかっていないと書けないコードだと思うので、どこかでまとめたいと思っています。

####(ⅱ)モデル構築
いよいよ、モデル構築のコードです。

regr = LinearRegression(fit_intercept = True)
regr.fit(X,y)

単純なモデルであればこれで終わりです。
regrという変数にこれから線形回帰モデルを作ります！と宣言のようなことを行い、次の行で、そのregrに準備したXとyをフィット(=学習)させるというイメージです。

####(ⅲ)直線の傾きと切片を出してみる
「2.　線形（重）回帰とは」(2)で記載しましたが、先ほどまでのscikit-learnで$y=a_1x_1+ a_2x_2 + a_3x_3 + b$の$a$と$b$を求め、気温、交通量、従業員数から売上を予測する直線の式を裏で求めています。
今のままだと実感がわかないので、実際に傾きと切片を出しておきましょう。

b = regr.intercept_
a1 = regr.coef_[0]
a2 = regr.coef_[1]
a3 = regr.coef_[2]

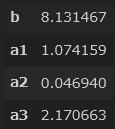
pd.DataFrame([b,a1,a2,a3],index = ["b","a1","a2","a3"])

すると、下記のように表示されます。

つまり、今回の線形回帰の式は、$y = 1.074159x_1 + 0.04694x_2 + 2.170663x_3 + 8.131467$で求められることが分かります。

補足になりますが、最初の図示で売上とあまり関係なさそうだった交通量($x_2$)の係数($=a_2$)は0.04694と、他2つの係数に比べて非常に小さいことが、計算からもわかりますね。つまり、交通量は$y$を求める際にあまり影響を与えない(=重要でない)変数であることが、あらためてわかります。

##(6)現実世界では・・
モデルを作って終わり、では意味ないですね。現実世界では、この予測モデルを使って、今後の売上を予測していくことが必要です。
あなたは今後の3日分の気温、見込み交通量、従業員数をメモしました。
それを下記のようにzという変数に格納します。

z = pd.DataFrame([[20,15,18],
                  [15,60,30],
                  [5,8,12]])

やりたいのは、先ほどscikit-learnで求めた直線の式に、上記の今後のデータをあてはめ、売り上げを予測することです。

regr.predict(z)

このようにすると、「([69.39068087, 92.18012508, 39.92573722])」と結果が表示されます。
つまり、明日の売上は約69.4万円、明後日は約92.2万円・・というかたちです。
むこう１か月分のデータが取得できれば、売上のおおよその目途が立つということになり、あなたの目標は達成されます。

細かいことは他にも様々ありますが、まずはオーソドックスな線形回帰を実装してみるという点では良いのではないでしょうか。

#4.線形(重)回帰を数学から理解する
さて、３まではscikit-learnを用いて$y=a_1x_1+ a_2x_2 + ・・・+ a_ix_i +b$の$a$と$b$を算出→今後3日間のデータから売上を予測するという流れを実装してみました。
ここでは、この流れの「$a$と$b$を算出」は、数学的にはどのように計算されているのかを明らかにしていきたいと思います。
※現状はこの知識は必要ないという方は読み飛ばしていただいて結構です。
※今回はベクトル、線形代数が登場してきますので、難しいと感じる方は、「そういうものなのだ」と思っていただく程度で大丈夫です。

##(1)前提知識（基本的なベクトル、線形代数）

$\frac{∂c}{∂\boldsymbol{x}} = 0 ←定数をxで微分すると0になる$

$\frac{∂(\boldsymbol{c}^T\boldsymbol{x})}{∂\boldsymbol{x}} = \boldsymbol{c}$

$\frac{∂(\boldsymbol{x}^TC\boldsymbol{x})}{∂\boldsymbol{x}} = (C

• C^T)\boldsymbol{x}$

##(2)数学的な理解

####(ⅰ)重回帰分析の式について

◆重回帰分析の式
前半でも触れましたが、重回帰分析の式は一般に下記のように表されます。

$\hat{y} = a_1x_1 + a_2x_2 + ・・ + a_mx_m + a_0・1$

※$a_0・1$は、いわゆる$y = ax + b$でいう$b$のことを指していて、定数の何らかの数値として設定しています。
※今回は詳細は割愛しますが、$a_0・1$はデータ全体を標準化すれば0になります。今回は標準化はしないですが、通常は標準化することも多いので、$a_0・1$を解析的に求めることはしていません。

◆今回の例で言うと・・
$x_1$が気温、$x_2$が交通量、$x_3$が従業員数で、それぞれの数値に何らかの係数$a_1,a_2,a_3$を掛けて、最後に定数$a_0・1$を足して売上$\hat{y}$を求めています。

####(ⅱ)重回帰分析の式をベクトルで表現する

(ⅰ)の重回帰分析の式の$x$をベクトル$x$、すなわち$\boldsymbol{x}$として表すと下記のようになります。

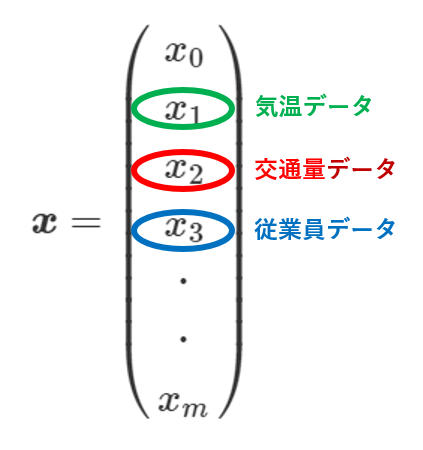
今回は説明変数が３つなので$x_3$までになりますが、一般には上記のように表します。

そして、例えば上記の$x_1$の気温データも、データは1つではなく、その中には複数日程分の気温データが格納されているはずです。
それを行列$X$で表しているのが下記です。

同様にベクトル$a$、すなわち$\boldsymbol{a}$は下記のように表せます。

$
\boldsymbol{a} = \begin{pmatrix}
a_0\
a_1\
a_2\
a_3\
・\
・\
a_m
\end{pmatrix}
$

つまり、元の売上を予測する重回帰分析の式が$\hat{y} = a_1x_1 + a_2x_2 + ・・ + a_mx_m + a_0・1$なので、$\hat{y} = \boldsymbol{X}\boldsymbol{a}$と表すことができます。

重要なことは、$\hat{y}$と$\boldsymbol{X}$は自分の手元にあるデータからわかるので、これらを代入して$\boldsymbol{a}$、すなわち重回帰分析の式の各説明変数の係数が計算できるということです。

次から、この式を用いて$\boldsymbol{a}$を解析的(=手計算)に求めていきましょう。
Scikit-learnが裏で行っているのも、これと同じ計算です。（厳密には異なるのですが、後程触れます。）

####(ⅲ)誤差関数の計算
線形単回帰の記事でも触れていますが、$\hat{y} = a_1x_1 + a_2x_2 + ・・ + a_mx_m + a_0・1$の$a_1$や$a_2$、$a_3$を決めるには、本当の売上$y$と、あくまで予測値の$\hat{y}$の差がなるべく小さくなるように、良さげな$a_1,a_2,a_3$を設定します。

「良さげな」とはどういうことか、$y$と$\hat{y}$の差（誤差関数）を計算しながら見ていきましょう。

$\begin{align}
E &=
\sum_{i=1}^n ({y_i - \hat{y}})^{2}\
&= (y - \hat{y})^T(y - \hat{y})\
&= (y - \boldsymbol{X}\boldsymbol{a})^T(y - \boldsymbol{X}\boldsymbol{a}) ←\hat{y}に\boldsymbol{X}\boldsymbol{a}を代入\
&= (y^T - (\boldsymbol{X}\boldsymbol{a})^T)(y - \boldsymbol{X}\boldsymbol{a})\
&= (y^T - a^T\boldsymbol{X}^T)(y - \boldsymbol{X}\boldsymbol{a})←(\boldsymbol{X}\boldsymbol{a})^T = a^T\boldsymbol{X}^T\
&= y^Ty - y^T\boldsymbol{X}\boldsymbol{a} - a^T\boldsymbol{X}^Ty + a^T\boldsymbol{X}^T\boldsymbol{X}\boldsymbol{a}←1つ上の式を展開\
&= y^Ty - 2y^T\boldsymbol{X}\boldsymbol{a} + a^T\boldsymbol{X}^T\boldsymbol{X}\boldsymbol{a}←a^T\boldsymbol{X}^Ty = y^T\boldsymbol{X}\boldsymbol{a}より
\end{align}$

この$E$を最小にするために、$E$を$\boldsymbol{a}$で微分し、0になる$\boldsymbol{a}$を求めます。
（なぜ微分して0になるようにするのかは、線形単回帰の記事を参照してください）

$
\begin{align}
\frac{∂E}{∂\boldsymbol{a}} &= \frac{∂}{∂\boldsymbol{a}}(y^Ty) - 2\frac{∂}{∂\boldsymbol{a}}(y^T\boldsymbol{X}\boldsymbol{a}) + \frac{∂}{∂\boldsymbol{a}}(a^T\boldsymbol{X}^T\boldsymbol{X}\boldsymbol{a})←\frac{∂}{∂\boldsymbol{a}}(y^Ty)は0になる\
&= -2\boldsymbol{X}^Ty + [\boldsymbol{X}^T\boldsymbol{X} + (\boldsymbol{X}^T\boldsymbol{X})^T]\boldsymbol{a}←前提知識の3つ目の式のCはここでいうと\boldsymbol{X}^T\boldsymbol{X}にあたる\
&= -2\boldsymbol{X}^Ty + 2\boldsymbol{X}^T\boldsymbol{X}\boldsymbol{a}
\end{align}
$

この誤差関数が0になるから、

$
\begin{align}
-2\boldsymbol{X}^Ty + 2\boldsymbol{X}^T\boldsymbol{X}\boldsymbol{a} = 0\
2\boldsymbol{X}^T\boldsymbol{X}\boldsymbol{a} = 2\boldsymbol{X}^Ty\
\boldsymbol{X}^T\boldsymbol{X}\boldsymbol{a} = \boldsymbol{X}^Ty\
\end{align}
$

つまり、求めたかった$\boldsymbol{a}$は下記のように求められます。

$\boldsymbol{a} = (\boldsymbol{X}^T\boldsymbol{X})^{-1} \boldsymbol{X}^Ty$

##(3)発展～pythonで実装してみる～
求めたかった$\boldsymbol{a}$は数式で表現できましたが、これだけ提示されても、重回帰はいまいちぴんとこないかもしれないです（私はきませんでした）。

そこで、ここでは、pythonのnumpyを使って、上記の式から解析的に重回帰分析の式を算出してみたいと思います。

◆データセット

(ⅰ)numpyのインポート

import numpy as np

(ⅱ)データセット
少し見づらいかもしれないですが、xの左の縦1列が気温、2列目が交通量、3列目が従業員数です。yは売上です。

x = np.matrix([[8,100,3],
              [10,20,5],
              [6,30,4],
              [15,15,6],
              [12,60,6],
              [16,25,7],
              [20,40,12],
              [13,20,8],
              [24,18,12],
              [26,30,10],
              [12,60,7],
              [18,10,7],
              [19,8,8],
              [16,25,6],
              [20,35,6],
              [23,90,10],
              [26,25,12],
              [28,55,13]])
y = np.matrix([[30],
              [35],
              [28],
              [38],
              [35],
              [40],
              [60],
              [34],
              [63],
              [65],
              [38],
              [40],
              [41],
              [43],
              [42],
              [55],
              [65],
              [69]])

(ⅲ)重回帰分析
先ほど示した通り、$\boldsymbol{a} = (\boldsymbol{X}^T\boldsymbol{X})^{-1} \boldsymbol{X}^Ty$なので、下記のように記述します。

(x.T * x)**-1 * x.T * y

そうすると、このように結果が表示されます。つまり、numpy上で計算すると$a_1 = 1.26, a_2 = 0.09, a_3 = 2.47$ということになります。
matrix([[1.26664688],
[0.09371714],
[2.47439799]])

これは、scikit-learnで求めた$a_1,a_2,a_3$と数値が微妙に異なりますが、scikit-learnはこのnumpyの計算に、さらにバイアス（というもの）を考慮しているためです。
そこまで突っ込み始めるとより複雑になってくるので、scikit-learnが裏で行っている基本的な計算を知るという意味では、まずは今回レベルのことを押さえておければいいのではと思います。

#5.まとめ
以上、いかがでしたでしょうか。
私の思いとして、「最初からものすごい複雑なコードなんて見せられても自分で解釈できないから、精度は一旦どうでもいいのでまずはscikit-learn等で基本的な一連の流れを実装してみる」ことは非常に重要だと思っています。

ただ、慣れてきたらそれらを裏ではどのように動かしているのか、数学的な背景から理解していくことも非常に重要だと感じています。

とっつきづらい内容も多いと思いますが、少しでも理解の深化の助けとなりましたら幸いですし、私自身もここはもっとしっかり学ばなければいけないと思っていますので、学習を続けることで、より強化した記事を投稿したいと思います。