1.目的
機械学習をやってみたいと思った場合、scikit-learn等を使えば誰でも比較的手軽に実装できるようになってきています。
但し、仕事で成果を出そうとしたり、より自分のレベルを上げていくためには
「背景はよくわからないけど何かこの結果になりました」の説明では明らかに弱いことが分かると思います。
この記事では、2~3で「理論はいいからまずはscikit-learn使ってみる」こと、4以降で「その背景を数学から理解する」2つを目的としています。
※私は文系私立出身なので、数学に長けていません。可能な範囲で数学が苦手な方にもわかりやすいように説明するよう心がけました。
※線形単回帰、ロジスティック回帰Verでも同様の記事を投稿していますので、併せてお読みいただけますと幸いです。
【機械学習】線形単回帰をscikit-learnと数学の両方から理解する
[【機械学習】ロジスティック回帰をscikit-learnと数学の両方から理解する]
(https://qiita.com/Hawaii/items/ee2a0687ca451fe213be)
2.SVM(サポートベクトルマシン)とは
SVMとは、教師あり学習として、分類や回帰に用いることができるモデルです。
そして、未学習データに対して高い識別性能を得るための工夫があるため、優れた認識性能を発揮します。
出典:[Wikipedia]
(https://ja.wikipedia.org/wiki/%E3%82%B5%E3%83%9D%E3%83%BC%E3%83%88%E3%83%99%E3%82%AF%E3%82%BF%E3%83%BC%E3%83%9E%E3%82%B7%E3%83%B3)
ざっくり言うと、新しいデータを得た時に、精度の高いモデルになりやすいということです。
◆具体例
あなたはイベント企画会社の社長だとします。
昨今の猫ブームを受け、「めずらしい猫」を見に行くツアーを企画しているとします(架空の設定です)。
※「めずらしい猫」はここでは「体の大きさ」と「ヒゲの長さ」で決まるとします。
ツアー場所の候補が多すぎるため、あなたはめずらしい猫(=A)といわゆる普通の猫(=B)のデータを取りました。
そのデータを基に、今後「体の大きさ」と「ヒゲの長さ」のデータを投入すればめずらしい猫か否かを判別できるモデルを作り、めずらしい猫がいると判別された場所に注力して企画を立てることとします。
データの分布は下記のようになりました。
※青がめずらしい猫、オレンジが普通の猫です。
※X軸が体長、Y軸がヒゲの長さです。
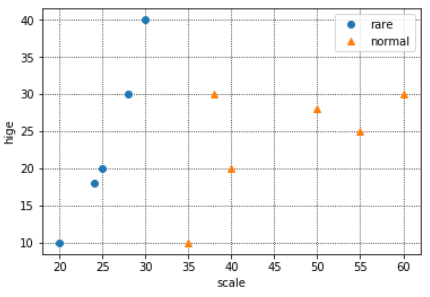
◆SVMとは
さて、上に出した分布は、青とオレンジにどのような境界線が引けそうでしょうか。
下記のように、今の手元のデータでは赤い境界も、緑の境界もありえますね。
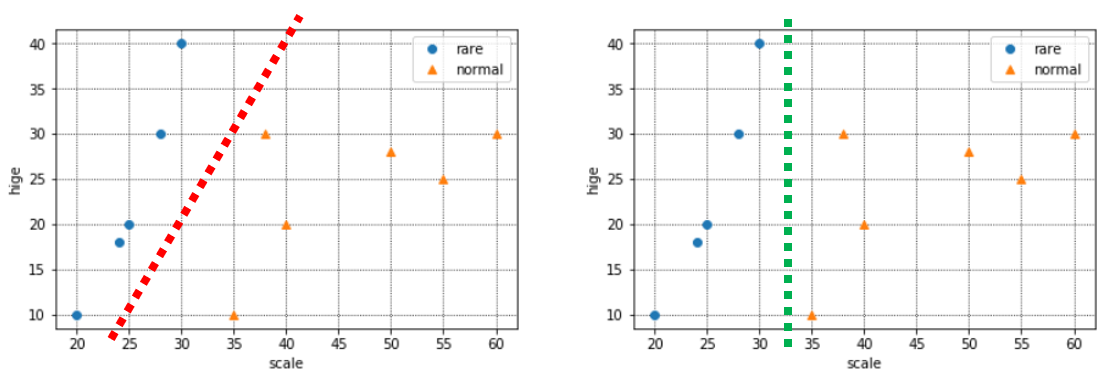
ここで、新しいデータを1つ得たので、追加でプロットしてみました。(オレンジ枠のデータです)
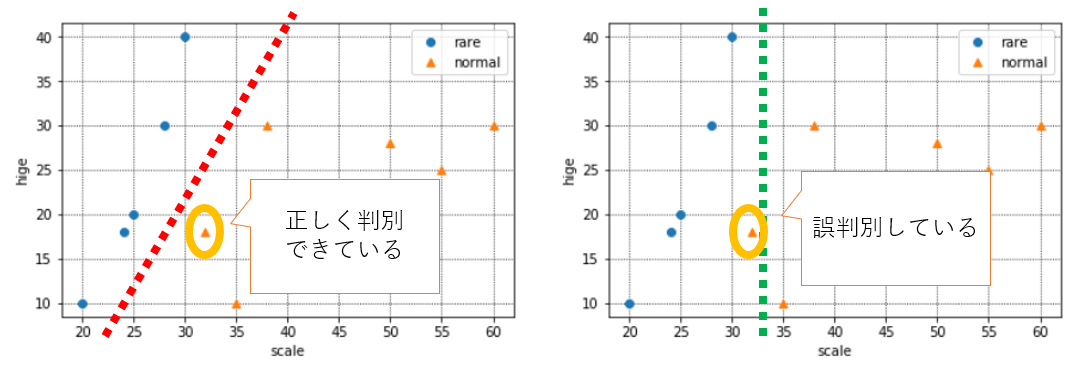
この場合、赤い境界の場合は正しく判別できていますが、緑の境界だとめずらしい猫と判別してしまっている(本来は普通の猫)ので、誤判別になります。
こういった誤判別を防ぎ正しい分類基準を見つけるため、SVMでは**「マージン最大化」という考え方を取っています。
マージンとは上の赤や緑のような境界線と、実際のデータとの距離を指します。
このマージンが大きければ、"少しだけデータが変わっただけで誤判別してしまう"ミスをなるべく小さくする**ことができるという考え方です。
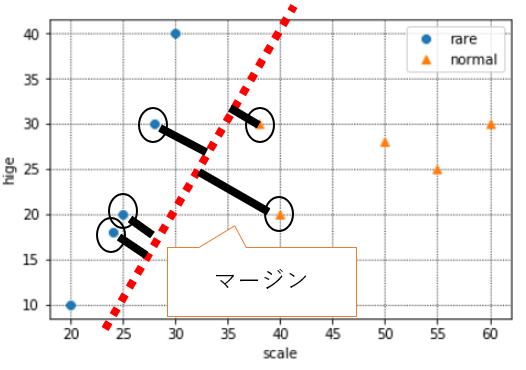
境界の近くにあるデータは、いわば「めずらしい猫」か「普通の猫」か判別に迷うデータということです。そういう、どっちか微妙なデータが多いと困るので、なるべく境界とデータの距離が遠くなるように境界を決めてあげれば、誤判別のリスクを極力抑えられますね、という考え方です。
◆ペナルティについて
とはいえ、すべてを100%完璧に分類できる境界線はなかなか存在しないものです。現実世界では、下記のように、たまには外れ値のようなデータも入ってきます。

この新たなオレンジの点まで正確に分類する境界を引こうとすると、おそらく実態にあわない境界になってしまうことは想像できると思います。(いわゆる過学習です)
実態にあった判別を行うため、SVMでは**「ある程度の誤判別」は許容しています**。
次のscikit-learnの箇所で出てきますが、じゃあ、どれくらい誤判別を許すか?は、実はモデルを構築する私たち自身が決める必要があり、それを「ペナルティ」と呼んでいます。
◆まとめると・・
SVMとは、下記2つを**「良い感じ」に実現するモデル**といえます。
・誤判別をなるべく防ぐために境界とデータの距離、つまりマージンを最大化するような境界を引こうとする
・ただし、実態にあった境界を引くため、ある程度の誤判別は許容する
3.scikit-learnでSVM
(1)必要なライブラリのインポート
SVMを行うために必要な下記をインポートしておく。
from sklearn.svm import SVC
# 下記は図示やpandas、numpyのためのライブラリ
%matplotlib inline
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
(2)データの準備
体長とヒゲのデータと、珍しい、普通の分類(めずらしい猫ががTrue,普通の猫がFalse)を下記のようにdataとして設定する。
※例えば、最初の猫は体長20センチ、ヒゲの長さが10センチで、めずらしい猫ということ。
data = pd.DataFrame({
"rare":[True,True,True,True,True,False,False,False,False,False,False,False,False],
"scale":[20, 25, 30, 24, 28, 35, 40, 38, 55, 50, 60,32,25],
"hige":[10, 20, 40, 18, 30, 10, 20, 30, 25, 28, 30,18,25],
})
(3)図示してみる(重要)
体長・ヒゲの長さとめずらしい・普通の分類を図示してみます。特徴をつかむためにも、いきなりscikit-learnを使うのではなく、どのようなデータでも図示することを心がけましょう。
y = data["rare"].values
x1, x2 = data["scale"].values, data["hige"].values
# データをプロット
plt.grid(which='major',color='black',linestyle=':')
plt.grid(which='minor',color='black',linestyle=':')
plt.plot(x1[y], x2[y], 'o', color='C0', label='rare')#青い点:yがTrue(=珍しい)のもの
plt.plot(x1[~y], x2[~y], '^', color='C1', label='normal')#オレンジの点:yがFalse(=普通)のもの
plt.xlabel("scale")
plt.ylabel("hige")
plt.legend(loc='best')
plt.show()
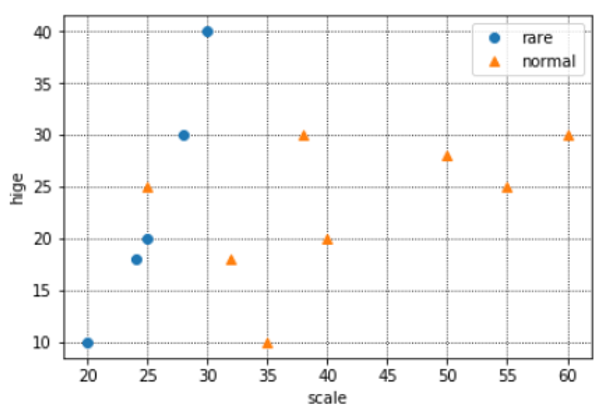
なんとなく、境界が引けそうですね。
(4)モデル構築
(ⅰ)データ整形
まずはモデル構築をするためにデータの形を整えていきます。
y = data["rare"].values#先ほどの図示と同じなので割愛してもOK
X = data[["scale", "hige"]].values
今回はpython文法の記事ではないので詳細は割愛しますが、xとyをscikit-learnでSVMするための形に整えます。
※このあたりもある程度しっかりわかっていないと書けないコードだと思うので、どこかでまとめたいと思っています。
(ⅱ)モデル構築
いよいよ、モデル構築のコードです。
C = 10
clf = SVC(C=C,kernel="linear")
clf.fit(X, y)
単純なモデルであればこれで終わりです。
clfという変数にこれからsvmモデルを作ります!と宣言のようなことを行い、次の行で、そのclfに準備したXとyをフィット(=学習)させるというイメージです。
◆引数について
SVMのモデル構築で主に考慮すべき引数は$C$とkernelです。
<$C$について>
ここではとりあえずやってみる、が主旨なので詳細は割愛しますが$C$の値を小さくすれば誤判別を許すモデルになります。
※$C$に何も指定しない、つまり「clf = SVC(kernel="linear")」と記載すると、デフォルトで$C$は1になります。
<kernelについて>
kerenelの種類は‘linear’, ‘poly’, ‘rbf’, ‘sigmoid’, ‘precomputed’があります。
[詳細は公式参照]
(https://scikit-learn.org/stable/modules/generated/sklearn.svm.SVC.html)
ここでは‘linear’と ‘rbf’を紹介します。
境界を線形(平面)に引くときはlinear、非線形に引くときはrbf(非線形カーネル関数)を用います。どちらを選ぶかで結果が変わってきます。
※ここは図示のところで違いを紹介します。
(5)構築したモデルを図示してみる
それでは、この境界を先ほどの散布図に図示してみましょう。
※このコードは少し難しいので、理解せず、コピペだけでもOKです。scikit-learnではこのような境界線を学習から算出し、この境界より右下だと文系、左上だと理系と判別しているのだと認識していただければ大丈夫です。
[参考サイト]
(https://urusulambda.wordpress.com/2018/05/19/sklearn%E3%81%A72d%E3%83%87%E3%83%BC%E3%82%BF%E3%81%AE%E3%82%B7%E3%83%B3%E3%83%97%E3%83%AB%E3%81%AAsvm%E3%82%92%E5%8F%AF%E8%A6%96%E5%8C%96%E3%81%BE%E3%81%A7/)
fig,ax = plt.subplots(figsize=(6,4))
# データの点を表示
ax.scatter(X[:,0], X[:,1], c=y)
# x座標方向に100個の値を並べる
x = np.linspace(np.min(X[:,0]), np.max(X[:,0]), 10)
# y座標方向に100個の値を並べる
y = np.linspace(np.min(X[:,1]), np.max(X[:,1]), 10)
# x,yを組み合わせた10000個の点のx座標と,y座標の配列
x_g, y_g = np.meshgrid(x, y)
# np,c_で二つの座標を結びつけ, SVMに渡す
z_g = clf.predict(np.c_[x_g.ravel(), y_g.ravel()])
# z_gは配列の列になっているが、グラフに表示するために(100, 100)の形に戻す
z_g = z_g.reshape(x_g.shape)
# 境界線の色塗り
ax.contourf(x_g,y_g,z_g,cmap=plt.cm.coolwarm, alpha=0.8);
# 最後に表示
plt.show()
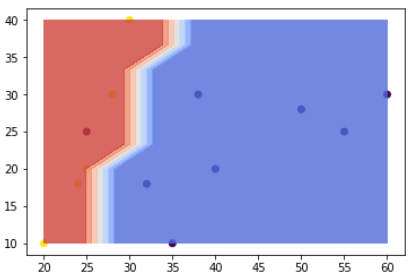
モデル構築の結果、上記のように境界が引けました。
これ以降新しいデータが入ってきた場合、青い領域にプロットされれば普通の猫、赤い領域にプロットされれば珍しい猫と分類されるわけです。
ちなみに、(4)の◆引数について で紹介したkernelをrbfにすると、下記のような境界になります。
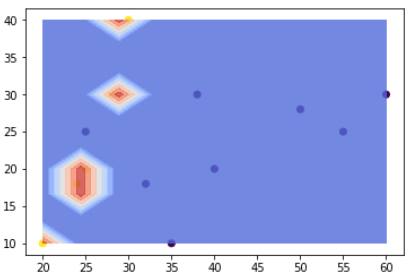
全く違う境界になっていますね!今回のケースで言うと、線形の方が適切にデータの境界を引けている気がするので、kernelはlinearを使うことにしましょう。
(6)現実世界では・・
モデルを作って終わり、では意味ないですね。現実世界では、この予測モデルを使って、新たな猫のデータを取得した際、めずらしいか普通かの区別をすることが大切です。
あなたは別の2種類分の情報を得て、データをメモしました。
それを下記のようにzという変数に格納します。
z = pd.DataFrame({
"scale":[28, 45],
"hige":[25, 20],
})
z2 = z[["scale", "hige"]].values
このデータと、境界がlinearの方の図示を見比べると、おそらく1匹目が赤(めずらしい=True)、2匹目が青(普通=False)に分類される気がしますね。
では、予測をしてみましょう。
y_est = clf.predict(z2)
このようにすると、y_estには([ True, False])と結果が表示されたので、境界線通りに分類されていることが分かります。
4.SVMを数学から理解する
さて、3まではscikit-learnを用いてSVMモデルを構築→図示→別の2匹の猫のめずらしい・普通を予測するという流れを実装してみました。
ここでは、この流れのSVMモデルは、数学的にはどのように計算されているのかを明らかにしていきたいと思います。
※現状はこの知識は必要ないという方は読み飛ばしていただいて結構です。
(1)マージン最大化について
「2.SVM(サポートベクトルマシン)とは」で記載した、マージン最大化について掘り下げていこうと思います。
各データの点と境界までの距離が最も大きくなる部分が最適な境界線と説明しましたが、それはつまりどういう状態を指すのでしょうか。

◆立体的な可視化
今まで図示していた散布図を、少し立体的に書き換えてみると、下記のようになります。
※オレンジの点(normal)部分を浮き上がらせて、横から見たイメージと捉えてください。

上の赤い境界線を通る緑の平面が境界と考えると、この平面の**「傾き」**を変えることで、マージン(=データと境界線までの距離)が変わることがイメージとしてつくでしょうか。
例えば、この平面の傾きを急にすると、下記のようにマージンは小さくなります。

逆に、平面の傾きを緩やかにすると、下記のようにマージンは大きくなります。

つまり、「データをきれいに分類することができる」かつ、「なるべく決定境界を通る平面の傾きが緩やかになる」ことが、最適な境界の条件ということです。
◆マージンの式
それでは、**「なるべく決定境界を通る平面の傾きが緩やかになる」**とはどういうことでしょうか。さらに図示していきます。

境界面を横から見た図を表してみました。この式は$w_1x_1+w_2x_2$と表されます。
先ほど記載したとおり、マージンが最大とは、「なるべく決定境界を通る平面の傾き(=勾配)が緩やかになる」ことでした。
最も傾き(=勾配)が緩やかということは、$x_1$や$x_2$を多少動かしても$w_1x_1+w_2x_2$に与える影響が小さいということ(=傾きが緩やかなので、多少$x$の値を動かしても式全体の値はたいして変わらないですよね)、つまり「$w_1,w_2$の値が小さいということ」です。
これを数式にすると下記になりますが、この数式の意味を理解するにはノルムの理解が必要で複雑になるため、この時点では「境界線の式の$w_1$と$w_2$がなるべく小さくなるように計算されているのだ」、と理解しておけばOKです。
$||w||_2^2$ ←これが最小になれば、マージンが最大化される
(2)ペナルティについて
基本的な考え方は(1)で終わりですが、「2.SVM(サポートベクトルマシン)とは」の「◆ペナルティについて」で述べたように、実態に即した分類ができるように、ある程度の誤判別を許容します。
この、どの程度誤判別を許すか?の程度をペナルティと呼んでいます。
ペナルティの式は下記のように表され、$ξ$はヒンジ損失関数と呼ばれます。
$C(\sum_{i=1}^n ξi)$
$C$は(ⅱ)モデル構築で記載した引数と同じ意味ですが、この$C$を大きくするほど誤判別を許さない式になります(=大きくしすぎると過学習しやすくなります)。
この式について深く理解しようとするとかなり突っ込んだ理解が必要になるため、今回はこのあたりまでにしておこうと思います。
(後々、別建てにするかもしれないですがここもまとめていきたいです)
(3)まとめると・・
(1)(2)から、SVMは下記の目的関数を、なるべく小さくするように計算されています。
直感的には、「マージン最大化のために」境界面の傾きがなるべく小さくなるようにしていますが、実態に即した分類をするために、誤判別をどれくらい許すか?のペナルティ項を加え、全体のバランスが良い感じになるように境界面の式が設定されています。
||w||_2^2 +
C(\sum_{i=1}^n ξi)
5.まとめ
いかがでしたでしょうか。
SVMは単回帰やロジスティック回帰よりも背景の数学的理解が必要なため、そこまで深くは記載できていませんが、ここまでの理解だけでも、以前より理解の深化の助けになりましたら幸いです。

