最近数学をやり直していてふと機械学習がどういう仕組みなのか知りたくなって、Courseraでスタンフォード大学が提供している機械学習講座を受けている。第6週まで終わったので思い出しながら軽くまとめる。講座はこちら Coursera Machine Learning
week1 機械学習とは何か、単線形回帰、仮説関数、コスト関数、最急降下法
week2 重線形回帰、スケーリング、多項式回帰、正規方程式
week3 ロジスティック回帰、共役勾配法・BFGS・L-BFGS、多クラス分類 、過学習と正則化
week4 ニューラルネットワークの基礎
week5 ニューラルネットワークのコスト関数とバックプロパゲーション
week6 機械学習のモデルの評価 - 交差検証、バイアスとバリアンス、学習曲線、適合率と再現率
Week 1 機械学習とは何か、単線形回帰、仮説関数、コスト関数、最急降下法
機械学習とは何か
定義
古くからある非公式な定義
Arthur Samuel: 明示的にプログラムしていなくてもコンピュータに学習する能力を与える学問。
現代的な定義
Tom Mitchell: タスクTのパフォーマンスが確率Pで計測され、経験Eで向上する場合に、コンピュータプログラムは、あるクラスのタスクTとパフォーマンス指標Pに関して、経験Eから学ぶと言われている。(例えば、E = あるゲームをプレイする経験、T = あるゲームをプレイするタスク、P = あるゲームに次勝つ確率)
機械学習は、一般に__教師あり学習__と__教師なし学習__に分けられる。
教師あり学習
__教師あり学習__は、あるデータがあったときにそのデータが入力と出力の関係にあり、入力に対して正しい出力がなんであるかあらかじめ知っている場合の学習である。
また教師あり学習は、__回帰問題__と__分類問題__に分けられる。
回帰問題
__回帰問題__は、入力に対する出力が連続値を取るような結果になるものに対して予測しようとする問題。例えば、不動産の大きさに対して価格がどう予測されるかというような問題である。
分類問題
__分類問題__は、その名の通りデータをどう分類すべきかという問題。例えば、患者の腫瘍が良性であるか悪性であるかどちらに分類すべきかというような問題である。
教師なし学習
__教師なし学習__は、結果がわからないデータに対して、データの構造を導き出してグループ化する学習。例えば、遺伝子情報を寿命や場所、役割などの変数によって類似または関連するグループに自動的にグループ化するような学習である。
単線形回帰 - Linear Regression with One Variable
仮説関数 - Hypothesis Function
$x^{(i)}$は入力の変数を、$y^{(i)}$は出力を表す。これらがペアになった$\{x^{(i)},y^{(i)}\}$をトレーニングセットと呼ぶ。例えば不動産の大きさ$x^{(i)}$に対して、価格$y^{(i)}$のトレーニングセットを思い浮かべると理解しやすい。
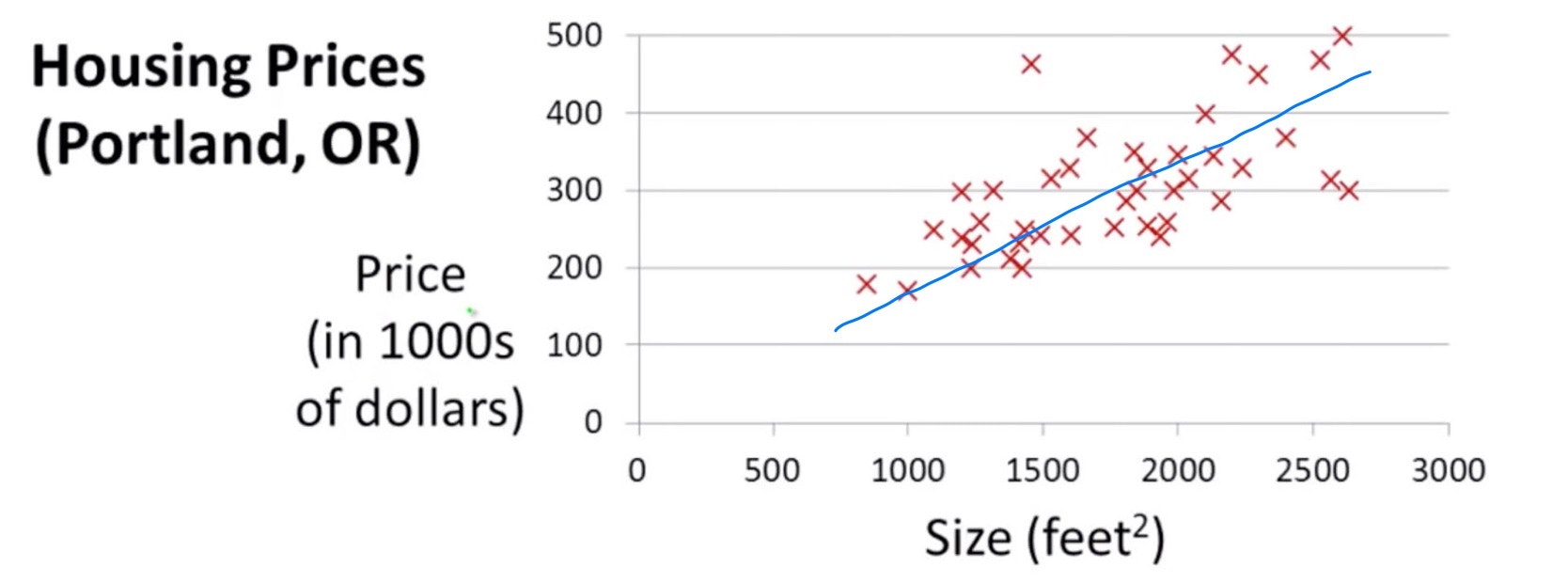
このようなトレーニングセットに対して、一本の直線が引けることがわかる。この直線つまり一次関数を学習することが単線形回帰の目的である。この一次関数のことを仮説関数という。以下のように表すことができる。
y = h\theta(x)=\theta_0+\theta_1x
以下の図は、トレーニングセットを学習して、xとyの関係を表す関数$h\theta(x)$を求めるというプロセスを表している。
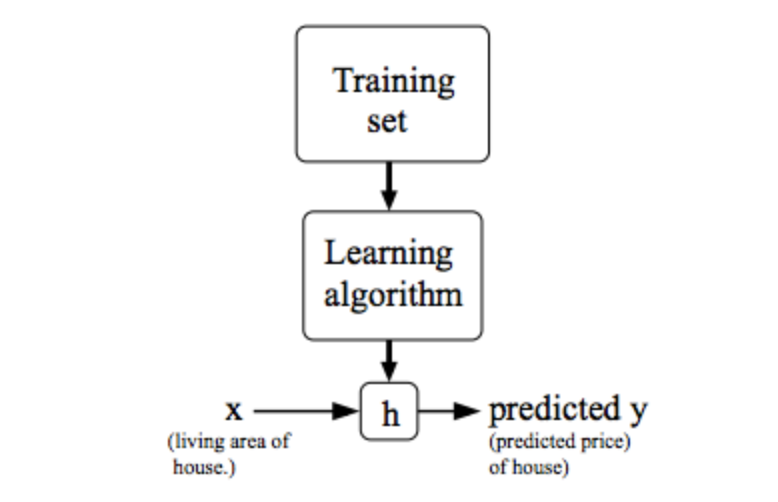
コスト関数 - Cost Function
仮説関数がトレーニングセットに近似すればするほど、良い予測モデルが手に入るということになる。したがって仮説関数をデータにフィットするようなパラメータ$\theta$を求める必要がある。
h\theta(x)=\theta_0+\theta_1x
コスト関数を使うことによって、仮説関数がどれくらいデータにフィットしているかの精度を測ることができる。コスト関数は、仮説関数で計算された予測結果と実際のデータの値$y$の差を二乗して、その総和をデータの総数で割ることで計算される。つまり最小二乗法を使っている。
$\frac{1}{2m}$と2で割っているのはあとで行う微分の計算を楽にするためである。コスト関数は下に凸二次関数となるため、適当な係数を掛けても最小値は変わらないので問題ない。
J(\theta_0,\theta_1)=\frac{1}{2m}\sum_{i=1}^{m}(h\theta(x_i)−y_i)^2
最急降下法 - Gradient Descent
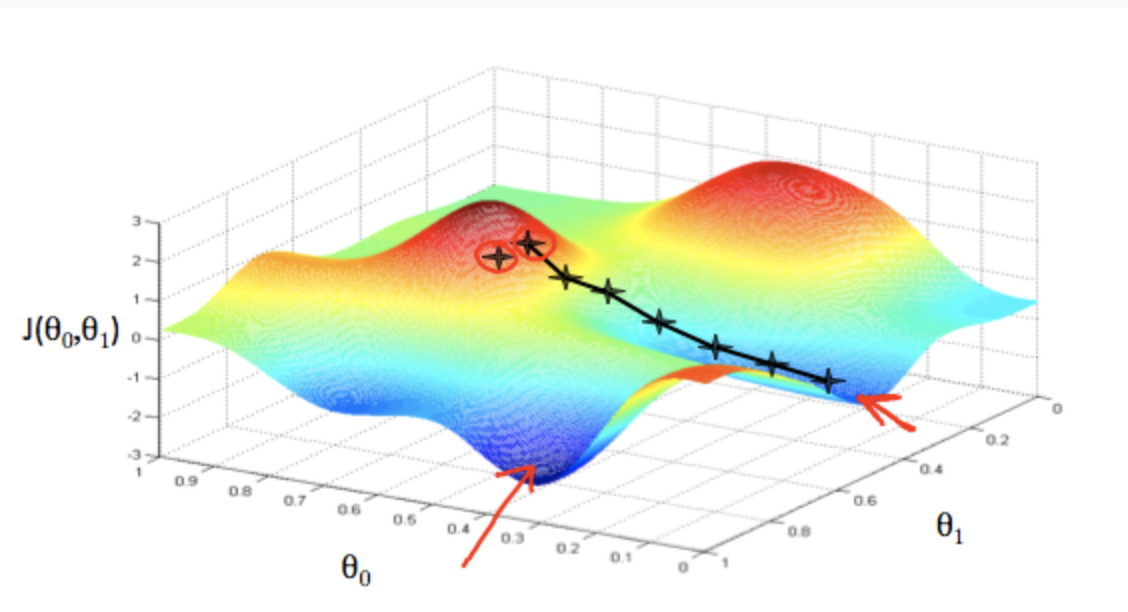
コスト関数の最小値が、仮説関数と実際の値の誤差の最も少ない場所なので、これを求めたい。最小値を求めるアルゴリズムの一つに最急降下法がある。以下のようにコスト関数$J(\theta_0,\theta_1)$を$\theta_j$について偏微分して$\theta_j$との差をとったものを自分自身に代入して更新していく。
\theta_j:=\theta_j−α\frac{∂}{∂\theta_j}J(\theta_0,\theta_1)
コスト関数を代入して計算すると以下のようになる。
\theta_j:= \theta_j−α\frac{1}{m}\sum_{i=1}^{m}((h\theta(x_i)−y_i)x_i)
何度もパラメータの更新を繰り返し、最終的には値が収束して傾きが十分小さくなる。するとそこが最小値となる。ここで本来の目的である仮説関数のパラメータ$\theta$を求めることができた。トレーニングセットに対して、最もフィットする直線が引けたということである。
ちなみにαは学習率と言ってパラメータ更新の変動率に影響を及ぼす係数である。これは大きすぎず小さすぎずちょうど良い値を選ぶ必要がある。
以下の図は最急降下法でパラメータの更新を繰り返し、$J(\theta_0,\theta_1)$の最小値を求めていく様子。