最近数学をやり直していてふと機械学習がどういう仕組みなのか知りたくなって、Courseraでスタンフォード大学が提供している機械学習講座を受けている。第6週まで終わったので思い出しながら軽くまとめる。講座はこちら Coursera Machine Learning
week1 機械学習とは何か、単線形回帰、仮説関数、コスト関数、最急降下法
week2 重線形回帰、スケーリング、多項式回帰、正規方程式
week3 ロジスティック回帰、共役勾配法・BFGS・L-BFGS、多クラス分類 、過学習と正則化
week4 ニューラルネットワークの基礎
week5 ニューラルネットワークのコスト関数とバックプロパゲーション
week6 機械学習のモデルの評価 - 交差検証、バイアスとバリアンス、学習曲線、適合率と再現率
Week 6 機械学習のモデルの評価 - 交差検証、バイアスとバリアンス、学習曲線、適合率と再現率
交差検証 - Cross Validation
あるデータセットに学習アルゴリズムがよく適合しているからと言って、それがいいモデルであるとは言えない。なぜならそのモデルに新しいデータセットを与えた時、同じようによく適合するとは言えないからである。
この問題を改善するために、以下のように3つにデータセットを分ける。
- トレーニングセット 60%
- 交差検証セット 20%
- テストセット 20%
そして、以下のようなステップで誤差を計算していく。
- トレーニングセットを使って、$\Theta$を最適化する。
- 交差検証セットを使って、誤差が最も小さい多項式の次数$d$を探す。
- テストセットを使って、$J_{test}(\Theta^{(d)})$の誤差を見積もる。
バイアスとバリアンス - Bias and Variance
多項式の次数

| 左 | 中央 | 右 |
|---|---|---|
| 高バイアス - High Bias | 高バリアンス - High Variance | |
| 未学習 - Underfit | Justfit | 過学習 - Overfit |
| $y=\theta_0+\theta_1x$ | $y=\theta_0+\theta_1x+\theta_2x^2$ | $y=\sum_{j=0}^5\theta_jx^j$ |
上の図から分かるように、次数が大きくなるほどトレーニングセットの誤差は小さくなる。
同時に、交差検証の誤差は、ある点までは次数が大きくなるにつれて減少し、さらに次数が大きくなると増加する。つまり、以下のように次数$d$と$J(\Theta)$の関係をグラフにした場合、下に凸曲線を形成する。
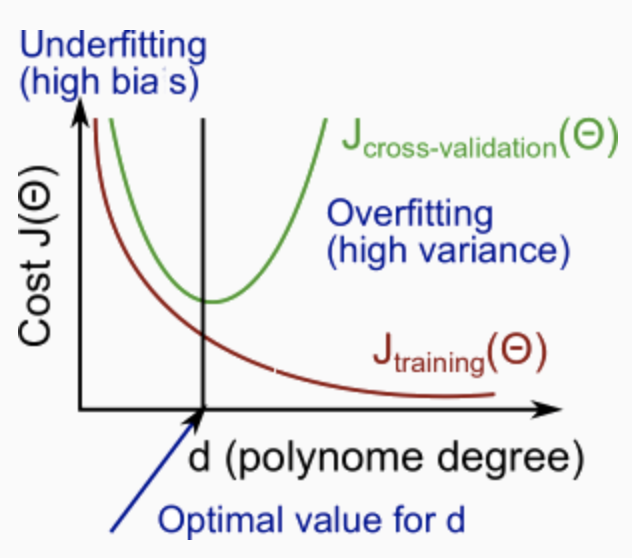
正則化項λ
次に正則化項$\lambda$との関係について考える。
$\lambda$は大きくなればなるほどunderfitし、小さくなればなるほどoverfitする。
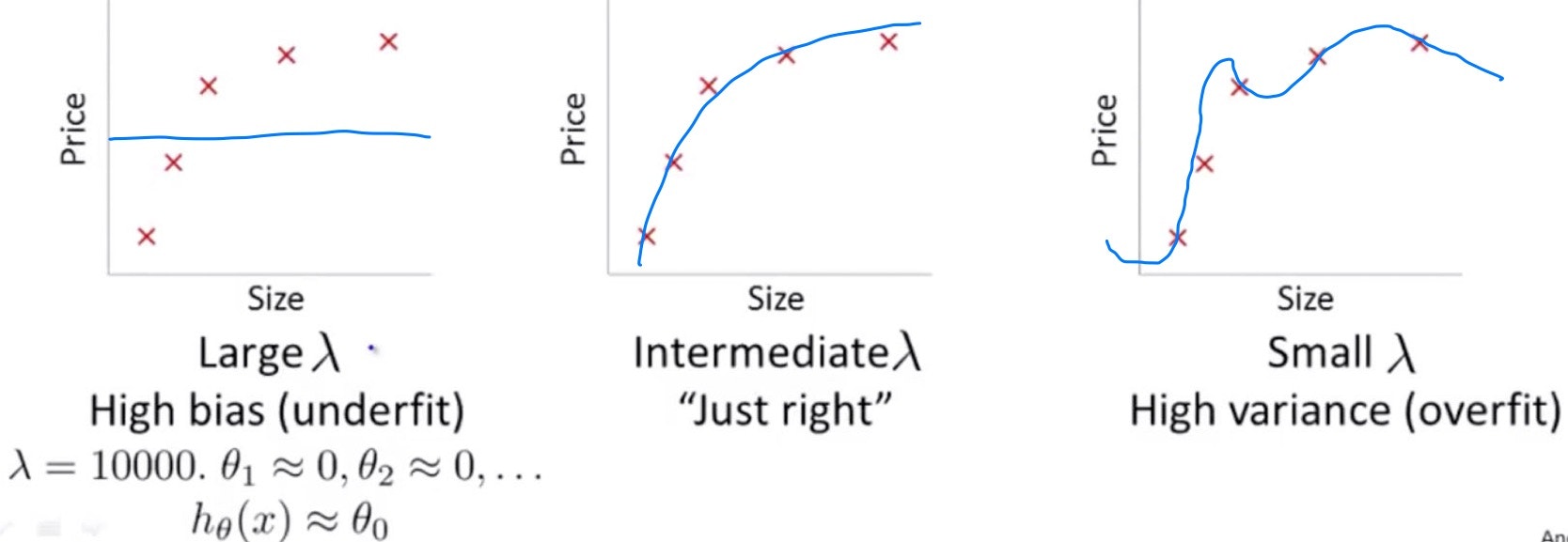
$\lambda$と$J(\Theta)$の関係をグラフにすると以下のようになる。
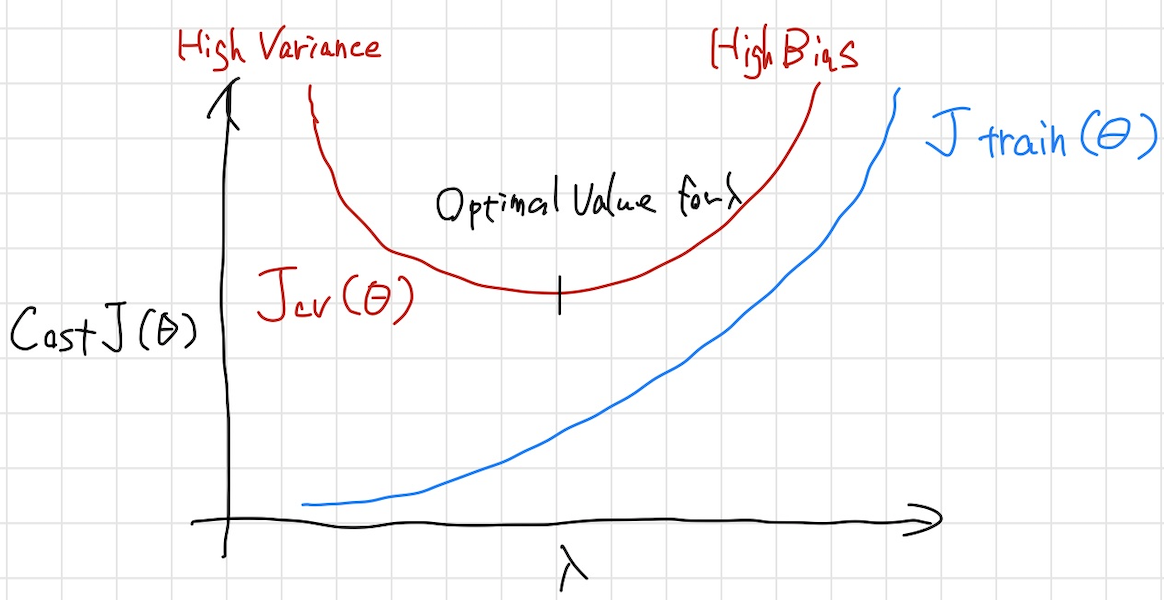
学習曲線 - Learning Curves
ごく少数のデータセットでアルゴリズムをトレーニングすると誤差が0になりやすくなる。なぜなら、例えばデータセットが2つや3つの場合、そのデータセットには二次関数がぴったりフィットするから。一般に、トレーニングセットが大きくなるほど誤差が大きくなる。そして一定まで達すると安定する。
高バイアスの場合、
- トレーニングセットが小さい時: $J_{train}(\Theta)$は低く、$J_{cv}(\Theta)$は高くなる
- トレーニングセットが大きい時: $J_{train}(\Theta)$と$J_{cv}(\Theta)$の両方が高くなり、同じような値になる
グラフにすると以下のようになる。

つまり、高バイアスの場合トレーニングセットを増やすのはあまり効果的ではない。
高バリアンスの場合、
- トレーニングセットが小さい時: $J_{train}(\Theta)$は低く、$J_{cv}(\Theta)$は高くなる
- トレーニングセットが大きい時: $J_{train}(\Theta)$は大きくなり、$J_{cv}(\Theta)$は小さくなり続ける
グラフにすると以下のようになる。

つまり、高バリアンスの場合トレーニングセットを増やすことは効果的である。
適合率と再現率- Precision and Recall
歪んだクラス - Skewed Classes
例えば、腫瘍を良性か悪性か分類する時、実際には悪性である患者が100人中2人いる場合に全ての人を良性に分類する予測を立てたとする。その予測は結果として98%の的中率を持つことになる。さて、これはいい予測と言えるだろうか。
適合率と再現率
予測の精度を図るために用いられる指標が適合率と再現率である。
予測した結果と実際の値を以下のような表にする。
| 予測されたクラス \ 実際のクラス | 1 | 0 |
|---|---|---|
| 1 | True Positive(TP) | False Positive(FP) |
| 0 | False Negative(TN) | True Nagative(TN) |
適合率と再現率は以下のように表される。
$Precision(適合率)=\frac{TP}{TP+FP}$
$Recall(再現率)=\frac{TP}{TP+FN}$
0-1の値をとり、高くなるほど精度が高いと言える。
上にあげた全ての腫瘍を良性と予測する場合は再現率が0になる。
F値 - F Score
適合率と再現率はトレードオフの関係にある。どちらもいい具合に高くないと良いアルゴリズムとは言えない。それを判断するためにF値を使用する。
$F=2\frac{PR}{P+R}$