最近数学をやり直していてふと機械学習がどういう仕組みなのか知りたくなって、Courseraでスタンフォード大学が提供している機械学習講座を受けている。第6週まで終わったので思い出しながら軽くまとめる。講座はこちら Coursera Machine Learning
week1 機械学習とは何か、単線形回帰、仮説関数、コスト関数、最急降下法
week2 重線形回帰、スケーリング、多項式回帰、正規方程式
week3 ロジスティック回帰、共役勾配法・BFGS・L-BFGS、多クラス分類 、過学習と正則化
week4 ニューラルネットワークの基礎
week5 ニューラルネットワークのコスト関数とバックプロパゲーション
week6 機械学習のモデルの評価 - 交差検証、バイアスとバリアンス、学習曲線、適合率と再現率
Week 3 ロジスティック回帰、共役勾配法・BFGS・L-BFGS、多クラス分類 、過学習と正則化
ロジスティック回帰
今回は分類問題を扱う。例えば、患者の腫瘍が良性か悪性か分類するというような問題。
シグモイド関数
仮説関数には、以下のようなシグモイド間数と呼ばれるものを使用する。
h\theta(x)=g(\theta^Tx)\\
z=\theta^Tx\\
g(z)=\frac{1}{1+e^{−z}}

この関数は入力に対して、0から1の出力をとる。$0$と$1$に分類する場合に入力に対して出力が$0.8$を取れば$1$に分類される確率が$80$%であるというように表すことができる。
決定境界
シグモイド関数のちょうど真ん中$0.5$をしきい値として$0$と$1$を分類する線を引く。これを決定境界という。つまり以下のように表すことができる。
$$
h\theta(x)≥0.5\hspace{2pt}\rightarrow\hspace{2pt}y=1\
h\theta(x)<0.5\hspace{2pt}\rightarrow\hspace{2pt}y=0
$$
\theta^Tx≥0\hspace{2pt}\rightarrow\hspace{2pt}y=1\\
\theta^Tx<0\hspace{2pt}\rightarrow\hspace{2pt}y=0
決定境界もまた線形だけでなく非線形を表すことができる。$z=\theta_0+\theta_1x_1^2+\theta_2x^2$のように。
コスト関数
コスト関数は以下のように表される。
\begin{align}
J(\theta)&=\frac{1}{m}\sum_{i=1}^mCost(h\theta(x^{(i)}),y^{(i)})\\
Cost(h\theta(x),y)&=−\log(h\theta(x))\quad if\hspace{4pt}y=1\\
Cost(h\theta(x),y)&=−\log(1−h\theta(x))\quad if\hspace{4pt}y=0
\end{align}
$y$が$0$の場合、仮説関数が0だとコスト関数は$0$になる。仮説関数が$1$に近づくと、コスト関数は無限大に近づく。
$y$が$1$の場合、仮説関数が1だとコスト関数は$0$になる。仮説関数が$0$に近づくと、コスト関数は無限大に近づく。
上記は一つの式にまとめることができる。つまりこのコスト関数は尤度関数の$\log$を取ったものだということ。
J(\theta)=−\frac{1}{m}\sum_{i=1}^{m}[y^{(i)}\log(h_\theta(x^{(i)}))+(1−y^{
(i)})\log(1−h_\theta(x^{(i)}))]
最急降下法
パラメータ更新式はいつも通り以下のようになる。
\theta_j:=\theta_j−α\frac{∂}{∂\theta_j}J(\theta)
コスト関数を代入して偏微分を計算すると
\theta_j:=\theta_j−\frac{α}{m}\sum_{i=1}^{m}(h\theta(x^{(i)})−y^{(i)})x^{(i)}_j
共役勾配法・BFGS・L-BFGS - Conjugate Gradient・BFGS・L-BFGS
最急降下法より速くて学習率を設定する必要のないアルゴリズムの紹介。詳しい仕組みは複雑なので割愛。
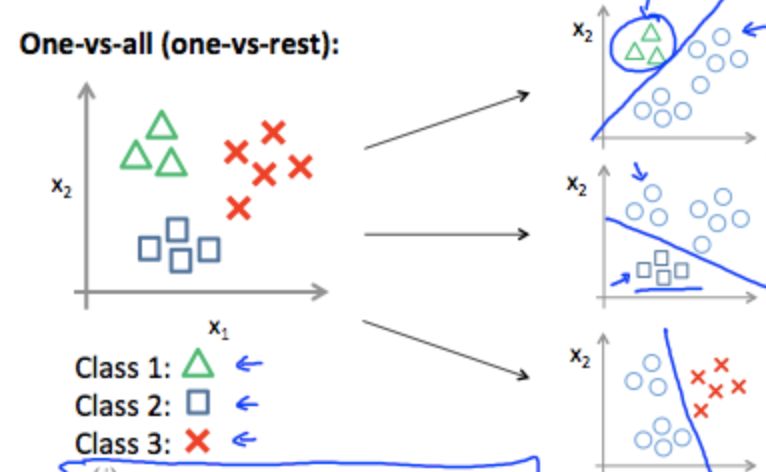
多クラス分類 - Multiclass Classification: One-vs-all
今まで見てきたのは、$y=\{0,1\}$で表されるような二値分類だったが、今回は$y=\{0,1...n\}$で表されるような多クラス分類を考える。
まず一つのクラスを選び、残った全てのクラスをもう一つにまとめて二つのクラスを作る。そしてそれぞれのケースにロジスティック回帰を適用して最も高い値を返した仮説を使用する。
y\in\{0,1...n\}\\
h^{(0)}_\theta(x)=P(y=0|x;\theta)\\
h^{(1)}_\theta(x)=P(y=1|x;\theta)\\
⋯\\
h^{(n)}_\theta(x)=P(y=n|x;θ)\\
prediction=max_i(h^{(i)}_\theta(x))
過学習と正則化 - Overfitting and Regularization
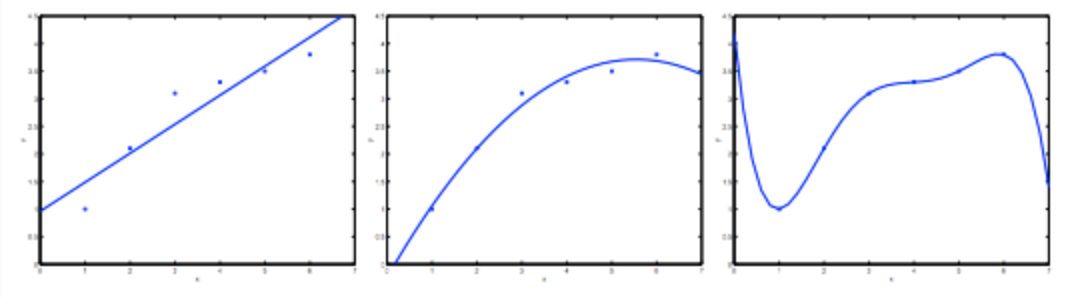
過学習
左は$y=\theta_0+\theta_1$x
中央は$y=\theta_0+\theta_1x+\theta_2x^2$
右は$y=\sum_{j=0}^5\theta_jx^j$
左は未学習の例で右は過学習の例。高バイアス、高バリアンスともいう。
未学習はデータと仮説が近似してないので直感的によくないと理解できるが、過学習もよくない。なぜなら既知のトレーニングデータにはぴったりと合うが、肝心の予測するための新しいデータには合わない可能性が高いから。
では、過学習に対処するためにはどうするか。以下の二つの方法がある。
1.特徴量を減らす
2.正則化
正則化
コスト関数
例えば、以下のような仮説関数がある。
\theta_0+\theta_1x+\theta_2x_2+\theta_3x_3+\theta_4x_4
この時、$\theta_3x_3+\theta_4x_4$の影響を排除したい。
$\theta_3$と$\theta_4$を0に近づけるためにコスト関数を以下のようにする。これで大幅に$\theta_3$と$\theta_4$の値が減少する。それは過学習を抑制する意味を持つ。
min_\theta\frac{1}{2m}\sum_{i=1}^m(h_\theta(x^{(i)})−y^{(i)})^2+1000⋅\theta_3^2+1000⋅\theta_4^2
これを一般化して以下のようにする。$\lambda$は正則化の項。
min_\theta\frac{1}{2m}\sum_{i=1}^m(h_\theta(x^{(i)})-y^{(i)})^2+\lambda\sum_{j=1}^{n}\theta_j^2
正則化は線形回帰とロジスティック回帰どちらにも適用することができる。
最急降下法を使って以下のようにパラメータを更新する。
\begin{align}
\theta_0&:=\theta_0−\alpha\frac{1}{m}\sum_{i=1}^{m}(h_\theta(x^{(i)})−y^{(i)})x^{(i)}_0\\
\theta_j&:=\theta_j−\alpha\Bigl[\Bigl(\frac{1}{m}\sum_{i=1}^{m}(h_\theta(x^{(i)})−y^{(i)})x^{(i)}_j\Bigr)+\frac{\lambda}{m}\theta_j\Bigr]\hspace{12pt}j\ni\{1,2...n\}
\end{align}