最近数学をやり直していてふと機械学習がどういう仕組みなのか知りたくなって、Courseraでスタンフォード大学が提供している機械学習講座を受けている。第6週まで終わったので思い出しながら軽くまとめる。講座はこちら Coursera Machine Learning
week1 機械学習とは何か、単線形回帰、仮説関数、コスト関数、最急降下法
week2 重線形回帰、スケーリング、多項式回帰、正規方程式
week3 ロジスティック回帰、共役勾配法・BFGS・L-BFGS、多クラス分類 、過学習と正則化
week4 ニューラルネットワークの基礎
week5 ニューラルネットワークのコスト関数とバックプロパゲーション
week6 機械学習のモデルの評価 - 交差検証、バイアスとバリアンス、学習曲線、適合率と再現率
Week 2 重線形回帰、スケーリング、多項式回帰、正規方程式
重線形回帰
前回の単線形回帰では単一の変数しか扱わなかったが、今回の重線形回帰では多変数を扱う。前回とは異なり入力の変数$x$をいくつでも持つことができる。
仮説関数 - Hypothesis Function
仮説関数は以下のように表される。
h\theta(x)=\theta_0+\theta_1x_1+\theta_2x_2+\theta_3x_3+⋯+\theta_nx_n = \theta^Tx
パラメータの更新式は前回と同じく以下のようになる。異なるのは同時に更新すべきパラメータ$\theta$が増えること。
\theta_j:=\theta_j−α\frac{1}{m}\sum_{i=1}^{m}(h\theta(x^{(i)})−y^{(i)})⋅x^{(i)}_{j}
特徴量スケーリング - Feature Scaling
効率的に最急降下法を走らせるためにスケーリングという手段を使って、変数を$−1≤x_{(i)}≤1$のように一定の範囲に収まるようにする。スケーリングには正規化と標準化という方法がある。
正規化 - Normalization
正規化は以下のように表される。特徴量$x_i$から特徴量の最小値を引いたものを、特徴量の最大値から最小値を引いたもので割る。
x_i:=\frac{x_i-x_{min}}{x_{max}-x_{min}}
標準化 - Standardization
標準化は以下のように表される。特徴量$x_i$から平均$μ_i$を引いたものを$x$の標準偏差で割る。
x_i:=\frac{x_i-μ_i}{s_i}
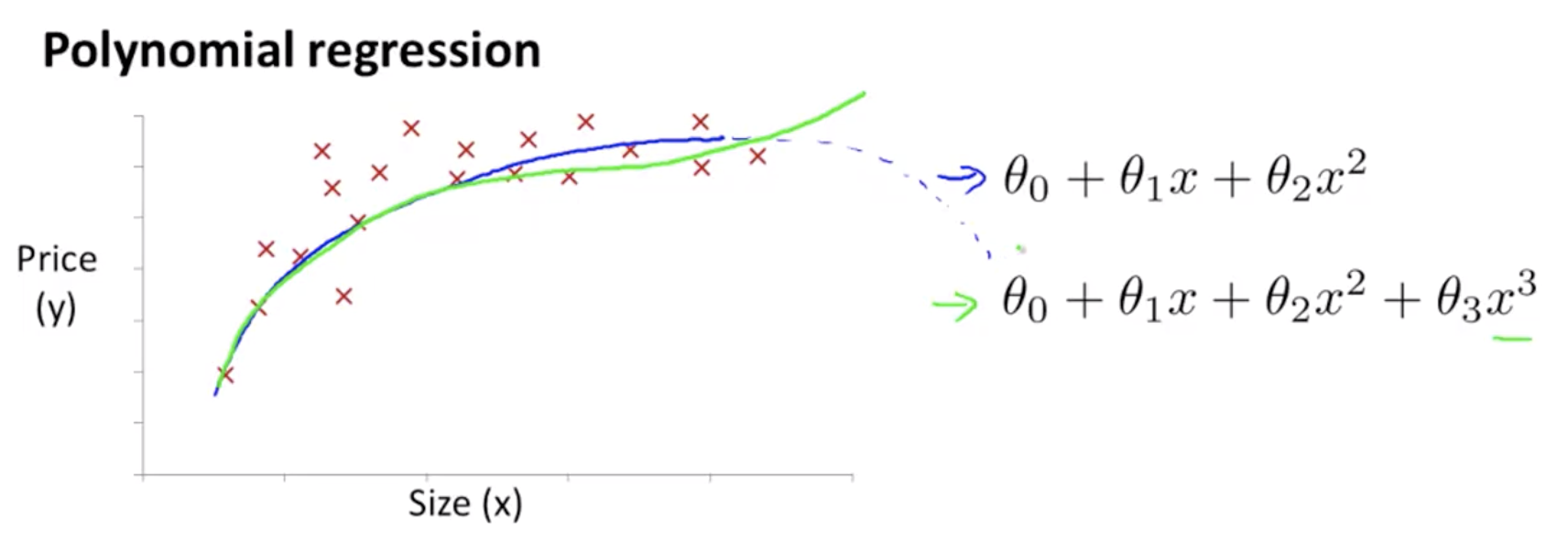
多項式回帰
仮説関数に多項式を用いることで、線形ではなく非線形を表すことが可能となる。
$$
h\theta(x)=\theta_0+\theta_1x_1+\theta_2x_1^2+\theta_3x_1^3
$$
正規方程式
コスト関数の最小値を求めるために最急降下法を使ったが、もう一つの方法が正規方程式を使った方法。コスト関数の傾きが$0$になる時のパラメータが知りたいので、コスト関数を微分したものを$=0$として解けばよい。正規方程式は方程式なので、最急降下法と異なり反復する必要がない。以下のように表すことができる。
$$\theta=(X^TX)^{−1}X^Ty$$
最急降下法と正規方程式にはそれぞれメリットデメリットがある。
| 最急降下法 | 正規方程式 | |
|---|---|---|
| 学習率 | 設定する必要あり | 設定する必要なし |
| 反復 | 必要あり | 必要なし |
| 計算量 | $O(kn^2)$ | $O(n^3)$ |
| 特徴量 | 多くてもよく動く | 多いと遅い |