最近数学をやり直していてふと機械学習がどういう仕組みなのか知りたくなって、Courseraでスタンフォード大学が提供している機械学習講座を受けている。第6週まで終わったので思い出しながら軽くまとめる。講座はこちら Coursera Machine Learning
week1 機械学習とは何か、単線形回帰、仮説関数、コスト関数、最急降下法
week2 重線形回帰、スケーリング、多項式回帰、正規方程式
week3 ロジスティック回帰、共役勾配法・BFGS・L-BFGS、多クラス分類 、過学習と正則化
week4 ニューラルネットワークの基礎
week5 ニューラルネットワークのコスト関数とバックプロパゲーション
week6 機械学習のモデルの評価 - 交差検証、バイアスとバリアンス、学習曲線、適合率と再現率
Week 4 ニューラルネットワークの基礎
ニューラルネットワーク - Neural Networks
必要性
ニューラルネットワークは古くからあるアルゴリズムで、人間の脳の仕組みをシュミレートしたものである。
ニューラルネットワークがなぜ必要なのか。今までは不動産の大きさや場所をもとに価格を予測するというような特徴量が少なく、単純で線形に近い仮説の問題を前提として考えていた。今回は複雑で非線形な仮説の問題を思い浮かべてみる。例えば、画像から車を検出する問題。画像はいくつものピクセルからなるため特徴量の数が膨大になる。その場合、単純なロジスティック回帰を使おうとすると計算コストが膨大になり、仮説をフィットさせることが難しくなり向いていない。ニューラルネットワークは、このような複雑で非線形な仮説を学習させることに向いている。
仮説関数
ニューラルネットワークでは、分類問題と同じようにロジスティック関数を使用する。これは活性化関数とも呼ばれる。
視覚的には以下のように表される。

左から1番目のレイヤーを入力層といい、そこから入力されたものが2番目のノードに入り、最後に出力層と呼ばれる仮説関数に出力される。
以下のようにレイヤーを増やすことができる。
 増やした左から2番目のレイヤーは隠れ層といい、$a_0^{(2)}⋯a_n^{(2)}$は活性化ユニットと呼ばれる。
増やした左から2番目のレイヤーは隠れ層といい、$a_0^{(2)}⋯a_n^{(2)}$は活性化ユニットと呼ばれる。
以下のように、活性化ノードを計算して最終的な出力を得る。
\begin{align}
a^{(2)}_1&=g(\Theta^{(1)}_{10}x_0+\Theta^{(1)}_{11}x_1+\Theta^{(1)}_{12}x_2+\Theta^{(1)}_{13}x_3)\\
a^{(2)}_2&=g(\Theta^{(1)}_{20}x_0+\Theta^{(1)}_{21}x_1+\Theta^{(1)}_{22}x_2+\Theta^{(1)}_{23}x_3)\\
a^{(2)}_3&=g(\Theta^{(1)}_{30}x_0+\Theta^{(1)}_{31}x_1+\Theta^{(1)}_{32}x_2+\Theta^{(1)}_{33}x_3)\\
h\Theta(x)=a^{(3)}_1&=g(\Theta^{(2)}_{10}a^{(2)}_0+\Theta^{(2)}_{11}a^{(2)}_1+\Theta^{(2)}_{12}a^{(2)}_2+\Theta^{(2)}_{13}a^{(2)}_3)
\end{align}
最終的に仮説関数として出力されるものは、各活性化ユニットの和にロジスティック関数を適用したものである。
またこの時、重み行列$\Theta$は3×4行列である。$\Theta^{(j)}$は$j+1$レイヤーのユニット数×jレイヤーのユニット数+1の行列である。まとめると以下のように表される。
\Theta^{(j)}=S_{j+1}×(S_j+1)
ベクトル化
以下のように、$z_k^{(j)}$を定義する。
a^{(2)}_1=g(z^{(2)}_1)\\
a^{(2)}_2=g(z^{(2)}_2)\\
a^{(2)}_3=g(z^{(2)}_3)
その時,
j=2レイヤーのkノードの変数zは以下のようになる。
z^{(2)}_k=\Theta^{(1)}_{k,0}x_0+\Theta^{(1)}_{k,1}x_1+⋯+\Theta^{(1)}_{k,n}x_n
ベクトルで表すと
\begin{align}
x&=
\begin{bmatrix}
x_0\\
x_1\\
...\\
x_n
\end{bmatrix}\\
z^{(j)}&=
\begin{bmatrix}
z^{(j)}_1\\
z^{(j)}_2\\
...\\
z^{(j)}_n
\end{bmatrix}\\
\end{align}\\
$x=a^{(i)}$とおくと、ベクトル$z^{(j)}$を得られる
z^{(j)}=\Theta^{(j−1)}a^{(j−1)}
これで以下のようにしてレイヤーjの活性化ノードのベクトルが得られる
a^{(j)}=g(z^{(j)})
最終的な仮説関数を得るために次のレイヤーを計算する
z^{(j+1)}=\Theta^{(j)}a^{(j)}
$\Theta^{(j)}$は1行、$a^{(j)}$は1列になるため、最終的には単数になる。
h\theta(x)=a^{(j+1)}=g(z^{(j+1)})
最後のステップでjレイヤーとj+1レイヤーの間では、ロジスティック回帰と全く同じことが行われていることがわかる。
なぜニューラルネットワークが複雑で非線形な仮説を学習するのに用いることができるのか
例えば、$x_1ANDx_2$を予測したい。$AND$は論理演算子である。視覚的には以下のように表される。
\begin{align}
&x_0\\
&x_1 \rightarrow g(z^{(2)}) \rightarrow h\theta(x) \\
&x_2
\end{align}
$x_0$はバイアスユニットで常に$1$
重み行列$\Theta$を以下のように定義する。
$$
\Theta^{(1)}=\begin{bmatrix}-30&20&20\end{bmatrix}
$$
これにより仮説の出力は$x_1$と$x_2$の両方が$1$の時、$1$となる。
$$
\begin{align}
h\theta(x)&=g(−30+20x_1+20x_2)\
x_1&=0\hspace{4pt}and\hspace{4pt}x_2=0\hspace{4pt}then\hspace{4pt}g(−30)\approx0\
x_1&=0\hspace{4pt}and\hspace{4pt}x_2=1\hspace{4pt}then\hspace{4pt}g(−10)\approx0\
x_1&=1\hspace{4pt}and\hspace{4pt}x_2=0\hspace{4pt}then\hspace{4pt}g(−10)\approx0\
x_1&=1\hspace{4pt}and\hspace{4pt}x_2=1\hspace{4pt}then\hspace{4pt}g(10)\approx1\
\end{align}
$$
このようにニューラルネットワークでANDゲートを表すことができる。NORゲートやORゲートも同じように表すことができる。整理すると以下のようになる。
$$
\begin{align}
AND:\Theta^{(1)}&=\begin{bmatrix}-30&20&20\end{bmatrix}\
NOR:\Theta^{(1)}&=\begin{bmatrix}10&-20&-20\end{bmatrix}\
OR:\Theta^{(1)}&=\begin{bmatrix}-10&20&20\end{bmatrix}\
\end{align}
$$
これら3つを組み合わせることで複雑なXNORゲートを表すことができる。視覚的には以下のように表される。
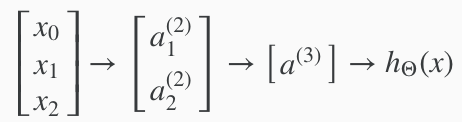
$a_1^{(2)}$はANDゲートで計算され、$a_2^{(2)}$はNANDゲートで計算され、最後の$a^{(3)}$はORゲートで計算される。すると$h_\Theta(x)$はXNORを表す。

シンプルな論理ゲートを組み合わせることでニューラルネットワーク上で複雑な論理ゲートを表すことができた。これがニューラルネットワークが複雑で非線形な仮説を学習するのに用いることができる理由である。
多クラス分類
ニューラルネットワークにおける多クラス分類も本質的にはロジスティック回帰で学んだOne vs All法と同じである。
画像を人、車、バイク、トラックの4つのうちの1つに分類する例を考える。データを複数のクラスに分類するために、仮説関数がベクトルを返すようにする。

画像の分類クラス$y^{(i)}$をそれぞれ以下のように定義することができる。

例えば、仮説関数が以下のような場合、3つ目のクラスであるバイクを表す。
$$
h_\Theta(x)=\begin{bmatrix}0\\0\\1\\0\end{bmatrix}
$$