目次と前回の記事
これまでに作成したモジュール
以下のリンクから、これまでに作成したモジュールを見ることができます。
| リンク | 説明 |
|---|---|
| marubatsu.py | Marubatsu、Marubatsu_GUI クラスの定義 |
| ai.py | AI に関する関数 |
| test.py | テストに関する関数 |
| util.py | ユーティリティ関数の定義 |
| tree.py | ゲーム木に関する Node、Mbtree クラスなどの定義 |
| gui.py | GUI に関する処理を行う基底クラスとなる GUI クラスの定義 |
AI の一覧とこれまでに作成したデータファイルについては、下記の記事を参照して下さい。
深さ制限探索の性質
下記は以前の記事で説明した深さ制限探索の性質の再掲です。
深さ制限探索 はベースとなるアルゴリズムでゲーム木の探索を行う際に、探索するノードの 深さの上限を制限 することで 処理時間を短くする代わりに、計算結果 としてが正確な値ではない 近似値 を求める ヒューリスティック なアルゴリズムです。
深さ制限探索は 一般的に下記のような性質 があります。
- 深さの上限が大きくなるほど 処理時間が増える
- 深さの上限が大きくなるほど近似値の 精度が高くなる
上記の性質から 処理時間 と 近似値の精度 は両立しない トレードオフの関係 になるため、適切な深さの上限を決めることが重要 になります。処理時間が長すぎることが大きな問題となることが多いので、一般的には制限時間の制約から深さの上限を決めることが多いのではないかと思います。
今回の記事では前回の記事で実装した、αβ 法をベースとした深さ制限探索 処理を行う ai_abs_dls を利用して 上記の性質を確認 することにします。
ミニマックス法をベースとした深さ制限探索を行う関数を実装し、それを使って確認することもできますが、ゲーム木の探索では効率の悪いミニマックス法はあまり使われないので αβ をベースとした深さ制限探索で確認することにしました。
深さの上限と処理時間の関係の確認
下記は、αβ 法をベースとした深さ制限探索を行う ai_abs_dls を利用して、下記の条件で 深さの上限を 0 ~ 9 とした場合に 計算されるノードの数を表示 するプログラムです。
-
ai14sを静的評価関数とする - ゲーム開始時の局面のミニマックス値を計算する
- 置換表を利用する場合としない場合の両方の計算を行う
from ai import ai_abs_dls, ai14s
from marubatsu import Marubatsu
mb = Marubatsu()
for use_tt in [False, True]:
print(f"use_tt: {use_tt}")
for maxdepth in range(10):
count = ai_abs_dls(mb, maxdepth=maxdepth, eval_func=ai14s, eval_params={"minimax": True},
use_tt=use_tt, calc_score=True, calc_count=True)
print(f"maxdepth: {maxdepth} count {count}")
実行結果
use_tt: False
maxdepth: 0 count 1
maxdepth: 1 count 10
maxdepth: 2 count 36
maxdepth: 3 count 171
maxdepth: 4 count 658
maxdepth: 5 count 2648
maxdepth: 6 count 7202
maxdepth: 7 count 12762
maxdepth: 8 count 15640
maxdepth: 9 count 18297
use_tt: True
maxdepth: 0 count 1
maxdepth: 1 count 10
maxdepth: 2 count 27
maxdepth: 3 count 76
maxdepth: 4 count 189
maxdepth: 5 count 413
maxdepth: 6 count 831
maxdepth: 7 count 978
maxdepth: 8 count 1049
maxdepth: 9 count 1069
実行結果から、深さの上限が増える と 深さが 6 まで は計算するノードの数が 2 倍以上の 指数関数的に増えていく ことが確認できます。また、置換表を利用 することで 効率を高めることができる ことが確認できました。なお、〇× ゲームは 着手を行うたびに合法手の数が減る ので、深さが 深くなるにつれて ノードの数の 増え方の割合が減っていきます。
次に、上記のそれぞれの場合の平均処理時間を timeit の前に % を一つだけ記述 した %timeit を利用して計測することにします。以前の記事で紹介した timeit の前に % を 二つ記述 する %%timeit は、JupyterLab の セルの中に記述 されたプログラム全体の 処理時間の平均と標準偏差を計測 しますが、%time は その後に記述 した 1 つの文 の処理時間の平均と標準偏差を計測します。
下記はそのプログラムで、先程のプログラムとの大きな違いは ai_abs_dls を呼び出す処理の 前に %timeit を記述 する点です。なお、%timeit で計測する処理の記述の途中で 改行したい場合 は 文の途中で改行する場合と同様 に 改行の直前に \ を記述 する必要があります。他の違いとしては、処理時間とは関係のない表示を行う処理は削除しました。
for use_tt in [False, True]:
print(f"use_tt: {use_tt}")
for maxdepth in range(10):
print(f"maxdepth {maxdepth}")
%timeit ai_abs_dls(mb, maxdepth=maxdepth, eval_func=ai14s, \
eval_params={"minimax": True}, use_tt=use_tt, \
calc_score=True, calc_count=True)
修正箇所
for use_tt in [False, True]:
print(f"use_tt: {use_tt}")
for maxdepth in range(10):
+ print(f"maxdepth {maxdepth}")
- count = ai_abs_dls(mb, maxdepth=maxdepth, eval_func=ai14s,
- eval_params={"minimax": True}, use_tt=use_tt,
- calc_score=True, calc_count=True)
- print(f"maxdepth: {maxdepth} count {count}")
+ %timeit ai_abs_dls(mb, maxdepth=maxdepth, eval_func=ai14s, \
+ eval_params={"minimax": True}, use_tt=use_tt, \
+ calc_score=True, calc_count=True)
実行結果
use_tt: False
maxdepth 0
21.8 µs ± 854 ns per loop (mean ± std. dev. of 7 runs, 10,000 loops each)
maxdepth 1
524 µs ± 3.4 µs per loop (mean ± std. dev. of 7 runs, 1,000 loops each)
maxdepth 2
1.97 ms ± 96.3 µs per loop (mean ± std. dev. of 7 runs, 100 loops each)
maxdepth 3
9.74 ms ± 12.3 µs per loop (mean ± std. dev. of 7 runs, 100 loops each)
maxdepth 4
38.6 ms ± 98 µs per loop (mean ± std. dev. of 7 runs, 10 loops each)
maxdepth 5
152 ms ± 612 µs per loop (mean ± std. dev. of 7 runs, 10 loops each)
maxdepth 6
412 ms ± 1.57 ms per loop (mean ± std. dev. of 7 runs, 1 loop each)
maxdepth 7
691 ms ± 2.14 ms per loop (mean ± std. dev. of 7 runs, 1 loop each)
maxdepth 8
831 ms ± 10 ms per loop (mean ± std. dev. of 7 runs, 1 loop each)
maxdepth 9
902 ms ± 4.17 ms per loop (mean ± std. dev. of 7 runs, 1 loop each)
use_tt: True
maxdepth 0
21.6 µs ± 372 ns per loop (mean ± std. dev. of 7 runs, 10,000 loops each)
maxdepth 1
544 µs ± 2.18 µs per loop (mean ± std. dev. of 7 runs, 1,000 loops each)
maxdepth 2
1.47 ms ± 2.79 µs per loop (mean ± std. dev. of 7 runs, 1,000 loops each)
maxdepth 3
4.32 ms ± 10.2 µs per loop (mean ± std. dev. of 7 runs, 100 loops each)
maxdepth 4
11.4 ms ± 184 µs per loop (mean ± std. dev. of 7 runs, 100 loops each)
maxdepth 5
24.9 ms ± 921 µs per loop (mean ± std. dev. of 7 runs, 10 loops each)
maxdepth 6
50.2 ms ± 515 µs per loop (mean ± std. dev. of 7 runs, 10 loops each)
maxdepth 7
58.1 ms ± 1.67 ms per loop (mean ± std. dev. of 7 runs, 10 loops each)
maxdepth 8
60.1 ms ± 200 µs per loop (mean ± std. dev. of 7 runs, 10 loops each)
maxdepth 9
59.8 ms ± 168 µs per loop (mean ± std. dev. of 7 runs, 10 loops each)
下記は上記の結果をまとめた表です。表の平均処理時間を回数で割った 1 回あたりの平均処理時間 が、深さの上限が 0 以外の場合で置換表を利用しない場合とする場合の両方で平均である 約 53 μs と 約 58 μs に 近い値になっている ことから、処理時間 が計算した ノードの数にほぼ比例する ことが確認できます。なお、深さの上限が 0 の場合の平均処理時間が短い理由はおそらく子ノードの評価値を比較する処理が必要ないからだと思います。また、置換表を利用する場合は置換表に関する処理を行う分だけ平均処理時間が長くなります。
置換表を利用しない場合
| 深さの上限 | 回数 | 平均処理時間(ms) | 1 回あたりの平均処理時間(μs) |
|---|---|---|---|
| 0 | 1 | 0.0218 | 21.8 |
| 1 | 10 | 0.524 | 52.4 |
| 2 | 36 | 1.97 | 54.7 |
| 3 | 171 | 9.74 | 57.0 |
| 4 | 658 | 38.6 | 58.7 |
| 5 | 2648 | 152 | 57.4 |
| 6 | 7202 | 412 | 57.2 |
| 7 | 12762 | 691 | 54.1 |
| 8 | 15640 | 831 | 53.1 |
| 9 | 18297 | 902 | 49.3 |
| 合計 | 57425 | 3039 | 52.9 |
置換表を利用する場合
| 深さの上限 | 回数 | 平均処理時間(ms) | 1 回あたりの平均処理時間(μs) |
|---|---|---|---|
| 0 | 1 | 0.0216 | 21.6 |
| 1 | 10 | 0.544 | 54.4 |
| 2 | 27 | 1.47 | 54.4 |
| 3 | 76 | 4.32 | 56.8 |
| 4 | 189 | 11.4 | 60.3 |
| 5 | 413 | 24.9 | 60.3 |
| 6 | 831 | 50.2 | 60.4 |
| 7 | 978 | 58.1 | 59.4 |
| 8 | 1049 | 60.1 | 57.3 |
| 9 | 1069 | 59.8 | 55.0 |
| 合計 | 4643 | 269.9 | 58.1 |
上記から下記の事が確認できました。
深さ制限探索 の 処理時間 は、計算する ノードの数に比例 する。
従って、ノードの数が 深さに対して指数関数的に増えるゲーム木 の 深さ制限探索 による 処理時間 は、深さの上限 に対して 指数関数的に増える。
〇×ゲームでの深さの上限と精度の関係
〇×ゲーム での 深さ制限探索 によって計算された ミニマックス値の近似値 の 精度 と、深さの上限の関係 について検証することにします。
深さの上限が 0 の場合に行われる処理
深さの上限を 0 とした深さ制限探索による ミニマックス値の近似値の計算 は、深さが 0 の ルートノードの局面 に対して 静的評価関数が計算した評価値 になります。従って、ai_abs_dls にキーワード引数 maxdepth=0 と calc_score=True を記述して呼び出すと、キーワード引数 eval_func で指定した 評価関数が計算した評価値 が返されます。
深さの上限を 0 とした深さ制限探索によって計算されるミニマックス値の近似値の 精度 は、深さ制限探索で利用する 静的評価関数と同じ になる。
そのことを、AI どうしの通算成績を計算 する ai_match を利用した下記の処理を行うことで 確認する ことにします。下記では 3 種類の静的評価関数で確認を行なっていますが、余裕がある方は他の評価関数でも確認を行なってみて下さい。
-
静的評価関数を
ai2s、深さの上限を 0 としたai_ab_dlsVSai2sとの対戦をai_matchを利用して 1000 回行う -
ai2sVSai2sとの対戦をai_matchを利用して 1000 回行い、上記の通算成績とほぼ同じになる ことを確認する -
静的評価関数 を
ai10s、ai14sとした場合で 上記と同様の対戦 を行ない、通算成績がほぼ同じになる ことを確認する
ai_abs_dls が行う処理を正しく理解している人にとっては両者が同じ処理を行うことは明らかなので、このような確認を行うことに意味がないと思う人がいるかもしれませんが、実際に実行して結果に差がないことを確認 することで、ai_abs_dls が少なくとも 深さの上限を 0 とした場合の 処理を正しく実装できている ことを 確認できる という意味があります。
下記はそのプログラムです。
-
3 行目:
ai_abs_dlsを呼び出す際の実引数を表す dict をparamsに代入する - 4 行目:3 つの静的評価関数に対する繰り返し処理を行う
-
5 行目:静的評価関数の名前を表示する。なお、関数の名前は特殊属性
__name__に代入されている -
6 行目:
paramsの"eval_func"のキーに静的評価関数を代入する -
7 行目:
ai_abs_dlsVSai2sの対戦を 1000 回行う -
8 行目:静的評価関数
eval_funcVSai2sの対戦を 1000 回行う
1 from ai import ai_match, ai2s, ai10s
2
3 params = {"maxdepth": 0, "eval_func": ai2s, "eval_params": {"minimax": True}}
4 for eval_func in [ai2s, ai10s, ai14s]:
5 print(f"eval_func {eval_func.__name__}")
6 params["eval_func"] = eval_func
7 ai_match(ai=[ai_abs_dls, ai2s], params=[params, {}], match_num=1000)
8 ai_match(ai=[eval_func, ai2s], match_num=1000)
行番号のないプログラム
from ai import ai_match, ai2s, ai10s
params = {"maxdepth": 0, "eval_func": ai2s, "eval_params": {"minimax": True}}
for eval_func in [ai2s, ai10s, ai14s]:
print(f"eval_func {eval_func.__name__}")
params["eval_func"] = eval_func
ai_match(ai=[ai_abs_dls, ai2s], params=[params, {}], match_num=1000)
ai_match(ai=[eval_func, ai2s], match_num=1000)
実行結果
100%|██████████| 1000/1000 [00:06<00:00, 148.24it/s]
count win lose draw
o 592 275 133
x 277 597 126
total 869 872 259
ratio win lose draw
o 59.2% 27.5% 13.3%
x 27.7% 59.7% 12.6%
total 43.5% 43.6% 13.0%
ai2s VS ai2s
100%|██████████| 1000/1000 [00:06<00:00, 159.47it/s]
count win lose draw
o 591 291 118
x 284 597 119
total 875 888 237
ratio win lose draw
o 59.1% 29.1% 11.8%
x 28.4% 59.7% 11.9%
total 43.8% 44.4% 11.8%
eval_func ai10s
ai_abs_dls VS ai2s
100%|██████████| 1000/1000 [00:07<00:00, 139.58it/s]
count win lose draw
o 970 0 30
x 847 29 124
total 1817 29 154
ratio win lose draw
o 97.0% 0.0% 3.0%
x 84.7% 2.9% 12.4%
total 90.8% 1.5% 7.7%
ai10s VS ai2s
100%|██████████| 1000/1000 [00:06<00:00, 146.69it/s]
count win lose draw
o 976 0 24
x 852 20 128
total 1828 20 152
ratio win lose draw
o 97.6% 0.0% 2.4%
x 85.2% 2.0% 12.8%
total 91.4% 1.0% 7.6%
eval_func ai14s
ai_abs_dls VS ai2s
100%|██████████| 1000/1000 [00:07<00:00, 138.40it/s]
count win lose draw
o 988 0 12
x 884 0 116
total 1872 0 128
ratio win lose draw
o 98.8% 0.0% 1.2%
x 88.4% 0.0% 11.6%
total 93.6% 0.0% 6.4%
ai14s VS ai2s
100%|██████████| 1000/1000 [00:06<00:00, 160.48it/s]
count win lose draw
o 988 0 12
x 892 0 108
total 1880 0 120
ratio win lose draw
o 98.8% 0.0% 1.2%
x 89.2% 0.0% 10.8%
total 94.0% 0.0% 6.0%
実行結果から 通算成績がほぼ同じである ことが実際に確認できました。
深さの上限を増やした場合の AI の通算成績の計算
ミニマックス値の近似値の 精度が高まる と、正確なミニマックス値 が計算される 可能性が高まる ので 強解決の AI に近づきます。そのため、ai_match を使ってランダムな AI である ai2s と対戦した際の通算成績を比べる ことで、近似値の精度を測る ことができます。
〇× ゲーム は ゲーム開始時 の局面の 状態が引き分け なので、近似値の 精度が高いほど ai2s との通算成績の 敗率が 0 % に近づき、敗率が 0 % になった時点で ai2s との対戦で生じる局面に対するミニマックス値の近似値の 精度が 100 % だとみなすことができます。
ai2s はランダムな着手を行うので、充分な回数の対戦 を行わないと敗率が 0 % になったとしても精度が 100 % になったとみなすことはできません。今回の記事では 1000 回対戦を行うことにしました。
また、ai2s との対戦で発生しない局面のミニマックス値の精度は判定できないので、その場合 弱解決の AI であることは判定できますが、強解決の AI であることは判定できません。強解決の AI であるかどうかの判定は Check_solved で行います。
そこで、下記の 様々な異なる精度 の静的評価関数を使って、深さの上限を 0 から 81 まで増やした場合の ai_abs_dls VS ai2s の対戦を行うことにします。興味がある方は他の AI でも同様の計算を行ってみて下さい。
- すべての局面で評価値として 0 を計算する、ランダムな着手を行う
ai2s - 真ん中のマスを優先的に着手する
ai3s - 自分が勝利している場合に 1、そうでない場合に 0 を計算する
ai5s - 弱解決ではないが、それなりに高い精度で近似値を計算する
ai10s - 弱解決で、対戦においては精度が 100 % のミニマックス値を計算する
ai14s
ai_match の修正
現状の ai_match は 通算成績を画面に表示するだけ で返り値として返さないので、後から通算成績を利用 することは できません。そこで、下記のプログラムのように、通算成績を返り値として返す ように ai_match を修正することにします。
-
9 行目:通算成績に関するデータは 7 行目で
diff_listに代入されるので、それを返り値として返すように修正する
1 from collections import defaultdict
2 from tqdm import tqdm
3
4 def ai_match(ai, params, match_num=10000):
元と同じなので省略
5 # 通算成績の回数と比率の表示
6 width = max(len(str(match_num * 2)), 7)
7 diff_list = [ ("count", count_list_ai0, f"{width}d"),
8 ("ratio", ratio_list, f"{width}.1%") ]
元と同じなので省略
9 return diff_list
行番号のないプログラム
from collections import defaultdict
from tqdm import tqdm
def ai_match(ai, params, match_num=10000):
print(f"{ai[0].__name__} VS {ai[1].__name__}")
mb = Marubatsu()
# ai[0] VS ai[1] と ai[1] VS a[0] の対戦を match_num 回行い、通算成績を数える
count_list = [ defaultdict(int), defaultdict(int)]
for _ in tqdm(range(match_num)):
count_list[0][mb.play(ai, params=params, verbose=False)] += 1
count_list[1][mb.play(ai=ai[::-1], params=params[::-1], verbose=False)] += 1
# ai[0] から見た通算成績を計算する
count_list_ai0 = [
# ai[0] VS ai[1] の場合の、ai[0] から見た通算成績
{
"win": count_list[0][Marubatsu.CIRCLE],
"lose": count_list[0][Marubatsu.CROSS],
"draw": count_list[0][Marubatsu.DRAW],
},
# ai[1] VS ai[0] の場合の、ai[0] から見た通算成績
{
"win": count_list[1][Marubatsu.CROSS],
"lose": count_list[1][Marubatsu.CIRCLE],
"draw": count_list[1][Marubatsu.DRAW],
},
]
# 両方の対戦の通算成績の合計を計算する
count_list_ai0.append({})
for key in count_list_ai0[0]:
count_list_ai0[2][key] = count_list_ai0[0][key] + count_list_ai0[1][key]
# それぞれの比率を計算し、ratio_list に代入する
ratio_list = [ {}, {}, {} ]
for i in range(3):
for key in count_list_ai0[i]:
ratio_list[i][key] = count_list_ai0[i][key] / sum(count_list_ai0[i].values())
# 各行の先頭に表示する文字列のリスト
item_text_list = [ Marubatsu.CIRCLE, Marubatsu.CROSS, "total" ]
# 通算成績の回数と比率の表示
width = max(len(str(match_num * 2)), 7)
diff_list = [ ("count", count_list_ai0, f"{width}d"),
("ratio", ratio_list, f"{width}.1%") ]
for title, data, format in diff_list:
print(title, end="")
for key in data[0]:
print(f" {key:>{width}}", end="")
print()
for i in range(3):
print(f"{item_text_list[i]:5}", end="")
for value in data[i].values():
print(f" {value:{format}}", end="")
print()
print()
return diff_list
修正箇所
from collections import defaultdict
from tqdm import tqdm
def ai_match(ai, params, match_num=10000):
元と同じなので省略
# 通算成績の回数と比率の表示
width = max(len(str(match_num * 2)), 7)
diff_list = [ ("count", count_list_ai0, f"{width}d"),
("ratio", ratio_list, f"{width}.1%") ]
元と同じなので省略
+ return diff_list
対戦を行うプログラムの実行
下記は ai2s、ai3s、ai5s、ai10s、ai14s を 静的評価関数 とした ai_ab_dls VS ai2s の対戦を、深さの上限が 0 から 8 までのそれぞれの場合で行うプログラムです。
それぞれの AI との 通算成績 は 下記のデータ構造で記録 することにします。
- 全体を dict で記録する
- 上記の dict の AI の関数名のキーの値に、その AI を静的評価関数とした場合の通算成績を list で記録する
- 上記の list には深さの上限ごとの通算成績を順番に記録する
例えば ai2s を静的評価関数とし、深さの上限を 2 とした場合の通算成績は、全体のデータを表す dict を result という変数に代入した場合は、result["ai2s"][2] に記録されます。
なお、置換表を利用しないと処理時間がかなり長くなるので置換表を利用しています。また、通算成績の精度を上げるため に 対戦回数を 1000 回 としました。そのため下記のプログラムの処理は筆者のパソコンでは 1 時間半ほど かかりました。
-
3 行目:それぞれの通算成績を記録する
resultという変数を空の dict で初期化する -
4 行目:
ai_abs_dlsを呼び出す際に記述する実引数を表すparamsを初期化する - 5 行目:それぞれの AI の関数に対する繰り返し処理を行う
-
6 行目:
paramsの中で静的評価関数を表すキーの値を設定する -
7、8 行目:静的評価関数の名前を
nameに代入し、その静的評価関数を利用した場合の深さの上限ごとの通算成績を記録するresult[name]を空の list で初期化する -
10 行目:
paramsの中で深さの上限を表すキーの値を設定する -
11、12 行目:
ai_matchで対戦を行い、通算成績をdiff_listに代入する -
13 行目:
result[name]の list の要素に通算成績を追加する
1 from ai import ai3s, ai5s
2
3 result = {}
4 params = {"maxdepth": 0, "eval_func": ai2s, "eval_params": {"minimax": True}}
5 for eval_func in [ai2s, ai3s, ai5s, ai10s, ai14s]:
6 params["eval_func"] = eval_func
7 name = eval_func.__name__
8 result[name] = []
9 for maxdepth in range(9):
10 print(f"{name} maxdepth: {maxdepth}")
11 params["maxdepth"] = maxdepth
12 diff_list = ai_match(ai=[ai_abs_dls, ai2s], params=[params, {}], match_num=1000)
13 result[name].append(diff_list)
行番号のないプログラム
from ai import ai3s, ai5s
result = {}
params = {"maxdepth": 0, "eval_func": ai2s, "eval_params": {"minimax": True}}
for eval_func in [ai2s, ai3s, ai5s, ai10s, ai14s]:
params["eval_func"] = eval_func
name = eval_func.__name__
result[name] = []
for maxdepth in range(9):
print(f"{name} maxdepth: {maxdepth}")
params["maxdepth"] = maxdepth
diff_list = ai_match(ai=[ai_abs_dls, ai2s], params=[params, {}], match_num=1000)
result[name].append(diff_list)
実行結果
ai2s maxdepth: 0
ai_abs_dls VS ai2s
100%|██████████| 1000/1000 [00:06<00:00, 160.04it/s]
count win lose draw
o 568 292 140
x 301 569 130
total 869 861 270
ratio win lose draw
o 56.8% 29.2% 14.0%
x 30.1% 56.9% 13.0%
total 43.5% 43.0% 13.5%
ai2s maxdepth: 1
ai_abs_dls VS ai2s
100%|██████████| 1000/1000 [00:18<00:00, 54.30it/s]
count win lose draw
o 593 271 136
x 293 563 144
total 886 834 280
ratio win lose draw
o 59.3% 27.1% 13.6%
x 29.3% 56.3% 14.4%
total 44.3% 41.7% 14.0%
略
グラフによる視覚化
上記の通算成績を 表でまとめても 大量の数字が並ぶだけで わかりづらい ので、下記のプログラムを実行して グラフで視覚化 することにします。なお、x 軸の下と y 軸の左に表示するラベル(説明のこと)は xlabel、ylabel というメソッドで表示することができます。
- 3 行目:勝率、敗率、引分率のそれぞれに対するグラフの描画の繰り返し処理を行う
- 4 行目:それぞれの静的評価関数に対する繰り返し処理を行う
-
5 行目:深さの上限ごとの比率(ratio)を記録する
ratioを空の list で初期化する -
6、7 行目:比率のデータは
diff_list[1][1][2][type]に代入されているので、それをratioに代入された list の要素に追加する。diff_listについて忘れた方は以前の記事を復習すること - 8 行目:静的評価関数の名前のラベルをつけて比率を折れ線グラフで表示する
- 9、10 行目:x 軸と y 軸のラベルを表示する
- 11 行目:グラフの凡例を描画する。凡例とラベルについて忘れた方は 以前の記事を復習すること
-
12 行目:
plt.show()を実行してグラフを描画する。これを実行しないと、勝率、敗率、引分率のグラフが 1 つのグラフで表示されてしまう
1 import matplotlib.pyplot as plt
2
3 for type in ["win", "lose", "draw"]:
4 for name, value in result.items():
5 ratio = []
6 for diff_list in value:
7 ratio.append(diff_list[1][1][2][type])
8 plt.plot(ratio, label=f"{name}")
9 plt.xlabel("max depth")
10 plt.ylabel(f"{type} ratio")
11 plt.legend()
12 plt.show()
行番号のないプログラム
import matplotlib.pyplot as plt
for type in ["win", "lose", "draw"]:
for name, value in result.items():
ratio = []
for diff_list in value:
ratio.append(diff_list[1][1][2][type])
plt.plot(ratio, label=f"{name}")
plt.xlabel("max depth")
plt.ylabel(f"{type} ratio")
plt.legend()
plt.show()
実行結果
勝率のグラフ
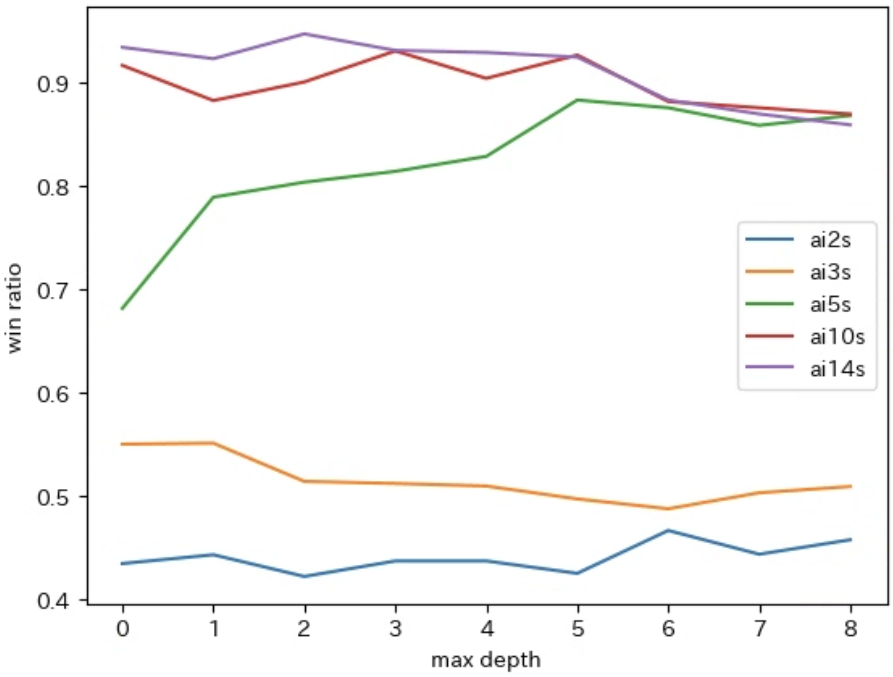
敗率のグラフ
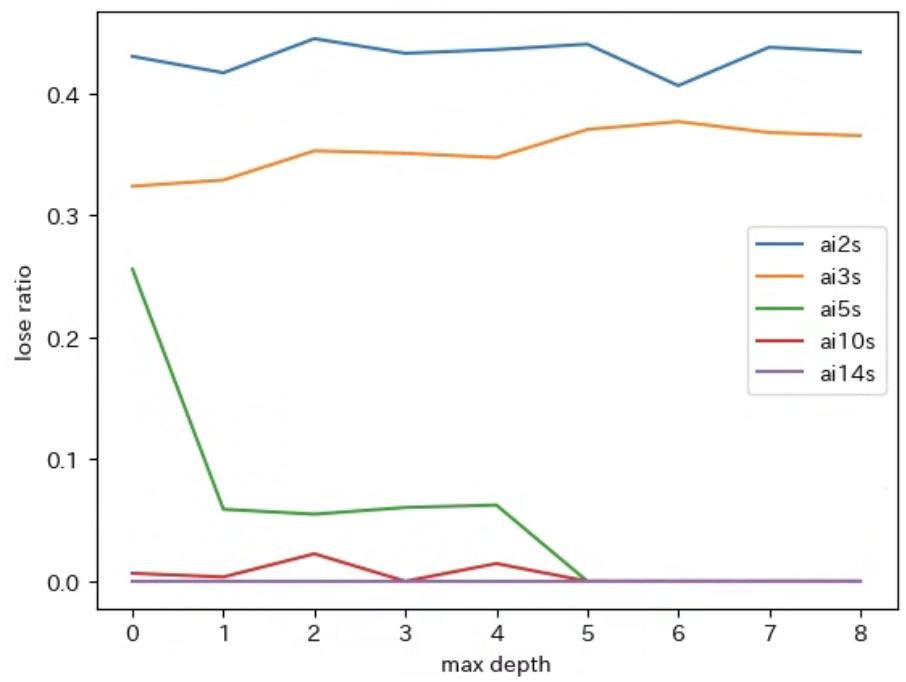
引分率のグラフ

実行結果の考察
上記の実行結果を 静的評価関数ごとに考察 します。
ai2s の場合
実行結果のグラフから ai2s を静的評価関数とした場合は、深さの上限を増やしても 通算成績がほとんど変わらない ことが確認できます。これは、ai2s が決着がついたリーフノードを含めて 常に局面の評価値として 0 を計算 するため、深さの上限に関わらす すべての局面の評価値が 0 として計算された結果 ランダムな着手を行う からです。
このことから 静的評価関数 が計算するミニマックス値の近似値の 精度が低すぎる場合 は、深さ制限探索で深さの上限を増やしても近似値の 精度は向上しない ことがわかります。
ai3s の場合
ai3s を静的評価関数とした場合は下記のような評価値を計算します。その結果、ai3s は真ん中のマスに優先的に着手 を行います。なお、以後の説明ではキーワード引数に minimax=True を記述して ミニマックス値の近似値 を計算した場合の説明を行います。
- 直前の着手が真ん中の (1, 1) の場合は以下の計算を行う
- (1, 1) に 〇 が着手した場合は 1 を計算する
- (1, 1) に × が着手した場合は -1 を計算する
- そうでなければ 0 を計算する
実行結果のグラフから ai3s を静的評価関数とした場合の 通算成績 は、ai2s を静的評価関数とした場合 よりも良い ので、ai3s は ai2s よりも精度が高い近似値 を計算すると考えることができます。しかし、実行結果のグラフから ai3s を静的評価関数とした場合も、深さの上限を増やしても 通算成績が ほとんど変わらない ことが確認できます。その理由について少し考えてみて下さい。
その理由の一つは、ゲーム開始時の局面 に対して 深さの上限を 2 以上 とした場合に、下記の理由から ai3s が ランダムな着手を行う からです。
ゲーム開始時の局面 に対して、深さの上限を $\boldsymbol{d}$ として ai_abs_dls の計算を行うと、下記のような処理が行われます。
- ゲーム開始時の局面は max ノード なので、合法手を着手した子ノードの局面中で 最も評価値が高い 合法手の中からランダムで着手を行う
- ルートノードの 子ノードを $\boldsymbol{C}$ と表記した場合に、$C$ の局面の評価値は 深さの上限を $\boldsymbol{d}$ とする深さ制限探索で計算する
深さの上限を 0 とした場合はルートノードの 子ノードの評価値 を静的評価関数 ai3s で計算 します。従って (1, 1) に着手を行った 子ノードの 評価値が 1、それ以外 の子ノードの 評価値 が 0 になるので、(1, 1) のみが選択 されます。そのことは、下記のプログラムから確認することができます。
from pprint import pprint
mb = Marubatsu()
pprint(ai_abs_dls(mb, eval_func=ai3s, eval_params={"minimax":True}, maxdepth=0, analyze=True))
実行結果
{'candidate': [(1, 1)],
'score_by_move': {(0, 0): 0,
(0, 1): 0,
(0, 2): 0,
(1, 0): 0,
(1, 1): 1,
(1, 2): 0,
(2, 0): 0,
(2, 1): 0,
(2, 2): 0}}
深さの上限を 1 とした場合は下記の計算が行われた結果、(1, 1) に着手 を行った子ノードの 評価値が 0、それ以外 の子ノードの 評価値が -1 になるので (1, 1) のみが選択 されます。
- ゲーム開始時の局面で (1, 1) に着手を行った場合 の子ノード $C$ の評価値は、下記の理由から 0 が計算 される
- $C$ の 合法手 には (1, 1) は存在しない ので、$\boldsymbol{C}$ の子ノード に 直前の着手が (1, 1) である局面は 存在しない
- 従って、$C$ の すべての子ノードの評価値は 0 が計算される
- ゲーム開始時の局面で (1, 1) 以外 に着手を行った場合の子ノード $C$ の評価値は、下記の理由から -1 が計算 される
- $C$ の 子ノード の中で 直前の着手が (1, 1) の場合の 評価値は -1 が計算される
- それ以外 の子ノードの 評価値は 0 が計算される
- $\boldsymbol{C}$ は min ノード なので子ノードの評価値の 最小値である -1 が計算 される
そのことは、下記のプログラムから確認することができます。
pprint(ai_abs_dls(mb, eval_func=ai3s, eval_params={"minimax":True}, maxdepth=1, analyze=True))
実行結果
{'candidate': [(1, 1)],
'score_by_move': {(0, 0): -1,
(0, 1): -1,
(0, 2): -1,
(1, 0): -1,
(1, 1): 0,
(1, 2): -1,
(2, 0): -1,
(2, 1): -1,
(2, 2): -1}}
深さの上限を 2 とした場合は、下記の計算が行われた結果 すべての子ノードの 評価値が 0 となるため合法手の中から ランダムな着手 が行われます。
- ゲーム開始時の局面で (1, 1) に着手を行った場合 の子ノード $C$ の評価値は、下記の理由から 0 が計算 される
- $\boldsymbol{C}$ の 深さが 2 以上 の子孫ノードには、直前の着手が (1, 1) である局面が 存在しない
- 従って、$C$ の 深さが 2 の子孫ノード の評価値は すべて 0 が計算 される
- 従って、$C$ の 深さが 1 の子ノード の評価値は すべて 0 が計算 される
- 従って、$\boldsymbol{C}$ の評価値は 0 が計算される
- ゲーム開始時の局面で (1, 1) 以外 に着手を行った場合の子ノード $C$ の評価値も、下記の理由から 0 が計算 される
- $C$ には (1, 1) と それ以外 の 合法手 が存在し、$C$ の子ノードを $G$ と表記すると $\boldsymbol{G}$ の評価値 は 深さの上限を 1 とした 深さ制限探索 によって計算される
- max ノートと min ノードの違いはあるが、先程の 深さの上限を 1 とした場合の 検証と同じ理由 から、$G$ の評価値は下記のように計算される。そのことは、下記のプログラムから確認することができる
- $C$ の局面で (1, 1) に着手 を行った場合の 評価値は 0 となる
- $C$ の局面で (1, 1) 以外 に着手を行った場合の 評価値は 1 となる
- $\boldsymbol{C}$ は min ノード なのでその 評価値は 0 が計算 される
mb.move(0, 0)
pprint(ai_abs_dls(mb, eval_func=ai3s, eval_params={"minimax":True}, maxdepth=1, analyze=True))
実行結果
{'candidate': [(1, 1)],
'score_by_move': {(0, 1): 1,
(0, 2): 1,
(1, 0): 1,
(1, 1): 0,
(1, 2): 1,
(2, 0): 1,
(2, 1): 1,
(2, 2): 1}}
深さの上限を 2 とした場合に すべての子ノードの評価値が 0 と計算され、ランダムな着手 が行われることは下記のプログラムで確認することができます。
mb.restart()
pprint(ai_abs_dls(mb, eval_func=ai3s, eval_params={"minimax":True}, maxdepth=2, analyze=True))
実行結果
{'candidate': [(0, 0),
(1, 0),
(2, 0),
(0, 1),
(1, 1),
(2, 1),
(0, 2),
(1, 2),
(2, 2)],
'score_by_move': {(0, 0): 0,
(0, 1): 0,
(0, 2): 0,
(1, 0): 0,
(1, 1): 0,
(1, 2): 0,
(2, 0): 0,
(2, 1): 0,
(2, 2): 0}}
厳密な証明は省略しますが、深さの上限 3 以上の場合 も深さの上限が 2 以上の場合と同様の理由から、すべての子ノードの評価値が 0 と計算され ランダムな着手 が行われます。そのことは下記のプログラムを実行することで確認できます。
for maxdepth in range(9):
result = ai_abs_dls(mb, eval_func=ai3s, eval_params={"minimax":True},
maxdepth=maxdepth, analyze=True)
print(f"maxdepth {maxdepth}")
print(f"candidate {result['candidate']}")
実行結果
maxdepth 0
candidate [(1, 1)]
maxdepth 1
candidate [(1, 1)]
maxdepth 2
candidate [(0, 0), (1, 0), (2, 0), (0, 1), (1, 1), (2, 1), (0, 2), (1, 2), (2, 2)]
maxdepth 3
candidate [(0, 0), (1, 0), (2, 0), (0, 1), (1, 1), (2, 1), (0, 2), (1, 2), (2, 2)]
maxdepth 4
candidate [(0, 0), (1, 0), (2, 0), (0, 1), (1, 1), (2, 1), (0, 2), (1, 2), (2, 2)]
maxdepth 5
candidate [(0, 0), (1, 0), (2, 0), (0, 1), (1, 1), (2, 1), (0, 2), (1, 2), (2, 2)]
maxdepth 6
candidate [(0, 0), (1, 0), (2, 0), (0, 1), (1, 1), (2, 1), (0, 2), (1, 2), (2, 2)]
maxdepth 7
candidate [(0, 0), (1, 0), (2, 0), (0, 1), (1, 1), (2, 1), (0, 2), (1, 2), (2, 2)]
maxdepth 8
candidate [(0, 0), (1, 0), (2, 0), (0, 1), (1, 1), (2, 1), (0, 2), (1, 2), (2, 2)]
上記の説明から、深さの上限を 2 以上とした場合の通算成績は深さの上限を 0、1 とした場合よりも減ると思った方がいるかもしれませんが、おそらく下記のような理由から ai2s よりも精度の高い近似値を計算できる ので、通算成績はそれほど変わらないようです。
-
ai3sは、(1, 1) に着手 を行うことで ゲームの決着がついた局面 では 正しいミニマックス値を計算 することができる - 深さの上限が大きくなる と 決着がついた局面 の評価値を計算することが 多くなる
-
ランダムな着手を行う
ai2sとの対戦 の場合2は (1, 1) に着手を行う ことで 決着がつく局面が存在する
ai5s の場合
ai5s は以下のような評価値を計算する静的評価関数で、ai5s は 勝利できる場合に勝利する 着手を行います。
- 〇 が勝利している場合は 1 を計算する
- × が勝利している場合は -1 を計算する
- それ以外の場合は 0 を計算する
下記は勝率と敗率のグラフの再掲です。引分率は重要ではないので省略しました。
勝率のグラフ

敗率のグラフ

実行結果のグラフから ai5s を静的評価関数とした深さ制限探索の AI は、深さの上限を 増やすほど通算成績が向上する ことがわかります。
深さの上限を 1 とした場合の 通算成績 が向上する理由は、その場合に行われる処理が 勝利できる場合に勝利 し、相手が次の手番で勝利できる場合は 相手の勝利を妨害 する ai6s と同じになるからです。下記の表の ai_abs_dls の行 は先程行った静的評価関数を ai5s、深さの上限を 1 とした場合の対戦結果です。ai6s の行 は以前の記事で行った ai6s VS ai2s の対戦結果で、実際に 両者がほぼ同じである ことが確認できます。
静的評価関数を ai5s、深さの上限を 1 とした ai_abs_dls で行われる処理が ai6s と同じ になる理由について少し考えてみて下さい。
| 関数名 | o 勝 | o 負 | o 分 | x 勝 | x 負 | x 分 | 勝 | 負 | 分 |
|---|---|---|---|---|---|---|---|---|---|
ai_abs_dls |
89.4 | 2.8 | 7.8 | 68.4 | 9.0 | 22.6 | 78.9 | 5.9 | 15.2 |
ai6s |
88.6 | 1.9 | 9.5 | 69.4 | 9.1 | 21.5 | 79.0 | 5.5 | 15.5 |
深さの上限を 1 とした場合は、現在の局面に対して自分と相手が着手した 2 手先の局面の評価値 を ai5s で計算 します。その結果、〇 の手番 の局面に対する処理は下記のように計算されます。なお、× の手番の局面の場合は同様なので説明を省略します。
- それぞれの 子ノードの評価値 を下記のように計算する
- 自分が勝利している局面の評価値は 1
- 次の相手の手番で相手が勝利できる合法手が存在する場合の評価値は -1
- そうでなければ 0
- 〇 の手番の局面は max ノード なので 最も高い評価値の子ノード の合法手が選択され、下記の優先順位で着手が選択される。これは
ai6sが選択する着手と同じ ものである- 自分が勝利する合法手
- 次の相手の勝利を妨害する合法手
- それ以外の合法手
深さの上限を 0 とした場合の ai5s は、次の自分の着手のみを考慮 しますが、深さの上限を 1 とした場合の ai5s は その次の相手の着手も考慮 するため より強くなります。
深さの上限を 2 以上とした場合はより先の局面を考慮するためさらに強くなります。
また、実行結果のグラフから 深さの上限が 5 以上 になると 敗率が 0 になることから、弱解決の AI と同じ強さ を持つようになることがわかります。さらに、深さの上限を最大の 8 にすると ai10s や ai14s と同じ通算成績 になることもわかります。
ai2s と ai3s が深さの上限を増やしても 精度が上がらず、ai5s の場合は 精度が上がる理由 についてはこの後で説明します。その理由について少し考えてみて下さい。
ai10s と ai14s の場合
ai10s は 弱解決ではありません が、ai2s との 通算成績の勝率が 約 90 % なので計算する 近似値の精度はかなり高い と考えられます。また、実行結果のグラフから ai10s を静的評価関数とした場合は 深さの上限を上げる と下記のような性質を持つことがわかります。
-
最初 は
ai2sとの対戦の通算成績の 勝率が向上する が、深さの上限が 5 を超えたあたり から 勝率が下がる - 敗率 は 深さの上限が増える と 減り、深さの上限が 5 以上になると 0 % になる
- 従って、深さの上限が 5 以上 の場合は 弱解決の AI である
深さの上限が 5 の場合に 弱解決の AI である ことは、下記のプログラムで確認できます。
from util import Check_solved
Check_solved.is_weakly_solved(ai_abs_dls, params={"eval_func": ai10s, "maxdepth": 5,
"eval_params": {"minimax": True}})
実行結果
o True
x True
Both True
残念ながら深さの上限が 5 の場合は、下記のプログラムの実行結果から 100 % と表示されないので強解決の AI ではありません。
Check_solved.is_strongly_solved(ai_abs_dls, params={"eval_func": ai10s, "maxdepth": 5,
"eval_params": {"minimax": True}})
実行結果
100%|██████████| 431/431 [00:03<00:00, 121.83it/s]
422/431 97.91%
また、グラフから以下の事がわかります。
-
ai14sの勝率 も同様に 深さの上限が 5 以上 になると 下がる -
深さの上限を上げる と
ai5s、ai10s、ai14sの 通算成績は近づいていき、深さの上限が 8 になると ほぼ同じ になる
このようなことが起きる原因は、深さの上限が 8 の場合に 行われる処理 を考察することで理解できます。深さの上限を 8 とした場合は、静的評価関数が 評価値が計算するノード は すべてゲームの決着がついた局面 になります。別の言葉で言い換えると、深さの上限 を ゲーム木の深さ以上に設定 した深さ制限探索は、深さの制限を行わない ゲーム木の 探索と同じ処理 を行うということです。ai5s、ai10s、ai14s はいずれも 決着がついた局面の評価値を正しく計算できる ので、深さの上限を 8 以上 とした場合は 強解決の AI になります。
下記は静的評価関数を ai5s、深さの上限を 8 とした場合 ai_abs_dls が強解決の AI であることを確認するプログラムです。
Check_solved.is_strongly_solved(ai_abs_dls, params={"eval_func": ai5s, "maxdepth": 8,
"eval_params": {"minimax": True}})
実行結果
100%|██████████| 431/431 [00:03<00:00, 121.48it/s]
431/431 100.00%
また、ゲーム木の中には 浅い深さのノード で ゲームの決着がつく 場合があります。例えば (0, 0)、(1, 0)、(0, 1)、(1, 1)、(0, 2) の順で着手を行うと、深さが 5 のノードの局面で決着 がつきます。深さ制限探索で 深さの上限を上げる と近似値の 精度が上がる理由の一つ は、静的評価関数が計算するノードの中で、正確な評価値を計算できる ゲームの 決着がついた局面の割合が増える ため、静的評価関数が計算した 近似値の精度の平均値が高くなる ためです。
上記をまとめると下記のようになります。
静的評価関数 がゲームの 決着がついた局面の評価値を正確に計算できる場合 は、深さの上限 を ゲーム木の深さ以上に設定 した深さ制限探索を行うことで 正確な評価値を計算 することができるようになる。
また、深さの上限を増やすことで と静的評価関数が計算するゲームの 決着がついた局面の割合が増える場合 は、評価値の精度が高く なる。
ai2s と ai3s が深さの上限を増やしても 精度が上がらない理由 は、どちらも 決着がついた局面の評価値 を 正確に計算できないから です。
深さの上限を増やした場合に精度が上がる別の理由
深さの上限を増やした場合に 精度が上がる他の理由 には以下のようなものがあります。
一般的 に、多くのゲームでは ゲームが進行 するにつれて 勝敗の形勢がはっきりします。例えば 〇× ゲームでは ゲーム開始時の局面 ではすべてのマスが空であるため、ゲーム盤の局面だけから どちらが有利であるかの 形勢を判断することが困難 ですが、マスが埋まっていく につれて 形勢が急速にはっきり していきます。
深さの上限を増やす ということは、より多くゲームが進行した局面 に対して静的評価関数が 形勢を判断する ことになるので、より精度の高い評価値を計算 できるようになる 可能性が高くなります。特に多くのゲームでは 形勢がはっきりしやすい ゲームの 終盤でその傾向が高くなります。
ただし、下記の理由から必ずしも深さの上限を増やすことで 精度が上がるとは限りません。
- ゲームの決着 がつくまでに 長い手数が必要 になるゲームの場合は、数手程度の着手 を行っても 形勢の判断にほとんど影響がない ことが多い
- 着手を進める ことで 形勢の判断が逆にしにくくなる ような場合がある
そのため上記の理由は 〇× ゲームには強く当てはまりますが、オセロや将棋などの他の多くのゲームの序盤ではではそれほど強く当てはまりません。
深さの上限を増やした場合に ai14s の勝率が下がる理由
実行結果のグラフから、深さの上限を増やす と ai10s と ai14s を静的評価関数とした場合の 勝率が下がる という、上記の説明とは 矛盾したように見える 結果が得られますが、それには理由があります。その理由について少し考えてみて下さい。
深さの上限を 8 とした ai10s や ai14s を静的評価関数とした深さ制限探索は、常にゲームの決着がついた局面 を静的評価関数で計算します。そのため、ai5s、ai10s、ai14s などの ゲームの決着がついた局面 の評価値を 正確に計算する静的評価関数 を利用した場合は、深さの上限を 8 とした場合にいずれも 同じ着手を選択 します。また、その際に選択する着手は、深さの上限を制限しない ゲーム木の探索で着手を選択する ai_gt6 と同じ になります。従って、その通算成績は下記の表のように以前の記事で計算した下記の ai_gt1 VS ai2s と ほぼ同じ になります。
| 関数名 | o 勝 | o 負 | o 分 | x 勝 | x 負 | x 分 | 勝 | 負 | 分 |
|---|---|---|---|---|---|---|---|---|---|
深さの上限 8 の ai5s |
96.8 | 0.0 | 3.2 | 76.8 | 0.0 | 23.2 | 86.8 | 0.0 | 13.2 |
ai_gt1 |
96.9 | 0.0 | 3.1 | 78.0 | 0.0 | 22.1 | 87.4 | 0.0 | 12.6 |
ai14s VS ai2s の通算成績が ai_gt1 VS ai2s よりも良い理由 は、ai14s がゲームの 決着がついていない局面 の 性質を考慮した評価値を計算 して着手を選択することで、最善手の中 で ai2s と対戦 した場合に 勝ちに結びつきやすい 合法手が選択されるからです。深さの上限を 8 とした場合は、ゲームの 決着がついている局面 の評価値しか 計算されなくなり、すべての最善手 の中から ランダムに着手を選択 するようになるので、ai2s に対する勝率は低くなってしまいます。
一般的なゲームにおける深さの上限と精度の関係
〇× ゲーム はゲーム木の深さが 9 と浅く、ノードの数もそれほど多くない ので今回の記事で説明した理由で、深さの上限を増やす と深さ制限探索の 精度が向上 します。
しかし、オセロや将棋など のゲーム木は 深さがかなり深く、ノードの数が多すぎる ので、 ほとんどの局面 で深さ制限探索で すべてのノードを探索できる ほど深さの上限を 増やすことはできません。そのため、特に 序盤の局面 では 今回の記事で説明した理由 では深さの上限を増やしても 精度は上がりません。それにも関わらず深さの上限を増やすと 一般的に精度が上昇する のは 別の理由があるから です。その理由については次回の記事で説明しますが、簡単に言うと 深さの上限を深くする ことで より多くの局面の評価値を計算 し、その中から 総合的に最善手を選択することができる ことが理由です。別の言葉で説明すると、より広い視野 で最善手を選択することができるということです。
なお、オセロや将棋のようなゲームであっても、ゲームの 決着が間近の局面 をルートノードとする 部分木 は 深さが浅くノードの数が少ない ため 深さの上限を部分木の深さ以上 にして 計算を行うことができる 可能性が高くなります。そのような場合 は、ゲームの決着がついた局面の評価値を正確に計算できる静的評価関数であれば、今回の記事で説明した理由から深さの上限を増やすことで 正確な最善手を計算できる ようになります。
人間のゲームでの思考と深さ制限探索
深さ制限探索 は、人間がゲームを遊ぶ際の思考 と よく似ています。
ゲームの 初心者 は、現在の局面の合法手 の中からいくつかを 着手した局面を思い浮かべ、その中から 最も良さそうだと考えた合法手を着手 します。このような 1 手先の局面だけ から着手を選択する方法は、深さの上限を 1 とした 深さ制限探索と同じ です。また、初心者 は局面の 形勢判断を正しく行うことができない ので、その思考は 精度の低い静的評価関数 であるとみなすことができます。
ゲームの 上級者 は、現在の局面から 数手先までの局面を思い浮かべ、その中から 最も自分にとって 有利な局面になると考えた合法手を着手 します。このような 数手先の局面 から着手を選択する方法は、深さの上限を 2 以上 とした 深さ制限探索と同じ です。将棋のプロは場合によっては 10 手以上先の局面まで考えながら着手を行うそうで、その場合は深さの上限を 10 以上とした深さ制限探索を行っています。またゲームの 上級者 は局面の 形勢判断うまく行うことができる ので、精度の高い静的評価関数 であるとみなすことができます。
初心者 が何手も 先の局面を読むことができない理由 の一つに、局面の 形勢判断に時間がかかる ということが挙げられると思います。それに対し、ゲームの 上級者 は局面の 形勢判断を短い時間 で行うことができるので、同じ時間 でも初心者よりも より深い探索を行う ことができます。
上記から、ゲームの 上級者が強い理由 は以下の点にあることがわかります。
- 局面の 形勢判断 を 短い時間 で 高い精度 で行うことができる
- 何手も先 の局面までを 考慮して着手を選択 する
これを 深さ制限探索 にあてはめると下記のようになります。
- 静的評価関数 が 短い時間 で 精度の高い 近似値を計算できる
- 大きな深さの上限 で深さ制限探索を行う
人間がゲームを遊ぶ際の思考と、ゲーム木の探索には違う点もありますが、上記から 強い AI を作成 する際に、下記の点が重要 であると言えるでしょう。
- 静的評価関数 の 精度が高い こと
- 静的評価関数の 計算時間が短い こと
- 深さ制限探索の 深さの上限が多く、多くの局面の評価値を計算 できる こと
なお、深さの上限 や 計算する局面の数を増やす ために必要となるのは、静的評価関数の計算時間だけでなく、αβ 法などの 効率の良い探索アルゴリズムを利用 することも重要です。
今回の記事のまとめ
今回の記事では、ゲーム木に対する 深さ制限探索 が一般的に下記のような性質を持つことを説明しました。
- 深さの上限を上げる と 処理時間 が 指数関数的に増える
- 深さの上限を上げると 評価値の精度が高くなる。ただし、静的評価関数 が最低でも 決着がついた局面 の評価値を 正確に計算できる 必要がある
- 深さの上限 を ゲーム木の深さよりも多くする と 深さを制限しないゲーム木の探索 になるので、計算される評価値の 精度が 100 % になり、強解決の AI を作成 できる
また、今回の記事で検証から 深さの上限を上げる と 精度が高くなる理由 には以下のようなものがあることを示しました。
- 深さの上限を上げると、正確な評価値を計算できる 決着がついた局面 を静的評価関数が 計算する割合が増える ため
- 深さの上限を上げると、より多くの着手が行われた局面 に対して静的評価関数が評価値を計算することになる。一般的 に 着手が行われるほど形勢を判断しやすくなる ので 評価値の精度が上がる
今回の記事中でも説明しましたが、上記の 2 種類の理由は、決着がつくまでの手数が多い ゲームの 序盤の局面 では ほとんど効果はありません。例えば オセロ はゲームの 決着がつくまで ほとんどの場合で 60 回3の着手 を行う必要があります。そのため、オセロの 序盤の局面 では深さ制限探索で静的評価関数が 決着がついた局面 の評価値を 計算することは現実的に不可能 です。また、オセロは 1 回の着手 で多くのコマがひっくり返ることで ゲーム盤の状況が大きく変わることが多い ため、序盤の局面 では着手を複数回行っても 形勢を判断しやすくなるとは限りません。
次回の記事では、深さ上限を増やすと評価値の精度が高くなる別の理由を説明します。
本記事で入力したプログラム
| リンク | 説明 |
|---|---|
| marubatsu.ipynb | 本記事で入力して実行した JupyterLab のファイル |
| ai.py | 本記事で更新した ai_new.py |
次回の記事
-
前回の記事で説明したように、
ai_abs_dlsで 着手を選択 する際の 仮引数maxdepthは、ルートノードの 子ノードに対する 深さの制限探索の 深さの上限 を表すので、〇× ゲームのゲーム開始時の局面に対する深さの上限の 最大値 は 9 ではなく 8 です ↩ -
真ん中のマスに優先的に着手を行う AI と対戦する場合は、最初の手番で (1, 1) のマスが開いていればそこに着手を行うので、(1, 1) に着手を行うことで決着がつくことはありません。そのためこの性質は、対戦相手がランダムな着手を行う AI である必要があります ↩
-
どちらの手番もコマを置くことができないマスしかなくなった場合は 60 未満の手数で決着がつく場合があります ↩