Pythonで〇×ゲームのAIを一から作成する その55 必要条件と十分条件と、複数の条件を考慮した評価値

目次と前回の記事

これまでに作成したモジュール

以下のリンクから、これまでに作成したモジュールを見ることができます。

これまでに作成した AI

これまでに作成した AI の アルゴリズム は以下の通りです。

ルール	アルゴリズム
ルール1	左上から順 に 空いているマス を探し、最初に見つかったマス に 着手 する
ルール2	ランダム なマスに 着手 する
ルール3	真ん中 のマスに 優先的 に 着手 する 既に 埋まっていた場合 は ランダム なマスに 着手 する
ルール4	真ん中、隅 のマスの 順 で 優先的 に 着手 する 既に 埋まっていた場合 は ランダム なマスに 着手 する
ルール5	勝てる場合 に 勝つ そうでない場合は ランダム なマスに 着手 する
ルール6	勝てる場合 に 勝つ そうでない場合は 相手の勝利 を 阻止 する そうでない場合は ランダム なマスに 着手 する
ルール6改	勝てる場合 に 勝つ そうでない場合は 相手 が 勝利できる 着手を 行わない そうでない場合は ランダム なマスに 着手 する
ルール7	真ん中 のマスに 優先的 に 着手 する そうでない場合は 勝てる場合 に 勝つ そうでない場合は 相手の勝利 を 阻止 する そうでない場合は ランダム なマスに 着手 する
ルール7改	真ん中 のマスに 優先的 に 着手 する そうでない場合は 勝てる場合 に 勝つ そうでない場合は 相手 が 勝利できる 着手を 行わない そうでない場合は ランダム なマスに 着手 する
ルール8	真ん中 のマスに 優先的 に 着手 する そうでない場合は 勝てる場合 に 勝つ そうでない場合は 相手 が 勝利できる 着手を 行わない そうでない場合は、次 の 自分の手番 で 勝利できる ように、「自 2 敵 0 空 1」が 1 つ以上 存在する 局面になる着手を行う そうでない場合は ランダム なマスに 着手 する

基準となる ai2 との 対戦結果（単位は %）は以下の通りです。太字 は ai2 VS ai2 よりも 成績が良い 数値を表します。欠陥 の列は、アルゴリズム に 欠陥 があるため、ai2 との 対戦成績 が 良くても強い とは 限らない ことを表します。欠陥の詳細については、関数名のリンク先の説明を見て下さい。

関数名	o 勝	o 負	o 分	x 勝	x 負	x 分	勝	負	分	欠陥
ai1 ai1s	78.1	17.5	4.4	44.7	51.6	3.8	61.4	34.5	4.1	あり
ai2 ai2s	58.7	28.8	12.6	29.1	58.6	12.3	43.9	43.7	12.5
ai3 ai3s	69.3	19.2	11.5	38.9	47.6	13.5	54.1	33.4	12.5
ai4 ai4s	83.0	9.5	7.4	57.2	33.0	9.7	70.1	21.3	8.6	あり
ai5 ai5s	81.2	12.3	6.5	51.8	39.8	8.4	66.5	26.0	7.4
ai6	88.9	2.2	8.9	70.3	6.2	23.5	79.6	4.2	16.2
ai6s	88.6	1.9	9.5	69.4	9.1	21.5	79.0	5.5	15.5
ai7 ai7s	95.8	0.2	4.0	82.3	2.4	15.3	89.0	1.3	9.7
ai8s	98.2	0.1	1.6	89.4	2.5	8.1	93.8	1.3	4.9

用語の定義

これまでの記事で行ってきたいくつかの表記は、長く分かりづらいので、今回の記事から、下記の表記を行うことにします。

表記	これまでの記事での表記
ライン	直線（line）上に 並んだ 3 マス
「自 x 敵 y 空 z」が存在する着手	自分の手番 で 着手 を行った 結果、「自 x 敵 y 空 z」が 1 つ以上 存在する 局面になる着手

必要条件と十分条件

これまでの記事では、強い AI を作るために、さまざまな条件 を考えてきましたが、それらの 条件 は、必要条件、十分条件、その どちらでもない条件 に 分類 されます。この 分類 は、条件 によって AI が 強くなるかどうか に大きく関わる 重要な概念 なので、今回の記事では、最初にこの 分類 について、ルール 8 の 条件 を元に 説明 します。

ルール 8 の条件

ルール 8 には、さまざまな条件 がありますが、最後の「ランダムなマスに着手する」という 条件 は、強い AI を作るための 条件ではない ので、それを 削除 した、下記の条件 について 考える ことにします。以後の説明では、それぞれの条件を、条件 1 のように 番号 を使って 表記 することにします。

1. 真ん中 のマスに 優先的 に 着手 する
2. そうでない場合は 勝てる場合 に 勝つ
3. そうでない場合は 相手 が 勝利できる 着手を 行わない
4. そうでない場合は、次 の 自分の手番 で 勝利できる ように、「自 2 敵 0 空 1」が存在する着手 を行う

十分条件

ある 目的を達成 するために、その 条件 を 満たしていれば 必ず 目的を達成できる ような 条件 のことを、十分条件 と呼びます。ルール 8 の条件の中で、「勝てる場合 に 勝つ」という 条件 2 は、必ず勝利できる ので、強いAI の 目的を達成できる、十分条件 です。

十分条件 を 満たす ことで、必ず 目的を達成 することが できる ので、ルール に 十分条件 を 組み込む ことで、多くの場合 で AI を 強くする ことが できます。また、どんな場合 でも AI が 弱くなること は ありません。

ピンとこない人がいると思いますので、そのようなことが起きる 理由 について説明します。〇× ゲームの ある局面 が、下記の条件 を 満たす 場合の事を考えてみて下さい。

• 3 つの合法手 A、B、C が 存在 する
• 合法手 A が 〇×ゲームに勝つための 十分条件 を 満たし、残り の B と C は 満たさない

この 十分条件 を ルール に 組み込んだ AI と そうでない AI が 選択 する 着手 と、その 結果 は 以下の表 のようになります。

	着手	結果
組み込んだ AI	A	必ず勝利 する
組み込んでいない AI	A、B、C	A を選んだ場合 は 必ず勝利 する B、C を選んだ場合 はどうなるか わからない

表からわかるように、この 十分条件 を 組み込んだ AI のほうが、組み込んでいない AI よりも 勝率が悪くなる ことは 決してありません。また、上記では、合法手の数を 3 つとしましたが、合法手の数 が いくつであっても同様 です。

なお、以下 の 条件 が満たされる場合は、AI の強さ は 変わりません。

• A 以外 を 選択 した 後の局面 に対して、ルールを適用 した 結果、必ず勝利 する場合
• ルールの 他の条件 によって、A 以外 が 選択されない 場合
• A 以外 の 合法手 が 存在しない 場合

上記の説明は、以前の記事での ルール 5 の 検証 と 同様 ですが、今回はルール 5 だけでなく、十分条件 を 満たす場合 に 一般化 しています。

十分条件 を ルールに組み込むこ とで、AI が 強くならない場合 があるが、弱くなる ことは 決してない ので、十分条件 であることが 分かっていれば、 安心して ルールに 組み込む ことが できる。

一般的 に、十分条件 は、目的 を 達成する ための 条件の一部 でしかありません。そのことは、条件 2 のみ を ルール とする、ルール5 によって作られた ai5 より も 強い AI を、実際に 作成できている ことから 明らか でしょう。

必要条件

ある 目的を達成 するために、必要 となる 条件 のことを 必要条件 と呼びます。ルール 8 の、「相手 が 勝利できる 着手を 行わない」という 条件 3 は、この 条件を満たす着手 を 行わない と、次の相手の手番で 相手が勝利してしまう 可能性があるので、必要条件 です。

必要条件 は、目的の達成 を 保証 するものでは ありません が、少なくとも その条件 を 満たさなければ、目的を達成 することは 不可能 なので、AI のルールに 必要条件 を 加える ことで、AI が 強くなること が 期待できます。また、AI が 弱くなる ことは ありません。

ピンとこない人がいると思いますので、そのようなことが起きる 理由 について説明します。〇× ゲームの ある局面 が、下記の条件 を 満たす 場合の事を考えてみて下さい。

• 3 つの合法手 A、B、C が 存在 する
• 合法手 A が 〇×ゲームに勝つための 必要条件 を 満たし、残り の B と C は 満たさない

この 必要条件 を ルール に 組み込んだ AI と そうでない AI が 選択 する 着手 と、その 結果 は 以下の表 のようになります。

	着手	結果
組み込んだ AI	A	どうなるかは わからない
組み込んでいない AI	A、B、C	A を選んだ場合 はどうなるかは わからない B、C を選んだ場合 は、勝利 することは ない

表から、組み込んでいない AI は 絶対 に 勝利できない B と C を 選択する可能性 がありますが、組み込んだ AI は、それらを 選択 することは ありません。そのため、組み込んだ AI のほうが、組み込んでいない AI よりも 勝率が悪くなる ことは 決してありません。また、上記では、合法手の数を 3 つとしましたが、合法手の数 が いくつであっても同様 です。

なお、以下 の 条件 が満たされる場合は、AI の強さ は 変わりません。

• A を 選択 した 後の局面 に対して、ルールを適用 した 結果、必ず勝利できない 場合
• ルールの 他の条件 によって、A 以外 が 選択されない 場合
• A 以外 の 合法手 が 存在しない 場合

必要条件 を ルールに組み込むこ とで、AI が 強くならない場合 があるが、弱くなる ことは 決してない ので、必要条件 であることが 分かっていれば、 安心して ルールに 組み込む ことが できる。

十分条件 と 必要条件 で、上記のように 同じ結論 が得られましたが、それぞれの 結論がでる理由 は以下のように 異なります。

• 十分条件 は、目的 を 達成する選択 を 行う ことで、AI を強くできる
• 必要条件 は、目的 を 達成しない選択 を 行わない ことで、AI を強くできる

なお、あまりにも 緩い必要条件 を 満たしても、目的の達成 には ほとんど寄与しない 点に 注意 して下さい。例えば、テストで 100 点を取る という 目的 に対する 必要条件 として、テストを受ける という 条件 が考えられます。テストを受けなければ 絶対に 100 点を取れない ので、この条件 はれっきとした 必要条件 ですが、よほど簡単なテストでない限り、テストを受けるだけ で 100 点をとる ことができることは まずない でしょう。

必要条件 と 十分条件 を ルールに加える ことで、AI を 強くできる根拠 を示しましたが、必要条件 と 十分条件 を むやみに加えても、AI が思ったように 強くならない ことが良くあります。次は、どのような 必要条件と十分条件を 考えればよいか について 説明 します。

必要十分条件

必要条件 と 十分条件 の 両方を満たす ような 条件 のことを 必要十分条件 と呼び、以下 のような 性質 を持ちます。

• 目的 を 達成できない条件 は 含まれない
• 目的 を 達成できる条件 を すべて含む

必要十分条件 の数は 一つ ですが、必要条件 や 十分条件 を満たす条件は 複数 あります。

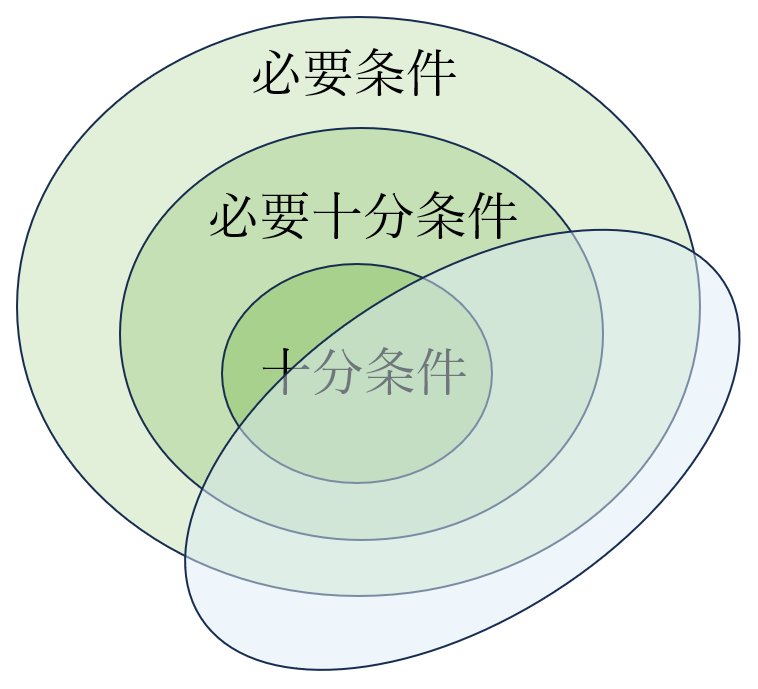
必要条件、十分条件、必要十分条件 の 関係 を図で書くと、下図 のようになります。

それぞれの条件 を、以前の記事で説明した、集合 として考えると、それぞれの条件は、下記のような 包含関係 にあります。これらのことから、必要条件、必要十分条件、十分条件 の 順 で、条件が厳しくなる ことがわかります。

$必要条件 ⊃ 必要十分条件 ⊃ 十分条件$

必要十分条件 を 知る ことで、その条件 に 従うこと が できれば¹、必ず目的を達成 することが できます。しかし、実際 には、必要条件 や 十分条件 が わかっても、必要十分条件 が何であるかがはっきりと わからない ことが 良くあります。実際に、〇×ゲーム の 強い AI を作成 するための 必要条件 と 十分条件 は既に いくつか示しました が、必要十分条件 を考えることは 簡単 なこと ではありません。

わかりやすいように、〇×ゲーム以外の 具体例 を挙げて説明します。「漢字のテストで良い点数をとる」という 目的 に対する 必要条件 ははっきりとは 分かりません が、必要条件 や 十分条件 であれば、下記のように 簡単に考える ことが できます。

• 必要条件 の 一つ は「漢字の勉強をする」である
• 十分条件 の 一つ は「国語辞典の漢字をすべて暗記する」である

ただし、上記のような 簡単すぎる必要条件 は目的を達成の 役に立ちません し、厳しすぎる十分条件 は 実行することが困難 という意味であまり 役に立ちません。

必要十分条件 が 分からない場合 は、できるだけ厳しい 条件の 必要条件 と、できるだけ緩い 条件の 十分条件 を考え、2 つ の 中間の性質 を持つ、必要十分条件 に 近い条件 で 目的の達成 を 試みる ことになります。例えば、上記の例の場合は より厳しい必要条件 と、より緩い十分条件 として下記のような条件を考え、その 中間の条件 で勉強を行います。

• 必要条件 に 勉強時間 を 指定 した「漢字の勉強を 1 日 30 分勉強する」を考える
• 漢字のテストには 漢字の意味 は 必要ない ので、十分条件 を 緩めた「国語辞典の漢字の読み方だけをすべて暗記する」を考える

下図左 は 元の条件 を、下図右 は 新しい条件 を 図で表した ものです。実際に採用 するのは 色のついている部分 の いずれかの条件 で、新しい条件 を考えることで、色のついている部分 の 面積が減る ので、採用する条件 が 必要十分条件 に より近く なる 可能性が高くなる ことが分かります。

必要十分条件 が わからない場合 は、必要十分条件 に 近くなる ように、できるだけ厳しい必要条件 と、できるだけ緩い十分条件 を考え、その 中間の性質 をもつ 条件 を 利用 することで、目的の達成 を 試みる という方法がある。

上記で できるだけ厳しい必要条件 と述べましたが、厳しくしすぎる と 必要条件 では なくなって しまいます。また、厳しさの限界 を 見つける のは 簡単 なことでは ありません。例えば、漢字のテスト の例の場合は、一日に 勉強する時間 を 増やす ことで、条件を厳しく することは できます が、例えば 「漢字の勉強を 1 日 10 時間勉強する」のように、厳しくしすぎて しまうと、必要条件 では なくなってしまう からです。これは、十分条件 の場合も 同様 で、緩くしすぎる と 十分条件 では なくなってしまいます。

これは あたりまえ のことで、必要条件 の 厳しさの限界 が、必要十分条件 であり、そもその 必要十分条件 が何であるかが わからないこと に 困っている からです。

複数の必要条件、十分条件

上記の説明を聞くと、必要条件 と 十分条件 は、最も厳しい（緩い）ものを 1 つだけ考えればよい と思う人がいるかもしれませんが、そうではありません。異なる 必要条件や十分条件が 包含関係にない 場合は、複数 の 必要条件 や 十分条件 を 考える価値 が あります。

下図は、包含関係にない、必要条件 1 と 必要条件 2 を表したものです。この 2 つの十分条件 の 両方を満たす ような 条件 の 水色の面積 は、元の 必要条件 1 と 必要条件 2 の それぞれの面積 よりも 小さくなっている ので、条件が厳しくなる ことが分かります。

下図は、包含関係にない、十分条件 1 と 十分条件 2 を表したものです。この 2 つの十分条件 の いずれかを満たす ような 条件の面積 は、元の 十分条件 1 と 十分条件 2 の それぞれの面積 よりも 大きくなっている ので、条件が緩くなる ことが分かります。

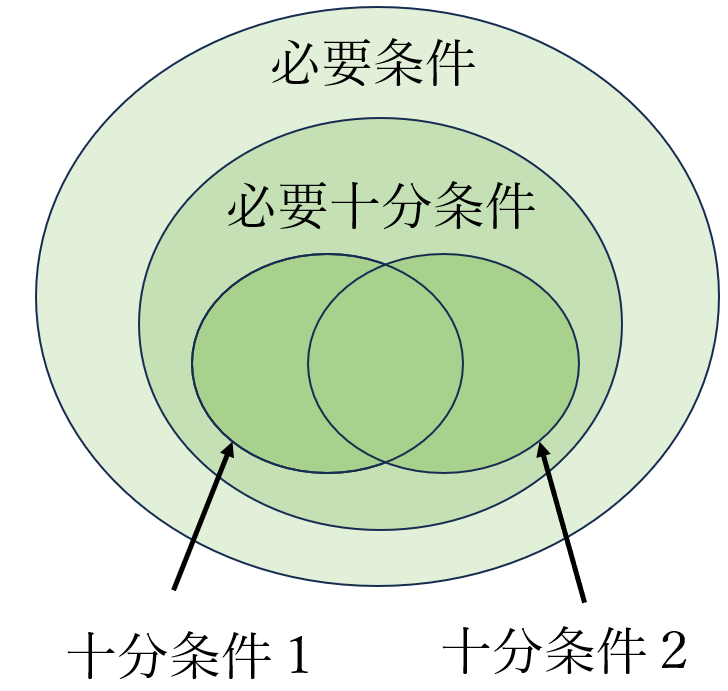
逆に言えば、包含関係 にある 複数 の 必要条件 や 十分条件 は、そのうちの 最も厳しい（緩い）条件以外 は 必要ありません。

条件 3 が必要条件ではないことの説明

以前の記事で、〇×ゲームに勝つ方法 について 考察 し、 勝つため の 条件 として、「自 2 敵 0 空 1」が 存在する着手 を行う 必要がある という 考察 を行いました。このことから、直観的 に、ルール 8 の『「自 2 敵 0 空 1」が 存在する着手 を 行う』という 条件 4 は 必要条件 であるように 思えるかもしれません が、実際 には 必要条件ではありません。

確かに、〇×ゲーム に 勝つため には、ゲームが開始してから終了するまでの間の いずれかの局面 で、「自 2 敵 0 空 1」が 存在する着手 を 行う必要がある ことは 間違いありません が、それを いつ行うべきか についての 考察 は、以前の記事では 行っていません。そのため、ある局面 で「自 2 敵 0 空 1」が 存在する着手 を 行うことができたとしても、その着手を すぐに行う ことが勝利するために 必要である とは 限りません。

条件 4 は以前に考察した 必要条件 と 異なり、「自 2 敵 0 空 1」が 存在する着手 を 行うことができる 場合に、すぐに着手を行う という 条件 なので、必要条件 ではありません。

そのような細かい違いはどうでも良いのではないかと思う人がいるかもしれませんが、細かい違いであっても、目的の達成 に 大きな影響を及ぼす可能性 があるので 重要 です。

別の言葉 で 説明 すると、目的を達成 するために、必ず行わなければならない ことであったとしても、すぐに行わず に、後回し にしたほうが 良い場合がある ということです。もちろん、逆に 後回し に してはいけない場合 も あります。

ピンとこない人が多い と思いますので、いくつかの 具体例で説明 します。本当は ゲームの例だけで説明をしたかったのですが、大富豪やオセロなどのゲームに詳しくない人には意味が分からない説明になるので、最初の例 は ゲームとは関係のない例 で説明します。

カップ麺を食べる 際に、お湯を注いで蓋をした後に、必ず 食べる前に 蓋を開ける必要 があります。つまり、蓋を開ける ことが、カップ麺を食べる ための 必要条件 です。しかし、蓋を開ける必要がある からといって、お湯を注いだ直後 に 蓋を開けた場合 は おいしいカップ麺 が 食べられません。この場合は、3 分待ってから 蓋を 開けるべき です。

大富豪 というトランプの ゲームの目的 は、自分 の手持ちの カードをすべて捨てる ことなので、カードを捨てる ことが勝つための 必要条件 になります。しかし、強いカード をゲームの 早いうちに捨ててしまう と、ゲームの終盤に弱いカードしか手元に残らなくなってしまうため、ゲームに 勝つこと が 困難になります。

オセロ というゲームは、ゲーム終了時に 自分の色の駒の数 が 多いほうが勝利 します。そのため 初心者 は、ゲームの 序盤 から 自分の色 の 駒の数が多くなる ような 着手 を 行う人が多い ようですが、実際には 序盤 で そのような着手 を行うと、大きく不利 になる場合が多く、勝つこと が 困難になります。

必要条件でも十分条件でもない条件

ルール 8 の 条件 4 は、必要条件 では ありません が、どのタイミング で「自 2 敵 0 空 1」が 存在する着手 を 行えば良いよいか については、現時点での考察では はっきりとしていません。また、実際 に どのタイミング で「自 2 敵 0 空 1」が 存在する着手 を 行えば良いよいか を 考察 して 見つける ことは 簡単ではありません。興味がある方は少し考えてみて下さい。簡単に答えが出せない ことが 実感できる のではないかと思います。

そのような場合に、どこかで必ず「自 2 敵 0 空 1」が 存在する着手 を 行う必要がある のだから、必要条件ではない 条件 4 を 入れる価値がある と 判断 して 採用する という 考え方があり、実際 に そのような理由 で、必要条件 でも 十分条件 でも ない 条件を ルールに 組み込む ことが 良く行われます。

そのようなことが行われる 理由 は、目的を達成 するために 有効 な、必要条件 や 十分条件 を 満たす条件 を 数多く考える ことが、困難な場合が多い からです。また、思いついた場合 でも、本当に その条件 が 必要条件 や 十分条件 であるかどうかの 証明を行う ことが 難しい場合 が 良くあります。なお、上記で 有効な という条件をつけたのは、先程の例で挙げた「テストの勉強をする」、「辞書を暗記する」のような、ほとんど 意味のない、緩い必要条件 や、厳しい十分条件 であれば、いくらでも考えることができる からです。

一方、必要条件 や 十分条件 であることは 証明できない が、有効そうである 条件であれば、証明を行う必要がない ので、気軽に考える ことが できます。実際 に ルール 8 の「真ん中のマス に 優先的に着手 する」という 条件 1 は、必要条件 であることは 証明されていません が、有効 である 可能性が高い ことを以前の記事で 考察 し、実際 に ルール 3 に 組み込んだ結果、強くなる ことが 確認できました。

必要条件 でも 十分条件 でも ない 条件は、ルールに組み込む ことによって 弱くなる可能性 があります。そのため、その条件が 有効であるか どうかはどうかは、その 条件 を ルール に 組み込んでいない 他の AI と対戦 して 比較する ことで 確認する 必要があります。比較した結果、強く なっていれば 採用 し、弱く なっていれば 採用を見送り ます。

下図の 薄い水色 が、必要条件 でも 十分条件 でも ない条件 の 例 です。図からわかるように、必要条件の外 に はみ出している部分 があり、その部分 によって 選択が行われる と、目的が達成できなく なります。また、必要十分条件 に 重なっている部分 によって 選択が行われる と、目的が達成 できます。従って、必要条件 や 十分条件 を 考える場合 と 同様 に、必要十分条件 に 近くなるような条件 を 考える ことが 重要 になります。

以前の記事でも言及しましたが、ルールベースの AI は、必要条件 でも 十分条件 でもない 条件を追加 することで、下記 のような 問題が発生 することが 多い ため、ルールベースで 強い AI を 作る のはかなり 困難な作業 になります。

• 以前の記事の ルール 4 で 追加 した「真ん中、隅 のマスの 順 で 優先的 に 着手 する」という 条件 のように、一見 すると AI が 強く なっている ように見える が、実際 には 特定 の AI に 対してのみ強く なっているという 場合 がある
• 条件が増える と、条件どうし の 相性 や 矛盾 などの 問題 で、突然 AI が弱くなる という 現象が発生 することがある
• 条件が増える と、ルール が 複雑になりすぎて、何を行っているか が 分かりづらくなる²
• 条件が増える と、新しい 有効な 条件を考える ことが 困難 になる
• 条件が増える と、新しい条件 を 追加 してもほとんど AI が 強くならなく なる

従って、最近 の AI は 人間 が ルールを考える というルールベースではなく、AI が 自動的 に ルール を 発見 する、機械学習 という手法を使ったものが 主流 になっています。〇×ゲームの AI を機械学習で作成する方法については、今後の記事で紹介します。

なお、〇×ゲーム は、単純 なゲームなので、ルールベース でも 最強の AI を作る ことが 可能 なので、引き続きルールベースで 〇×ゲームの AI を作成します。

ルールベースの AI の作成手順

ルールベースの AI の 一般的 な 作成手順 をまとめます。本記事 でも、実際 に 下記の手順 でこれまで 〇×ゲーム の AI を作成 してきました。

• 必要十分条件 を 考える ことが できれば、それを ルールに組み込む ことで 最強の AI を 作成できる が、一般的 には 必要十分条件 が 分からない ことが 多い
• 十分条件 を考え、ルール に 組み込む ことで、AI を 強くする
• 必要条件 を考え、ルール に 組み込む ことで、AI を 強くする
• 必要条件 でも 十分条件 でも ない、有望そうな条件 を考え、ルール に 組み込んで AI を 実装 し、他の AI と 対戦する ことでその 性能を確かめる
  • 強くなっていれば その 条件を採用 する
  • 強くならない（弱くなっている）場合は、その 条件 を 破棄 する³

2 つ目の十分条件を組み込んだ AI

ルール 8 の 条件 2 は、現在の局面 で 勝利できる場合 に 勝利する というものでしたが、未来の局面 で 必ず勝利できる場合 でも 強い AI の 目的を達成 することが できます。そこで、次 の 自分の手番 の 局面 で 必ず勝利できる ための 条件 を 考える ことができれば、それを 十分条件 と みなす ことが できます。〇×ゲームにある程度慣れている方には当たり前の事かもしれませんが、それがどのような条件であるかについて少し考えてみて下さい。

まず、前提条件 を 明確 にすることにします。次 の 自分の手番 で 勝利できる ということから、「現在の局面 で 勝利できない」という 条件が必要 です。また、次 の 相手の手番 で 相手が勝利 すると 目的 が 達成できない ので、「次 の 相手の手番 で 相手 が 勝利しない」という 条件が必要 になります。これらは、ルール 8 の 条件 2 と 3 によって 判定できます。

ルール 8 の 条件 4 の 着手 を行っても、必ず勝利 できるとは 限らない理由 は、〇×ゲーム は、自分と相手 が 交互 に 着手を行う ゲームなので、「自 2 敵 0 空 1」が 存在する着手 を行っても、次 の 相手の手番 で「自 2 敵 0 空 1」の ライン の 空いているマス に 相手 が 着手を行う ことで、邪魔 をされてしまう 可能性がある からです。

しかし、「自 2 敵 0 空 1」の ライン が 2 つ以上 ある場合は、次 の 相手の手番 で 邪魔をできる のは、そのうちの 1 つ の ラインだけ です。例えば、下図 の局面の場合、× が 次 の 〇 の手番 での 勝利を阻止 するためには、2 つ ある 黄色のマス に 着手 を 行う必要 がありますが、自分の手番 で行える 着手 は 1 マスだけ なので、どちらか の 黄色のマス は必ず 空のまま 残ってしまうので、次 の 〇 の手番 で 〇 が 必ず勝利 することが できます。

従って、次 の 自分の手番 の局面で 必ず勝利できる ための 条件 は、以下 のようになることが分かります。

• ルール 8 の 条件 2 を 満たさない
• ルール 8 の 条件 3 を 満たさない
• 「自 2 敵 0 空 1」が 2 つ以上 存在する 着手 を行う

同様に、2 手先 や 3 手先 の 自分の手番 で自分が 必ず勝利できる条件 を考え、それを 十分条件 と みなす ことが できます が、でそのような 条件 を みつける のは 簡単ではありません。数手先 の 未来の局面 を 本格的 に 考慮に入れる AI については、ルールベースの次の、探索型の AI の所で 説明 します。

ルール 9 の定義

上記の条件 を ルール 8 に 加えた、ルール 9 を下記のように 定義 する事にします。新しい条件 は、十分条件 なので、十分条件でない ルール 8 の 条件 4 よりも 優先順位 を 高くする 必要があります。下記が ルール 9 の 定義_ です。なお、新しい条件 の 内容 に 合わせて、ルール 8 の 条件 4 を、『「自 2 敵 0 空 1」が 存在する着手 を行う』から『「自 2 敵 0 空 1」が 1 つ存在 する 着手 を行う』のように修正しました。

今回から、それぞれの 条件の種類 を 表で示す ようにしました。種類 の列が 空欄 になっている 条件 は、必要条件 でも、十分条件 でも ない ことを表します。また、条件 は 優先順位 の 高い順 に 並んでいる ので、「そうでない場合は」は 削除 しました。

条件	種類
真ん中 のマスに 優先的 に 着手 する
勝てる場合 に 勝つ	十分条件
相手 が 勝利できる 着手を 行わない	必要条件
次 の 自分の手番 で 必ず勝利できる ように、「自 2 敵 0 空 1」が 2 つ以上存在する着手 を行う	十分条件
次 の 自分の手番 で 勝利できる ように、「自 2 敵 0 空 1」が 1 つ存在する着手 を行う
ランダム なマスに 着手 する

ルール 9 の 評価値 をどのように 設定 すればよいかについて少し考えてみて下さい。

評価値の設定

下記は、ルール 8 の 評価値 の 設定 です。

優先順位	局面の状況	評価値
1	真ん中のマスに着手している	3
2	自分が勝利している	2
4	「自 2 敵 0 空 1」が 1 つ以上存在する	1
5	「自 2 敵 0 空 1」が存在しない	0
3	相手が勝利できる	-1

上記の表に、ルール 9 の『「自 2 敵 0 空 1」が 2 つ以上存在する』 という 新しい条件 を 追加 した状態の 評価値を設定 する必要があります。

下記の表は、ルール 9 の 条件の優先順位 に注意しながら 評価値 を 設定 した例です。上 2 つ の 評価値 は、新しい条件の追加に合わせて 修正 しました。

優先順位	局面の状況	評価値
1	真ん中のマスに着手している	4
2	自分が勝利している	3
4	「自 2 敵 0 空 1」が 2 つ以上存在する	2
5	「自 2 敵 0 空 1」が 1 つ存在する	1
6	「自 2 敵 0 空 1」が存在しない	0
3	相手が勝利できる	-1

マークのパターンを数える関数の定義

『「自 2 敵 0 空 1」が 2 つ以上存在する』 という 条件 を 判定 するためには、マークパターン の数を 数える 必要がありますが、enum_markpats は、マークのパターン が 存在するかどうか を計算するだけで、数を 数える機能 を 持たない ので、利用 することは できません。そこで、マークのパターン の数を 数える 下記の メソッド を 定義 する事にします。

• 名前：マーク（mark）の パターン（pattern）を 数える（count）ので、count_markpats という 名前 にする
• 処理：インスタンスの 局面 の マークのパターン を 数える
• 入力：なし
• 出力：マークのパターン を 数えた データを 返り値 として 返す

enum_markpats を 修正 し、マークのパターン を 数える機能 を 追加 するという方法も 考えられます が、名前 に 列挙（enumerate）の単語が入ったメソッドで、列挙 とは 異なる 数える（count）という 処理 を 行うようにする と、プログラムが わかりづらくなる ので、本記事では 別の名前 の メソッドを定義 する事にします。

数 を 数える処理 は、count_marks と同様に、以前の記事で紹介した、defaultdict を 利用 する方法が 考えられます。count_marks では、defaultdict の キー に マーク を表す 文字列 を 利用 しましたが、count_markpats では、マークのパターン を 数える 必要があるので、defaultdict が 使えない と 思う人 が いるかもしれません。実際 には、dict や defaultdict は、キー に ハッシュ可能なオブジェクト を 利用 でき、前回の記事で、マークのパターン を表すデータを ハッシュ可能なオブジェクト である NamedTuple に 変更 したので、マークのパターン を defaultdict を使って 数える ことが 可能 です。下記は、count_markpats の 定義 で、enum_markpats を 修正 することで、簡単に定義 することが できます。

なお、enum_markpats は削除せず、そのまま残しています。

• 5 行目：マークのパターン を 数える 変数を 初期化 する際に 代入する値 を、空の set から 空の defaultdict に 修正 する
• 10、12、15、18 行目：マークのパターン の キーの値 に 1 を足して 数を 数える

 1  from marubatsu import Marubatsu, Markpat
 2  from collections import defaultdict
 3
 4  def count_markpats(self):
 5      markpats = defaultdict(int)
 6 
 7      # 横方向と縦方向の判定
 8      for i in range(self.BOARD_SIZE):
 9          count = self.count_marks(coord=[0, i], dx=1, dy=0, datatype="tuple")
10          markpats[count] += 1
11          count = self.count_marks(coord=[i, 0], dx=0, dy=1, datatype="tuple")
12          markpats[count] += 1
13      # 左上から右下方向の判定
14      count = self.count_marks(coord=[0, 0], dx=1, dy=1, datatype="tuple")
15      markpats[count] += 1
16      # 右上から左下方向の判定
17      count = self.count_marks(coord=[2, 0], dx=-1, dy=1, datatype="tuple")
18      markpats[count] += 1
19
20      return markpats
21
22  Marubatsu.count_markpats = count_markpats

行番号のないプログラム

from marubatsu import Marubatsu, Markpat
from collections import defaultdict

def count_markpats(self):
    markpats = defaultdict(int)
 
    # 横方向と縦方向の判定
    for i in range(self.BOARD_SIZE):
        count = self.count_marks(coord=[0, i], dx=1, dy=0, datatype="tuple")
        markpats[count] += 1
        count = self.count_marks(coord=[i, 0], dx=0, dy=1, datatype="tuple")
        markpats[count] += 1
    # 左上から右下方向の判定
    count = self.count_marks(coord=[0, 0], dx=1, dy=1, datatype="tuple")
    markpats[count] += 1
    # 右上から左下方向の判定
    count = self.count_marks(coord=[2, 0], dx=-1, dy=1, datatype="tuple")
    markpats[count] += 1

    return markpats

Marubatsu.count_markpats = count_markpats

修正箇所

from marubatsu import Marubatsu, Markpat
from collections import defaultdict

-def enum_markpats(self):
+def count_markpats(self):
-   markpats = set()
+   markpats = defaultdict(int)
 
    # 横方向と縦方向の判定
    for i in range(self.BOARD_SIZE):
        count = self.count_marks(coord=[0, i], dx=1, dy=0, datatype="tuple")
-       markpats.add(count)
+       markpats[count] += 1
        count = self.count_marks(coord=[i, 0], dx=0, dy=1, datatype="tuple")
-       markpats.add(count)
+       markpats[count] += 1
    # 左上から右下方向の判定
    count = self.count_marks(coord=[0, 0], dx=1, dy=1, datatype="tuple")
-   markpats.add(count)
+   markpats[count] += 1
    # 右上から左下方向の判定
    count = self.count_marks(coord=[2, 0], dx=-1, dy=1, datatype="tuple")
-   markpats.add(count)
+   markpats[count] += 1

    return markpats

Marubatsu.count_markpats = count_markpats

下記は、いくつか の 局面 で、count_markpats を使って マークのパターン の数を 数える プログラムです。実行結果 から、正しく動作 することが 確認 できます。

from pprint import pprint
mb = Marubatsu()

print(mb)
pprint(mb.count_markpats())

mb.move(1, 1)
print(mb)
pprint(mb.count_markpats())

mb.move(0, 0)
print(mb)
pprint(mb.count_markpats())

mb.move(1, 0)
print(mb)
pprint(mb.count_markpats())

実行結果

Turn o
...
...
...

defaultdict(<class 'int'>, {Markpat(last_turn=0, turn=0, empty=3): 8})
Turn x
...
.O.
...

defaultdict(<class 'int'>,
            {Markpat(last_turn=0, turn=0, empty=3): 4,
             Markpat(last_turn=1, turn=0, empty=2): 4})
Turn o
X..
.o.
...

defaultdict(<class 'int'>,
            {Markpat(last_turn=0, turn=0, empty=3): 2,
             Markpat(last_turn=0, turn=1, empty=2): 3,
             Markpat(last_turn=1, turn=0, empty=2): 2,
             Markpat(last_turn=1, turn=1, empty=1): 1})
Turn x
xO.
.o.
...

defaultdict(<class 'int'>,
            {Markpat(last_turn=0, turn=0, empty=3): 2,
             Markpat(last_turn=0, turn=1, empty=2): 1,
             Markpat(last_turn=1, turn=0, empty=2): 2,
             Markpat(last_turn=1, turn=1, empty=1): 2,
             Markpat(last_turn=2, turn=0, empty=1): 1})

ai9s の定義

count_markpats を 利用 することで、ai9s は 下記 のプログラムのように 定義 できます。修正点 は、評価値の修正 と、markpats の キーの値 を使って 判定を行う 点です。

• 7、11 行目：評価値 を 評価値の表 に合わせて 修正 する
• 15 行目：markpats の「自 0 敵 2 空 1」の キーの数 が 正の場合 に、相手 が 勝利できる と 判定 するように 修正 する
• 18 行目：markpats の「自 2 敵 0 空 1」の キーの数 が 2 以上 の場合は、次 の 自分の手番 で自分が 必ず勝利できる と 判定 して、評価値 として 2 を 返す
• 21 行目：markpats の「自 0 敵 2 空 1」の キーの数 が 1 の場合 に、次 の 自分の手番 で自分が 勝利できる と 判定 するように 修正 する

 1  from ai import ai_by_score
 2
 3  def ai9s(mb, debug=False):
 4     def eval_func(mb):
 5          # 真ん中のマスに着手している場合は、評価値として 4 を返す
 6          if mb.last_move == (1, 1):
 7              return 4
 8   
 9          # 自分が勝利している場合は、評価値として 3 を返す
10          if mb.status == mb.last_turn:
11              return 3
12
13          markpats = mb.count_markpats()
14          # 相手が勝利できる場合は評価値として -1 を返す
15          if markpats[Markpat(last_turn=0, turn=2, empty=1)] > 0:
16              return -1
17          # 次の自分の手番で自分が必ず勝利できる場合は評価値として 2 を返す
18          elif markpats[Markpat(last_turn=2, turn=0, empty=1)] >= 2:
19              return 2
20          # 次の自分の手番で自分が勝利できる場合は評価値として 1 を返す
21          elif markpats[Markpat(last_turn=2, turn=0, empty=1)] == 1:
22              return 1
23          # それ以外の場合は評価値として 0 を返す
24          else:
25              return 0
26
27      return ai_by_score(mb, eval_func, debug=debug) 

行番号のないプログラム

from ai import ai_by_score

def ai9s(mb, debug=False):
    def eval_func(mb):
        # 真ん中のマスに着手している場合は、評価値として 4 を返す
        if mb.last_move == (1, 1):
            return 4
    
        # 自分が勝利している場合は、評価値として 3 を返す
        if mb.status == mb.last_turn:
            return 3

        markpats = mb.count_markpats()
        # 相手が勝利できる場合は評価値として -1 を返す
        if markpats[Markpat(last_turn=0, turn=2, empty=1)] > 0:
            return -1
        # 次の自分の手番で自分が必ず勝利できる場合は評価値として 2 を返す
        elif markpats[Markpat(last_turn=2, turn=0, empty=1)] >= 2:
            return 2
        # 次の自分の手番で自分が勝利できる場合は評価値として 1 を返す
        elif markpats[Markpat(last_turn=2, turn=0, empty=1)] == 1:
            return 1
        # それ以外の場合は評価値として 0 を返す
        else:
            return 0

    return ai_by_score(mb, eval_func, debug=debug) 

修正箇所

from ai import ai_by_score

-def ai8s(mb, debug=False):
+def ai9s(mb, debug=False):
    def eval_func(mb):
        # 真ん中のマスに着手している場合は、評価値として 4 を返す
        if mb.last_move == (1, 1):
-           return 3
+           return 4
    
        # 自分が勝利している場合は、評価値として 3 を返す
        if mb.status == mb.last_turn:
-           return 2
+           return 3

        markpats = mb.count_markpats()
        # 相手が勝利できる場合は評価値として -1 を返す
-       if Markpat(last_turn=0, turn=2, empty=1) in markpats:
+       if markpats[Markpat(last_turn=0, turn=2, empty=1)] > 0:
            return -1
        # 次の自分の手番で自分が必ず勝利できる場合は評価値として 2 を返す
-       elif Markpat(last_turn=2, turn=0, empty=1) in markpats:
+       elif markpats[Markpat(last_turn=2, turn=0, empty=1)] >= 2:
-           return 1
+           return 2
        # 次の自分の手番で自分が勝利できる場合は評価値として 1 を返す
+       elif markpats[Markpat(last_turn=2, turn=0, empty=1)] == 1:
+           return 1
        # それ以外の場合は評価値として 0 を返す
        else:
            return 0

    return ai_by_score(mb, eval_func, debug=debug) 

ai2 と ai8s との対戦

基準となる ai2 と、これまで に作成した 最強の AI である ai8s と対戦することにします。まず、下記のプログラムで ai2 と対戦します。

from ai import ai_match, ai2, ai8s

ai_match(ai=[ai9s, ai2])

実行結果（実行結果はランダムなので下記とは異なる場合があります）

ai9s VS ai2
count     win    lose    draw
o        9867      15     118
x        8961     237     802
total   18828     252     920

ratio     win    lose    draw
o       98.7%    0.1%    1.2%
x       89.6%    2.4%    8.0%
total   94.1%    1.3%    4.6%

下記は、ai8s VS ai2 と ai9s VS ai2 の対戦結果の表です。ai2 に対して、ai9s のほうが、ai8s より 勝率が高くなる ことが確認できます。

関数名	o 勝	o 負	o 分	x 勝	x 負	x 分	勝	負	分
ai8s	97.3	1.5	1.3	86.1	8.5	5.4	91.7	5.0	3.3
ai9s	98.7	0.1	1.2	89.6	2.4	8.0	94.1	1.3	4.6

次に、ai8s と 対戦 を行います。実行結果 の 通算成績 から、ai9s が ai8s に 対して強くなっており、新しい条件 の 有効性 が 確認 できました。

ai_match(ai=[ai9s, ai8s])

実行結果（実行結果はランダムなので下記とは異なる場合があります）

ai9s VS ai8s
count     win    lose    draw
o        5019     397    4584
x         409    3365    6226
total    5428    3762   10810

ratio     win    lose    draw
o       50.2%    4.0%   45.8%
x        4.1%   33.7%   62.3%
total   27.1%   18.8%   54.0%

マークのパターンの考察

これまでのルール では、マークのパターン のうち、「自 0 敵 2 空 1」と「自 2 敵 0 空 1」のみを利用 してきましたが、他 の マークのパターン も 局面の状況 を 表している と 考えられる ので、それぞれ の マークのパターン の 考察 を行うことにします。

下記 の 表 は、マークのパターン の 一覧 で、10 種 類ある事が分かります。それぞれ の マークのパターン の 性質 がどのようなものであるかについて、少し考えてみて下さい。

自	敵	空
3	0	0
2	1	0
2	0	1
1	2	0
1	1	1
1	0	2
0	3	0
0	2	1
0	1	2
0	0	3

「自 3 敵 0 空 0」

このマークのパターンは、自分が勝利 していることを 表します が、自分の勝利 は、status 属性 で 判定済 なので、このマークのパターンを 考慮 する 必要 は ありません。

「自 0 敵 3 空 0」

このマークのパターンは、相手が勝利 していることを 表します が、〇×ゲーム は、自分の着手 によって 相手が勝利 することは あり得ない ので、このマークのパターンが 出現 することは ありません。従って、このマークのパターンを 考慮 する 必要 は ありません。

「自 2 敵 0 空 1」

このマークのパターンは、今回の記事 で 考察済 です。なお、このマークのパターンが 2 つ以上 ある 場合 に、その 数を区別 する 必要があるか どうかが気になる人がいるかもしれないので補足します。このマークのパターンが 2 つ以上 ある場合は、いくつであっても 次の自分の手番で 自分が勝利できる ことに 変わりはありません ので、このマークのパターンが 2 つ以上 の場合の 数の違い を 区別しなくても、AI の強さ に 影響 は 与えません。

「自 0 敵 2 空 1」

このマークのパターンは既に ルールの条件 に 組み込まれています。このマークのパターンが 1 つ以上 ある場合も、上記と同様に、いくつであっても、次の相手の手番で 相手が勝利できる ことに 変わりがない と思う人が多いのではないかと思います。実際 には AI の強さ に 少し だけ 影響を与える のですが、その点については次回の記事で説明することにします。興味がある方は、どのような影響を与えるかについて少し考えてみて下さい。

自と敵がのマークが両方あるパターン

「自 2 敵 1 空 0」、「自 1 敵 1 空 1」、「自 1 敵 2 空 0」の 3 種類 のマークのパターンは、その ライン に 自分 と 敵 の 両方のマーク が 配置されている ことを表します。〇×ゲーム は、一度配置 した マーク は ゲームが終了 するまで 変化しない ので、これらの マークのパターンの ライン は、今後 のゲームの 勝敗 に 影響を与えない可能性が高い ことが 考察 できます。従って、このマークのパターンの 数 は AIの強さ に 影響を及ぼさない可能性が高い ことが 推測 できます。なお、絶対 に 影響を及ぼさない という 証明 は 行っていない ので、あくまで 可能性が高い に 過ぎない 点に 注意 して下さい。

「自 0 敵 0 空 3」

このマークのパターンの ライン は、自分 と 相手 の 両方 が、今後 勝利できる可能性がある ラインです。従って、このマークのパターンの 数 が どちらか に 有利に働く ということは なさそう なので、AI の強さ に 影響 を 及ぼさない可能性が高い ことが 推測 できます。

「自 1 敵 0 空 2」

〇×ゲーム に 勝利 するためには、「自 2 敵 0 空 1」が 存在する着手 を行う 必要 がありますが、そのため には、自分の 前の手番 で「自 1 敵 0 空 2」が 存在する着手 を 行う必要 があります。従って、ゲームが終了するまでの間 に 必ず「自 1 敵 0 空 2」が 存在する着手 を行うことが、〇×ゲーム に 勝利するため の 必要条件 であることが分かります。

ただし、「自 2 敵 0 空 1」の場合と同様に、どのタイミング で「自 1 敵 0 空 2」が 存在する着手 を 行う必要 があるかまでは わかりません ので、必要条件 では ありません が、「自 1 敵 0 空 2」が 存在する着手 を すぐに行う という条件を考えることにします。

次に、「自 1 敵 0 空 2」の 数 を 考察 することにします。「自 1 敵 0 空 2」の 数 が多ければ 多い程、次 の 自分の手番 で、「自 1 敵 0 空 2」が 残っている可能性が高くなる ので、「自 1 敵 0 空 2」の 数 が 多い ことが 望ましい ことが 推測 できます。

また、「自 1 敵 0 空 2」の 数を増やす ということは、相手が勝つ ことが できるライン を 減らす ことにも つながります。そのような理由 からも、「自 1 敵 0 空 2」の 数 が 多い ことが 望ましい ことが 推測 できます。

「自 0 敵 1 空 2」

相手の立場 から考えると、このマークのパターンは「自 1 敵 0 空 2」になるので、「自 0 敵 1 空 2」の 数が多い ということは、相手の勝利 の 可能性が高くなる ことが 推測 できます。従って、「自 0 敵 1 空 2」の 数 が 少ない ことが 望ましい ことが 推測 できます。

マークのパターンの考察のまとめ

下記 は、上記の考察 を 表にまとめた ものです。

自	敵	空	考察
3	0	0	status 属性 で 確認済 なので、考慮する必要はない
0	3	0	あり得ない ので 考慮する必要はない
2	0	1	既 に ルール に 組み込まれている ので新しく 考慮する必要はない
0	2	1	既 に ルール に 組み込まれている ので新しく 考慮する必要はない
2	1	0	どちらの 勝利 にも 影響しない可能性が高い ので 考慮する必要はない
1	2	0	どちらの 勝利 にも 影響しない可能性が高い ので 考慮する必要はない
1	1	1	どちらの 勝利 にも 影響しない可能性が高い ので 考慮する必要はない
0	0	3	どちらの 勝利 にも 影響しない可能性が高い ので 考慮する必要はない
1	0	2	多いほう が 有利 になる
0	1	2	少ないほう が 有利 になる

上記の表 から、以下 の 2 つ の 条件 を ルールに組み込む ことで AI が 強くなる可能性が高い ことが 推測される ので、条件に組み込む ことにします。なお、いずれの条件 も、必要条件 でも 十分条件 でも ありません ので、組み込む ことで 弱くなる可能性 があります。

• 「自 1 敵 0 空 2」の 数 が 最も多い 着手を行う
• 「自 0 敵 1 空 2」の 数 が 最も少ない 着手を行う

ルール 10

まず、『「自 1 敵 0 空 2」の 数 が 最も多い 着手を行う』という 条件 を ルール 9 に 追加 した ルール 10 を 定義 する事にします。どのように定義すればよいかについて少し考えてみて下さい。

複数の条件が同時に満たされる場合のルール

ルール 9 まで は、すべての条件 には 明確な理由 を元にした 優先順位 があり、上位の条件 が 満たされた時点 で 評価値が決定 され、それより 下位の条件 は 考慮されません でした。

一方、ルール 9 の『「自 2 敵 0 空 1」が 1 つ存在 する』と、『「自 1 敵 0 空 2」の 数 が 最も多い』という 条件 が 同時 に 満たされた場合 に、どちらを優先すればよいか については、明確 では ありません。従って、ルール 10 は、下記のように、同じ優先順位 に 複数の条件 が 存在する ように 定義 する 必要 があります。このような場合に、どのように評価値 を 設定 すればよいかについて少し考えてみて下さい。なお、長くて表が見づらいので、条件の内容を簡略化しました。

順位	条件	種類
1	真ん中 のマスに 優先的 に 着手 する
2	勝てる場合 に 勝つ	十分条件
3	相手 が 勝利できる 着手を 行わない	必要条件
4	「自 2 敵 0 空 1」が 2 つ以上存在 する着手を行う	十分条件
5	「自 2 敵 0 空 1」が 1 つ存在 する着手を行う 「自 1 敵 0 空 2」が 最も多い 着手を行う
6	ランダム なマスに 着手 する

同じ優先順位の条件に対する評価値の設定方法

同じ優先順位 の 条件 が 複数存在 する場合に、どのような 評価値 を 設定するか については、下記のように、それぞれの条件 が 満たされる場合 と 満たされない場合 の すべての組み合わせ を 表 にして 考察 すると良いでしょう。

	「自 2 敵 0 空 1」が 1 つ	「自 1 敵 0 空 2」が最も多い
組み合わせ 1	×	×
組み合わせ 2	〇	×
組み合わせ 3	×	〇
組み合わせ 4	〇	〇

片方の条件 が 同じ であれば、明らかに もう片方の条件 が 満たされる方 の 評価値 を 高くする必要 があります。そのため、上記の表 から、それぞれの組み合わせ に対する 評価値 には、下記 のような 関係がある ことが 分かります。

• 組み合わせ 1 の評価値 < 組み合わせ 2 の評価値 < 組み合わせ 4 の評価値
• 組み合わせ 1 の評価値 < 組み合わせ 3 の評価値 < 組み合わせ 4 の評価値

上記の条件 を 満たす ことができれば、それぞれ の 組み合わせ の 評価値 を どのように設定 しても 構いません。評価値の設定方法 について少し考えてみて下さい。

最も簡単 な 方法 は、それぞれ の 条件 が 単独 で 満たされる場合 の 正の評価値 を 個別に設定 し、組み合わせ の 評価値を計算 する際に、合計を計算 するという 方法 でしょう。

よりふさわしい方法があれば、そちらを採用しても構いません。

例えば、『「自 2 敵 0 空 1」が 1 つ存在 する』が 満たされる場合 の 評価値 を A、『「自 1 敵 0 空 2」の 数 が 最も多い』が 満たされる場合 の 評価値 を B と 設定 した場合は、それぞれ の 組み合わせ の 評価値 は 下記の表 のように、簡単な方法 で 計算 できます。なお、A と B は 正の数 とし、具体的な値 は この後 で 設定 します。

	「自 2 敵 0 空 1」が 1 つ	「自 1 敵 0 空 2」が最も多い	評価値
組み合わせ 1	×	×	0
組み合わせ 2	〇	×	A
組み合わせ 3	×	〇	B
組み合わせ 4	〇	〇	A + B

先程 の、それぞれ の 組み合わせ の 評価値 の 関係 を表す 式 に、上記 の 評価値 を 当てはめる と 下記 の 式 になります。A と B は 正の値 なので、下記 の 2 つ の 式 が 常に正しくなる ことは 明らか でしょう。

• 0 < A < A + B
• 0 < B < A + B

具体的な評価値の設定方法

上記の方針 で 評価値を設定 する場合は、A と B に どのような値 を 設定 すればよいかについて 考える必要 があります。A と B は それぞれ の 条件 の 評価値 を表すので、下記の表 のように、それぞれの条件 の 重要度 を 考慮した評価値 を 設定 する 必要 があります。

A と B の関係	A と B の重要度
A > B	A の条件 のほうが、B の条件より も 重要度 が 高い
A = B	A の条件 と B の条件 の 重要度 が 同程度 か、関係 が 不明 である
A < B	A の条件 のほうが、B の条件より も 重要度 が 低い

今回の場合、『「自 2 敵 0 空 1」が 1 つ存在 する』と『「自 1 敵 0 空 2」が 最も多い』の どちら の条件が 重要であるか は わかっていません。また、仮に 片方が重要 だとしても、どれくらい重要 であるかは わからない ことが 良くあります。そのような場合 は、以下 のような 試行錯誤 による方法で 評価値 を 設定 するのが 一般的 です。

1. とりあえず おおざっぱに 評価値 を 設定 して AI を実装 する
2. 実装した AI と 他の AI を 対戦 させて、強さを評価 する
3. A または B の 評価値 を 少し変化 させて、対戦 させる
4. 手順 2 と 3 を 何度も繰り返し、最も成績が良い 評価値の 組み合わせ を 採用 する

試行錯誤 の 回数 が 多くなればなるほど、手間 と 時間 が 増大 します。そのため、上記の 手順 3 で、効率よく A や B の 評価値 を 変化させながら、上記の手順 を 行う必要 があります。その方法については、機械学習の手法を紹介する際に説明する予定です。

今回の条件 の場合は、上記の試行錯誤 は 数回だけ行う ことにします。

まず、A の 評価値 として、とりあえず 1 を設定 することにします。次に B の評価値 を 決める必要 がありますが、これまでのように、特定の数 を 設定 することは できません。その理由について少し考えてみて下さい。

数を考慮する評価値の設定方法

ルール 9 まで の 条件 では、その 条件が満たされるかどうか で 評価値が決まりました。一方、ルール 10 で 追加 する『「自 1 敵 0 空 2」が 最も多い』という 条件 は、マークのパターン の 数 が 多いほど 評価値が 大きくなる ように 評価値を設定 する 必要 があります。

そのような場合に 最も簡単 な 評価値 の 計算方法 は、$a$ を 正の数、$x$ を マークのパターン の 数 とした場合に、下記の式 で 計算 するという 方法 です。

$評価値 = a × x$

最もわかりやすい のは、$a$ に 1 を 設定 する場合で、その場合の 評価値 は、マークのパターンの数 を表す $x$ になります。$x$ が 増えれば、評価値も増える ので、「自 1 敵 0 空 2」が 最も多い場合 の 評価値 が 最も高くなる ことは 明らか でしょう。

今回は、B の 評価値 として、この $x$ を 採用 することにします。

$x$ が 増えれば、評価値 が 増える という 条件が満たされる のであれば、評価値 の 式 は どのような式 でも 構いません。例えば、下記 の 式 でも かまいません が、特に理由がない限り、先程紹介した 最も簡単な式 を 採用 するのが 一般的 でしょう。

$評価値 = a × x^2$

ルール 10 の評価値の設定

下記 は、上記を元 に、ルール 10 の 評価値を設定 した表です。「個別」の列には、同じ優先順位 の 条件 の 個別の評価値 を記述します。「評価値」の列が ？ になっているのは、新しい条件 を 追加 したため、評価値 を 設定し直す 必要があるためです。？ に 評価値 を 設定する方法 について少し考えてみて下さい。

順位	局面の状況	個別	評価値
1	真ん中のマスに着手している		？
2	自分が勝利している		？
4	「自 2 敵 0 空 1」が 2 つ以上存在する		？
5	「自 2 敵 0 空 1」が 1 つ存在する 「自 1 敵 0 空 2」が x 個存在する	1 x	？
6	「自 2 敵 0 空 1」が存在しない		？
3	相手が勝利できる		？

『「自 2 敵 0 空 1」が存在しない』場合の評価値

まず、優先順位 が 6 の『「自 2 敵 0 空 1」が 存在しない』場合の 評価値 について考えることにします。この条件 は、優先順位 が 6 の所に 記述 されていますが、実際 には、優先順位 が 5 の『「自 1 敵 0 空 2」が x 個存在 する』という 条件 と 同時に満たされる 条件で、どちら の条件が 優先度が高いか は わかっていません。従って、この条件 は 優先順位 が 5 の 条件の中 に 入れる必要 があります。

『「自 2 敵 0 空 1」が 存在しない』という条件は、『「自 2 敵 0 空 1」が 1 つ存在 する』という 条件 が 満たされなかった場合 の 条件 なので、この条件が満たされる場合の 評価値 は 0 になります。下記 は、そのように修正 した 表 です。

順位	局面の状況	個別	評価値
1	真ん中のマスに着手している		？
2	自分が勝利している		？
4	「自 2 敵 0 空 1」が 2 つ以上存在する		？
5	「自 2 敵 0 空 1」が 1 つ存在する 「自 2 敵 0 空 1」が存在しない 「自 1 敵 0 空 2」が x 個存在する	1 0 x	？
3	相手が勝利できる		？

個別 の 評価値 が 0 の 条件 は、評価値の計算 に 影響を与えない ので、表に記述 する 意味 が ありません。そのため、上記の表 は、下記 のように まとめる ことが できます。

順位	局面の状況	個別	評価値
1	真ん中のマスに着手している		？
2	自分が勝利している		？
4	「自 2 敵 0 空 1」が 2 つ以上存在する		？
5	「自 2 敵 0 空 1」が 1 つ存在する 「自 1 敵 0 空 2」が x 個存在する	1 x	？
3	相手が勝利できる		？

評価値の範囲の計算

表の 評価値 の 列 の 値 は 、上から大きい順 に 並べる必要 があります。現時点 では、優先順位 が 5 の 個別の評価値のみ が 決まっている ので、その 評価値 について 考察 します。

優先順位 が 5 の 評価値 は、個別 の 評価値 の 合計 になので、評価値の値 は 状況 によって 変化します が、その 範囲 を 計算 することは 可能 です。

下記の、それぞれ の 組み合わせ の 評価値 の 関係 を表す 式 から、評価値 の 最小値 が 0 で、最大値 が A + B であることが分かります。

• 0 < A < A + B
• 0 < B < A + B

今回の場合は、A が 1 で、B が x なので、優先順位 が 5 の 評価値 の 範囲 は 0 ～ 1 + x になります。下記は、そのことを 表に加えた ものです。

順位	局面の状況	個別	評価値
1	真ん中のマスに着手している		？
2	自分が勝利している		？
4	「自 2 敵 0 空 1」が 2 つ以上存在する		？
5	「自 2 敵 0 空 1」が 1 つ存在する 「自 1 敵 0 空 2」が x 個存在する	1 x	0 ～ 1 + x
3	相手が勝利できる		？

次に、範囲の中 に x という 変数 が 入っている ので、x が とる値 の 範囲 を 考える必要 があります。x は、「自 1 敵 0 空 2」の マークのパターン の 数 を表し、その 最大値 は、ラインの数 である 8 なので、x の 最大値 は 8 であることが わかります。

実際 には、相手も着手 を 行う ので、「自 1 敵 0 空 2」の 数 が 8 になる ことは ありません が、？ の 値を設定 するために、厳密 な x の範囲 を 計算 する 必要はない ので、8 として計算する ことにします。

下記は、優先順位 が 5 の 評価値の範囲 を 計算しやすい ように、個別の条件 の 評価値 の横に、それぞれの 範囲 を追加し、それを元に 評価値の範囲 を計算したものです。

順位	局面の状況	個別	評価値
1	真ん中のマスに着手している		？
2	自分が勝利している		？
4	「自 2 敵 0 空 1」が 2 つ以上存在する		？
5	「自 2 敵 0 空 1」が 1 つ存在する 「自 1 敵 0 空 2」が x 個存在する	1 (0～1) x (0～8)	0～9
3	相手が勝利できる		？

評価値の範囲 が 分かった ので、？ を 下記の表 のように 決める ことができます。

順位	局面の状況	個別	評価値
1	真ん中のマスに着手している		12
2	自分が勝利している		11
4	「自 2 敵 0 空 1」が 2 つ以上存在する		10
5	「自 2 敵 0 空 1」が 1 つ存在する 「自 1 敵 0 空 2」が x 個存在する	1 (0～1) x (0～8)	0～9
3	相手が勝利できる		-1

ai10s の定義

評価値 が 決まった ので、ai10s を 定義 します。

ai9s では、それぞれの 優先順位 の 条件の判定 を 1 つの if 文 で 行っていました が、ai10s では、優先順位 が 5 の 評価値 を 計算する前 にその if 文 を 終了する必要 があります。

その後で 同じ優先順位 が 5 の 条件 の 評価値 を 加算 する 計算を行う 際には、下記のプログラムのように、評価値 を 計算する変数 を 用意 し、条件が満たされる たびに 加算 し、最後に 計算した評価値 を return 文で返す という処理を行います。

• 5、9、17 行目：評価値 を表に合わせて 修正 する
• 20 行目：評価値の合計 を 計算 する局所変数 score を 0 で 初期化 する
• 22、23 行目：「自 2 敵 0 空 1」が 1 つ存在 する場合に 評価値 に 1 を加算 する
• 25 行目：評価値 に「自 1 敵 0 空 2」の 個数 を 加算 する
• 28 行目：計算した評価値 を 返り値 として 返す

 1  def ai10s(mb, debug=False):
 2      def eval_func(mb):
 3          # 真ん中のマスに着手している場合は、評価値として 12 を返す
 4          if mb.last_move == (1, 1):
 5              return 12
 6   
 7          # 自分が勝利している場合は、評価値として 11 を返す
 8          if mb.status == mb.last_turn:
 9              return 11
10
11          markpats = mb.count_markpats()
12          # 相手が勝利できる場合は評価値として -1 を返す
13          if markpats[Markpat(last_turn=0, turn=2, empty=1)] > 0:
14              return -1
15          # 次の自分の手番で自分が必ず勝利できる場合は評価値として 10 を返す
16          elif markpats[Markpat(last_turn=2, turn=0, empty=1)] >= 2:
17              return 10
18
19          # 評価値の合計を計算する変数を 0 で初期化する
20          score = 0
21          # 次の自分の手番で自分が勝利できる場合は評価値に 1 を加算する
22          if markpats[Markpat(last_turn=2, turn=0, empty=1)] == 1:
23              score += 1
24          # 「自 1 敵 0 空 2」の数だけ、評価値を加算する
25          score += markpats[Markpat(last_turn=1, turn=0, empty=2)]
26        
27          # 計算した評価値を返す
28          return score
29
30      return ai_by_score(mb, eval_func, debug=debug) 

行番号のないプログラム

def ai10s(mb, debug=False):
    def eval_func(mb):      
        # 真ん中のマスに着手している場合は、評価値として 12 を返す
        if mb.last_move == (1, 1):
            return 12
    
        # 自分が勝利している場合は、評価値として 11 を返す
        if mb.status == mb.last_turn:
            return 11

        markpats = mb.count_markpats()
        # 相手が勝利できる場合は評価値として -1 を返す
        if markpats[Markpat(last_turn=0, turn=2, empty=1)] > 0:
            return -1
        # 次の自分の手番で自分が必ず勝利できる場合は評価値として 10 を返す
        elif markpats[Markpat(last_turn=2, turn=0, empty=1)] >= 2:
            return 10

        # 評価値の合計を計算する変数を 0 で初期化する
        score = 0        
        # 次の自分の手番で自分が勝利できる場合は評価値に 1 を加算する
        if markpats[Markpat(last_turn=2, turn=0, empty=1)] == 1:
            score += 1
        # 「自 1 敵 0 空 2」の数だけ、評価値を加算する
        score += markpats[Markpat(last_turn=1, turn=0, empty=2)]
        
        # 計算した評価値を返す
        return score

    return ai_by_score(mb, eval_func, debug=debug) 

修正箇所

-def ai9s(mb, debug=False):
+def ai10s(mb, debug=False):
    def eval_func(mb):       
        # 真ん中のマスに着手している場合は、評価値として 12 を返す
        if mb.last_move == (1, 1):
-           return 4
+           return 12
    
        # 自分が勝利している場合は、評価値として 11 を返す
        if mb.status == mb.last_turn:
-           return 3
+           return 11

        markpats = mb.count_markpats()
        # 相手が勝利できる場合は評価値として -1 を返す
        if markpats[Markpat(last_turn=0, turn=2, empty=1)] > 0:
            return -1
        # 次の自分の手番で自分が必ず勝利できる場合は評価値として 10 を返す
        elif markpats[Markpat(last_turn=2, turn=0, empty=1)] >= 2:
-           return 2
+           return 10
        # 次の自分の手番で自分が勝利できる場合は評価値として 1 を返す
-       elif markpats[Markpat(last_turn=2, turn=0, empty=1)] == 1:
-           return 1
-       # それ以外の場合は評価値として 0 を返す
-       else:
-           return 0

        # 評価値の合計を計算する変数を 0 で初期化する
+       score = 0
        # 次の自分の手番で自分が勝利できる場合は評価値に 1 を加算する
+       if markpats[Markpat(last_turn=2, turn=0, empty=1)] == 1:
+           score += 1
        # 「自 1 敵 0 空 2」の数だけ、評価値を加算する
+       score += markpats[Markpat(last_turn=1, turn=0, empty=2)]       
        # 計算した評価値を返す
+       return score

    return ai_by_score(mb, eval_func, debug=debug) 

ai2 と ai9s との対戦

基準となる ai2 と、これまで に作成した 最強の AI である ai9s と対戦することにします。まず、下記のプログラムで ai2 と対戦します。

ai_match(ai=[ai10s, ai2])

実行結果（実行結果はランダムなので下記とは異なる場合があります）

ai10s VS ai2
count     win    lose    draw
o        9737       0     263
x        8564     263    1173
total   18301     263    1436

ratio     win    lose    draw
o       97.4%    0.0%    2.6%
x       85.6%    2.6%   11.7%
total   91.5%    1.3%    7.2%

下記は、ai9s VS ai2 と ai10s VS ai2 の 対戦結果 の 表 です。ai2 に対して、ai10s のほうが、ai9s より 勝率が若干低くなる ことが 確認 できます。このことから、新しい条件 が ai2 に対して 何らかの理由 で 若干不利 になる 可能性 があります。

関数名	o 勝	o 負	o 分	x 勝	x 負	x 分	勝	負	分
ai9s	98.7	0.1	1.2	89.6	2.4	8.0	94.1	1.3	4.6
ai10s	97.4	0.0	2.6	85.6	2.6	11.7	91.5	1.3	7.2

次に、ai9s と 対戦 を行います。実行結果 の 通算成績 の 勝率 が 約 40 %、敗率 が 0 % となることから、ai10s が ai9s に 対して 大幅に強くなっている ことが確認できます。特に、ai9s に対する 敗率 が 0% は、これまでにない 大きな成果 であると言えるでしょう。

ai_match(ai=[ai10s, ai9s])

実行結果（実行結果はランダムなので下記とは異なる場合があります）

ai10s VS ai9s
count     win    lose    draw
o        7478       0    2522
x         791       0    9209
total    8269       0   11731

ratio     win    lose    draw
o       74.8%    0.0%   25.2%
x        7.9%    0.0%   92.1%
total   41.3%    0.0%   58.7%

評価値の調整

先程、評価値 の 設定方法 として、下記 のような 方法を紹介 しました。

1. とりあえず おおざっぱに 評価値 を 設定 して AI を実装 する
2. 実装した AI と 他の AI を 対戦 させて、強さを評価 する
3. A または B の 評価値 を 少し変化 させて、対戦 させる
4. 手順 2 と 3 を 何度も繰り返し、最も成績が良い 評価値の 組み合わせ を 採用 する

そこで、「自 2 敵 0 空 1」が 1 つ存在 する場合の 評価値 を 1 から 5 に 変えてみる ことにします。その際に、ai10s の下記の 3 行目 の score += 1 を score += 5 に 変えるだけで良い のではないかと 思う人がいるかもしれません が、それだけ では バグが発生 してしまいます。どのようなバグが発生するかについて少し考えてみて下さい。

        # 次の自分の手番で自分が勝利できる場合は評価値に 1 を加算する
        if markpats[Markpat(last_turn=2, turn=0, empty=1)] == 1:
            score += 1

下記は、「自 2 敵 0 空 1」が 1 つ存在 する場合の 評価値 を 5 に設定 した場合の 表 です。

順位	局面の状況	個別	評価値
1	真ん中のマスに着手している		12
2	自分が勝利している		11
4	「自 2 敵 0 空 1」が 2 つ以上存在する		10
5	「自 2 敵 0 空 1」が 1 つ存在する 「自 1 敵 0 空 2」が x 個存在する	5 (0～5) x (0～8)	0～13
3	相手が勝利できる		-1

表から、優先順位 が 5 の 評価値 の 範囲 が 0 ~ 9 から、0 ~ 13 に 変化 したことがわかりますが、それ以外 の 優先順位 の 評価値 を 変えていない ので、優先順位 が 5 の 評価値 が、それより 上の行 の 評価値より も 高く なってしまう 可能性が生じています。

下記は、新しい評価値 の 範囲 に 応じて、他の評価値 を 修正 した 表 です。修正する際 に、下記のように それぞれ の 優先順位 の 評価値 の 間隔 を 100 のように 大きな値にする ことで、評価値 の 計算式 を 多少修正 した場合でも、上下の行 の 評価値 の 大小関係 が 壊れにくくなる という 工夫 を行っています。

順位	局面の状況	個別	評価値
1	真ん中のマスに着手している		300
2	自分が勝利している		200
4	「自 2 敵 0 空 1」が 2 つ以上存在する		100
5	「自 2 敵 0 空 1」が 1 つ存在する 「自 1 敵 0 空 2」が x 個存在する	5 (0～5) x (0～8)	0～13
3	相手が勝利できる		-100

下記のプログラムは、上記の評価値 を計算するように 修正 した ai10s です。

• 5、9、14，17 行目：評価値 を 修正 した
• 23 行目：評価値 の 加算 を 1 から 5 に 修正 した

 1  def ai10s(mb, debug=False):
 2      def eval_func(mb):      
 3          # 真ん中のマスに着手している場合は、評価値として 300 を返す
 4          if mb.last_move == (1, 1):
 5              return 300
 6   
 7          # 自分が勝利している場合は、評価値として 200 を返す
 8          if mb.status == mb.last_turn:
 9              return 200
10
11          markpats = mb.count_markpats()
12          # 相手が勝利できる場合は評価値として -100 を返す
13          if markpats[Markpat(last_turn=0, turn=2, empty=1)] > 0:
14              return -100
15          # 次の自分の手番で自分が必ず勝利できる場合は評価値として 100 を返す
16          elif markpats[Markpat(last_turn=2, turn=0, empty=1)] >= 2:
17              return 100
18
19          # 評価値の合計を計算する変数を 0 で初期化する
20          score = 0        
21          # 次の自分の手番で自分が勝利できる場合は評価値に 5 を加算する
22          if markpats[Markpat(last_turn=2, turn=0, empty=1)] == 1:
23              score += 5
24          # 「自 1 敵 0 空 2」の数だけ、評価値を加算する
25          score += markpats[Markpat(last_turn=1, turn=0, empty=2)]
26        
27          # 計算した評価値を返す
28          return score
29
30      return ai_by_score(mb, eval_func, debug=debug)

行番号のないプログラム

def ai10s(mb, debug=False):
    def eval_func(mb):      
        # 真ん中のマスに着手している場合は、評価値として 300 を返す
        if mb.last_move == (1, 1):
            return 300
    
        # 自分が勝利している場合は、評価値として 200 を返す
        if mb.status == mb.last_turn:
            return 200

        markpats = mb.count_markpats()
        # 相手が勝利できる場合は評価値として -100 を返す
        if markpats[Markpat(last_turn=0, turn=2, empty=1)] > 0:
            return -100
        # 次の自分の手番で自分が必ず勝利できる場合は評価値として 100 を返す
        elif markpats[Markpat(last_turn=2, turn=0, empty=1)] >= 2:
            return 100

        # 評価値の合計を計算する変数を 0 で初期化する
        score = 0        
        # 次の自分の手番で自分が勝利できる場合は評価値に 5 を加算する
        if markpats[Markpat(last_turn=2, turn=0, empty=1)] == 1:
            score += 5
        # 「自 1 敵 0 空 2」の数だけ、評価値を加算する
        score += markpats[Markpat(last_turn=1, turn=0, empty=2)]
        
        # 計算した評価値を返す
        return score

    return ai_by_score(mb, eval_func, debug=debug)

修正箇所

def ai10s(mb, debug=False):
    def eval_func(mb):      
        # 真ん中のマスに着手している場合は、評価値として 300 を返す
        if mb.last_move == (1, 1):
-           return 12
+           return 300
    
        # 自分が勝利している場合は、評価値として 200 を返す
        if mb.status == mb.last_turn:
-           return 11
+           return 200

        markpats = mb.count_markpats()
        # 相手が勝利できる場合は評価値として -100 を返す
        if markpats[Markpat(last_turn=0, turn=2, empty=1)] > 0:
-           return -1
+           return -100
        # 次の自分の手番で自分が必ず勝利できる場合は評価値として 100 を返す
        elif markpats[Markpat(last_turn=2, turn=0, empty=1)] >= 2:
-           return 10
+           return 100

        # 評価値の合計を計算する変数を 0 で初期化する
        score = 0        
        # 次の自分の手番で自分が勝利できる場合は評価値に 5 を加算する
        if markpats[Markpat(last_turn=2, turn=0, empty=1)] == 1:
-           score += 1
+           score += 5
        # 「自 1 敵 0 空 2」の数だけ、評価値を加算する
        score += markpats[Markpat(last_turn=1, turn=0, empty=2)]
        
        # 計算した評価値を返す
        return score

    return ai_by_score(mb, eval_func, debug=debug)

修正した ai10s と ai2、ai9s との対戦

修正した ai10s で ai2、ai9s と 対戦 することにします。まず、下記のプログラムで ai2 と対戦します。

ai_match(ai=[ai10s, ai2])

実行結果（実行結果はランダムなので下記とは異なる場合があります）

ai10s VS ai2
count     win    lose    draw
o        9904       0      96
x        9002     305     693
total   18906     305     789

ratio     win    lose    draw
o       99.0%    0.0%    1.0%
x       90.0%    3.0%    6.9%
total   94.5%    1.5%    3.9%

下記は、先程の ai9s VS ai2 と ai10s VS ai2 の対戦結果に、今回の対戦結果 を 加えた表 です。今回の対戦結果では、ai9s VS ai2 とほぼ同じ成績になることが分かります。

関数名	o 勝	o 負	o 分	x 勝	x 負	x 分	勝	負	分
ai9s	98.7	0.1	1.2	89.6	2.4	8.0	94.1	1.3	4.6
ai10s(評価値 1)	97.4	0.0	2.6	85.6	2.6	11.7	91.5	1.3	7.2
ai10s(評価値 5)	99.0	0.0	1.0	90.0	3.0	6.9	94.5	1.5	3.9

次に、ai9s と 対戦 を行います。

ai_match(ai=[ai10s, ai9s])

実行結果（実行結果はランダムなので下記とは異なる場合があります）

ai10s VS ai9s
count     win    lose    draw
o        4878       0    5122
x         802       0    9198
total    5680       0   14320

ratio     win    lose    draw
o       48.8%    0.0%   51.2%
x        8.0%    0.0%   92.0%
total   28.4%    0.0%   71.6%

下記は、先程の ai10s VS ai9s 対戦結果に、今回の対戦結果 を 加えた表 です。表から、相変わらず ai9s に対しては ai10s は 強いものの、評価値 を 5 とすることで、〇 を担当 した場合の 勝率 が かなり低くなる ことがわかります。このようなことが起きるのは、『「自 2 敵 0 空 1」が 1 つ存在する』場合の 評価値 を 高く設定しすぎた ことによって、『「自 2 敵 0 空 1」が 1 つ存在する』場合の 重要度 を、本来の重要度より も 高く見積もりすぎる という、過大評価 が行われてしまったせいです。

評価値	o 勝	o 負	o 分	x 勝	x 負	x 分	勝	負	分
1	74.8	0.0	25.2	7.9	0.0	92.1	41.3	0.0	58.7
5	48.8	0.0	51.2	8.0	0.0	92.0	28.4	0.0	71.6

適切 な 評価値 を 求める ために、評価値 を 2、3、4 に 設定 して ai2、ai9s と 対戦 を 行う ことにします。なお、プログラムと実行結果は長くなるので省略し、結果の表 だけを 示します。興味がある方は、自分でプログラムを修正して対戦を行ってみて下さい。

ai2 との 対戦結果

評価値	o 勝	o 負	o 分	x 勝	x 負	x 分	勝	負	分
1	97.4	0.0	2.6	85.6	2.6	11.7	91.5	1.3	7.2
2	98.7	0.0	1.3	90.8	2.8	6.4	94.7	1.4	3.8
3	98.8	0.0	1.2	90.1	3.1	6.8	94.5	1.5	4.0
4	98.9	0.0	1.1	90.3	2.9	6.8	94.6	1.5	3.9
5	99.0	0.0	1.0	90.0	3.0	6.9	94.5	1.5	3.9

ai9s との 対戦結果

評価値	o 勝	o 負	o 分	x 勝	x 負	x 分	勝	負	分
1	74.8	0.0	25.2	7.9	0.0	92.1	41.3	0.0	58.7
2	55.6	0.0	44.4	8.2	0.0	91.8	31.9	0.0	68.1
3	49.5	0.0	50.5	8.8	0.0	91.2	29.1	0.0	70.9
4	49.4	0.0	50.6	7.9	0.0	92.1	28.7	0.0	71.3
5	48.8	0.0	51.2	8.0	0.0	92.0	28.4	0.0	71.6

上記の結果から、ai2 に対しては、評価値 が 2 以上 であれば どれもほぼ同じ で、ai9s に対しては 評価値 が 1 の場合が 最も成績が良い ことが分かります。ai2 と ai9s では、最も成績が良い 評価値が 異なります が、このような場合は どちらかを選択 する 必要 があります。本記事 では、下記 のような 理由 で、評価値 として 1 を採用する ことにします。

• ai2 より かなり強い ai9s に対する 成績 の方が 重要 と 考えられる
• 評価値 を 2 以上 にすると、ai9s に対する 対戦成績 が 急激 に 悪くなる

評価値 は 整数 である 必要 は ありません。興味と余裕がある方は、評価値 に 1.5 や 2.5 などを 設定 して 対戦 させてみて下さい。さらに良い評価値 を 見つける ことが できるかも しれません。

ルール 11

次に、『「自 0 敵 1 空 2」が 最も少ない 着手を行う』という 条件 を ルール 10 に 追加 した ルール 11 を 定義 する事にします。この条件は、ルール 10 の 優先順位 が 5 の 条件の一つ として 追加 することができるので、ルール 11 は 下記の表 のように 定義 できます。

順位	条件	種類
1	真ん中 のマスに 優先的 に 着手 する
2	勝てる場合 に 勝つ	十分条件
3	相手 が 勝利できる 着手を 行わない	必要条件
4	「自 2 敵 0 空 1」が 2 つ以上存在 する着手を行う	十分条件
5	「自 2 敵 0 空 1」が 1 つ存在 する着手を行う 「自 1 敵 0 空 2」が 最も多い 着手を行う 「自 0 敵 1 空 2」が 最も少ない 着手を行う
6	ランダム なマスに 着手 する

評価値の設定

「自 0 敵 1 空 2」が 最も少ない 着手を 行うようにする ためには、「自 0 敵 1 空 2」の 数が多い程、評価値 を 低く計算 する必要があります。その方法は、簡単で「自 0 敵 1 空 2」の 数 を $x$ とした場合に、$評価値 = -x$ のように、負の評価値 を 計算 するように 式を設定 します。下記の表は、新しい 条件と評価値 を ルール 10 の 表に加えた ものです。

一般的 に 評価値 には、自分 が 有利な場合 は 正の値 を、自分が 不利な場合 は 負の値 を 設定します。

順位	局面の状況	個別	評価値
1	真ん中のマスに着手している		300
2	自分が勝利している		200
4	「自 2 敵 0 空 1」が 2 つ以上存在する		100
5	「自 2 敵 0 空 1」が 1 つ存在する 「自 1 敵 0 空 2」が x 個存在する 「自 0 敵 1 空 2」が y 個存在する	1 (0～1) x (0～8) -y (-8~0)	-8～9
3	相手が勝利できる		-100

優先順位 ごとの 評価値 の 間隔 を 大きくしておいた おかげで、優先順位 が 5 の 条件 に、新しい条件 を 追加 しても、他の優先順位 の 評価値 を 変更する必要 は ありません。

ai11s の定義と、ai2、ai10s との対戦

評価値 の 表 を元に、ai11s は 下記 のプログラムのように 定義 できます。なお、『「自 2 敵 0 空 1」が 1 つ存在する』場合の 評価値 は、1 に戻しました。

• 5、6 行目：「自 0 敵 1 空 2」が y 個存在 する場合に、評価値 から y を 減算 する

1  def ai11s(mb, debug=False):
2      def eval_func(mb):      
元と同じなので省略
3          # 「自 1 敵 0 空 2」の数だけ、評価値を加算する
4          score += markpats[Markpat(last_turn=1, turn=0, empty=2)]
5          # 「自 0 敵 1 空 2」の数だけ、評価値を減算する
6          score -= markpats[Markpat(last_turn=0, turn=1, empty=2)]
元と同じなので省略

行番号のないプログラム

def ai11s(mb, debug=False):
    def eval_func(mb):      
        # 真ん中のマスに着手している場合は、評価値として 300 を返す
        if mb.last_move == (1, 1):
            return 300
    
        # 自分が勝利している場合は、評価値として 200 を返す
        if mb.status == mb.last_turn:
            return 200

        markpats = mb.count_markpats()
        # 相手が勝利できる場合は評価値として -100 を返す
        if markpats[Markpat(last_turn=0, turn=2, empty=1)] > 0:
            return -100
        # 次の自分の手番で自分が必ず勝利できる場合は評価値として 100 を返す
        elif markpats[Markpat(last_turn=2, turn=0, empty=1)] >= 2:
            return 100

        # 評価値の合計を計算する変数を 0 で初期化する
        score = 0        
        # 次の自分の手番で自分が勝利できる場合は評価値に 1 を加算する
        if markpats[Markpat(last_turn=2, turn=0, empty=1)] == 1:
            score += 1
        # 「自 1 敵 0 空 2」の数だけ、評価値を加算する
        score += markpats[Markpat(last_turn=1, turn=0, empty=2)]
        # 「自 0 敵 1 空 2」の数だけ、評価値を減算する
        score -= markpats[Markpat(last_turn=0, turn=1, empty=2)]
        
        # 計算した評価値を返す
        return score

    return ai_by_score(mb, eval_func, debug=debug)

修正箇所

-def ai10s(mb, debug=False):
+def ai11s(mb, debug=False):
    def eval_func(mb):      
元と同じなので省略
        # 「自 1 敵 0 空 2」の数だけ、評価値を加算する
        score += markpats[Markpat(last_turn=1, turn=0, empty=2)]
+       # 「自 0 敵 1 空 2」の数だけ、評価値を減算する
+       score -= markpats[Markpat(last_turn=0, turn=1, empty=2)]
元と同じなので省略

ai11s の 強さ を 確認 するために、ai2、ai10s と 対戦 することにします。まず、下記のプログラムで ai2 と対戦します。

ai_match(ai=[ai11s, ai2])

実行結果（実行結果はランダムなので下記とは異なる場合があります）

ai11s VS ai2
count     win    lose    draw
o        9813       0     187
x        8251     193    1556
total   18064     193    1743

ratio     win    lose    draw
o       98.1%    0.0%    1.9%
x       82.5%    1.9%   15.6%
total   90.3%    1.0%    8.7%

下記は、ai11s VS ai2 と、評価値が 1 の場合の ai10s VS ai2 の 対戦結果 の表です。× を担当 する場合の 成績 が 若干悪くなっています が、成績 は ほぼ同じ です。

関数名	o 勝	o 負	o 分	x 勝	x 負	x 分	勝	負	分
ai10s	97.4	0.0	2.6	85.6	2.6	11.7	91.5	1.3	7.2
ai11s	98.1	0.0	1.9	82.5	1.9	15.6	90.3	1.0	8.7

次に、ai10s と 対戦 を行います。

ai_match(ai=[ai10s, ai9s])

実行結果（実行結果はランダムなので下記とは異なる場合があります）

ai11s VS ai10s
count     win    lose    draw
o        2186       0    7814
x           0    5014    4986
total    2186    5014   12800

ratio     win    lose    draw
o       21.9%    0.0%   78.1%
x        0.0%   50.1%   49.9%
total   10.9%   25.1%   64.0%

実行結果 の 通算成績 から、ai11s が ai10s に 対して 弱くなってしまう ことが 確認 できました。何故このようになってしまったかにつては、次回の記事で説明することにします。

今回の記事のまとめ

今回の記事では、強い AI の ルール を作るための 条件の種類 として、必要条件、十分条件、その どちらでもない条件 について 説明 しました。

また、複数の条件 を 同時に考慮 する 評価値 の 計算方法 について 説明 しました。評価値 を 利用 することで、以前の記事で説明した、複数の条件 を 組み合わせて考慮 したい場合の 問題点 を 解決 することが できます。

本記事で入力したプログラム

以下のリンクから、本記事で入力して実行した JupyterLab のファイルを見ることができます。

以下のリンクは、今回の記事で更新した marubatsu.py です。

以下のリンクは、今回の記事で更新した ai.py です。

次回の記事

1. たとえば、1000 年後の世界を自分の目で見る いう 目的 に対する 必要十分条件 は「1000年後まで生きる」ですが、その 条件 を 達成 することは現実的には 不可能 でしょう。なお、必要条件 の一つは「10 年以上生きる」、十分条件 の一つは「1100年 後まで生きる」です ↩

2. 既に ルール 8 が分かりづらいと思っている方はいませんか？ ↩

3. その際に、次の条件 を 考える ために、強くならなかった理由 を 考察する と良いでしょう ↩