Pythonで〇×ゲームのAIを一から作成する　その49　評価値の計算方法

Last updated at 2024-02-01Posted at 2024-01-28

目次と前回の記事

これまでに作成したモジュール

以下のリンクから、これまでに作成したモジュールを見ることができます。

これまでに作成した AI

これまでに作成した AI のアルゴリズムは以下の通りです。

関数名	アルゴリズム
`ai1`	左上から順に空いているマスを探し、最初に見つかったマスに着手する
`ai2` `ai2s`	ランダムなマスに着手する
`ai3` `ai3s`	真ん中のマスに優先的に着手する既に埋まっていた場合はランダムなマスに着手する
`ai4`	真ん中、隅のマスの順で優先的に着手する既に埋まっていた場合はランダムなマスに着手する
`ai5`	勝てる場合に勝つそうでない場合はランダムなマスに着手する
`ai6`	勝てる場合に勝つそうでない場合は相手の勝利を阻止するそうでない場合はランダムなマスに着手する
`ai7`	真ん中のマスに優先的に着手するそうでない場合は勝てる場合に勝つそうでない場合は相手の勝利を阻止するそうでない場合はランダムなマスに着手する

基準となる ai2 との 対戦結果（単位は %）は以下の通りです。太字は ai2 VS ai2 よりも 成績が良い 数値を表します。欠陥の列は、アルゴリズム に欠陥があるため、ai2 との 対戦成績 が 良くても強い とは 限らない ことを表します。欠陥の詳細については、関数名のリンク先の説明を見て下さい。

関数名	o 勝	o 負	o 分	x 勝	x 負	x 分	勝	負	分	欠陥
`ai1`	78.1	17.5	4.4	44.7	51.6	3.8	61.4	34.5	4.1	あり
`ai2`	58.7	28.8	12.6	29.1	58.6	12.3	43.9	43.7	12.5
`ai3`	69.3	19.2	11.5	38.9	47.6	13.5	54.1	33.4	12.5
`ai4`	83.0	9.5	7.4	57.2	33.0	9.7	70.1	21.3	8.6	あり
`ai5`	81.2	12.3	6.5	51.8	39.8	8.4	66.5	26.0	7.4
`ai6`	88.9	2.2	8.9	70.3	6.2	23.5	79.6	4.2	16.2
`ai7`	95.8	0.2	4.0	82.3	2.4	15.3	89.0	1.3	9.7

評価値を利用したルール 1 で着手を行う AI の定義

前回の記事では、評価値を利用 した アルゴリズム で ルール 2、3 で着手を行う AI を定義 しました。今回記事では、ルール 1、4 で着手を行う AI を定義 する事にします。

まず、下記の ルール 1 で着手を行う ai1s を定義します。

左上から順 に 空いているマス を探し、最初に見つかったマス に着手する

このルールに従って、評価値をどのように計算するかについて少し考えてみて下さい。

このルールは、下記のようなルールに 置き換える ことができます。

(0, 0) のマスが空いていればそこに着手する
(1, 0) のマスが空いていればそこに着手する
(2, 0) のマスが空いていればそこに着手する
(0, 1) のマスが空いていればそこに着手する
(1, 1) のマスが空いていればそこに着手する
(2, 1) のマスが空いていればそこに着手する
(0, 2) のマスが空いていればそこに着手する
(1, 2) のマスが空いていればそこに着手する
(2, 2) のマスが空いていればそこに着手する

従って、評価値を利用 した アルゴリズム の場合は、上記の条件のうち、上に記述 されているマスに 着手した局面 の 評価値 が、下に記述 されているマスに 着手した局面 の 評価値より も 大きくなる ように、それぞれのマスの 評価値を設定 すればよいことが分かります。

一例として、下図のように 評価値を設定 することができます。本記事では下図の評価値を採用しますが、上記の条件が満たされていれば、他の評価値 を設定しても かまいません。

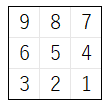
本記事では、上記の評価値 を計算する ai1s の 評価関数 を定義する いくつかの方法 を紹介します。どのように定義すればよいかについて少し考えてみて下さい。

なお、マスの座標から 評価値 を計算する処理は、以前の記事で紹介した 数値座標 を xy 座標 に変換する処理の逆なので、忘れた方は、そちらを復習して下さい。

`ai1s` の定義その 1（if 文を使う方法）

下記は、if 文 を使ってそれぞれの座標に対する 評価値 を計算する ai1s のプログラムです。初心者でも思いつくことができる方法だと思いますので、説明は省略します。

from ai import ai_by_score

def ai1s(mb, debug=False):
    def eval_func(mb):
        if mb.last_move == (0, 0):
            return 9
        elif mb.last_move == (1, 0):
            return 8
        elif mb.last_move == (2, 0):
            return 7
        elif mb.last_move == (0, 1):
            return 6
        elif mb.last_move == (1, 1):
            return 5
        elif mb.last_move == (2, 1):
            return 4
        elif mb.last_move == (0, 2):
            return 3
        elif mb.last_move == (1, 2):
            return 2
        elif mb.last_move == (2, 2):
            return 1

    return ai_by_score(mb, eval_func, debug=debug)

動作の確認

ai1s が 正しく動作 するかどうかを確認するために、ai1 と対戦を行います。以前の記事で説明したように、ai1 VS ai1 では、ai1 の アルゴリズム には ランダム性はない ので、10000 回の すべての対戦 で 〇が勝利 します。実行結果 から、ai1s を 正しく実装 できていることが確認できました。

from ai import ai_match, ai1, ai4

ai_match(ai=[ai1s, ai1])

実行結果

ai1s VS ai1
count     win    lose    draw
o       10000       0       0
x           0   10000       0
total   10000   10000       0

ratio     win    lose    draw
o      100.0%    0.0%    0.0%
x        0.0%  100.0%    0.0%
total   50.0%   50.0%    0.0%

`ai1s` の定義その 2（list によるテーブルを使う方法）

以前の記事で、Excel 座標 から xy 座標 への 対応づけ を、excel_to_xy_table という dict を使った テーブル（表）で行いました。それと 同様の方法 で、マスの座標 とそのマスに着手した場合の 評価値 を 対応づける ことができます。ただし、その方法を利用するためには、dict のキーに利用できる データの種類 を理解する必要があります。

ハッシュ可能なオブジェクトとハッシュ値

これまでのプログラムでは、dict のキーには、主に 文字列型 のデータを利用してきましたが、dict のキーには ハッシュ可能なオブジェクト（hashable）を利用することができます。ハッシュ可能なオブジェクト とは、以下の性質を持つ オブジェクト です。

その オブジェクト が存在している間は、決して 変更されることがない、ハッシュ値（hash value）と呼ばれる 整数型 の データ を持つ
ハッシュ可能なオブジェクトどうし を == 演算子で 等しいか どうかを比較することができ、== の 判定結果 が True になる場合は、必ず 同じハッシュ値 を持つ

細かい話になりますが、誤解されがち な点についていくつか補足します。ただし、下記の補足は、ハッシュ値 を 直接扱う ようなプログラムを記述する 場合でなければ、気にする必要 は ありません。

ハッシュ可能なオブジェクト は 必ず == 演算子で比較することができますが、ハッシュ可能 でない オブジェクトを == 演算子で 比較できるか どうかは、その オブジェクトの種類 によって 異なります。例えば list や dict はハッシュ可能 でない オブジェクトですが、== 演算子で比較することが できます。

上記の 2 つ目 の性質の逆の、「同じハッシュ値 を持つ オブジェクト は、== の 判定結果 が True になる」は必ずしも 正しい とは 限りません。同じハッシュ値 を持つ オブジェクト が 等しくない と判定される事を ハッシュ値の衝突 と呼びます。

ハッシュ可能なオブジェクト の詳細については、下記のリンク先を参照して下さい。

dict のキーにハッシュ可能なオブジェクトのみが利用できる理由

dict のキーに ハッシュ可能なオブジェクトのみ が利用できる理由は、dict は、キーの値 を、キーの ハッシュ値 を利用して管理しているからです。具体的な仕組については説明が長くなるので省略しますが、簡単にいうと、下記の理由から、ハッシュ値 を利用することで、効率よく dict のキーと キーの値 を管理することが できるようになる からです。

キーを指定して、dict から その キーの値 を 取り出す処理 を行う際には、dict に登録されているキーの中から、指定したキー と 等しいキー を 探す必要 がある
ハッシュ値 を利用することで、ハッシュ可能なオブジェクトどうし が 等しいか どうかを 効率的に判定 することができる

逆に言うと、dict のキーにハッシュ可能 でない オブジェクトを 利用できる ように してしまう と、dict の処理が かなり遅く なってしまいます。

ハッシュ という概念は、コンピューター に関する技術の中で、かなり 重要な概念 なので、興味がある方は調べてみると良いでしょう。例えば、SNS などで良く使われている ハッシュタグ のハッシュと、ハッシュ値 のハッシュは、同じ概念 の用語です。本記事でも、直接ハッシュ値を扱う機会があれば詳しく解説しようと思います。

参考までに、wikipedia のハッシュのリンクを下記に示します。

ハッシュ可能なオブジェクトの種類

Python の主な ハッシュ可能なオブジェクト は以下の通りです。

数値型、文字列型、論理型、None 型 などの、単一のデータ を扱う、単一データ型 の イミュータブル な オブジェクト
Python の 任意のデータ型 を、複数組み合わせ てデータを表現する 複合データ型 のうち、そのデータ型 および、すべての要素 が イミュータブル な オブジェクト
自分で定義 した クラス の インスタンス

上記の 1 と 2 は、以前の記事で説明した、疑似的な複製 を行うことができるデータです。

上記の 3 は 疑似的な複製 を行うことが できない 場合がありますが、自分で定義 した クラス の インスタンス は、インスタンス が扱うデータの 内容に関わらず、インスタンスごと に 異なるハッシュ値 が 計算される と考えて下さい¹。

従って、〇×ゲーム の 合法手 を表す (1, 2) という tuple は、それ自身 と すべての要素 が ハッシュ可能なオブジェクト なので、ハッシュ可能なオブジェクト に分類されます。

ハッシュ値の取得方法

以前の記事で説明した組み込み関数 id と同様に、一般的 なプログラムで hash を使って ハッシュ値を計算 する必要がある場面はあまり 多くないと 思いますので、興味がない方は、ハッシュ値に関する以下の説明は読み飛ばしても構いません。

オブジェクト の ハッシュ値 は、組み込み関数 hash の 実引数 に オブジェクトを記述 して呼び出すことで 取得する ことができます。また、hash の 実引数 にハッシュ可能 でない オブジェクトを記述して呼び出すと エラーが発生 します。

組み込み関数 hash についての詳細は、下記のリンク先を参照して下さい。

下記のプログラムは、いくつか の データ型 の ハッシュ値 を表示しています。

from marubatsu import Marubatsu
mb = Marubatsu()
print(hash(1))                 # 数値型のデータ
print(hash("abc"))             # 文字列型のデータ
print(hash(True))              # 論理型のデータ
print(hash(None))              # None 型のデータ
print(hash((1, "abc", True)))  # すべての要素がハッシュ可能な tuple
print(hash(mb))                # Marubatsu クラスのインスタンス（この値は毎回異なる）

実行結果

1
5133467580067694764
1
8795299436207
3819214611466916399
145277155213

list は ミュータブル なので、ハッシュ可能なオブジェクト では ありません。従って hash の 実引数に記述 して呼び出すと、下記のプログラムのように エラーが発生 します。

print(hash([1, 2, 3]))

実行結果

---------------------------------------------------------------------------
TypeError                                 Traceback (most recent call last)
Cell In[4], line 1
----> 1 print(hash([1, 2, 3]))

TypeError: unhashable type: 'list'

上記のエラーメッセージは、以下のような意味を持ちます。

TypeError
データ型（type）に関するエラー
unhashable type: 'list'
list はハッシュ可能でない（unhashable）データ型（type）である

tuple は イミュータブル なデータですが、その要素に ミュータブル なデータが 含まれている 場合も、下記のプログラムのように エラーが発生 します。

print(hash((1, [2, 3])))  # 要素にミュータブルな list が含まれている

実行結果

---------------------------------------------------------------------------
TypeError                                 Traceback (most recent call last)
Cell In[5], line 1
----> 1 print(hash((1, [2, 3])))

TypeError: unhashable type: 'list'

ハッシュ値の性質

この説明も 当面は利用 しない知識なので、興味がない方は読み飛ばしてもかまいません。

Python の、ハッシュ可能 な 組み込み型 のデータは、同じ内容 であれば、常に 同じハッシュ値 を持ちます。例えば、下記のプログラムの a と b には 同一の要素の値 を持つ tuple が代入されています。a と b は 異なるオブジェクト なので、下記のプログラムのように、id を表示すると 異なる値 が表示されますが、ハッシュ値 は同一になります。

a = (1, 2)
b = (1, 2)
print(id(a))
print(id(b))
print(hash(a))
print(hash(b))

実行結果（異なる数値が表示される場合があります）

2324448500864
2324448507456
-3550055125485641917
-3550055125485641917

自分で定義 した クラス の インスタンス の場合は、基本的¹には作成した インスタンスごと に 異なるハッシュ値 が表示されます。下記のプログラムは、Marubastu クラスの 2 つの インスタンス の ハッシュ値 を表示していますが、どちらもゲーム開始直後 を 表します が、異なるインスタンス に 異なるハッシュ値 が付けられていることがわかります。

mb1 = Marubatsu()
mb2 = Marubatsu()
print(hash(mb1))
print(hash(mb2))

実行結果（異なる値が表示される場合があります）

145278027657
145277956725

テーブルを使った `ai1s` の定義

ゲーム盤の座標 を表す tuple をキーとし、その キーの値 に キーの座標 に着手した局面の 評価値 を代入することで、ai1s を下記のプログラムのように定義できます。なお、先程の ai1s と修正点が多すぎるので、修正箇所は省略します。

3 ~ 7 行目：座標から 評価値 を対応づける テーブル を表す dict のデータを記述し、ローカル変数 score_table に代入する
8 行目：テーブルから 着手した座標の 評価値 を求めて 返り値 として返す

 1  def ai1s(mb, debug=False):
 2      def eval_func(mb):
 3          score_table = {
 4              (0, 0): 9, (1, 0): 8, (2, 0): 7,
 5              (0, 1): 6, (1, 1): 5, (2, 1): 4,
 6              (0, 2): 3, (1, 2): 2, (2, 2): 1,
 7          }
 8          return score_table[mb.last_move]
 9
10    return ai_by_score(mb, eval_func, debug=debug)

行番号のないプログラム

def ai1s(mb, debug=False):
    def eval_func(mb):
        score_table = {
            (0, 0): 9, (1, 0): 8, (2, 0): 7,
            (0, 1): 6, (1, 1): 5, (2, 1): 4,
            (0, 2): 3, (1, 2): 2, (2, 2): 1,
        }
        return score_table[mb.last_move]

    return ai_by_score(mb, eval_func, debug=debug)

動作の確認

ai1s が 正しく動作 するかどうかを確認するために、ai1 と対戦を行います。実行結果 から、ai1s を 正しく実装 できていることが確認できました。

ai_match(ai=[ai1s, ai1])

実行結果

ai1s VS ai1
count     win    lose    draw
o       10000       0       0
x           0   10000       0
total   10000   10000       0

ratio     win    lose    draw
o      100.0%    0.0%    0.0%
x        0.0%  100.0%    0.0%
total   50.0%   50.0%    0.0%

`ai1s` の定義その 3（式で計算する方法）

評価値 を、下図のように、規則正しく設定 した場合は、式を使って 評価値 を計算することが できます。どのような式を記述すればよいかについて少し考えてみて下さい。

以前の記事で、下図のマスの 数値座標 から、xy 座標 を計算する式を紹介しました。

具体的には、実引数 に、上図のマスの 数値座標 を記述して呼び出すと、xy 座標 を表す tuple を 返り値 として返す num_to_xy を下記のプログラムのように定義しました。

def num_to_xy(coord):
    x = coord % 3
    y = coord // 3
    return x, y

一旦 評価値 の事を 忘れて、上記の関数 の 逆の処理、すなわち xy 座標 から 数値座標 を計算する処理を行うプログラムを考えることにします。上図から、数値座標 は、x 座標 が 1 増える と 1 増える ことが分かります。また、y 座標 が 1 増える と 3 増える ことが分かります。従って、xy 座標 から 数値座標 を計算する式は、下記のように記述できます。

coord = x * 1 + y * 3

x * 1 は x と同じなので、上記の式は下記のように記述できます。

coord = x + y * 3

次に、下記の 評価値 の図と、数値座標 の図を 並べて みて、それぞれ の 同じ座標 の マスの数字 に どのような関係 が あるか について考えてみて下さい。

よく見れば、同じ座標 の マスの数値 を合計するといずれも 9 になる ことが分かります。従って、評価値 と 数値座標 の関係には、下記の等式 が 成り立ち ます。

$数値座標 + 評価値 = 9$

この等式を変形すると、以下のようになります。

$評価値 = 9 - 数値座標$

従って、評価値 を score という変数で表すと、評価値 は 下記の式 で計算できます。

score = 9 - (x + y * 3)

上記から、ai1s は下記のプログラムのように定義できます。なお、先程の ai1s と修正点が多すぎるので、修正箇所は省略します。このように、評価値 を 規則正しい値 に設定することで 簡単な式 で 評価値 を 計算できる場合 があります。

3 行目：着手した座標から、x 座標 と y 座標 を 取り出し て x と y に代入する
4 行目：先ほどの式 を使って、座標から 評価値 を計算し、その値を返す

1  def ai1s(mb, debug=False):
2      def eval_func(mb):
3          x, y = mb.last_move
4          return 9 - (x + y * 3)
5
6      return ai_by_score(mb, eval_func, debug=debug)

行番号のないプログラム

def ai1s(mb, debug=False):
    def eval_func(mb):
        x, y = mb.last_move
        return 9 - (x + y * 3)

    return ai_by_score(mb, eval_func, debug=debug)

デバッグ表示による動作の確認

今回は、念のため に本当に 正しく実装 できているかどうかを、下記のプログラムで、デバッグ表示 を行うことで確認することにします。実行結果 の score の表示から、左上のマス から 9、8、・・・、1 の順で、正しい評価値 が計算されることが確認できます。

from marubatsu import Marubatsu

mb = Marubatsu()
ai1s(mb, debug=True)

実行結果

Start ai_by_score
Turn o
...
...
...

legal_moves [(0, 0), (1, 0), (2, 0), (0, 1), (1, 1), (2, 1), (0, 2), (1, 2), (2, 2)]
====================
move (0, 0)
Turn x
O..
...
...

score 9 best score -inf
UPDATE
  best score 9
  best moves [(0, 0)]
====================
move (1, 0)
Turn x
.O.
...
...

score 8 best score 9
====================
move (2, 0)
Turn x
..O
...
...

score 7 best score 9
====================
move (0, 1)
Turn x
...
O..
...

score 6 best score 9
====================
move (1, 1)
Turn x
...
.O.
...

score 5 best score 9
====================
move (2, 1)
Turn x
...
..O
...

score 4 best score 9
====================
move (0, 2)
Turn x
...
...
O..

score 3 best score 9
====================
move (1, 2)
Turn x
...
...
.O.

score 2 best score 9
====================
move (2, 2)
Turn x
...
...
..O

score 1 best score 9
====================
Finished
best score 9
best moves [(0, 0)]

対戦による動作の確認

ai_match(ai=[ai1s, ai1])

実行結果

ai1s VS ai1
count     win    lose    draw
o       10000       0       0
x           0   10000       0
total   10000   10000       0

ratio     win    lose    draw
o      100.0%    0.0%    0.0%
x        0.0%  100.0%    0.0%
total   50.0%   50.0%    0.0%

`ai1s` の定義その 4（最初の最善手を採用する）

下記の ルール 1 には ランダム性 は ありません。

左上から順 に 空いているマス を探し、最初に見つかったマス に着手する

このような場合は、前回の記事のノートで説明したように、評価値を利用 した アルゴリズム の 手順 2 を「最も高い評価値 がつけられたものが 複数ある場合 は、最初にみつかったもの を選択」にした アルゴリズム を利用することが できます。

具体的には、下記のような アルゴリズム で処理を行います。

これまで の ai1s と 異なり、すべての着手 の 評価値 を 同じ値 にする
ai_by_score で計算した 最も高い評価値 の 合法手の一覧 を表す best_moves の、先頭の要素 の 合法手 を採用する

評価値 は、すべて同じ であれば どのような値 でも 構わない ので、0 を設定します。

次に、ai_by_score が best_moves の中から ランダムな合法手 を選択するか、先頭の合法手 を選択するかを、選べるように改良 する必要があります。

`ai_by_score` の改良

具体的には、下記のプログラムのように、ai_by_score を修正します。

5 行目：最善手の一覧 の中から ランダム な着手を 選ぶか どうかを表す仮引数 rand を追加する。この仮引数を、デフォルト値 が True の デフォルト引数 とすることで、これまでに作成した AI を 変更しなくても良い ようにした
6、7 行目：rand が True の場合は これまで通り、ランダム な合法手を 選択して返す 処理を行う
8、9 行目：rand が False の場合は、先頭の合法手 を表す 0 番の要素 を返す

仮引数の名前 を random にしなかったのは、random という名前の本記事でも利用している、良く使われる モジュールがある からです。

1  from copy import deepcopy
2  from random import choice
3  from ai import dprint
4
5  def ai_by_score(mb_orig, eval_func, debug=False, rand=True):
元と同じなので省略
6      if rand:   
7          return choice(best_moves)
8      else:
9          return best_moves[0]

行番号のないプログラム

from copy import deepcopy
from random import choice
from ai import dprint

def ai_by_score(mb_orig, eval_func, debug=False, rand=True):
    dprint(debug, "Start ai_by_score")
    dprint(debug, mb_orig)
    legal_moves = mb_orig.calc_legal_moves()
    dprint(debug, "legal_moves", legal_moves)
    best_score = float("-inf")
    best_moves = []
    for move in legal_moves:
        dprint(debug, "=" * 20)
        dprint(debug, "move", move)
        mb = deepcopy(mb_orig)
        x, y = move
        mb.move(x, y)
        dprint(debug, mb)
        
        score = eval_func(mb)
        dprint(debug, "score", score, "best score", best_score)
        
        if best_score < score:
            best_score = score
            best_moves = [move]
            dprint(debug, "UPDATE")
            dprint(debug, "  best score", best_score)
            dprint(debug, "  best moves", best_moves)
        elif best_score == score:
            best_moves.append(move)
            dprint(debug, "APPEND")
            dprint(debug, "  best moves", best_moves)

    dprint(debug, "=" * 20)
    dprint(debug, "Finished")
    dprint(debug, "best score", best_score)
    dprint(debug, "best moves", best_moves)
    if rand:   
        return choice(best_moves)
    else:
        return best_moves[0]

修正箇所

from copy import deepcopy
from random import choice
from ai import dprint

def ai_by_score(mb_orig, eval_func, debug=False, random=True):
元と同じなので省略
    if rand:   
        return choice(best_moves)
    else:
        return best_moves[0]

`ai1s` の修正

次に、ai1s を下記のプログラムのように修正します。

3 行目：評価値 は 常に 0 を返すようにする
5 行目：キーワード引数 rand=False を記述することで、ai_by_score が 先頭の合法手 を返すようにする

def ai1s(mb, debug=False):
    def eval_func(mb):
        return 0

    return ai_by_score(mb, eval_func, debug=debug, rand=False)

動作の確認

ai_match(ai=[ai1s, ai1])

実行結果

ai1s VS ai1
count     win    lose    draw
o       10000       0       0
x           0   10000       0
total   10000   10000       0

ratio     win    lose    draw
o      100.0%    0.0%    0.0%
x        0.0%  100.0%    0.0%
total   50.0%   50.0%    0.0%

仮引数 `rand` の処理の確認

rand=False が 正しく動作するか どうかが心配な方は、下記のプログラムのように、ai1s の ai_by_score の 実引数 から、rand=False を削除した、ai1s_buggy を定義して、ai1 と対戦 すると良いでしょう。実行結果 から、通算成績 の勝率と敗率が 異なる ので、rand=False によって ai_by_score の処理が 正しく切り替わる ことが確認できます。

def ai1s_buggy(mb, debug=False):
    def eval_func(mb):
        return 0

    return ai_by_score(mb, eval_func, debug=debug)

ai_match(ai=[ai1s_buggy, ai1])

実行結果（実行結果はランダムなので下記とは異なる場合があります）

ai1s_buggy VS ai1
count     win    lose    draw
o        5151    4455     394
x        1748    7825     427
total    6899   12280     821

ratio     win    lose    draw
o       51.5%   44.5%    3.9%
x       17.5%   78.2%    4.3%
total   34.5%   61.4%    4.1%

評価値を利用したルール 4 で着手を行う AI の定義

次は、下記の、ルール 4 で着手を行う AI を定義 します。

真ん中、隅のマスの順で 優先的 に着手する
既に 埋まっていた場合 は ランダム なマスに着手する

評価値の設定

ルール 4 は、(1, 1)、(0, 0)、(2, 0)、(0, 2)、(2, 2) の順番で 優先的 に着手を行います。ルール 1 の場合と 同様の方法 でそれらのマスの 評価値 を 設定する ことにした場合、それぞれ のマスに着手した局面の 評価値 は 5、4、3、2、1 になります。

上記以外 のマスしか 残っていない 場合は、ランダムな着手 を行うので、それらの 評価値 は、上記の場合 の どの評価値 よりも低い、1 未満 の 同じ値 に設定すればよいことが分ります。そこで、その 評価値 を 0 にすることにします。

下図は、上記に従って、それぞれのマス に着手した場合の局面の 評価値 です。

`ai4s` の定義の方法

この 評価値 を計算する ai4s の定義として、先程と同様 に if 文 を使う方法と、テーブル を使う方法が考えられますが、どちらも プログラムの 記述がかなり面倒 です。なお、どちらも面倒ではありますが、特に難しい点はない のでプログラムの 記述は省略 します。興味と時間に余裕ががある方は実際に記述してみて下さい。また、ルール 4 は ランダム性がある ので 先程実装 した ai_by_score の rand=False の処理を利用することは できません。

そこで本記事では、計算を使って ai4s を実装する方法について説明します。

真ん中、四隅、それ以外 のマスを 分けて処理 する必要があるので、その部分 は if 文 で記述する必要があります。そのため、ai4s を下記のプログラムのように記述します。

3、4 行目：真ん中 のマスに着手していた場合は 5 を返す
5、6 行目：四隅のマスに着手していた場合は、その 評価値 を 式で計算 して返す
7、8 行目：それ以外 の場合は 0 を返す

下記の 5、6 行目の、日本語で記述 されている部分に、どのようなプログラムを記述す場良いかについて少し考えてみて下さい。

 1  def ai4s(mb, debug=False):
 2      def eval_func(mb):
 3          if mb.last_move == (1, 1):
 4              return 5
 5          elif 四隅のマスの場合:
 6              return 四隅の場合の評価値を計算する式
 7          else:
 8             return 0
 9
10      return ai_by_score(mb, eval_func, debug=debug)

四隅のマスであることの判定方法

単純に 考える のであれば、下記のような 条件式 を記述すれば良いのですが、このプログラムは長いので、入力が大変、入力ミス の 可能性が高くなる などの欠点があります。

elif mb.last_move == (0, 0) or mb.last_move == (2, 0) or \
     mb.last_move == (0, 2) or mb.last_move == (2, 2):

このような場合は、四隅のマス の座標と、それ以外 のマスの座標を下記の表のように並べ、四隅のマスに あって 、それ以外 のマスにない、特長を探す と良いでしょう。なお、真ん中 のマスは最初に 判定済 なので考慮する必要は ありません。

位置	座標
四隅	(0, 0)、(2, 0)、(0, 2)、(2, 2)
それ以外	(1, 0)、(0, 1)、(2, 1)、(1, 2)

上記をよく見ると、以下の性質 があることが分かります。

四隅の x、y 座標 は、いずれも 0 または 2 である
それ以外 の x、y 座標 は 上記の性質 を 満たさない

四隅を判定する式の記述方法

従って、この性質を利用することで、ai4s を下記のプログラムのように記述できます。

3 行目：着手した座標から、x 座標 と y 座標 を 取り出し て x と y に代入する
6 行目：x 座標 と y 座標 が いずれも 0 または 2 であることを判定する。or 演算子 は and 演算子より も 優先順位が低い ので、( と ) で 囲う必要がある 点に注意すること

 1  def ai4s(mb, debug=False):
 2      def eval_func(mb):
 3          x, y = mb.last_move
 4          if mb.last_move == (1, 1):
 5              return 5
 6          elif (x == 0 or x == 2) and (y == 0 or y == 2):
 7              return 四隅の場合の評価値を計算する式
 8          else:
 9              return 0
10
11      return ai_by_score(mb, eval_func, debug=debug)

修正箇所

def ai4s(mb, debug=False):
    def eval_func(mb):
+       x, y = mb.last_move
        if mb.last_move == (1, 1):
            return 5
-       elif 四隅のマスの場合:
+       elif (x == 0 or x == 2) and (y == 0 or y == 2):
            return 四隅の場合の評価値を計算する式
        else:
            return 0

    return ai_by_score(mb, eval_func, debug=debug)

四隅を判定する式の別の記述方法

数字に 慣れた 方は、上記の性質 を 一般化 した 下記の性質 を 思いつく かもしれません。

四隅の x、y 座標 は、いずれも偶数 である
それ以外 の x、y 座標 は 上記の性質 を 満たさない

整数が偶数で あるか どうかは、2 で 割った余り が 0 であるか どうかで判定できます。また、Python では % という 演算子 を使って、割り算 の余りを計算することができます。従って、ai4s は、下記のプログラムのように、より 簡潔に記述 できます。

6 行目：余りを計算 することで x 座標 と y 座標 が いずれも偶数 であることを判定する

def ai4s(mb, debug=False):
    def eval_func(mb):
        x, y = mb.last_move
        if mb.last_move == (1, 1):
            return 5
        elif x % 2 == 0 and y % 2 == 0:
            return 四隅の場合の評価値を計算する式
        else:
            return 0

    return ai_by_score(mb, eval_func, debug=debug)

修正箇所

def ai4s(mb, debug=False):
    def eval_func(mb):
        x, y = mb.last_move
        if mb.last_move == (1, 1):
            return 5
-       elif (x == 0 or x == 2) and (y == 0 or y == 2):
+       elif x % 2 == 0 and y % 2 == 0:
            return 四隅の場合の評価値を計算する式
        else:
            return 0

    return ai_by_score(mb, eval_func, debug=debug)

四隅のマスの評価値の計算

下図の四隅のマスに着手した局面の 評価値 を 式で計算 するためには、x と y を 使った式 で、下記の表 のような 評価値 を計算する式を考える必要があります。

x	y	評価値
`0`	`0`	`4`
`2`	`0`	`3`
`0`	`2`	`2`
`2`	`2`	`1`

式を考える ために、x と y と 評価値 の関係を下記のように考察します。

x と y が 共に 0 の場合の 評価値 は 4 である
x が 2 増える と、評価値 は 1 減る
y が 2 増える と、評価値 は 2 減る

従って、評価値 は 下記の式 で計算できることが分かります。実際に、上記の表の x、y の値をこの 式に代入 して 正しい評価値 が計算できるかどうかを確認して下さい。

score = 4 - (x / 2 + y)

`ai4s` の定義と動作の確認

この式 を ai4s に 当てはめる と、下記のプログラムの 7 行目 のようになります。

 1  def ai4s(mb, debug=False):
 2      def eval_func(mb):
 3          x, y = mb.last_move
 4          if mb.last_move == (1, 1):
 5              return 5
 6          elif x % 2 == 0 and y % 2 == 0:
 7              return 4 - (x / 2 + y)
 8          else:
 9              return 0
10
11      return ai_by_score(mb, eval_func, debug=debug)

行番号のないプログラム

def ai4s(mb, debug=False):
    def eval_func(mb):
        x, y = mb.last_move
        if mb.last_move == (1, 1):
            return 5
        elif x % 2 == 0 and y % 2 == 0:
            return 4 - (x / 2 + y)
        else:
            return 0

    return ai_by_score(mb, eval_func, debug=debug)

修正箇所

def ai4s(mb, debug=False):
    def eval_func(mb):
        x, y = mb.last_move
        if mb.last_move == (1, 1):
            return 5
        elif x % 2 == 0 and y % 2 == 0:
-           return 四隅の場合の評価値を計算する式
+           return 4 - (x / 2 + y)
        else:
            return 0

    return ai_by_score(mb, eval_func, debug=debug)

ai4s が 正しく動作 するかどうかを確認するために、ai4 と対戦を行います。実行結果 から、ai4s を 正しく実装 できていることが確認できました。

ai_match(ai=[ai4s, ai4])

実行結果（実行結果はランダムなので下記とは異なる場合があります）

ai4s VS ai4
count     win    lose    draw
o        2520    4099    3381
x        4127    2404    3469
total    6647    6503    6850

ratio     win    lose    draw
o       25.2%   41.0%   33.8%
x       41.3%   24.0%   34.7%
total   33.2%   32.5%   34.2%

別の実装方法

上記で、四隅に着手 した際の 評価値 を 改めて考える のが面倒だと思った方はいませんか？実は、四隅の 評価値 は、ルール 1 と 同じ式 で計算することが できます。

その理由は、評価値を利用 する アルゴリズム では、「優先したいもの の 評価値 が、それより も 優先したくないもの の 評価値 よりも 大きくなる」ような 評価値 であれば、それぞれ に どのような評価値 を設定しても 構わない からです。具体的には、四隅の 評価値 を 下図左 のように、下図右 の ルール 1 の 評価値 と 同じ値 に設定しても構いません。

`ai4s` の定義と動作の確認

従って、四隅の 評価値 を計算する 式__は、ルール 1 の評価値を計算する式と同じ式を利用することができるので、ai4s__ は、下記のプログラムのように記述できます。

7 行目：四隅のマスの 評価値 の 計算式 を ai1s と同じものにする

 1  def ai4s(mb, debug=False):
 2      def eval_func(mb):
 3          x, y = mb.last_move
 4          if mb.last_move == (1, 1):
 5              return 5
 6          elif x % 2 == 0 and y % 2 == 0:
 7              return 9 - (x + y * 3)
 8          else:
 9              return 0
10
11      return ai_by_score(mb, eval_func, debug=debug)

行番号のないプログラム

def ai4s(mb, debug=False):
    def eval_func(mb):
        x, y = mb.last_move
        if mb.last_move == (1, 1):
            return 5
        elif x % 2 == 0 and y % 2 == 0:
            return 9 - (x + y * 3)
        else:
            return 0

    return ai_by_score(mb, eval_func, debug=debug)

修正箇所

def ai4s(mb, debug=False):
    def eval_func(mb):
        x, y = mb.last_move
        if mb.last_move == (1, 1):
            return 5
        elif x % 2 == 0 and y % 2 == 0:
-           return 4 - (x / 2 + y)
+           return 9 - (x + y * 3)
        else:
            return 0

    return ai_by_score(mb, eval_func, debug=debug)

ai4s が 正しく動作 するかどうかを確認するために、ai4 と対戦を行います。実行結果 から、通算成績 の勝率と敗率が 異なる ので、ai4s を正しく実装 できていない ことが確認できました。どこに問題があるか について少し考えてみて下さい。

ai_match(ai=[ai4s, ai4])

実行結果（実行結果はランダムなので下記とは異なる場合があります）

ai4s VS ai4
count     win    lose    draw
o        6616    1698    1686
x        4167    2495    3338
total   10783    4193    5024

ratio     win    lose    draw
o       66.2%   17.0%   16.9%
x       41.7%   24.9%   33.4%
total   53.9%   21.0%   25.1%

バグの原因

バグの原因 は、真ん中 のマスに着手した場合の 評価値 が 5 のまま だからです。そのため、上記の ai4s では、真ん中 のマスの (1, 1) の 5 より 評価値が高い、(0, 0) と (2, 0) が 優先的 に着手されてしまいます。このように、評価値を利用 する アルゴリズム では、評価値 を 別の値 に修正した際に、他のより 優先したい（または 優先したくない）ものの 評価値 の 大小の関係 が 変化しない ように注意する必要があります。

四隅のマスに着手した際の 評価値 を 先ほど のように修正した場合は、より優先 する 真ん中 の (1, 1) の 評価値 を、四隅の 評価値 の 最大値 である 9 より も 大きな値 に 設定し直す 必要があります。9 より 大きければ どのような値でも 構わない ので 10 を設定することにします。なお、真ん中 と 四隅以外 のマスの 評価値 は 0 のまま で 問題はありません。

下図は、修正後 の 各マス の 評価値 を表します。

評価値 の修正を行う際に、先程のような バグが発生 することを 避ける ためには、上記のような 図を作成 すると良いでしょう。他の方法としては、下記の表のように、優先したい条件 の順番で 評価値 の範囲を 表にしたもの を作製して、優先したいものに 対して、より大きな評価値 が設定されることが 確認できる ようにすると良いでしょう。

条件	評価値の範囲
真ん中のマスに着手	10
四隅のマスに着手	1 ~ 9
それ以外のマスに着手	0

他にも、評価値 を修正した際に、大小の関係 が簡単に 変化しない ように、それぞれ の条件の 評価値の範囲 の間隔を 大きめに設定 するという方法があります。例えば、真ん中 のマスの着手に対する 評価値 に 100 を設定することで、今後、四隅のマスの着手に対する 評価値 を 多少変えた場合 に、間違って 100 より大きくなる可能性 が低くなります。ただし、この方法は決して 完璧ではない ので、過信せず に、評価値 を修正した場合は、必ず 全体の評価値 の 値を確認 することを 強くお勧めします。

`ai4s` の修正と動作の確認

修正した 評価値 を計算する ai4s は、下記のプログラムのように記述できます。

5 行目：(1, 1) のマスの 評価値 を 10 にする

 1  def ai4s(mb, debug=False):
 2      def eval_func(mb):
 3          x, y = mb.last_move
 4          if mb.last_move == (1, 1):
 5              return 10
 6          elif x % 2 == 0 and y % 2 == 0:
 7              return 9 - (x + y * 3)
 8          else:
 9              return 0
10
11      return ai_by_score(mb, eval_func, debug=debug)

行番号のないプログラム

def ai4s(mb, debug=False):
    def eval_func(mb):
        x, y = mb.last_move
        if mb.last_move == (1, 1):
            return 10
        elif x % 2 == 0 and y % 2 == 0:
            return 9 - (x + y * 3)
        else:
            return 0

    return ai_by_score(mb, eval_func, debug=debug)

修正箇所

def ai4s(mb, debug=False):
    def eval_func(mb):
        x, y = mb.last_move
        if mb.last_move == (1, 1):
-           return 10
+           return 5
        elif x % 2 == 0 and y % 2 == 0:
            return 9 - (x + y * 3)
        else:
            return 0

    return ai_by_score(mb, eval_func, debug=debug)

ai_match(ai=[ai4s, ai4])

実行結果（実行結果はランダムなので下記とは異なる場合があります）

ai4s VS ai4
count     win    lose    draw
o        2499    4214    3287
x        4196    2414    3390
total    6695    6628    6677

ratio     win    lose    draw
o       25.0%   42.1%   32.9%
x       42.0%   24.1%   33.9%
total   33.5%   33.1%   33.4%

評価値を利用したアルゴリズムの利点

評価値を利用 した アルゴリズム の利点をいくつか紹介します。他の利点に関しては、その利点を活かした例が出てきた時に説明します。

評価値関数を記述するだけで、AI を定義できる

以前の記事で定義した、評価値を利用 した アルゴリズム の ひな形 となる ai_by_score を定義する事で、評価関数 を定義するだけで、AI の関数 を 定義できる ようになります。

ランダムな選択を行うことができる

以前の記事で説明した、条件を満たす着手が複数ある場合の問題点 を解消することができます。具体的には、最大の 評価値 を持つものが複数あった場合に、その中から ランダムに選択 する処理を行うことができます。

ルールの条件の優先順位を柔軟に変えることができる

以前の記事で説明した、条件を判定する順番に関する問題点 を解消することができます。

例えば、ルール 4 は、真ん中 のマス、隅のマスの 優先順位 で着手を行いますが、その 優先順位 を、隅のマス、真ん中 のマスの 優先順位 に 変える 場合に、「それぞれの条件を 順番に判定 し、最初にみつかった 条件を満たす着手 を選択する」というアルゴリズムでは、下記の ai4 のプログラムを、その下 のプログラムのように、真ん中 と隅の処理を行うプログラムの記述の順番を 入れ替える 必要があります。

略
    # 真ん中のマスの場合の処理
    if mb.board[1][1] == Marubatsu.EMPTY:
        return 1, 1
    # 隅のマスの場合の処理
    for y in range(0, 3, 2):
        for x in range(0, 3, 2):
            if mb.board[x][y] == Marubatsu.EMPTY:
                return x, y
略

修正後のプログラム

略
    # 隅のマスの場合の処理
    for y in range(0, 3, 2):
        for x in range(0, 3, 2):
            if mb.board[x][y] == Marubatsu.EMPTY:
                return x, y
    # 真ん中のマスの場合の処理
    if mb.board[1][1] == Marubatsu.EMPTY:
        return 1, 1
略

一方、評価値を利用 する アルゴリズム の場合は、計算する 評価値 を、下記の表 のように 変える ことで、条件の 優先順位 を 変えるこ とができます。なお、下記の表では四隅の 評価値 を 101 ~ 109 にしましたが、10 より多ければ どのような値にしても構いません。

条件	評価値の範囲
四隅のマスに着手	101 ~ 109
真ん中のマスに着手	10
それ以外のマスに着手	0

上記の評価値 を計算するために必要な ai4s の修正は、下記のプログラムの 7 行目 のように、四隅の 評価値 に 100 を足すだけ で簡単に行えます。ただし、下記のプログラムは、ルール 4 と 異なる処理 を行うので、関数の名前は ai4s_fake²としました。

 1  def ai4s_fake(mb, debug=False):
 2      def eval_func(mb):
 3          x, y = mb.last_move
 4          if mb.last_move == (1, 1):
 5              return 10
 6          elif x % 2 == 0 and y % 2 == 0:
 7              return 9 - (x + y * 3) + 100
 8          else:
 9              return 0
10
11      return ai_by_score(mb, eval_func, debug=debug)

行番号のないプログラム

def ai4s_fake(mb, debug=False):
    def eval_func(mb):
        x, y = mb.last_move
        if mb.last_move == (1, 1):
            return 10
        elif x % 2 == 0 and y % 2 == 0:
            return 9 - (x + y * 3) + 100
        else:
            return 0

    return ai_by_score(mb, eval_func, debug=debug)

修正箇所

-def ai4(mb, debug=False):
+def ai4s_fake(mb, debug=False):
    def eval_func(mb):
        x, y = mb.last_move
        if mb.last_move == (1, 1):
            return 10
        elif x % 2 == 0 and y % 2 == 0:
-           return 9 - (x + y * 3)
+           return 9 - (x + y * 3) + 100
        else:
            return 0

    return ai_by_score(mb, eval_func, debug=debug)

なお、ai4s_fake は、ルール 4 とは 異なる処理 を行うので、ai4 との 対戦は行いません。

評価値を利用したアルゴリズムの欠点

評価値を利用 した アルゴリズム は、良いことしかないように思えるかもしれませんが、以下のような欠点があるので、その点には注意して下さい。

処理に時間がかかる場合がある

評価値を利用 した アルゴリズム は、最大の 評価値 を持つものを 調べる必要 があるので、必ず すべてのデータ の 評価値 を計算する必要があります。一方、「それぞれの条件を順番に判定し、最初にみつかった条件を満たす着手を選択する」アルゴリズムでは、条件を満たす ものが 見つかった時点 で 処理を終える ことができます。そのため、ルールによっては、評価値を利用 した アルゴリズム のほうが、処理に 時間がかかる場合 があります。

例えば、ai1 と ai1s は、同じルール で着手を行う AI ですが、ai1s のほうが処理に 時間がかかります。そのことは下記の 2 つのプログラム を実行することで確認できます。

下記の、ai1 どうし で 10000 回対戦 を行う処理は、筆者のパソコンでは 約 2.5 秒 かかりました。なお、実行結果はこれまでと同じなので省略します。

ai_match(ai=[ai1, ai1])

一方、下記の、ai1s どうし で 10000 回対戦 を行う処理は、筆者のパソコンでは 約 32.7 秒 のように、約 10 倍以上 の時間がかかりました。省略しますが、ai2s、ai3s、ai4s も、対応する AI の 約 10 倍 の 処理時間 がかかります。興味がある方は実行してみて下さい。

ai_match(ai=[ai1s, ai1s])

実は、ai1 と ai1s で 約 10 倍以上 も 処理時間 が 異なる のは、ai1 で行う処理が、特定のマス が 空いているかどうか を 調べている のに対し、ai1s では、合法手 の着手を行う際に Marubatsu クラス の インスタンス の 深いコピー を作成するという、時間がかかる処理 を行っているからです。ルール 5、6、7 のように、着手を行う必要 がある処理の場合は、それほど 時間の差 は 生じない ので、一般的 には 評価値を利用 した アルゴリズム の 処理速度 が 大きく異なる ことは ありません。そのことは、次回の記事 で確認します。

評価値の設定の間違いに関する欠点

評価値を利用 する アルゴリズム では、確かに評価値を変えることで、条件の優先順位を柔軟に変えることができますが、評価値 の設定を 間違える と、先程 ai4s の四隅の評価値を変えた時にバグが発生したように、簡単に 間違った処理 が行われます。また、間違っていること に 気づきにくい、間違った場合 に 原因を発見しづらい という欠点があります。

今回の記事のまとめ

今回の記事では、評価値を利用 した アルゴリズム での、評価値 の 設定方法 と、計算方法 について説明し、ルール 1 と 4 の AI を 評価値を利用 した アルゴリズム で定義しました。

評価値を利用 した アルゴリズム では、「優先したいもの の 評価値 が、それより も 優先したくないもの の 評価値より も 大きくなる」という 条件を満たせば、評価値 に どのような値 を設定しても かまいません。

このように、評価値を利用 した アルゴリズム では、評価値 を 柔軟に設定 できますが、逆に言えば、間違った評価値 を 簡単に設定できてしまう ため、その点に 気をつけないと、簡単にバグが発生 してしまう点に注意する必要があります。

次回の記事では、評価値を利用 した アルゴリズム で、残りの ルール 5 ~ 7 を実装する方法について説明します。

本記事で入力したプログラム

以下のリンクから、本記事で入力して実行した JupyterLab のファイルを見ることができます。

今回の記事では、marubatsu.py は修正していないので、marubatsu_new.py はありません。

以下のリンクは、今回の記事で更新した ai.py です。

次回の記事

詳細は割愛しますが、インスタンスのハッシュ値を計算する処理をクラスの定義の中に、自分で記述することができます ↩ ↩²
fake は、偽物という意味の英語です ↩

You get articles that match your needs
You can efficiently read back useful information
You can use dark theme

What you can do with signing up

Pythonで〇×ゲームのAIを一から作成する その49 評価値の計算方法

目次と前回の記事

これまでに作成したモジュール

これまでに作成した AI

評価値を利用した ルール 1 で着手を行う AI の定義

ai1s の定義 その 1（if 文を使う方法）

動作の確認

ai1s の定義 その 2（list によるテーブルを使う方法）

ハッシュ可能なオブジェクトとハッシュ値

dict のキーにハッシュ可能なオブジェクトのみが利用できる理由

ハッシュ可能なオブジェクトの種類

ハッシュ値の取得方法

ハッシュ値の性質

テーブルを使った ai1s の定義

動作の確認

ai1s の定義 その 3（式で計算する方法）

デバッグ表示による動作の確認

対戦による動作の確認

ai1s の定義 その 4（最初の最善手を採用する）

ai_by_score の改良

ai1s の修正

動作の確認

仮引数 rand の処理の確認

評価値を利用した ルール 4 で着手を行う AI の定義

評価値の設定

ai4s の定義の方法

四隅のマスであることの判定方法

四隅を判定する式の記述方法

四隅を判定する式の別の記述方法

四隅のマスの評価値の計算

ai4s の定義と動作の確認

別の実装方法

ai4s の定義と動作の確認

バグの原因

ai4s の修正と動作の確認

評価値を利用したアルゴリズムの利点

評価値関数を記述するだけで、AI を定義できる

ランダムな選択を行うことができる

ルールの条件の優先順位を柔軟に変えることができる

評価値を利用したアルゴリズムの欠点

処理に時間がかかる場合がある

評価値の設定の間違いに関する欠点

今回の記事のまとめ

本記事で入力したプログラム

次回の記事

Pythonで〇×ゲームのAIを一から作成する　その49　評価値の計算方法

評価値を利用したルール 1 で着手を行う AI の定義

`ai1s` の定義その 1（if 文を使う方法）

`ai1s` の定義その 2（list によるテーブルを使う方法）

テーブルを使った `ai1s` の定義

`ai1s` の定義その 3（式で計算する方法）

`ai1s` の定義その 4（最初の最善手を採用する）

`ai_by_score` の改良

`ai1s` の修正

仮引数 `rand` の処理の確認

評価値を利用したルール 4 で着手を行う AI の定義

`ai4s` の定義の方法

`ai4s` の定義と動作の確認

`ai4s` の定義と動作の確認

`ai4s` の修正と動作の確認