Pythonで〇×ゲームのAIを一から作成する その44 ルールベースのAIとAIの検証

目次と前回の記事

これまでに作成したモジュール

以下のリンクから、これまでに作成したモジュールを見ることができます。

これまでに作成した AI

これまでに作成した AI の アルゴリズム は以下の通りです。

関数名	アルゴリズム
ai1	左上から順に空いているマスを探し、最初に見つかったマスに着手する
ai2	ランダムなマスに着手する

基準となる ai2 との 対戦結果（単位は %）は以下の通りです。太字は ai2 VS ai2 よりも成績が良い数値を表します。

関数名	o 勝	o 負	o 分	x 勝	x 負	x 分	勝	負	分
ai1	78.1	17.5	4.4	44.7	51.6	3.8	61.4	34.5	4.1
ai2	58.7	28.8	12.6	29.1	58.6	12.3	43.9	43.7	12.5

AI の種類

前回の記事で、AI の強さ を 評価 するための、AI どうしの対戦 を行う 環境 が整いましたので、今回の記事から、強い 〇× ゲームの AI の作成 を開始します。

〇× ゲームのような、ゲームの AI を作成する手法には、大きく分けて、ルールベース、探索型、機械学習型 の 3 種類があります¹。最初に、この中で、初期 の AI から よく使われてきた、ルールベースの AI について説明します。なお、この 3 種類の手法は、単独で利用される場合だけでなく、組み合わせて利用 される場合もあり、本記事でも紹介する予定です。

ルールベース の AI とは、解決すべき問題 に対する、人間の知識 を ルール化 し、その ルールに基づいて AI が 判断を行う という AI です。

ルールベースの AI には、主に以下のような 利点 と 欠点 があります。

• 利点
  • 問題 を 完全に解決 する 方法 を ルール化 できれば、ルールベース の AI を使って、100 % 正しい判断 を 行う ことが できる
  • ルール化 を 行う ことが できれば、ルール を if 文など の 条件分岐 を 組み合わせて記述 することが できる ので、プログラム を 記述しやすい
  • ルール を 順番 に 適用 することで 判断を行う ので、AI が行った 判断の理由 の 説明 がしやすい。また、その 結果を元 に、ルール の 評価 や 改良 を 行う ことが できる
• 欠点
  • 人間の知識をルール化するため、解決すべき問題 を、人間 が 熟知 している 必要 がある。例えば、将棋の AI を ルールベース で 作成 する場合は、将棋が強い 人 でなければ、強い AI を 作る ことは できない
  • ルール は、厳密 に 記述 する必要がある。そのため、理屈ではなく、感覚 で 行っている ようなことを ルール化 することは 困難 である。例えば、人間 が 歩く 際に、どのように 体を 動かしているか の ルール を、説明できる人 は ほとんどいない だろう
  • ルール をプログラムで 記述 するのが 困難 な 場合がある
  • 複雑な問題 の場合は、その 問題 を 完全に解決する方法 が 誰にもわからない 場合がある。そのような場合は、その問題に対する 不完全な知識 を ルール化 するしかないが、そのような AI が行う判断 も当然 不完全 なものになってしまう。例えば、勘違い などによって 間違ったルール化 を行ってしまうと、間違った判断 が行われてしまう
  • 問題解決のための ルール が 増えた 結果、収拾がつかなくなる 場合がある。例えば、ルールが 多くなりすぎ ると、AI が行った 判断 が、どのルール によって 行われた ものであるかの 判断がつけづらくなる。また、新しいルール を 作成 する際には、それまでのルール との 整合性 を気にしながら作成する必要があるため、ルールの数 が 多く なれば なるほど、新しいルール を 作成 するのが 困難 になる。

言葉の説明だけではよくわからないと思いますので、実際に 〇× ゲーム の AI を ルールベース で 作成 することで、上記の 利点 と 欠点 の一部について 説明 します。この先の説明を読む前に、〇× ゲームの強い AI を作るためのルールについて少し考えてみて下さい。

ai1 と ai2 の分類

実は、ai1 と ai2 は、ルールベース の AI に分類 されます。その理由は、ai1 の アルゴリズム である「左上から順に空いているマスを探し、最初に見つかったマスに着手する」と、ai2 の「ランダムなマスに着手する」は、いずれも 着手するマス を 決めるため の ルール だからです。ルールベース の AI の ルール は、AI の アルゴリズム であると 言い換えても良い でしょう。なお、ai1 と ai2 の ルール は、いずれも 強い AI を 作成する ための ルールではない 点が、これから作成する AI と異なります。

以後は、ai1 の「左上から順に空いているマスを探し、最初に見つかったマスに着手する」を ルール 1、ai2 の「ランダムなマスに着手する」を ルール 2 と 表記 し、わかりやすいように、今後作成する ルールの番号 と、AI の 関数の番号 を 合わせる ことにします。

ルール 3 （真ん中のマスに優先して着手する）

〇× ゲーム を ある程度遊んだ ことがある人は、真ん中 の (1, 1) のマスに 着手 すると 勝ちやすい ということが なんとなく理解 できるようになるのではないかと思います。そこで、そのこと と、ルール 2 を 組み合わせ た 下記のような ルール 3 が考えることにします。

1. 真ん中 の マス が 空いていれば、そこに着手 する
2. 真ん中 の マス が 空いていなければ、ランダム なマスに 着手 する

思いついたルール を 何も考えず に 実装 すると、見当違い な ルール であった場合に 時間の無駄 になるので、実装 を 行う前 に、その ルール が 有効であるか どうかについて、今回は簡単に 考察 することにします。当たり前だと思う人が多いかもしれませんが、真ん中 のマスに 着手 すると 勝ちやすい ことの 理由 について 論理的な説明 ができる人はどれくらいいるでしょうか？その理由について少し考えてみて下さい。

なお、ルール の 実装 が 簡単に行える 場合は、考察せず に AI を 実装 する場合もあります。

真ん中のマスへの着手が有利である理由の考察

真ん中のマス への 着手 が 有利である ことを 示す ためには、真ん中以外 のマスへの 着手 と 比較 する必要があります。その際に、他 の 8 マス すべてとの 比較 を行う 必要 は ありません。その 理由 は、〇× ゲーム の ゲーム盤 は 正方形 なので、ゲーム盤 を 90 度 ずつ、3 回 回転 した場合に、ゲーム盤 が ぴったり と 重なり、隅 の マス を、他の すべて の 隅のマス に 移動 することが できる からです。従って、4 つ の 隅のマス は 同じ性質を持つ と みなす ことができます。同様の理由 で、4 つ の 辺のマス も 同じ性質を持つ と みなす ことができるので、隅 と 辺 の 2 種類 のマスへの 着手 と 比較すればよい ことが分かります。

次に、有利である ことを 表す指標 を 決める 必要があります。わかりやすい指標 として、その マスに着手 することで、何種類 の 勝ち方が生じる かを 数える というものが 考えられます。具体的には、着手 した マスを含む、勝利の並び の 種類 を 数え ます。

下図は、真ん中 のマス、隅 のマス、辺 のマスの それぞれ に対して、その マスを含む、勝ち方 の 並び を 列挙 したものです。真ん中 のマスに 着手 することで、最も多い 4 種類の 勝ち方 があるので、この指標 では 真ん中の着手 が 最も有利 であることが分かります。

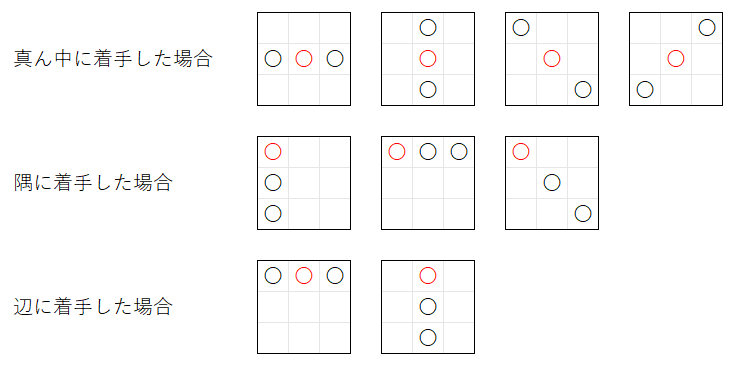
相手の立場 に立って 考える と、真ん中、隅、辺 に 着手 した場合は、それぞれ 上図の 勝ち方 を 相手から奪う ことになります。〇× ゲームの 勝ち方 は 横 3 通り、縦 3 通り、斜め 2 通り の 計 8 通り なので、真ん中に着手 することで、相手 の 勝ち方 を 最も少ない 8 - 4 = 4 通り に 限定 できます。その 4 通りは、下のような 図を書く ことで 確認 できます。

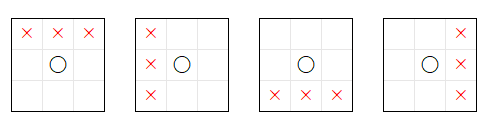
先程、ルールベース の AI には「人間の知識をルール化するため、解決すべき問題 を、人間 が 熟知 している 必要 がある」という 欠点 があると説明しましたが、〇×ゲーム の AI の ルール化 を行うためには、上記のような 〇×ゲームに関する知識 が必要になります。

ルールの作成時に厳密な証明が必要かどうか

上記の考察 では、「マスに着手 することで、何種類 の 勝ち方 が 生じる かを 数える」という、一見する と非常に もっともらしく見える 指標を使って、真ん中 のマスに 着手 をすることが 有利 であることを 示しました が、この指標 が 本当 に 有利 であることを 正確に示す 指標 であるか の 証明 は 行われていません。従って、上記の考察 から、真ん中 に 着手 することが 有利 である 可能性が高そう だということは 言えます が、絶対に有利 であるということが 証明 されたわけでは ありません。

理想的 には、ルール が 正しい ことを 厳密に証明したほうが良い ですが、実際 には 厳密な証明 が 困難 または 不可能 であることが良くあります。実際に、〇× ゲーム で、真ん中 のマスに 優先的に着手 する ルール が 正しい ことを 厳密に証明 することは かなり困難 です。どれだけ困難であるかは、今後の記事で実際に紹介する予定です。

従って、思いついたルール が 正しいか どうかの 厳密な証明 が 困難 な場合は、有利 である 可能性が高い ことが 分かった時点 で、とりあえず そのルールで AI を実装 し、他の AI と実際に 対戦 することで 強くなったかどうか を 検証する という方法を取るのが 一般的 です。検証 した 結果、その ルール で 強くなる ことが分かれば 採用 し、そうでなければ そのルールは 廃棄 します。また、その際に、その ルール で 強くなった（うまくいかなかった）理由 を 考察 することで、問題の性質 を 理解 し、既存のルール の 改良案 や、新しいルール の 作成 に つなげて いきます。これは、現実の世界 で、問題を解決する際 に、さまざまな方法 を 考案 し、実際 に 試した結果 で 判断する という、試行錯誤 を行う 手法と同じ です。

本記事でも、真ん中 のマスへの 着手 が 最も有利 であるという 厳密な証明 を 行わず に、とりあえず AI を作成 し、他の AI と 対戦 することで 検証を行う ことにします。

ai3 の実装

下記は、先程の ルール 3 を再掲したものです。このルール を元に ai3 を 実装 します。

1. 真ん中 の マス が 空いていれば、そこに着手 する
2. 真ん中 の マス が 空いていなければ、ランダム なマスに 着手 する

真ん中のマス が 空いていれば、そこに着手 するという処理は、ルールベースの利点 で説明したように if 文 による 条件分岐 を使って 簡単に記述 でき、ランダム なマスに 着手 する 処理 は、ai2 と 同じ処理 なので、ai3 は、下記のプログラムのように記述できます。

• 5、6 行目：真ん中 の マス である (1, 1) のマスが 空であるかどうか を if 文 で 判定 し、空の場会 は、着手 する マスの 座標 として、1, 1 を 返す
• 7、8 行目：真ん中 の マス が 空でない場合 は、ai2 と 同様の方法 で、合法手の中 から ランダム なマスを 選択 し、その 座標 を 返す

1  from marubatsu import Marubatsu
2  from random import choice
3
4  def ai3(mb):
5      if mb.board[1][1] == Marubatsu.EMPTY:
6          return 1, 1
7      legal_moves = mb.calc_legal_moves()
8      return choice(legal_moves)

行番号のないプログラム

from marubatsu import Marubatsu
from random import choice

def ai3(mb):
    if mb.board[1][1] == Marubatsu.EMPTY:
        return 1, 1
    legal_moves = mb.calc_legal_moves()
    return choice(legal_moves)

修正箇所（ai2 との比較です）

-def ai2(mb):
+def ai3(mb):
+   if mb.board[1][1] == Marubatsu.EMPTY:
+       return 1, 1
    legal_moves = mb.calc_legal_moves()
    return choice(legal_moves)

ai_match で 複数回の対戦 を 行う前 に、ai3 が 正しく実装されたか どうかを 確認 するために、play メソッドを使って、ai2 と 対戦 を行い、途中経過 を 表示 することにします。実行結果から、〇 を担当 する ai3 が、最初 に (1, 1) に 着手 することが 確認 できます。

本記事では ai3 が 〇 の担当 で 1 度 しか 確認 しませんが、心配な方 は ai3 が 〇 の担当 と、× の担当 で 何度か play メソッドを 実行 し、ai3 が、(1, 1) が 空いていれば そこに 必ず着手 することを 確認 して下さい。

本記事の 確認 では、対戦相手 を ランダムな着手 を行う ai2 としていますが、mb.play(ai=[ai3, None]) を 実行 して、人間相手で確認 することも できます。

from ai import ai1, ai2

mb = Marubatsu()
mb.play(ai=[ai3, ai2])

実行結果（実行結果はランダムなので下記とは異なる場合があります）

Turn o
...
...
...

Turn x
...
.O.
...

Turn o
.X.
.o.
...

Turn x
Ox.
.o.
...

Turn o
oxX
.o.
...

Turn x
oxx
.oO
...

Turn o
oxx
Xoo
...

winner o
oxx
xoo
..O

'o'

セルの最後の行の計算結果の表示

以前の記事のノートで簡単に説明しましたが、JupyterLab では、セル の 最後の行 の 式の計算結果 が、print を 記述しなくても表示 されます。上記の実行結果の 最後 に表示される o は、mb.play(ai=[ai3, ai2]) の 返り値 です。

セル の 最後の行 の 計算結果 が 表示されない ようにする 方法 として、下記のプログラムのように、行の最後 に 半角の ;（セミコロン） を 記述 するという 方法 があります。なお、実行結果は、最後に o などが表示されなくなるだけなので省略します。

mb.play(ai=[ai3, ai2]);

; は、文 を 区切る記号 で、例えば、a = 1; b = 2 のように 文 を ; で区切る ことで、1 行 に 2 つ以上 の 文 を 記述 することが できます。上記のように 行の最後 に ; を 記述 することで、mb.play(ai=[ai3, ai2]) が、その 行 で 最後に計算された式 とは みなされなくなる ので、mb.play(ai=[ai3, ai2]) の 計算結果 が、表示されなく なります。以後は、セルの 最後の行 の 計算結果 を 表示したくない場合 に、行の最後 に ; を記述 することにします。

print の表示との違い

以前の記事のノートでも簡単に説明しましたが、セル の 最後の行 の 式の計算結果 の 表示 と、print による 式の計算結果 の 表示 が 異なる場合 があります。

例えば、None は、下記のプログラムのように、セル の 最後の行 に 記述 した場合と、print で 表示 した場合は、表示の結果 が 異なります。

最後の行 の 式 の 計算結果 が None の 場合 は 何も表示されません。

None

実行結果

print で None を 表示 した 場合 は、None が 表示 されます。

print(None)

実行結果

None

下記のプログラムのように、セル の 最後の行 で ai_match を 実行 した場合に、余計な表示 が 行われない のは、ai_match が return 文 によって 値を返さない関数 だからです。以前の記事で説明したように、return 文 で 終了しない 関数は、関数の 返り値 として None が返り、その None は 画面に表示されない ので、余計な表示 は 行われません。

ai_match(ai=[ai3, ai1])

下記のような、セル の 最後の行 で print で 表示を行う プログラムで、余計な表示 が 行われない理由 も、print が None を 返り値 として 返すから です。

print(1)

実行結果

1

セル の 最後の行 の 計算結果 の 表示 と、print による 表示 が 異なる場合がある理由 は、セル の 最後の行 の 計算結果 が、オブジェクト の __repr__ メソッドを使って 文字列に変換 したものを 表示 するのに対し、print が オブジェクト の __str__ メソッドを使って 文字列に変換 したものを 表示 するからです。

__repr__ メソッドと、__str__ メソッドの 違い については、以前の記事 のリンク先をスクロールした所にある ノートを参照 して下さい。

ai2 との対戦

ai3 が実装できたので、下記のプログラムで、基準 となる ai2 と 対戦 します。

from ai import ai_match

ai_match(ai=[ai3, ai2])

実行結果（実行結果はランダムなので下記とは異なる場合があります）

ai3 VS ai2
count     win    lose    draw
o        6932    1922    1146
x        3885    4765    1350
total   10817    6687    2496

ratio     win    lose    draw
o       69.3%   19.2%   11.5%
x       38.9%   47.6%   13.5%
total   54.1%   33.4%   12.5%

下記は、上記の結果を表に加えたものです。

関数名	o 勝	o 負	o 分	x 勝	x 負	x 分	勝	負	分
ai1	78.1	17.5	4.4	44.7	51.6	3.8	61.4	34.5	4.1
ai2	58.7	28.8	12.6	29.1	58.6	12.3	43.9	43.7	12.5
ai3	69.3	19.2	11.5	38.9	47.6	13.5	54.1	33.4	12.5

表から、ai1 程ではありませんが、ai3 は、ai2 に 対して強い AI であることがわかります。このように、適切なルール であれば、ルール 3 のような 非常に単純なルール であっても、AI の強さ を 向上 させることが 可能 です。

ai1 との対戦

次に、下記のプログラムで、ai3 と ai1 の 対戦 を行います。

ai_match(ai=[ai3, ai1])

実行結果（実行結果はランダムなので下記とは異なる場合があります）

ai3 VS ai1
count     win    lose    draw
o        3666    5663     671
x         838    9162       0
total    4504   14825     671

ratio     win    lose    draw
o       36.7%   56.6%    6.7%
x        8.4%   91.6%    0.0%
total   22.5%   74.1%    3.4%

また、比較 を行うために、ai2 から見た ai1 との 対戦 を行います。

ai_match(ai=[ai2, ai1])

実行結果（実行結果はランダムなので下記とは異なる場合があります）

ai2 VS ai1
count     win    lose    draw
o        5138    4459     403
x        1740    7844     416
total    6878   12303     819

ratio     win    lose    draw
o       51.4%   44.6%    4.0%
x       17.4%   78.4%    4.2%
total   34.4%   61.5%    4.1%

下記は、上記の結果を表にまとめたものです。

関数名	o 勝	o 負	o 分	x 勝	x 負	x 分	勝	負	分
ai3 VS ai1	36.7	56.6	6.7	8.4	91.6	0.0	22.5	74.1	3.4
ai2 VS ai1	51.4	44.6	4.0	17.4	78.4	4.2	34.4	61.5	4.1

表から、ai3 は ai1 に 対して 全体 で 勝率 が 22.5% と 大きく負け越している ことが分かります。また、x の手番 の場合は、勝率 が 8.4% と とんでもなく低い ことが分かります。

さらに、ai2 VS ai1 の 結果 と 比較 すると、ai2 より も、ai3 のほうが ai1 に対して さらに 成績が悪い ことが分かります。先ほどの、ai3 VS ai2 の結果では、ai3 が ai2 に 対して 強い ことがわかりましたが、ai1 と対戦 した場合は、ai2 のほう が、ai3 より も ai1 に 対して 強い という 逆の結果 になることがわかります。

強さ を 不等号 の 記号 で表す（大きいほう が 強い）と、下記のようになります。

• ai3 VS ai2 では、ai3 > ai2 である
• ai1 に 対する戦績 では、ai2 > ai3 である

以前に説明したことの繰り返しになりますが、上記のように、特定の AI との 対戦結果 は、対戦 した AI の間 の 相対的 な 強さ のみ 測ります。全体的 な 強さ を 測る ためには、さまざま な AI と 対戦 した 結果 を 検証 する 必要 があります。

本記事の最初で述べたように、ルールベース の AI の 利点 の一つに、「AI が行った 判断の理由 の 説明 がしやすい」というものがあります。実際に、上記のような 逆の結果 になる 理由 を 考察 することが できる ので、その理由について少し考えてみて下さい。

対戦結果の考察

このような結果になった 理由 を調べるためには、それぞれ の 組み合わせ で どのような対戦 が　行われる かを 考察 する必要があります。そのような考察は、以前の記事で説明した、「ai1 が ai2 に勝ち越す理由」で既に行っており、今回も 同様の考察 を行います。

今回は、ai3 が 〇 を担当 する場合と、× を担当 する場合に 分けて考察 します。

用語の説明

〇 や × を 担当する AI が、何手目 の 着手 を 行ったか を「〇 の 1 手目の着手」、全体 で 何手目 の 着手 を 行ったか を「1 手目の着手」のように 表記 すると、「手目」という 表記 の 意味 が まぎらわしくなる ので、本記事では以降は、〇 や × の 手数 は「〇 の 1 回目 の着手」、全体の手数は「1 手目 の着手」のように、区別 して 表記 することにします。

ai3 が 〇 を担当する場合

ai1 は、左上のマス から 順番 に 空いているマス に 着手 を行うので、ai3 が 〇 を担当する場合 には、3 回目まで に、上の行 の いずれか の マスに着手 を行わなければ 敗北 してしまいます。しかし、ai3 は 1 回目 で 必ず 真ん中の (1, 1) に 着手を行う ので、残りの 2 回 で、上の行 の いずれかのマス に 着手 を行わなければなりません。従って、ai2 よりも、不利な状況 で ai1 と 対戦 することになり、ai2 VS ai1 よりも 対戦成績 が 悪く なります。

以前の記事では失念していましたが、ai3 が 〇 を担当 する場合は、3 回目まで に、2 行目 の (0, 1)、(1, 1)、(2, 1) の 3 マスに 着手 を行うことで、ai1 より先 に 勝利 する 場合 が あります。ただし、詳しい計算方法は省略しましすが、ai3 VS ai1 で、ai3 が 3 回目まで に 2 行目 の 3 マスに 着手 して 勝利 する 確率 は 約 5% 程度 しかない ので、上記の考察 に 大きな影響 は 与えません。

ai2 VS ai1 で ai2 が 3 回目まで に 2 行目 または 3 行目 の 3 マスに 着手 して 勝利 する 確率 は 約 4% なので、前回の記事 の 考察 にも 大きな影響 は 与えません。

ai3 が × を担当する場合

この場合は、ai3 は 2 回目まで に、上の行 の いずれかのマス に 着手 を 行う必要 がありますが、ai1 は 1 回目 で 必ず (0, 0) に 着手を行う ため、ai3 の 1 回目 では 真ん中 の マス が 空いている ので、必ず (1, 1) に 着手 を行います。さらに、ai1 は 2 回目 で 必ず (1, 0) に 着手 を行うので、ai3 は 2 回目 で残った 6 マスの中 から (2, 0) に 着手 を行わなければ 負けてしまいます します。従って、この場合も ai3 は、ai2 よりも、不利な状況 で ai1 と 対戦 することになり、ai2 VS ai1 よりも 対戦成績 が 悪く なります。

図で書くと、ai3 が × を担当 する場合は、3 手目まで は、必ず下図 の 着手 が 行われます。× の 2 回目 の 着手 で、黄色いマス に 着手 を 行わなければ、その次 に 〇 が 黄色のマス に 着手 して × は敗北 しますが、阻止 する 確率 は 1/6 = 約 16.7 % しかありません。

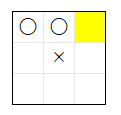
考察のまとめ

上記のことから、ai3 は、どちらの手番 でも 1 回目 で 必ず (1, 1) に 着手 を行うため、ai2 が 一番上の行 で 3 回の着手 で 勝利 しようとする 場合 に対して、ランダムな着手 で 邪魔をする機会 が ai2 より も 1 回分減ってしまう ことになります。そのため、ai3 VS ai1 の 対戦成績 は、ai2 VS ai1 よりも 下がって しまいます。

ただし、この結果は、ai3 の アルゴリズム が ai1 の アルゴリズムに 対して 極端に相性が悪い せいです。ai3 VS ai1 と ai2 VS ai1 の 結果だけ から、一般的 に見て ai2 と ai3 の どちらが強いか を 判断 することは できない 点に 注意 して下さい。一般的な強さ については、他のさまざまな AI と 対戦 し、総合的 に 判断 する 必要 があります。

ai3 との対戦

せっかくなので、さらに ai3 どうし で 対戦 させてみることにします。

ai_match(ai=[ai3, ai3])

実行結果（実行結果はランダムなので下記とは異なる場合があります）

ai3 VS ai3
count     win    lose    draw
o        6801    2000    1199
x        1919    6939    1142
total    8720    8939    2341

ratio     win    lose    draw
o       68.0%   20.0%   12.0%
x       19.2%   69.4%   11.4%
total   43.6%   44.7%   11.7%

下記は、上記の結果と ai3 VS ai2 の対戦結果を表にまとめたものです。

関数名	o 勝	o 負	o 分	x 勝	x 負	x 分	勝	負	分
ai3 VS ai3	68.0	20.0	12.0	19.2	69.4	11.4	43.6	44.7	11.7
ai3 VS ai2	69.2	18.9	11.8	39.1	47.0	13.9	54.1	33.0	12.9

表から、ai3 が 〇 を担当 した場合は、相手 が ai2 と ai3 の場合で、対戦成績 が ほとんど変わらない が、× を担当 した場合は、相手 が ai2 のほう が 対戦成績が良くなる ことが分かります。このような結果になる理由について少し考えてみて下さい。

先程と同様に、ai3 が 〇 を担当 する場合と、× を担当 する場合に 分けて考察 します。

ai3 が 〇 を担当する場合

ai3 VS ai3 の場合は、必ず最初 に (1, 1) に 着手が行われる ので、× を担当 する ai3 は、1 回目 で (1, 1) が 空ではありません。従って、× を担当 する ai3 の すべての手番 で ランダムなマス に 着手 を行うことになるので、ai3 VS ai2 で ai2 が × を担当する場合と 全く同じ処理 が行われることになります。そのため、ai3 が 〇 を担当 する場合は、相手が ai2 と ai3 の場合で、対戦成績 が ほぼ同じ になります。

ai3 が × を担当する場合

ai3 VS ai3 の場合は、× を担当 する ai3 は、1 回目 で (1, 1) が 空ではない ので、真ん中 に 着手 することは できません が、ai2 VS ai3 の場合は 1 回目で ai2 が (1, 1) に 着手 を行うとは 限らない ので、有利 になる (1, 1) に 着手できる可能性 があります。そのため、ai2 と対戦する方が、ai3 と対戦するよりも 対戦成績 が 良く なります。

このように、作成した AI の間で、さまざまな組み合わせ で 対戦 を行い、その 結果 を 考察 することで、さまざまな ことが わかる ようになります。また、わかったこと を 利用 して、ルール の 欠点 や、改良点 を 見つける ことが できる場合 があるので、考察 は 重要 です。

ただし、作成 した AI の数 が 多くなる と、組み合わせ の 数 が 多くなりすぎる ので、今後 は今回のように、すべて の 組み合わせ で 対戦 を行うことは しません。

ルール 4（四隅のマスに優先して着手する）

ルール 3 では、真ん中 の マス に 優先して着手 を行いますが、真ん中 の マス が 埋まっている 場合に、次に有利 だと考えられる 四隅 の いずれか の マス に 着手 するという ルール 4 が考えられます。ただし、四隅 の いずれか のマスに 着手 する 処理 は、プログラムの 記述 が 複雑 になるので、ai1 の アルゴリズム と 同様 に、下記のような、左上のマス から 順に、四隅のマス を 調べ、最初 に 見つかった、空いているマス に 着手 することにします。

1. 真ん中 の マス が 空いていれば 、そこに着手 する
2. 真ん中 の マス が 空いていなければ、次に 四隅のマス を 左上 から 順に調べ、最初 に 見つかった、空いているマス に 着手 する
3. 四隅 も 空いていなければ、ランダムなマス に 着手 する

この ルール 4 で 本当 に AI が 強くなるか どうかを 考察 することは 可能 ですが、思いついたルール で AI を作成 し、他の AI と 対戦 を行った 結果 から 考察 したほうが 分かりやすい 場合があるので、AI を 簡単に実装できる場合 などでは、思いついたルール を 考察せず に 実装 することも 良くあります。そこで、今回は 先に この ルール 4 が 良いか どうかの 考察 を 行わず に、ai4 を 作成 して他の AI と 対戦 した 結果 をから 考察 することにします。

下記は、上記の ルール 4 で着手を行う、ai4 を定義するプログラムです。

• 4 ~ 7 行目：四隅のマス の 座標 は、(0, 0)、(0, 2)、(2, 0)、(2, 2) なので、x 座標 と y 座標 を 0 から 3 未満 まで 2 ずつ増やし ながら 繰り返し処理 を行うことで、左上 の マス から 順番 に、四隅 の マスの座標 を 調べる ことができる。2 ずつ増やし ながら行う 繰り返し処理 は、以前の記事で説明した、range の step を使って range(0, 3, 2) のように 記述 できる。それ以外 の部分は、ai1 の 処理と同様 の 方法 で 記述 できる

1  def ai4(mb):
2      if mb.board[1][1] == Marubatsu.EMPTY:
3          return 1, 1
4      for y in range(0, 3, 2):
5          for x in range(0, 3, 2):
6              if mb.board[x][y] == Marubatsu.EMPTY:
7                  return x, y
8      legal_moves = mb.calc_legal_moves()
9      return choice(legal_moves)

行番号のないプログラム

def ai4(mb):
    if mb.board[1][1] == Marubatsu.EMPTY:
        return 1, 1
    for y in range(0, 3, 2):
        for x in range(0, 3, 2):
            if mb.board[x][y] == Marubatsu.EMPTY:
                return x, y
    legal_moves = mb.calc_legal_moves()
    return choice(legal_moves)

修正箇所（ai3 との比較です）

-def ai3(mb):
+def ai4(mb):
    if mb.board[1][1] == Marubatsu.EMPTY:
        return 1, 1
+   for y in range(0, 3, 2):
+       for x in range(0, 3, 2):
+           if mb.board[x][y] == Marubatsu.EMPTY:
+               return x, y
    legal_moves = mb.calc_legal_moves()
    return choice(legal_moves)

次に、ai4 が 正しく実装されたか どうかを 確認 します。実行結果から、〇 を担当 する ai4 が、1 回目 で (1, 1) に 着手した後 で、空いている四隅 の マス に、左上 から 順番 に 着手 を 行い、四隅 が 埋まった後 は ランダム な 着手 を行うことが 確認 できます。

mb.play(ai=[ai4, ai2]);

実行結果（実行結果はランダムなので下記とは異なる場合があります）

Turn o
...
...
...

Turn x
...
.O.
...

Turn o
.X.
.o.
...

Turn x
Ox.
.o.
...

Turn o
ox.
.o.
..X

Turn x
oxO
.o.
..x

Turn o
oxo
.o.
X.x

Turn x
oxo
.oO
x.x

Turn o
oxo
Xoo
x.x

winner draw
oxo
xoo
xOx

ai2 との対戦

ai4 が実装できたので、下記のプログラムで、基準 となる ai2 と対戦 します。

ai_match(ai=[ai4, ai2])

実行結果（実行結果はランダムなので下記とは異なる場合があります）

ai4 VS ai2
count     win    lose    draw
o        8303     952     745
x        5723    3304     973
total   14026    4256    1718

ratio     win    lose    draw
o       83.0%    9.5%    7.4%
x       57.2%   33.0%    9.7%
total   70.1%   21.3%    8.6%

下記は、上記の結果を表に加えたものです。

関数名	o 勝	o 負	o 分	x 勝	x 負	x 分	勝	負	分
ai1	78.1	17.5	4.4	44.7	51.6	3.8	61.4	34.5	4.1
ai2	58.7	28.8	12.6	29.1	58.6	12.3	43.9	43.7	12.5
ai3	69.3	19.2	11.5	38.9	47.6	13.5	54.1	33.4	12.5
ai4	83.0	9.5	7.4	57.2	33.0	9.7	70.1	21.3	8.6

表から、ai4 は、ai2 に 対して、ai1 より も 強い AI であることがわかります。なお、ai4 VS ai2 の 対戦結果 の 考察 については、この後 の ai3 との対戦 の所で 行います。

ai1 との対戦

次に、ai1 との 強さを比較 するために、下記のプログラムで ai1 と対戦 します。

ai_match(ai=[ai4, ai1])

実行結果

ai4 VS ai1
count     win    lose    draw
o       10000       0       0
x       10000       0       0
total   20000       0       0

ratio     win    lose    draw
o      100.0%    0.0%    0.0%
x      100.0%    0.0%    0.0%
total  100.0%    0.0%    0.0%

実行結果から、ai4 は ai1 に 100% 勝利 することが分かりました。その 理由 は、実際に、下記のプログラムのように、play メソッドで 1 回 ずつ 手番を入れ替えて対戦 して 表示 される 途中経過 を 見て考察 するのが わかりやすい でしょう。

ai4 が 〇 を担当する場合

ai4 と ai1 の アルゴリズム から、必ず 下記のように、〇 (1, 1)、× (0, 0)、〇 (2, 0)、× (1, 0)、〇 (0, 2) の 順 で 着手 が行われ、ai4 が 担当する 〇 が 勝利 します。

mb.play(ai=[ai4, ai1]);

実行結果

Turn o
...
...
...

Turn x
...
.O.
...

Turn o
X..
.o.
...

Turn x
x.O
.o.
...

Turn o
xXo
.o.
...

winner o
xxo
.o.
O..

ai4 が 〇 を担当する場合

ai4 と ai1 の アルゴリズム から、必ず 下記のように、〇 (0, 0)、× (1, 1)、〇 (1, 0)、× (2, 0)、〇 (0, 1)、× (0, 2) の 順 で 着手 が行われ、ai4 が 担当する × が 勝利 します。

mb.play(ai=[ai1, ai4]);

実行結果

Turn o
...
...
...

Turn x
O..
...
...

Turn o
o..
.X.
...

Turn x
oO.
.x.
...

Turn o
ooX
.x.
...

Turn x
oox
Ox.
...

winner x
oox
ox.
X..

この 結果 から、やはり ai1 は 強い AI であるとは 言えなさそう であることが分かりました。従って、以後は 新しい AI を作成 した際に、ai1 との対戦 は 省略 することにします。

ai3 との対戦

次に、下記のプログラムで ai3 と対戦することにします。

ai_match(ai=[ai4, ai3])

実行結果

ai4 VS ai3
count     win    lose    draw
o        8313     945     742
x        2735    7014     251
total   11048    7959     993

ratio     win    lose    draw
o       83.1%    9.4%    7.4%
x       27.4%   70.1%    2.5%
total   55.2%   39.8%    5.0%

下記は、上記の結果を表に加えたものです。なお、上 の 4 つ は ai2 と対戦 した結果です。

関数名	o 勝	o 負	o 分	x 勝	x 負	x 分	勝	負	分
ai1	78.1	17.5	4.4	44.7	51.6	3.8	61.4	34.5	4.1
ai2	58.7	28.8	12.6	29.1	58.6	12.3	43.9	43.7	12.5
ai3	69.3	19.2	11.5	38.9	47.6	13.5	54.1	33.4	12.5
ai4	83.0	9.5	7.4	57.2	33.0	9.7	70.1	21.3	8.6
ai4 VS ai3	83.1	9.4	7.4	27.4	70.1	2.5	55.2	39.8	5.0

実行結果から、ai4 は、〇 を担当 する場合は、ai3 に 対して 83.1% の 勝率 で 大きく勝ち越し ます。その理由について少し考えてみて下さい。

一方、× を担当 する場合は、勝率 が 27.4% しか なく、敗率 は 70.1% も あります。特に、この 70.1% という 敗率 は、他の AI が × を担当 して ai2 と対戦 したどの 結果 よりも、かなり大きい ので、この ルール 4 には何か 大きな欠陥 が 潜んでいそう です。その欠陥が何かについて少し考えてみて下さい。

ai4 が 〇 を担当する場合

ai4 は、〇 を担当 した場合、必ず 1 回目 で (1, 1) に 着手 を行うので、× を担当 する ai2 または ai3 は、すべて の 着手 で ランダム な 着手 を行います。そのため、ai4 VS ai3 と、ai4 VS ai2 では、× を ai2 が担当 しても、ai3 が担当 しても 全く同じ処理 が行われます。従って、ai4 VS ai2 と ai4 VS ai3 の 対戦成績 は ほぼ同じ になります。

「ai2 または ai3」 のような 記述 は 冗長 なので、以後 の 「ai4 が 〇を担当する場合」の 説明 では ai3 に ついてのみ言及 することにします。

ai4 は、2 回目以降 は、(0, 0)、(2, 0)、(0, 2)、(2, 2) の 順 で 空いているマス に 着手 を行いますが、1 回目で (1, 1) に 〇 が配置済 なので、(0, 0)、(2, 2) または、(2, 0)、(0, 2) の 2 つのマス に 着手 できれば ai4 の 勝利 になります。ai3 は、ランダム なマスに 着手を行う ため、それを阻止 するような 着手 を偶然行う 確率 は、直観的 に 低そう で、実際に、先程の表の ai4 VS ai3 の 対戦成績 は ai4 が 80% 以上 で 大きく勝ち越し ます。このことから、ai3 は、〇 を担当 する ai4 にとって かなり相性が良い と 考察 できます。

現実の世界 では、結果 に対する 原因 を 説明できない 場合もあり、そのような場合は、例えば ai4 が ai3 に 大きく勝ち越す という 結果 だけを 重要視 します。なお、そのような場合は、原因 が わからない ので、結果の改善 は 困難 です。

おおまかな確率の計算

上記の 考察 は、直観的 なものなので、仮説 にすぎません。本当に正しいか どうかを 確認 するためには、〇 が勝利 する 場合 の 確率 を 計算 する 必要 があります。

〇 が 勝利 する 正確な確率 を 計算 するのは かなり面倒 ですが、多くの場合では、AI どうし の 強さの考察 を行う際に、確率 を 厳密に計算 する 必要 は ありません。以前の記事でも、おおまかな確率 を 計算 する 例を紹介 しましたが、今回の記事でも 大まかな確率 を 計算 することで、上記の考察 が 正しいそう であるかどうかを 確認 することにします。

多くの方には関係のない話になると思いますが、論文で発表 する 場合など では、厳密な確率 を 計算 する 必要 があります。

ai4 VS ai3 の着手の、おおまかな組み合わせの数の計算

〇 が勝利 する 確率 を 計算 するためには、ai4 VS ai3 で行われる 着手 の大まかな 組み合わせの数 を 計算 する 必要 があります。

ai4 は、5 箇所 の マス に 優先的 に 着手 を行うので、〇 の 3 回目 の 着手 を行う 5 手目まで で、その すべて のマスが 埋まる ことは ありません。そのため、〇 の 3 回目 の 着手 が ランダム に 行われる ことは ありません。従って、6 手目まで の 着手 の組み合わせは、ランダム に行われる × の 3 回 の 着手 の 組み合わせだけ を 考慮 することで、おおまかに、8 * 6 * 4 = 約 192 通り と 計算 することができます。

× の 1 回目 の 着手 は 2 手目 なので 残り の マスの数 は 8、2 回目 の 着手 は 4 手目 なので 残り の マスの数 は 6、3 回目 の 着手 は 残り の マスの数 は 4 となります。

もちろん、5 手目 に ゲームが決着する場合 や、7 手以上 の ゲームが存在 するので、この組み合わせの数 は ai4 VS ai2 がとりうる 着手の組み合わせ の数と 一致しません が、近い数字 である 可能性が高い ので、この 数値 をおおまかな 全体の組み合わせの数 とします。

〇 が勝利する場合のおおまかな確率の計算

厳密ではありません が、〇 が勝利 するのは、主に以下の図ような場合です。例外 として、先に × が勝利 する場合や、斜め以外 の 方向 で 〇 が勝利 する場合がありますが、それほど 確率は高くなさそう なので、とりあえず 無視 することにします。

下図は、〇 を担当 する ai4 が (0, 0)、(2, 0)、(0, 2)、(2, 2) の いずれか の マスに着手 することで 勝利 する 5 つのケース を表しています。図の 赤色のマス は、〇 が マスの中 に記述された 回数 の 手番で そのマスに 着手を行う ことを表しています。青色のマス は、× が、マスの中 に記述された 回数以下 の 手番 でそのマスに 着手を行う ことを表します。

この 5 通り が ピンとこない 方は、ai4 と ai3 の アルゴリズム通り に、実際 に 何度か 〇×ゲームの 着手 を 紙に書いて 確認してみると良いでしょう。

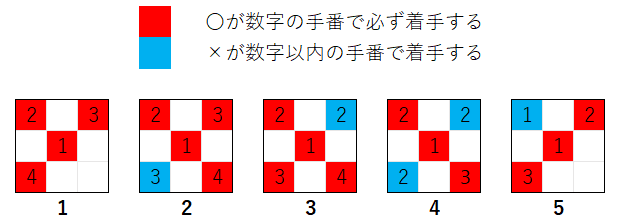
分かりづらいと思いますので、図の 1 と 2 と 4 について説明します。

図の 1 は、〇 が (1, 1)、(0, 0)、(2, 0)、(0, 2) の 順 で 着手 を行って 勝利 する 場合 を表しています。× は、3 回 の 手番 で、白色 の 5 つのマス の いずれか に 着手 を行います。

図の 2 は、〇 が (1, 1)、(0, 0)、(2, 0)、(2, 2) の 順 で 着手 を行って 勝利 する 場合 を表しています。× は、3 回目 までの いずれか の 手番 で、(0, 2) のマスに 着手 し、それ以外 の 2 回 の手番で、白色 の 4 つのマス の いずれか に 着手 を行います。その 理由 は、3 回目まで に × が (0, 2) に 着手 を 行わない と、先に 〇 が (0, 2) に 着手してしまう からです。

図の 4 は、〇 が (1, 1)、(0, 0)、(2, 2) の 順 で 着手 を行って 勝利 する 場合 を表しています。図の 2 と 同様の理由 で × は、1 回目 と 2 回目 の手番で、(2, 0) 、(0, 2) または (0, 2)、(2, 0) の 順番 で 着手 を行います。

下記の表は、それぞれの図の 番号 の 着手 が行われる 手順 の 組み合わせ を表します。

番号	x の 1 手目	x の 2 手目	x の 3 手目	組み合わせ	合計
1	5 通り	4 通り	3 通り	5 * 4 * 3 = 60	60
2	(0, 2) 4 通り 4 通り	4 通り (0, 2) 4 通り	3 通り 3 通り (0, 2)	4 * 3 = 12 4 * 3 = 12 4 * 3 = 12	36
3	(2, 0) 4 通り	4 通り (2, 0)	3 通り 3 通り	4 * 3 = 12 4 * 3 = 12	24
4	(2, 0) (0, 2)	(0, 2) (2, 0)	4 通り 4 通り	4 4	8
5	(0, 0)	5 通り		5	5

表から、すべての組み合わせ は 60 + 36 + 24 + 8 + 5 = 133 通り であることがわかります。

先ほど計算した、全体 の 組み合わせの数 である 192 通り を 利用 することで、おおまかな 〇 の勝率 を 133 / 192 = 約 69.3% と 計算 することができます。この 計算結果 は、先程の 考察 の、〇 が勝利しやすい ことを 裏付け ています。また、上記以外 の 手順 で 〇 が勝利 する 場合もある ことを 考慮 すると、先ほどの表の ai4 VS ai3 の 〇 の勝率 の 83.1% と 近い数字 と言えるので、おおまかな計算結果 の 精度 が 妥当 であることが 確認 できます。

× が勝利する場合のおおまかな確率の計算

せっかくなので、× が 勝利 する場合の 大まかな確率 も 計算 してみることにします。

下図は、× を担当 する ai3 が 先に勝利する場合 を 列挙 したものです。図から、× が先に勝利 する 着手 の 組み合わせ が 16 通り であることがわかります。

図の 数字 は、全体 の 着手の順番 を表し、赤 が 〇 が 100% その 手番で マスに 着手を行う ことを、オレンジ が 〇 がランダム にその 手番で マスに 着手を行う ことを、青 が × がランダム にその 手番で マスに 着手を行う ことを表します。

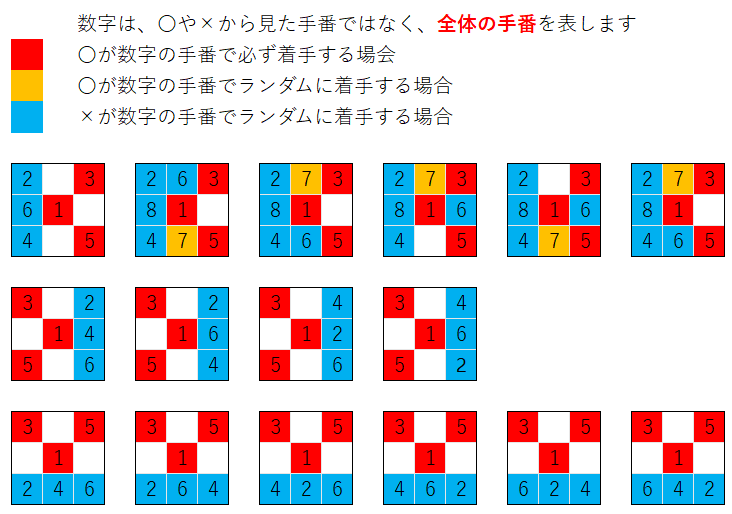
従って、× の勝率 は おおまか に 16 / 192 = 約 8.3% と 計算 することができ、先程の ai4 VS ai3 の 表 の 〇 の 敗率 の 9.4% と ほぼ一致する ことが分かります。

上記の、大まかな確率 の 計算結果 により、先程行った 考察 が 100% ではありませんが、おおむね正しそう であることが 確認 できました。

ai4 が × を担当する場合

ai4 が × を担当 する場合は、ai3 は、1 回目 で 必ず (1, 1) に 着手 を行います。その後、ai4 は (0, 0)、(2, 0)、(0, 2)、(2, 2) の 順 で マス が 空いていれば着手 を行おうとしますが、〇× ゲームでは、× の手番 は 最大 で 4 回 しか回ってこないので、4 回 の 着手 で そのすべてのマス が 空いていた場合 は、下図の ような 着手を行う ことになるため、× が勝利 することは ありません。つまり、〇 が 1 回目 で (1, 1) に 着手 を 行った場合 は、ai4 は、勝利を目指す着手 を 行わない ということです。これが、ai3 に 大きく負け越す原因 です。

一方、ai2 は 1 回目 で (1, 1) に 着手 を行う 確率 は 1/9 = 約 11% なので、上記 のような 非常に不利な状況 になる 確率 は約 11 % しかありません。また、ai2 が 1 回目 で (1, 1) に 着手 を 行わない 場合は、ai4 が (1, 1) に 着手を行います。もちろん、先に ai2 が どこかのマス に 着手 を行っているので、ai4 が 〇 を担当 する 場合 よりは 勝率は下がり ますが、先程の考察から 高い勝率 が 期待 できます。実際 に先程の ai4 VS ai2 の 表 の × の 勝率 の 57.2% が示すように、高い勝率 が得られています。

ルール 4 の評価

上記のことから、ai4 の ルール 4 は、ai1 や ai2 に対しては 強い AI であるかもしれませんが、実際 には 大きな欠陥 のある ルール であることがわかりました。

従って、本記事では ai4 を 欠陥のある AI と 判断する ことにします。

ルール 4 は、本記事の最初で説明した ルールベース の AI の 欠点 の「勘違い などによって 間違ったルール化 を行ってしまうと、間違った判断 が行われてしまう」の実例です。一見 すると 有効そう に 見える ルールが、必ずしも強い AI に 結びつかないことがある ことが、ルールベース の AI の作成 の 難しい所 です。従って、思いついたルール が 本当に有効か どうかについては、必ず検証する必要 があることを 忘れないように して下さい。

なお、思い付き の アイディア が 常に悪い というわけではありません。見込みのなさそう な アイディア を ダメ元 で 実装 したら うまくいった ということもあるからです。

今回の記事のまとめ

今回は、以下の表のようなアルゴリズムの ai3 と ai4 を実装し、他の AI と 対戦 することで、それぞれの アルゴリズム を 検証 しました。

関数名	アルゴリズム	欠陥
ai3	真ん中 のマスに 優先的 に 着手 する 既に 埋まっていた場合 は ランダム なマスに 着手 する
ai4	真ん中、隅 のマスの 順 で 優先的 に 着手 する 既に 埋まっていた場合 は ランダム なマスに 着手 する	あり

ai3、ai4 は、どちらも、基準 となる ai2 より 強くなる ことを 確認 できましたが、ai4 の アルゴリズム には 欠陥 があることが 判明 しました。

本記事で入力したプログラム

以下のリンクから、本記事で入力して実行した JupyterLab のファイルを見ることができます。

今回の記事では、marubatsu.py は修正していないので、marubatsu_new.py はありません。

以下のリンクは、今回の記事で更新した ai.py です。

次回の記事

1. 実際には、他にも分類の方法がありますが、本記事ではこの 3 つで分類することにします ↩