Pythonで〇×ゲームのAIを一から作成する その46 相手の勝利を阻止するAI

目次と前回の記事

これまでに作成したモジュール

以下のリンクから、これまでに作成したモジュールを見ることができます。

これまでに作成した AI

これまでに作成した AI の アルゴリズム は以下の通りです。

関数名	アルゴリズム
ai1	左上から順 に 空いているマス を探し、最初に見つかったマス に 着手 する
ai2	ランダム なマスに 着手 する
ai3	真ん中 のマスに 優先的 に 着手 する 既に 埋まっていた場合 は ランダム なマスに 着手 する
ai4	真ん中、隅 のマスの 順 で 優先的 に 着手 する 既に 埋まっていた場合 は ランダム なマスに 着手 する
ai5	勝てる場合 に 勝つ そうでない場合は ランダム なマスに 着手 する

基準となる ai2 との 対戦結果（単位は %）は以下の通りです。太字 は ai2 VS ai2 よりも 成績が良い 数値を表します。欠陥 の列は、アルゴリズム に 欠陥 があるため、ai2 との 対戦成績 が 良くても強い とは 限らない ことを表します。欠陥の詳細については、関数名のリンク先の説明を見て下さい。

関数名	o 勝	o 負	o 分	x 勝	x 負	x 分	勝	負	分	欠陥
ai1	78.1	17.5	4.4	44.7	51.6	3.8	61.4	34.5	4.1	あり
ai2	58.7	28.8	12.6	29.1	58.6	12.3	43.9	43.7	12.5
ai3	69.3	19.2	11.5	38.9	47.6	13.5	54.1	33.4	12.5
ai4	83.0	9.5	7.4	57.2	33.0	9.7	70.1	21.3	8.6	あり
ai5	81.3	11.9	6.8	52.2	39.4	8.5	66.8	25.6	7.6

ルールその 6（相手の勝利を阻止する）

弱い AI に対してどれだけ 大幅に有利 な AI を作成 しても 強い AI を 作った ことには なりません。例えば、じゃんけん で パーしか出さない AI は、じゃんけんで グーしか出さない AI に 100% 勝利 しますが、誰もそのような AI が 強いとは思わない でしょう。そのため、強い AI を 作成 する際には、対戦相手 として 強い AI を 想定 する必要があります。

前回の記事で、自分が 勝てる時 に 勝つ という ルール 5 が ある場合 と ない場合 では、ある場合のほう が 強くなる¹ ことを示しました。従って、対戦相手 として 強い AI を 想定 する場合は、自分だけ でなく、相手 も ルール 5 で着手する ことを 想定 する必要があります。

例えば、下図（数字 のマスは 空いているマス を表します）の 〇 の手番 の局面で、1 以外 のマスに 着手 を行うと、次 の 相手の手番 で × が 1 に 着手 を行うと × が勝利 するので、〇 が 次 の × の手番 で 負けない ようにするためには 必ず 1 に着手 する 必要 があります。

そこで、ルール 5 に、次の相手の手番 で 相手が勝つ ことが 可能 な 着手 を 行わない ルールを 加えた、下記の ルール 6 で ai6 を 実装 することにします。下記の 手順 2 を 別の言葉 で表現すると、「相手 が 勝利するマス に 自分で着手 して 邪魔 をする」のようになります。

1. 勝てるマス が 存在 すれば、そこに着手 する
2. そうでなければ、合法手 を 着手 した 局面 のうち、次 の 相手の手番 で、相手が着手 すると 相手が勝利 するマスが 存在すれば 、そこに着手 して 邪魔 をする
3. 上記のいずれでもなければ ランダム なマスに 着手 する

ルールの手順に関する注意点

上記の 手順 1 と 2 を 入れ替え ては いけない 点に 注意 して下さい。その理由は、勝てる場合 に 勝っておけば、相手の手番 が 来る ことは ない からです。例えば、下図の 〇 の手番 の局面で、上記の ルール 6 を適用 した場合は、2 のマスに 着手 して 〇 の勝利 になりますが、上記の 手順 1 と 2 を 入れ替えたルール では、次 の × 手番 で 1 に × が着手 すると × の勝利 になるので、1 に着手 してしまい、勝利を逃してしまう ことになります。

別の言葉で説明すると、ルール 6 の 手順 1 と 2 の 順番を入れ替えた場合 は、自分の勝ちより も、相手の勝利の邪魔 を 優先 することになります。

上記を 当たり前 だと 思う 人が いるかも しれませんが、ルールの数 が 多く なったり、ルール の 条件 が 複雑 な場合は、ルール の 手順 の 順番 を 正しく決める ことが 難しく なります。個々 の 手順 は 間違っていなくても、手順の順番 を 間違ってしまう と、間違ったルール になってしまうので、手順 の 順番 に 注意する必要 があることを忘れないで下さい。

ルール 6 の AI が、ルール 5 の AI よりも 強くなる ことは ほぼ自明 で、簡単に検証できる ので省略します。気になる方は、ルール 5 の検証 と同様に 表を書いて検証 してみて下さい。

合法手が 1 つしかない場合の処理

ルール 6 は、相手 の 勝利を阻止 することが 目的 ですが、合法手 が 1 つ しかない場合は、相手の手番 が 回ってこない ので、次の 相手の手番 を 考慮 する ルール 6 を 適用 することは できません。従って、ai6 の 先頭 に、下記 のプログラムを 記述する必要 があります。

• 4、5 行目：組み込み関数 len を使って、legal_moves の 要素の数 を 計算 することで、合法手の数 を 計算 し、その数 が 1 の場合は、legal_moves[0] を 返す

1  def ai6(mb_orig):
2      legal_moves = mb_orig.calc_legal_moves()
3      # 合法手が 1 つしかない場合は、その合法手を返り値として返す
4      if len(legal_moves) == 1:
5          return legal_moves[0]
6      # 以下、ルール 6 の処理を記述する

合法手 が 1 つ しかない場合は、5 行目に return legal_moves を 記述 すれば良いと 思う人 が いるかもしれません が、legal_moves は list なので、要素 が 1 つ しかない場合でも、その 要素を参照 する場合は、インデックス を 指定 して、return legal_moves[0] のように 記述する必要 がある点に 注意 して下さい。

上記の 4、5 行目 を 記述 することで、合法手 が 1 つ しかない場合は、ai6 は ルール 6 を 適用しない ことになります。従って、以後 の ルール 6 に関する 処理 では、説明がなくても、合法手 が 2 つ以上ある場合 の 処理を行う と考えて下さい。

前回の記事で説明したように、合法手 が 1 つ しかない場合は、どのような ルール であっても、選択 できる 合法手は同じ なので、合法手 が 1 つ しかない場合に ルール 6 を 適用 しても、 選択される合法手 は 常に同じ です。従って、本記事では省略しませんが、上記のプログラムの 4、5 行目 は 省略 することが できます。

ただし、前回の記事で説明したように、プログラムを修正 する際などで バグの原因 に なりやすい ので、意味がわからず に 省略 するのは 避けたほうが良い でしょう.

ルール 6 の実装方法

相手が勝利 できる マス は、以下 のような 条件のマス です。

• その マス が 相手 の 合法手（空いているマス）である
• その マスを含む 一直線上の 3 マスのうち、2 マス に 相手のマークが配置 されている ものがある

上記の条件 を 満たすマス を 探す プログラムを記述する方法は、それほど 簡単ではありません ので、今回の記事では、上記とは別 の、これまでに記述 したプログラムを うまく利用 できる、下記のような 考え方 で ルール 6 を 実装 することにします。なお、上記の条件 を満たすマスが あるかどうか を 判定 する 方法 については、今後の記事で紹介します。

• 自分の手番 で、着手 することで 勝利 できる 合法手 を 調べる処理 は ai5 で 実装済
• ということは、相手の手番 で、着手 することで 相手が勝利 できる 合法手 も 同様の方法 で 調べる ことが できる

ルール 6 のアルゴリズム

ルール 6 は、下記の アルゴリズム で 実装 することができます。下記のアルゴリズムのうち、手順 1、2、4 は、ルール 5 の アルゴリズム と 同じ です。異なる のは、手順 3 ですが、手順 1、2 と、手順 3-1、3-2 で行う 処理の内容 が、手番 が 自分と相手 で 異なる ことを 除けば、まったく同じ処理 を 行う ことに 注目 して下さい。

1. 現在の局面 の 合法手の一覧 から 順番 に 合法手 を 取り出し て 着手 を行う
2. 自分が勝利 する 合法手 があれば、それを採用 して 終了 する
3. 上記の 手順 1 で 着手 を行った それぞれの局面 に対して、下記の処理 を行う
   1. 合法手の一覧 から 順番 に 合法手 を 取り出し て 着手 を行う
   2. 相手が勝利 する 合法手 があれば、それを採用 して 終了 する
4. 上記の 手順 1 ~ 3 の 処理 が すべて終了 した時点で、自分が勝利 できる合法手も、相手が勝利 できる合法手も 存在しない ことが 確定 するので、ランダムな着手 を行う

わかりづらい と思った人のために、ルール 6 の アルゴリズム の 処理の実例 を紹介します。上記の説明の意味が良くわかった人はこの部分は飛ばしてもらっても構いません。

ルール 6 のアルゴリズムの処理の例 1

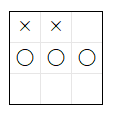
下図の場合の 処理の手順 を示します。図の 数字のマス は、空いているマス を表します。

• 手順 1、2 で、上図の 現在の局面 に対して、1 ~ 5 の 順 で 〇 の 着手 を行う
• 2 に着手 した時点で、〇 が勝利 するので、2 のマスを 採用 して 終了 する

採用 された 2 のマス に 〇 が 着手 することで、下図のように 〇 が勝利 します。

ルール 6 のアルゴリズムの処理の例 2

下図の場合の 処理の手順 を示します。

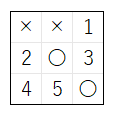
• 手順 1、2 で、上図の 現在の局面 に対して、1 ~ 5 の 順 で 〇 の 着手 を行う
• どのマス に 着手 を行っても 〇 は 勝利しない ので、手順 3 へ 進む
• 上図の 1 に 着手 した 下図の局面 に対して、下図の 2 ~ 5 の 順 で × の 着手 を行う。なお、図の 青いマス は、直前 に 着手 が行われた マス を表す

• どのマス に 着手 を行っても × は 勝利しない ので、現在の局面 の 2 に 着手 した 下図の局面 に対して、下図の 1、3 ~ 5 の 順 で × の 着手 を行う

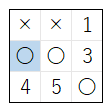
• 1 に着手 した時点で、× が勝利 するので、1 のマスを 採用 して 終了 する

採用 された 1 のマス に 〇 が 着手 することで、下図のように × の勝利 を 阻止 します。

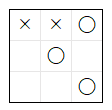
ルール 6 のアルゴリズムの処理の例 3

下図の場合の 処理の手順 を示します。

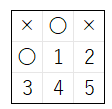
• 手順 1、2 で、上図の 現在の局面 に対して、1 ~ 5 の 順 で 〇 の 着手 を行う
• どのマス に 着手 を行っても 〇 は 勝利しない ので、手順 3 へ 進む
• 上図の 1 ~ 5 に 着手 した 下図 の それぞれの局面 に対して、順番 に、下図の それぞれ の空いている 1 ~ 5 の 順 で × の 着手 を行う

• すべての局面 で どのマス に 着手 を行っても × は 勝利しない ので 手順 3 が終了 する
• 手順 4 が実行され、現在の局面 の 1 ~ 5 の中から ランダムなマス を 採用 する

ai6 の実装

下記は、先程のアルゴリズムを再掲したものです。

1. 現在の局面 の 合法手の一覧 から 順番 に 合法手 を 取り出し て 着手 を行う
2. 自分が勝利 する 合法手 があれば、それを採用 して 終了 する
3. 上記の 手順 1 で 着手 を行った それぞれの局面 に対して、下記の処理 を行う
   1. 合法手の一覧 から 順番 に 合法手 を 取り出し て 着手 を行う
   2. 相手が勝利 する 合法手 があれば、それを採用 して 終了 する
4. 上記の 手順 1 の 繰り返しが終了 した時点で、自分が勝利 できる合法手も、相手が勝利 できる合法手も 存在しない ことが 確定 するので、ランダムな着手 を行う

先ほど説明したように、手順 1、2 と、手順 3-1、3-2 で行う 処理の内容 は、手番 が 自分と相手 で 異なる ことを 除けば、まったく同じ処理 を行うので、 ai6 は、下記のプログラムのように実装することができます。

• 6 ~ 15 行目：上記の 手順 1、2 の処理を行う部分で、この部分は、合法手 が 1 つ しかない場合の 8、9 行目 の 処理を除けば、ai5 と同じ
• 18 ~ 24 行目：18 行目 のプログラムが 実行 されるということは、元の局面 である mb_orig に対して、move に 着手 を行った mb の 局面 で、自分 が 勝利していない 場合である。その場合は、手順 3-1、3-2 の処理を、6 ~ 15 行目 と 同様の方法 で行う。6 ~ 15 行目 と、18 ~ 24 行目 の 違い は以下の通り
  • 合法手 が 1 つ しかない場合の 処理がない
  • mb_orig → mb
  • legal_moves → next_legal_moves
  • move → next_move
  • mb → next_mb

 1 from random import choice
 2 from copy import deepcopy
 3
 4  def ai6(mb_orig):
 5      # mb_orig の合法手の中で、自分が勝利できる合法手があればそこに着手する
 6      legal_moves = mb_orig.calc_legal_moves()
 7      # 合法手が 1 つしかない場合は、その合法手を返り値として返す
 8      if len(legal_moves) == 1:
 9         return legal_moves[0]
10      for move in legal_moves:
11          mb = deepcopy(mb_orig)
12          x, y = move
13          mb.move(x, y)
14          if mb.status == mb_orig.turn:
15              return move
16          # mb は、mb_orig に対して、move に着手を行った、相手の手番の局面
17          # mb の合法手の中で、相手が勝利できる合法手があればそこに着手して相手の勝利を阻止する
18          next_legal_moves = mb.calc_legal_moves()       
19          for next_move in next_legal_moves:
20              next_mb = deepcopy(mb)                
21              x, y = next_move
22              next_mb.move(x, y)
23              if next_mb.status == mb.turn:
24                  return next_move
25        
26      return choice(legal_moves)

行番号のないプログラム

from random import choice
from copy import deepcopy
 
def ai6(mb_orig):
    # mb_orig の合法手の中で、自分が勝利できる合法手があればそこに着手する
    legal_moves = mb_orig.calc_legal_moves()
    # 合法手が 1 つしかない場合は、その合法手を返り値として返す
    if len(legal_moves) == 1:
        return legal_moves[0]
    for move in legal_moves:
        mb = deepcopy(mb_orig)
        x, y = move
        mb.move(x, y)
        if mb.status == mb_orig.turn:
            return move
        # mb は、mb_orig に対して、move に着手を行った、相手の手番の局面
        # mb の合法手の中で、相手が勝利できる合法手があればそこに着手して相手の勝利を阻止する
        next_legal_moves = mb.calc_legal_moves()       
        for next_move in next_legal_moves:
            next_mb = deepcopy(mb)                
            x, y = next_move
            next_mb.move(x, y)
            if next_mb.status == mb.turn:
                return next_move
        
    return choice(legal_moves)

修正箇所

from random import choice
from copy import deepcopy

-def ai5(mb_orig):
+def ai6(mb_orig):
    # mb_orig の合法手の中で、自分が勝利できる合法手があればそこに着手する
    legal_moves = mb_orig.calc_legal_moves()
    # 合法手が 1 つしかない場合は、その合法手を返り値として返す
    if len(legal_moves) == 1:
        return legal_moves[0]
    for move in legal_moves:
        mb = deepcopy(mb_orig)
        x, y = move
        mb.move(x, y)
        if mb.status == mb_orig.turn:
            return move
        # mb は、mb_orig に対して、move に着手を行った、相手の手番の局面
        # mb の合法手の中で、相手が勝利できる合法手があればそこに着手して相手の勝利を阻止する
+       next_legal_moves = mb.calc_legal_moves()       
+       for next_move in next_legal_moves:
+           next_mb = deepcopy(mb)                
+           x, y = next_move
+           next_mb.move(x, y)
+           if next_mb.status == mb.turn:
+               return next_move
        
    return choice(legal_moves)

6 ~ 15 行目 と、18 ~ 24 行目 の 処理 は よく似ている ので、これまでのプログラムで行ってきたように、for 文 による 繰り返し処理 で まとめる ことができるように 思えるかもしれません が、18 ~ 24 行目 の処理は、6 行目の for 文の中 に 入れ子で記述 されているため、この 2 つの処理 を for 文 による 繰り返し処理 でうまく まとめる ことは 困難です。このような場合は、再起呼び出し という方法を使って まとめる ことが できます が、その方法については今後の記事で紹介します。

本当は、前回の記事のように、mb.play(ai=[ai6, ai2]) を 実行 して ai2 と 対戦 した 結果を表示 することで、ai6 を 正しく実装できているか どうかを 確認すべき なのですが、ルール が 複雑になる と、ランダムな着手 を行う ai2 と 対戦しても、なかなか ルール を 正しく実装できたこと を 確認できる局面 が 訪れない可能性が高く なります。そのような場合は、mb.play(ai=[ai6, None]) や、mb.play(ai=[None, ai6]) を実行して、自分 で ルール を 正しく実装できているか どうかを 確認できる ような 局面に誘導 して 確認する と良いでしょう。本記事では確認作業を省略しますが、気になる方 は 実際に確認 して下さい。

他の方法 として、実装した AI と 他の AI で 複数回対戦 し、意図通り の 成績 になることを 確認する ことで、正しく実装 できていると 推測する という方法もあります。ルール が 複雑 になって 確認が困難 な場合などで、この方法で 確認作業 を 代用 することがありますが、意図通りの成績 になっても、正しく実装 されているとは 限らない 点に 注意が必要 です。

ai2 との対戦

ai6 が 実装 できたので、下記のプログラムで、基準 となる ai2 と 対戦 します。なお、ai6 は、deepcopy や move メソッドを 何度も実行 する必要があるので、処理 に 時間 がかかります。そのため、筆者のパソコンでは処理に 約 80 秒 の時間が かかりました。

同じプログラム でも、コンピュータの CPU の性能、メモリの量、同時に実行 している アプリケーション など、さまざまな理由 で処理にかかる 時間 は 異なり ます。

from ai import ai_match, ai2, ai3, ai4, ai5

ai_match(ai=[ai6, ai2])

実行結果（実行結果はランダムなので下記とは異なる場合があります）

ai6 VS ai2
count     win    lose    draw
o        8797     147    1056
x        6772     675    2553
total   15569     822    3609

ratio     win    lose    draw
o       88.0%    1.5%   10.6%
x       67.7%    6.8%   25.5%
total   77.8%    4.1%   18.0%

80 秒 は 長い ので、下記のプログラムのように、1000 回 の 対戦 を行ってみました。実行 には 10000 回の 1/10 の 約 8 秒 かかりましたが、10000 回 の 対戦結果 と 比較 して ほとんど 結果は 変わらない ので 1000 回 でも 問題はない でしょう。以前の記事では 1 分で行える回数としましたが、今後 は時間がかかる場合は、1000 回 で 対戦を行う ことにします。

ai_match(ai=[ai6, ai2], match_num=1000)

実行結果（実行結果はランダムなので下記とは異なる場合があります）

ai6 VS ai2
count     win    lose    draw
o         876      16     108
x         679      58     263
total    1555      74     371

ratio     win    lose    draw
o       87.6%    1.6%   10.8%
x       67.9%    5.8%   26.3%
total   77.8%    3.7%   18.6%

下記は、上記の結果（10000 回のほう）を表に加えたものです。

関数名	o 勝	o 負	o 分	x 勝	x 負	x 分	勝	負	分	欠陥
ai1	78.1	17.5	4.4	44.7	51.6	3.8	61.4	34.5	4.1	あり
ai2	58.7	28.8	12.6	29.1	58.6	12.3	43.9	43.7	12.5
ai3	69.3	19.2	11.5	38.9	47.6	13.5	54.1	33.4	12.5
ai4	83.0	9.5	7.4	57.2	33.0	9.7	70.1	21.3	8.6	あり
ai5	81.2	12.3	6.5	51.8	39.8	8.4	66.5	26.0	7.4
ai6	88.0	1.5	10.6	67.7	6.8	25.5	77.8	4.1	18.0

表から、ai6 は、他の どの AI より も 基準 となる ai2 に 対して 強い ことがわかります。また、〇 を担当 した場合、× を担当 した場合、通算 の場合の 敗率 は いずれも 7 % 以下 なので、相手の勝利 を 阻止 する ルール 6 の 効果 が表れていることが 確認 できます。

ルール 6 で負ける場合がある理由

相手の勝利 を 阻止 する ルール なのに、負ける場合がある 点について疑問に思った方がいるかもしれません。そのような方は、負ける場合がある 理由について少し考えてみて下さい。

具体的には、以下の 2 つの条件 を満たす 局面 では、ルール 6 でも 負ける ことになります。

• 下図のように、どのマスに着手しても 自分 が 勝つことができない
• 下図の 黄色のマス のように、次の手番で 相手が勝利できる マスが 2 つ以上 ある

下図では、片方のマス しか 邪魔 を できない ので、相手の勝利 を 阻止できません。

なお、上記 のような 局面 になってしまった場合は、ルール 6 に限らず、どのようなルール を使っても 相手の勝利 を 阻止 することは 不可能 です。

ai6 のバグの修正

プログラミングに 慣れている方 は既に 気がづいているかも しれませんが、実は ai6 には、ルール 6 を 正しく実装できていない という バグ があります。正直に言うと、筆者は、最初は 正しいつもり で上記の ai6 を 実装 し、後からバグ がある事に 気が付きました。ルール 6 と、ai6 のプログラムを 見比べて、どこが間違っているかについて考えてみて下さい。

なお、上記で バグのある ai6 で ai2 と 対戦を行った のは、バグを修正 することで、ai6 VS ai2 の 成績 が 向上する ことを 示したい からです。

バグの原因

下記は、先程のアルゴリズムを再掲したものです。

1. 現在の局面 の 合法手の一覧 から 順番 に 合法手 を 取り出し て 着手 を行う
2. 自分が勝利 する 合法手 があれば、それを採用 して 終了 する
3. 上記の 手順 1 で 着手 を行った それぞれの局面 に対して、下記の処理 を行う
   1. 合法手の一覧 から 順番 に 合法手 を 取り出し て 着手 を行う
   2. 相手が勝利 する 合法手 があれば、それを採用 して 終了 する
4. 上記の 手順 1 の 繰り返しが終了 した時点で、自分が勝利 できる合法手も、相手が勝利 できる合法手も 存在しない ことが 確定 するので、ランダムな着手 を行う

バグの 原因 は、ai6 が、手順 2 を 正しく実装していない 点にあります。

上記の 手順 2 の「自分が勝利 する 合法手 があれば、それを採用 して 終了 する」は、合法手 を すべて調べた結果 の事を表しています。従って、手順 3 は、手順 1、2 の処理が 完了 した 後で 行う必要があります。しかし、ai6 では、合法手 を すべて調べた後ではなく、合法手を 一つ調べるたび に、手順 3 の処理 を行っています。

この違い が どのように影響 するかを、下図の局面 で 説明 します。

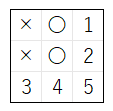
ルール 6 のアルゴリズムの処理を正しく行った場合

• 手順 1、2 で、上図の 最初の局面 に対して、1 ~ 5 の 順 で 〇 の 着手 を行う
• 4 に着手 した時点で、〇 が勝利 するので、4 のマスを 採用 して 終了 する

採用 された 4 のマス に 〇 が 着手 することで、下図のように 〇 が勝利 します。

ルール 6 のアルゴリズムを間違って実装した ai6 の場合

• 手順 1、2 で、上図の 最初の局面 に対して、1 ~ 5 の 順 で 〇 の 着手 を行う
• 1 に 着手 した場合、下図のように、〇 は 勝利していない。ai6 は 手順 1、2 の処理が すべて終了する前 に、下図の局面 で、手順 3 の 処理 を行う（この処理が間違い）

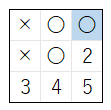
• 上図で、3 に着手 した時点で、× が勝利 するので、3 のマスを 採用 して 終了 する

採用 された 3 のマス に 〇 が 着手 することで、下図のように × の勝利 を 阻止 します。

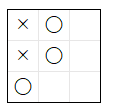
上記のように、間違った処理 を行う ai6 は、〇 の勝利 を 逃す 結果になります。

ai6 のバグの内容

上記から、ai6 の バグ を 言葉で表現 すると、以下のようになります。

以下の 2 つの条件 が 同時に満たされる局面 で、自分が勝利せず に 相手の勝利を阻止 してしまう 場合がある

• 自分の着手 で 自分が勝利 できる 合法手 が ある
• いずれか の 自分の着手 の 後 の 相手の着手 で、相手が勝利 できる 合法手 が ある

ai6 の修正

バグの 原因 は、手順 1、2 の処理を すべて行う前 に 手順 3 を行う ことにあります。そこで、手順 1、2 の 処理 を 先に行ってから、手順 3 の 処理を行う ようにすることで、ai6 の バグを修正 することができます。また、手順 3 の 処理 は、自分が勝利 する 合法手 が 存在しない 場合に 行う処理 です。従って、手順 3 は、下記のプログラムのように、修正前 の ai6 のプログラムから、手順 2 の 処理 を 削除 したプログラムで 記述 できます。

• 7 ~ 12 行目：この 繰り返し処理 の中で、手順 1、2 の処理 のみを行う ように 修正 する
• 14 ~ 26 行目：元 の ai6 の 繰り返し処理 の中から、手順 2 の「自分が勝利 する 合法手 があれば、それを採用 して 終了 する」処理 を 削除 したプログラムを 記述 する

14 ~ 26 行目 のプログラムが、修正前 の ai6 のプログラムから、手順 2 の 処理 を行う、下記の 11、12 行目 のプログラムを 削除 したものと 同じ であることを 確認 して下さい。

 1  def ai6(mb_orig):
 2      # mb_orig の合法手の中で、自分が勝利できる合法手があればそこに着手する
 3      legal_moves = mb_orig.calc_legal_moves()
 4      # 合法手が 1 つしかない場合は、その合法手を返り値として返す
 5      if len(legal_moves) == 1:
 6          return legal_moves[0]
 7      for move in legal_moves:
 8          mb = deepcopy(mb_orig)
 9          x, y = move
10          mb.move(x, y)
11          if mb.status == mb_orig.turn:
12              return move
13      # 〇 が勝利する合法手が存在しないことが確定したので、手順 3 を行う
14      for move in legal_moves:
15          mb = deepcopy(mb_orig)
16          x, y = move
17          mb.move(x, y)
18          # mb は、mb_orig に対して、move に着手を行った、相手の手番の局面
19          # mb の合法手の中で、相手が勝利できる合法手があればそこに着手して相手の勝利を阻止する
20          next_legal_moves = mb.calc_legal_moves()       
21          for next_move in next_legal_moves:
22              next_mb = deepcopy(mb)                
23              x, y = next_move
24              next_mb.move(x, y)
25              if next_mb.status == mb.turn:
26                  return next_move
27        
28      return choice(legal_moves)

行番号のないプログラム

def ai6(mb_orig):
    # mb_orig の合法手の中で、自分が勝利できる合法手があればそこに着手する
    legal_moves = mb_orig.calc_legal_moves()
    # 合法手が 1 つしかない場合は、その合法手を返り値として返す
    if len(legal_moves) == 1:
        return legal_moves[0]
    for move in legal_moves:
        mb = deepcopy(mb_orig)
        x, y = move
        mb.move(x, y)
        if mb.status == mb_orig.turn:
            return move
    # 〇 が勝利する合法手が存在しないことが確定したので、手順 3 を行う
    for move in legal_moves:
        mb = deepcopy(mb_orig)
        x, y = move
        mb.move(x, y)
        # mb は、mb_orig に対して、move に着手を行った、相手の手番の局面
        # mb の合法手の中で、相手が勝利できる合法手があればそこに着手して相手の勝利を阻止する
        next_legal_moves = mb.calc_legal_moves()       
        for next_move in next_legal_moves:
            next_mb = deepcopy(mb)                
            x, y = next_move
            next_mb.move(x, y)
            if next_mb.status == mb.turn:
                return next_move
        
    return choice(legal_moves)

修正箇所

def ai6(mb_orig):
    # mb_orig の合法手の中で、自分が勝利できる合法手があればそこに着手する
    legal_moves = mb_orig.calc_legal_moves()
    # 合法手が 1 つしかない場合は、その合法手を返り値として返す
    if len(legal_moves) == 1:
        return legal_moves[0]
    for move in legal_moves:
        mb = deepcopy(mb_orig)
        x, y = move
        mb.move(x, y)
        if mb.status == mb_orig.turn:
            return move
    # 〇 が勝利する合法手が存在しないことが確定したので、手順 3 を行う
+   for move in legal_moves:
+       mb = deepcopy(mb_orig)
+       x, y = move
+       mb.move(x, y)
        # mb は、mb_orig に対して、move に着手を行った、相手の手番の局面
        # mb の合法手の中で、相手が勝利できる合法手があればそこに着手して相手の勝利を阻止する
        next_legal_moves = mb.calc_legal_moves()       
        for next_move in next_legal_moves:
            next_mb = deepcopy(mb)                
            x, y = next_move
            next_mb.move(x, y)
            if next_mb.status == mb.turn:
                return next_move
        
    return choice(legal_moves)

修正後の ai6 と ai2 の対戦

修正後 の ai6 で、ai2 と改めて 対戦 を行うことにします。

ai_match(ai=[ai6, ai2], match_num=1000)

実行結果（実行結果はランダムなので下記とは異なる場合があります）

ai6 VS ai2
count     win    lose    draw
o         889      22      89
x         703      62     235
total    1592      84     324

ratio     win    lose    draw
o       88.9%    2.2%    8.9%
x       70.3%    6.2%   23.5%
total   79.6%    4.2%   16.2%

下記は、修正前 と 修正後 の ai6 と、ai2 で 対戦 した場合の 成績 を表にしたものです。

関数名	o 勝	o 負	o 分	x 勝	x 負	x 分	勝	負	分	欠陥
ai6 前	88.0	1.5	10.6	67.7	6.8	25.5	77.8	4.1	18.0	あり
ai6 後	88.9	2.2	8.9	70.3	6.2	23.5	79.6	4.2	16.2

表から、バグを修正 した 結果、すべての場合で 勝率 が 2% 程 することがわかります。

なお、成績 が ほんの少し しか 向上 しない理由の検証は省略しますが、おそらく バグ が 勝敗に影響 するような 局面 が ほとんど出現しない からだと思います。興味と余裕がある方は、実際に検証してみて下さい。

ai6 の改良 その 1（重複する処理を省く）

下記は、先程修正した ai6 の 一部 を 抜粋 したプログラムです。よく見ると、2 ~ 5 行目 と、9 ~ 12 行目 で 全く同じ処理 が 記述 されているため、同じ処理 を 2 度行う という 無駄 が生じています。また、その部分で行われる deepcopy による データの深いコピー や、move メソッドで 勝敗判定 を行う 処理 は、それなりに 時間がかかる ので、そのような処理を 2 回 も 行う ことで、プログラムの 処理 に、余計な時間 がかかってしまいます。

実際に 筆者のパソコン で ai_match(ai=[ai6, ai6], match_num=1000) を実行すると、同じ処理 を 2 回行わない がバグのある 修正前 では 8.4 秒、修正後 では 9.4 秒 かかりました。

 1  def ai6(mb_orig):
略
 2      for move in legal_moves:
 3          mb = deepcopy(mb_orig)
 4          x, y = move
 5          mb.move(x, y)
 6          if mb.status == mb_orig.turn:
 7              return move
 8      # 〇 が勝利する合法手が存在しないことが確定したので、手順 3 を行う
 9      for move in legal_moves:
10          mb = deepcopy(mb_orig)
11          x, y = move
12          mb.move(x, y)
略

改良の方法

上記のプログラムの 2 行目 の 繰り返し処理 と、9 行目 の 繰り返し処理 には、同一 の for move in legal_moves: という 記述 が行われています。また、2 ~ 7 行目 の 処理 を 実行 しても繰り返し処理の 反復可能オブジェクト に記述されている legal_moves の 値 は 変化しない ので、2 行目 と 9 行目 の 繰り返し処理 では、どちらも 同じ値 が 順番 に legal_moves から 取り出され て move に代入 されます。

それぞれ の for 文 の ブロック の 3 ~ 5 行目 と、10 ~ 12 行目 では 同一の処理 が行われるので、2 行目 の for 文 の ブロック の 5 行目 の処理で 計算 される mb の値 と、9 行目 の for 文 の ブロック の 12 行目 の処理で 計算 される mb の値 は、move に代入された値が 同じであれば、必ず 同じ内容 になります。

上記から、2 行目 の for 文 の n 回目 の繰り返し処理の 5 行目 で計算される mb と、9 行目 の for 文 の n 回目 の繰り返し処理の 12 行目 で計算される mb の値は、同じ内容 になります。従って、5 行目 で 計算 した mb を list に 記録 しておくことで、10 ~ 12 行目 の処理を行う代わりに、記録した list から 対応するデータ を 取り出して利用 することができます。

別の言葉で説明すると、手順 3 で 必要となる、「現在の局面 に対して それぞれ の 合法手 を 着手 した 局面」 は、手順 1、2 の 処理 を行う際に、計算する ので、その時 にそれらの 局面 を list に記録 しておき、手順 3 で 再利用できる ということです。

改良版の ai6 の実装

下記は、そのような処理を行うように ai6 を 改良 したプログラムです。

• 7 行目：8 行目 の for 文 の 繰り返し処理 の中の 11 行目 で 計算 した mb を 記録 するための list を 代入 する mb_list を、空の list で 初期化 する
• 12 行目：mb_list の 要素 に mb を追加 して 記録 する
• 16 行目：元の for 文の代わりに、mb_list から 順番 に 要素 を 取り出し、mb に代入するという、for 文 による 繰り返し処理 を行う。この 16 行目 の 処理 で、先程の 改良前 の 9 ~ 12 行目 と 同じ処理 が行われる（そのことは、下記の 修正箇所 で 確認できる）

 1  def ai6(mb_orig):
 2      # mb_orig の合法手の中で、自分が勝利できる合法手があればそこに着手する
 3      legal_moves = mb_orig.calc_legal_moves()
 4      # 合法手が 1 つしかない場合は、その合法手を返り値として返す
 5      if len(legal_moves) == 1:
 6          return legal_moves[0]
 7      mb_list = []
 8      for move in legal_moves:
 9          mb = deepcopy(mb_orig)
10          x, y = move
11          mb.move(x, y)
12          mb_list.append(mb)
13          if mb.status == mb_orig.turn:
14              return move
15      # 〇 が勝利する合法手が存在しないことが確定したので、手順 3 を行う
16      for mb in mb_list:
17          # mb は、mb_orig に対して、move に着手を行った、相手の手番の局面
18          # mb の合法手の中で、相手が勝利できる合法手があればそこに着手して相手の勝利を阻止する
19          next_legal_moves = mb.calc_legal_moves()       
20          for next_move in next_legal_moves:
21              next_mb = deepcopy(mb)                
22              x, y = next_move
23              next_mb.move(x, y)
24              if next_mb.status == mb.turn:
25                  return next_move
26        
27      return choice(legal_moves)

行番号のないプログラム

def ai6(mb_orig):
    # mb_orig の合法手の中で、自分が勝利できる合法手があればそこに着手する
    legal_moves = mb_orig.calc_legal_moves()
    # 合法手が 1 つしかない場合は、その合法手を返り値として返す
    if len(legal_moves) == 1:
        return legal_moves[0]
    mb_list = []
    for move in legal_moves:
        mb = deepcopy(mb_orig)
        x, y = move
        mb.move(x, y)
        mb_list.append(mb)
        if mb.status == mb_orig.turn:
            return move
    # 〇 が勝利する合法手が存在しないことが確定したので、手順 3 を行う
    for mb in mb_list:
        # mb は、mb_orig に対して、move に着手を行った、相手の手番の局面
        # mb の合法手の中で、相手が勝利できる合法手があればそこに着手して相手の勝利を阻止する
        next_legal_moves = mb.calc_legal_moves()       
        for next_move in next_legal_moves:
            next_mb = deepcopy(mb)                
            x, y = next_move
            next_mb.move(x, y)
            if next_mb.status == mb.turn:
                return next_move
        
    return choice(legal_moves)

修正箇所

def ai6(mb_orig):
    # mb_orig の合法手の中で、自分が勝利できる合法手があればそこに着手する
    legal_moves = mb_orig.calc_legal_moves()
    # 合法手が 1 つしかない場合は、その合法手を返り値として返す
    if len(legal_moves) == 1:
        return legal_moves[0]
+   mb_list = []
    for move in legal_moves:
        mb = deepcopy(mb_orig)
        x, y = move
        mb.move(x, y)
+       mb_list.append(mb)
        if mb.status == mb_orig.turn:
            return move
    # 〇 が勝利する合法手が存在しないことが確定したので、手順 3 を行う
-   for move in legal_moves:
-       mb = deepcopy(mb_orig)
-       x, y = move
-       mb.move(x, y)
+   for mb in mb_list:
        # mb は、mb_orig に対して、move に着手を行った、相手の手番の局面
        # mb の合法手の中で、相手が勝利できる合法手があればそこに着手して相手の勝利を阻止する
        next_legal_moves = mb.calc_legal_moves()       
        for next_move in next_legal_moves:
            next_mb = deepcopy(mb)                
            x, y = next_move
            next_mb.move(x, y)
            if next_mb.status == mb.turn:
                return next_move
        
    return choice(legal_moves)

下記は、改良後 に ai6 VS ai2 に 対戦 を行うプログラムです。実行結果 は 修正前 と ほぼ同じ ですが、処理時間 は、筆者のパソコンでは 9.4 秒 から 8.5 秒 に短縮されました。

ai_match(ai=[ai6, ai2], match_num=1000)

実行結果（実行結果はランダムなので下記とは異なる場合があります）

ai6 VS ai2
count     win    lose    draw
o         896      15      89
x         702      60     238
total    1598      75     327

ratio     win    lose    draw
o       89.6%    1.5%    8.9%
x       70.2%    6.0%   23.8%
total   79.9%    3.8%   16.4%

ai6 の改良 その 2（アルゴリズムの改良）

下記は ルール 6 の アルゴリズム を 再掲 したものです。実は、下記の アルゴリズム を、より 効率の良い ものに 改良 することが できます。その方法について少し考えてみて下さい。

1. 現在の局面 の 合法手の一覧 から 順番 に 合法手 を 取り出し て 着手 を行う
2. 自分が勝利 する 合法手 があれば、それを採用 して 終了 する
3. 上記の 手順 1 で 着手 を行った それぞれの局面 に対して、下記の処理 を行う
   1. 合法手の一覧 から 順番 に 合法手 を 取り出し て 着手 を行う
   2. 相手が勝利 する 合法手 があれば、それを採用 して 終了 する
4. 上記の 手順 1 の 繰り返しが終了 した時点で、自分が勝利 できる合法手も、相手が勝利 できる合法手も 存在しない ことが 確定 するので、ランダムな着手 を行う

上記の アルゴリズム の 手順 3 では、現在の局面 に対して、合法手 を 着手 した それぞれ の 局面 に対して、相手の合法手 を すべて着手 しています。そのため、例えば 現在の局面 の 合法手 が n 通り だった場合、最大² で n * (n - 1) 通り³ の 着手 を行う必要があります。

理由はこの後で詳しく説明しますが、手順 3 は、下記のような 効率のよい アルゴリズムに 置き換える ことができます。

3. 現在の局面 を 相手の手番 と みなす
　　1. 現在の局面 の 合法手の一覧 から 順番 に 合法手 を 取り出し て 着手 を行う
　　2. 相手が勝利 する 合法手 があれば、それを採用 して 終了 する

このアルゴリズムであれば、例えば 現在の局面 の 合法手 が n 通り だった場合、最大 で n 通り しか 着手 を行う 必要がなくなる ので、処理の時間 を 短縮 することができます。

下記の表は 合法手の数 と、それぞれのアルゴリズムで必要となる 着手の数 の 最大値 です。表から、合法手 の数が 多いほど、必要な 着手 の 最大値 を 大幅に減らす ことができることが分かります。また、〇× ゲーム は、最初 の 合法手 の数が 9 で、1 手ごと に合法手の数が 1 ずつ減る ので、表の 合計 を計算することで 1 試合当たり で必要となる 着手の計算回数 の 最大値 を 見積もる ことができます。表から 改良版のアルゴリズム では、合計 が 約 1/5 になるので、かなりの 計算時間 の 削減 を 期待 できるでしょう。

合法手の数	2	3	4	5	6	7	8	9	合計
元のアルゴリズム	2	6	12	20	30	42	56	72	240
改良版のアルゴリズム	2	3	4	5	6	7	8	9	44

上記は 概算 に すぎない ので、正確ではない 点に 注意 して下さい。例えば、上記の計算では、ゲームが 8 手以内 で 決着 する場合を 考慮していません。

上記のアルゴリズムが 正しい理由 について少し考えてみて下さい。

改良版のアルゴリズムが正しい理由

〇× ゲーム は 下記の性質 があるゲームです。

• 一度 マークを配置したマス は、その 内容が変更される ことは 決してない
• 一度の 手番 で自分の マークを配置できるマス は 1 マスだけ である
• 自分と相手の 手番 は 交互に回ってくる

上記の性質 から、自分の手番 の 局面 の 合法手 に、次 の 相手の手番 で 相手が着手 することで 相手が勝利するか どうかは、以下の場合を除いて変化 することは ありません。

1. 自分の着手 で 自分が勝利 する（相手の手番 が 回ってこない）
2. 自分 がそのマスに 着手する（相手 がそのマスに 着手できない）

例えば、下図 の 局面 で、〇 が 2 に着手 すると 〇 が勝利 し、1 に着手 すると 次 の 相手の × の手番 で × は 1 に着手できません が、それ以外 の どの合法手 に 〇 が着手 しても、1 に × が着手 して × が勝利 します。

手順 3 の処理を 実行 するということは、現在の局面 で 〇 がどの 合法手に着手 しても 勝利できない ことが 確定 したということなので、上記の 条件 1 が 満たされる ことは ありません。また、手順 3 の 意図 は、相手 がそのマスに 着手 することで、相手が勝利するか どうかを 調べる ことなので、上記の 条件 2 は 考慮 に入れる 必要 は ありません。

従って、改良前 の 手順 3 の 処理 を行う際に、自分は上記の 条件 1、2 以外 の合法手に 着手した局面 で、相手 が 勝利できるか どうかを 判定 しますが、先ほど説明したように、条件 1、2 以外 のマスに 着手 を行った場合は、相手の着手 による 勝利 に 影響 を 与えません。

改良前 の 手順 3 で、自分の着手 が、相手の着手 による 勝利 に 影響を与えない ということは、自分 が 着手しない場合 でも 相手の勝利 に 影響を与えない ということなので、手順 3 で、現在の局面 を 相手の手番 と考えても 相手の勝利 を 調べる ことが できます。以上が、改良 した アルゴリズム 3 によって、ルール 6 の 処理 を行うことができる 理由 です。

具体例による説明

言葉の説明だけでは わかりづらい と思いますので、具体例 を挙げて 説明 します。

下図の局面 で、次 の 相手の × の手番 で、相手 が 1 に 着手 した場合に、× が勝利するか どうかを 判定 することを考えてみて下さい。

この局面 では、〇 は 合法手 の 1 ~ 5 のどのマスに 着手 しても 勝利できず、手順 1、2 で 処理 が 終了 することは ない ので、手順 3 の処理が 行われます。

手順 3 では、上図の局面 で、1 ~ 5 の それぞれ のマスに 〇 が着手 を行った 下図 の それぞれの局面 で、× が勝利 できる 合法手 が あるかどうか を調べます。

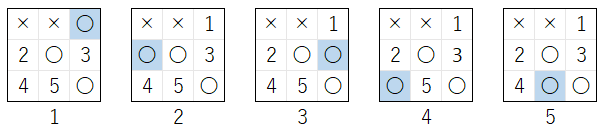
次に、手順 3 で × が 1 のマスに 着手 して 勝利できるか どうかを どのように判定 しているかを考えてみて下さい。

手順 3 では、上図の 2 ~ 4 の 局面 で、実際 に 1 のマスに × が着手 を行った、下図の 2 ~ 4 の 局面 の状態を 調べる ことで、その 判定 を行います。しかし、下図 からわかるように、現在の局面 で、〇 が 1 以外 の 2 ~ 4 のどのマスに 着手 を行っても、その 次 の × の手番 で × が 1 に 着手 を行うと × が勝利します。

このようなことが起きるのは、先ほど説明した 〇× ゲームの性質 が 原因 です。

〇 が 1 以外 のどの合法手に 着手 しても × の勝利 に 影響を与えない ということは、〇 の 着手 が、× の 勝利 に 影響しない という事を意味します。従って、下図の「着手なし」のように、現在の局面 で 〇 が 着手を行わず に × が 1 に着手 を行っても、× が勝利 します。

上記は、× が着手 することで × が勝利 する 1 のマス についての説明ですが、着手 しても × が勝利しない、2 ~ 4 のマスについても、同様の理由 で、現在の局面 で 〇 が 着手を行わなくても、× が勝利しない という 結果 に 影響 を与えることは ありません。気になる方は、上記のような 図 を書いて 確認 してみて下さい。

上記の事から、手順 3 の 処理 で、〇 が 着手を行う必要がない、すなわち、現在の局面 を 相手の手番 の局面と みなして 処理を行っても 良い ことがわかります。

改良版のアルゴリズムを使った ai6 の実装

下記のプログラムは、改良版 のアルゴリズムで ai6 を 実装 したプログラムです。

• mb_list に関する 処理 は 必要が無くなった ので 削除 した
• 16 行目：legal_moves に対する 繰り返し処理 を行うように 修正 する
• 18 行目：mb の 手番 を 入れ替える
• 19 行目：入れ替えた手番 を enemy_turn に 代入 して とっておく
• 20、21 行目：相手の手番 で 合法手 に 着手 を行う
• 22、23 行目：相手が勝利 していた場合は、その 合法手 を 返り値 として 返す

なお、元のプログラム では、相手の手番 の 局面 を表す mb を コピー した mb_next に対して 着手 を行っていたので、22 行目では 相手の手番 を mb.turn のように 記述 できました。一方、改良版 では mb に対して 着手 を行うので、mb.turn は 自分の手番 になります。そのため、19 行目 で 相手の手番 を enemy_turn に 代入 して 記録 しておく 必要 があります。

 1  from marubatsu import Marubatsu
 2 
 3  def ai6(mb_orig):
 4      # mb_orig の合法手の中で、自分が勝利できる合法手があればそこに着手する
 5      legal_moves = mb_orig.calc_legal_moves()
 6      # 合法手が 1 つしかない場合は、その合法手を返り値として返す
 7      if len(legal_moves) == 1:
 8          return legal_moves[0]
 9      for move in legal_moves:
10          mb = deepcopy(mb_orig)
11          x, y = move
12          mb.move(x, y)
13          if mb.status == mb_orig.turn:
14              return move
15      # 〇 が勝利する合法手が存在しないことが確定したので、手順 3 を行う
16      for move in legal_moves:
17          mb = deepcopy(mb_orig)
18          mb.turn = Marubatsu.CROSS if mb.turn == Marubatsu.CIRCLE else Marubatsu.CIRCLE
19          enemy_turn = mb.turn
20          x, y = move
21          mb.move(x, y)
22          if mb.status == enemy_turn:
23              return move
24       
25      return choice(legal_moves)

行番号のないプログラム

from marubatsu import Marubatsu

def ai6(mb_orig):
    # mb_orig の合法手の中で、自分が勝利できる合法手があればそこに着手する
    legal_moves = mb_orig.calc_legal_moves()
    # 合法手が 1 つしかない場合は、その合法手を返り値として返す
    if len(legal_moves) == 1:
        return legal_moves[0]
    for move in legal_moves:
        mb = deepcopy(mb_orig)
        x, y = move
        mb.move(x, y)
        if mb.status == mb_orig.turn:
            return move
    # 〇 が勝利する合法手が存在しないことが確定したので、手順 3 を行う
    for move in legal_moves:
        mb = deepcopy(mb_orig)
        mb.turn = Marubatsu.CROSS if mb.turn == Marubatsu.CIRCLE else Marubatsu.CIRCLE
        enemy_turn = mb.turn
        x, y = move
        mb.move(x, y)
        if mb.status == enemy_turn:
            return move
       
    return choice(legal_moves)

修正箇所

from marubatsu import Marubatsu

def ai6(mb_orig):
    # mb_orig の合法手の中で、自分が勝利できる合法手があればそこに着手する
    legal_moves = mb_orig.calc_legal_moves()
    # 合法手が 1 つしかない場合は、その合法手を返り値として返す
    if len(legal_moves) == 1:
        return legal_moves[0]
-   mb_list = []
    for move in legal_moves:
        mb = deepcopy(mb_orig)
        x, y = move
        mb.move(x, y)
-       mb_list.append(mb)
        if mb.status == mb_orig.turn:
            return move
    # 〇 が勝利する合法手が存在しないことが確定したので、手順 3 を行う
-   for mb in mb_list:
+   for move in legal_moves:
-       # mb は、mb_orig に対して、move に着手を行った、相手の手番の局面
-       # mb の合法手の中で、相手が勝利できる合法手があればそこに着手して相手の勝利を阻止する
-       next_legal_moves = mb.calc_legal_moves()       
-       for next_move in next_legal_moves:
-           next_mb = deepcopy(mb)                
-           x, y = next_move
-           next_mb.move(x, y)
-           if next_mb.status == mb.turn:
-               return next_move
+       mb = deepcopy(mb_orig)
+       mb.turn = Marubatsu.CROSS if mb.turn == Marubatsu.CIRCLE else Marubatsu.CIRCLE
+       enemy_turn = mb.turn
+       x, y = move
+       mb.move(x, y)
+       if mb.status == enemy_turn:
+           return move
       
    return choice(legal_moves)

下記は、修正後 の ai6 と ai2 で 対戦 を行うプログラムです。実行結果 は 修正前 と ほぼ同じ ですが、処理時間 は、筆者のパソコンでは 8.5 秒 から 2.8 秒 に、大幅に短縮 されました。これは、約 1/3 の 短縮 なので、先程 の 概算 の 1/5 ほどは 短縮されていません が、実際に アルゴリズムの改良 によって 処理時間 を かなり短縮 できることが 確認 できました。

このように、同じ処理 を行う場合でも、アルゴリズム によって、処理の速度 が 大きく変わる 場合があります。ただし、初心者の方が、今回の記事で紹介したようなアルゴリズムを自分で考えるのは難しいでしょう。自分 で 効率の良いアルゴリズム を 考える ためには、さまざまなアルゴリズム を 体験 して 勉強 する 必要 があります。本記事でさまざなアルゴリズムを紹介しているのはそのためです。

実行時間が短縮されたので、以後 は 10000 回 の 対戦を行う ことにします。

ai_match(ai=[ai6, ai2], match_num=1000)

実行結果（実行結果はランダムなので下記とは異なる場合があります）

ai6 VS ai2
count     win    lose    draw
o         896      17      87
x         692      56     252
total    1588      73     339

ratio     win    lose    draw
o       89.6%    1.7%    8.7%
x       69.2%    5.6%   25.2%
total   79.4%    3.6%   17.0%

他の AI との対戦

他の ai3、ai4、ai5、と自分自身と対戦してみます。

ai_match(ai=[ai6, ai3])

実行結果（実行結果はランダムなので下記とは異なる場合があります）

ai6 VS ai3
count     win    lose    draw
o        8685     147    1168
x        6193     577    3230
total   14878     724    4398

ratio     win    lose    draw
o       86.9%    1.5%   11.7%
x       61.9%    5.8%   32.3%
total   74.4%    3.6%   22.0%

ai_match(ai=[ai6, ai4])

実行結果（実行結果はランダムなので下記とは異なる場合があります）

ai6 VS ai4
count     win    lose    draw
o        9240     373     387
x        6615    2903     482
total   15855    3276     869

ratio     win    lose    draw
o       92.4%    3.7%    3.9%
x       66.1%   29.0%    4.8%
total   79.3%   16.4%    4.3%

ai_match(ai=[ai6, ai5])

実行結果（実行結果はランダムなので下記とは異なる場合があります）

ai6 VS ai5
count     win    lose    draw
o        8878     228     894
x        6549    1372    2079
total   15427    1600    2973

ratio     win    lose    draw
o       88.8%    2.3%    8.9%
x       65.5%   13.7%   20.8%
total   77.1%    8.0%   14.9%

ai_match(ai=[ai6, ai6])

実行結果（実行結果はランダムなので下記とは異なる場合があります）

ai6 VS ai6
count     win    lose    draw
o        3091    1693    5216
x        1765    3127    5108
total    4856    4820   10324

ratio     win    lose    draw
o       30.9%   16.9%   52.2%
x       17.6%   31.3%   51.1%
total   24.3%   24.1%   51.6%

下記は、上記の結果を表にまとめたものです。

関数名	o 勝	o 負	o 分	x 勝	x 負	x 分	勝	負	分
ai6 VS ai2	88.9	2.2	8.9	70.3	6.2	23.5	79.6	4.2	16.2
ai6 VS ai3	86.9	1.5	11.7	61.9	5.8	32.3	74.4	3.6	22.0
ai6 VS ai4	92.4	3.7	3.9	66.1	29.0	4.8	79.3	16.4	4.3
ai6 VS ai5	88.8	2.3	8.9	65.5	13.7	20.8	77.1	8.0	14.9
ai6 VS ai6	30.9	16.9	52.2	17.6	31.3	51.1	24.3	24.1	51.6

上記の結果 から、以下のような 考察 を行いました。

• ai6 は、これまでに作成 した すべての AI に対して 大きく勝ち越す ので、ルール 6 の 効果 が 非常に大きい ことが 確認 できる
• ai4 に対して、勝率が高い ので、ai4 には 欠陥がありそう であることが 再確認 できる
• ai6 の 通算の勝率 は、相手 が ai5 のほうが ai3 より高い ので、ai6 を基準 とした 強さ は、ai3 > ai5 のように見えるかもしれないが、敗率 は ai5 のほうが ai3 よりかなり大きい ので、ai6 を基準 とした 強さ は、ai3 < ai5 であると 考察 できる
• 自分自身 との 対戦 では、約 50 % で 引き分け になるので、〇× ゲーム は、強い AI どうし が 対戦 すると、引き分け の 可能性 が 高くなる ゲームであることが 推測 できる

ルールその 7（ルール3 と ルール 6 の併用）

ルール 3 と ルール 6 は、完全に 異なるアプローチ のルールなので、両方 のルールを 併用 することが できます。そこで、両方のルールを併用した下記の ルール 7 を考えます。

1. 真ん中 の マス が 空いていれば、そこに着手 する（ルール 3）
2. 勝てるマス が 存在 すれば、そこに着手 する（ルール 6）
3. そうでなければ、合法手 を 着手 した 局面 のうち、次 の 相手の手番 で、相手が着手 すると 相手が勝利 するマスが 存在すれば 、そこに着手 して 邪魔 をする（ルール 6）
4. 上記のいずれでもなければ ランダム なマスに 着手 する

この ルール 7 で着手を行う ai7 は、下記のように 簡単に記述 することができます。

• 2、3 行目：(1, 1) のマスが 空いている 場合に、(1, 1) を 返り値 として 返す（ルール 3）
• 4 行目：ルール 6 で 着手 を 選択 する、ai6(mb) を 呼び出し 、その 返り値 を 返す

def ai7(mb):
    if mb.board[1][1] == Marubatsu.EMPTY:
        return 1, 1
    return ai6(mb):

ai2 との対戦

下記のプログラムで、基準となる ai2 との対戦を行います。

ai_match(ai=[ai7, ai2])

実行結果（実行結果はランダムなので下記とは異なる場合があります）

ai7 VS ai2
count     win    lose    draw
o        9578      22     400
x        8227     240    1533
total   17805     262    1933

ratio     win    lose    draw
o       95.8%    0.2%    4.0%
x       82.3%    2.4%   15.3%
total   89.0%    1.3%    9.7%

下記は、上記の結果を表に加えたものです。

関数名	o 勝	o 負	o 分	x 勝	x 負	x 分	勝	負	分	欠陥
ai1	78.1	17.5	4.4	44.7	51.6	3.8	61.4	34.5	4.1	あり
ai2	58.7	28.8	12.6	29.1	58.6	12.3	43.9	43.7	12.5
ai3	69.3	19.2	11.5	38.9	47.6	13.5	54.1	33.4	12.5
ai4	83.0	9.5	7.4	57.2	33.0	9.7	70.1	21.3	8.6	あり
ai5	81.2	12.3	6.5	51.8	39.8	8.4	66.5	26.0	7.4
ai6	88.9	2.2	8.9	70.3	6.2	23.5	79.6	4.2	16.2
ai7	95.8	0.2	4.0	82.3	2.4	15.3	89.0	1.3	9.7

表から、ai7 の成績は、ai6 よりも 大幅に向上 することがわかります。従って、ルール 3 と ルール 6 を 併用 することが 有効である ことがわかりました。

他の AI との対戦

ai3、ai4、ai5、ai6 と 自分自身 と 対戦 してみます。

ai_match(ai=[ai7, ai3])

実行結果（実行結果はランダムなので下記とは異なる場合があります）

ai7 VS ai3
count     win    lose    draw
o        9580      19     401
x        6130     582    3288
total   15710     601    3689

ratio     win    lose    draw
o       95.8%    0.2%    4.0%
x       61.3%    5.8%   32.9%
total   78.5%    3.0%   18.4%

ai_match(ai=[ai7, ai4])

実行結果（実行結果はランダムなので下記とは異なる場合があります）

ai7 VS ai4
count     win    lose    draw
o       10000       0       0
x        6581    2934     485
total   16581    2934     485

ratio     win    lose    draw
o      100.0%    0.0%    0.0%
x       65.8%   29.3%    4.9%
total   82.9%   14.7%    2.4%

ai_match(ai=[ai7, ai5])

実行結果（実行結果はランダムなので下記とは異なる場合があります）

ai7 VS ai5
count     win    lose    draw
o        9540      36     424
x        8109     543    1348
total   17649     579    1772

ratio     win    lose    draw
o       95.4%    0.4%    4.2%
x       81.1%    5.4%   13.5%
total   88.2%    2.9%    8.9%

ai_match(ai=[ai7, ai6])

実行結果（実行結果はランダムなので下記とは異なる場合があります）

ai7 VS ai6
count     win    lose    draw
o        3024     431    6545
x         706    1556    7738
total    3730    1987   14283

ratio     win    lose    draw
o       30.2%    4.3%   65.5%
x        7.1%   15.6%   77.4%
total   18.6%    9.9%   71.4%

ai_match(ai=[ai7, ai7])

実行結果（実行結果はランダムなので下記とは異なる場合があります）

ai7 VS ai7
count     win    lose    draw
o        2989     414    6597
x         397    3039    6564
total    3386    3453   13161

ratio     win    lose    draw
o       29.9%    4.1%   66.0%
x        4.0%   30.4%   65.6%
total   16.9%   17.3%   65.8%

下記は、上記の結果を表にまとめたものです。

関数名	o 勝	o 負	o 分	x 勝	x 負	x 分	勝	負	分
ai7 VS ai2	95.8	0.2	4.0	82.3	2.4	15.3	89.0	1.3	9.7
ai7 VS ai3	95.8	0.2	4.0	61.3	5.8	32.9	78.5	3.0	18.4
ai7 VS ai4	100.0	0.0	0.0	65.8	29.3	4.9	82.9	14.7	2.4
ai7 VS ai5	95.4	0.4	4.2	81.1	5.4	13.5	88.2	2.9	8.9
ai7 VS ai6	30.2	4.3	65.5	7.1	15.6	77.4	18.6	9.9	71.4
ai7 VS ai7	29.9	4.1	66.0	4.0	30.4	65.6	16.9	17.3	65.8

上記の結果 から、以下のような 考察 を行いました。

• ai7 は、ai5 以前 の AI に 対して は 圧倒的な強さ を持つため、ルール 6 は 強い AI を 作成 する際に 非常に重要 である 可能性 が 高い
• ai7 は、ai6 に対して 通算 の 勝率 が 敗率より高い ので、真ん中 のマスに 優先的に着手 することが 有効 であることが 確認 できる
• ai7 が 〇を担当 した場合で、ai6 と ai7 に対する 成績 が ほぼ同じ になるが、その理由は以前の記事で説明した理由と同じである
• ai7 VS ai6 や ai7 VS ai7 は、引き分け率 が 約 50% の ai6 VS ai6 より もさらに 引き分け率 が 高い ので、やはり、〇× ゲーム は、強い AI どうし が 対戦 すると、引き分け の 可能性 が 高くなる ゲームであるという 推測 が 正しい可能性 が 高く なった
• ai7 が 〇 を担当 した場合は ai4 に対する 勝率 が 100% になるので、ai4 は、× を担当 する場合に 致命的な欠陥 があることが 再確認 できた

ルール 3 と ルール 6 の順番

先程の ルール 7 では、ルール 3 を 適用した後 で ルール 6 を 適用 していますが、下記のように、その 順番を逆 にしたルールも考えられます。

1. 勝てるマス が 存在 すれば、そこに着手 する（ルール 6）
2. そうでなければ、合法手 を 着手 した 局面 のうち、次 の 相手の手番 で、相手が着手 すると 相手が勝利 するマスが 存在すれば 、そこに着手 して 邪魔 をする（ルール 6）
3. 真ん中 の マス が 空いていれば、そこに着手 する（ルール 3）
4. 上記のいずれでもなければ ランダム なマスに 着手 する

今回の記事の最初で、ルールの 手順 の 順番 を 変える と、結果 が 変化する場合がある ので 注意 する 必要 があると説明しましたが、ルール 7 の場合は、ルール 3 と ルール 6 を適用する 順番 を 変えても、結果 は 変化しません。その理由について考えてみて下さい。

ルール 3 によって着手が行われる条件

ルール 3 によって 着手 が行われる 条件 は、真ん中のマス が 空いている ことです。従って、真ん中 のマスが 空いていない場合 は、ルール 3 によって 着手 は 行われません。

ルール 6 によって着手が行われる条件

ルール 6 によって 着手 が行われる 条件 は、次 の 自分の着手 で 自分が勝利できる か、次 の 相手の着手 で 相手が勝利できる 場合です。

〇× ゲーム では、自分のマーク を 3 つ並べる ことで 勝利する ので、〇 も × も、1、2 回目 の着手で 勝利 することは あり得ません。従って、〇 と × の 1 回目 の着手で、ルール 6 が 適用 されることは ありません。

〇 の 1 回目の着手の場合

上記から、〇 の 1 回目 の着手で、ルール 6 が 適用 されることは ありません。従って、ルール 3 と ルール 6 を適用する 順番 は、〇 の 1 回目 の着手に 影響 を 与えません。

〇 の 1 回目 の着手では、真ん中 のマスは 必ず空いている ので、ルール 3 が 適用 されて 真ん中 のマスに 着手 が行われます。

× の 1 回目の着手の場合

同様の理由 で、× の 1 回目 の着手で、ルール 6 が 適用 されることは ありません。従って、ルール 3 と ルール 6 を適用する 順番 は、× の 1 回目 の着手に 影響 を 与えません。

真ん中 のマスが 空いている 場合は ルール 3 が 適用 されて 真ん中 のマスに 着手 が行われ、空いていない場合はランダムなマスに着手が行われます。その結果 として、× の 1 回目 の 着手の後 では、必ず真ん中 のマスが 空ではなくなります。

2 回目以降の着手の場合

上記の事から、2 回目以降 の 着手 では、〇 の場合 も、× の場合 も 真ん中 のマスが 空いていない ので、ルール 3 が 適用 されることは ありません。従って、ルール 3 と ルール 6 を適用する 順番 は、2 回目以降 の着手に 影響 を 与えません。

以上から、すべての場合 で、ルール 3 と ルール 6 を適用する 順番 は、ルール 7 の着手に 影響 を 与えない ことがわかります。

今回の記事のまとめ

今回は、以下の表のようなアルゴリズムの ai6 を実装しました。また、これまでに作成 した ルール 3 と ルール 6 を 組み合わせ た ai7 を実装し、その 2 つのルール を 組み合わせる ことで かなり強い AI を 作成 することができたことを確認しました。

まだ 最強ではありません が、ai7 は それなりに強い AI になっていると思いますので、実際 に mb.play(ai=[None, ai7]) と mb.play(ai=[ai7, None]) を実行して ai7 と対戦 して、その 強さを確認 してみて下さい。

関数名	アルゴリズム
ai6	勝てる場合に勝つ そうでない場合は相手の勝利を阻止する そうでない場合は ランダム なマスに 着手 する
ai7	真ん中のマスが空いていればそこに着手する そうでない場合は、勝てる場合に勝つ そうでない場合は相手の勝利を阻止する そうでない場合は ランダム なマスに 着手 する

本記事で入力したプログラム

以下のリンクから、本記事で入力して実行した JupyterLab のファイルを見ることができます。

今回の記事では、marubatsu.py は修正していないので、marubatsu_new.py はありません。

以下のリンクは、今回の記事で更新した ai.py です。

次回の記事

1. 正確には、強さが変わらない場合もあります ↩

2. 最大 としたのは、× が勝利 する合法手が 見つかった時点 で手順 3 の 処理が終了 するからです ↩

3. 合法手 が 1 つ の場合は 1 * 0 = 0 になると思う人がいるかもしれませんが、今回の記事の最初の方で説明したように、合法手 が 1 つ しかない場合は、ルール 6 は 適用しません ↩