目次と前回の記事

これまでに作成したモジュール

以下のリンクから、これまでに作成したモジュールを見ることができます。

これまでに作成した AI

これまでに作成した AI のアルゴリズムは以下の通りです。

ルール	アルゴリズム
ルール1	左上から順に空いているマスを探し、最初に見つかったマスに着手する
ルール2	ランダムなマスに着手する
ルール3	真ん中のマスに優先的に着手する既に埋まっていた場合はランダムなマスに着手する
ルール4	真ん中、隅のマスの順で優先的に着手する既に埋まっていた場合はランダムなマスに着手する
ルール5	勝てる場合に勝つそうでない場合はランダムなマスに着手する
ルール6	勝てる場合に勝つそうでない場合は相手の勝利を阻止するそうでない場合はランダムなマスに着手する
ルール6改	勝てる場合に勝つそうでない場合は相手が勝利できる着手を行わないそうでない場合はランダムなマスに着手する
ルール7	真ん中のマスに優先的に着手するそうでない場合は勝てる場合に勝つそうでない場合は相手の勝利を阻止するそうでない場合はランダムなマスに着手する
ルール7改	真ん中のマスに優先的に着手するそうでない場合は勝てる場合に勝つそうでない場合は相手が勝利できる着手を行わないそうでない場合はランダムなマスに着手する
ルール8	真ん中のマスに優先的に着手するそうでない場合は勝てる場合に勝つそうでない場合は相手が勝利できる着手を行わないそうでない場合は、次の自分の手番で勝利できるように、「自 2 敵 0 空 1」が 1 つ以上存在する局面になる着手を行うそうでない場合はランダムなマスに着手する

基準となる ai2 との 対戦結果（単位は %）は以下の通りです。太字は ai2 VS ai2 よりも 成績が良い 数値を表します。欠陥の列は、アルゴリズム に欠陥があるため、ai2 との 対戦成績 が 良くても強い とは 限らない ことを表します。欠陥の詳細については、関数名のリンク先の説明を見て下さい。

関数名	o 勝	o 負	o 分	x 勝	x 負	x 分	勝	負	分	欠陥
`ai1` `ai1s`	78.1	17.5	4.4	44.7	51.6	3.8	61.4	34.5	4.1	あり
`ai2` `ai2s`	58.7	28.8	12.6	29.1	58.6	12.3	43.9	43.7	12.5
`ai3` `ai3s`	69.3	19.2	11.5	38.9	47.6	13.5	54.1	33.4	12.5
`ai4` `ai4s`	83.0	9.5	7.4	57.2	33.0	9.7	70.1	21.3	8.6	あり
`ai5` `ai5s`	81.2	12.3	6.5	51.8	39.8	8.4	66.5	26.0	7.4
`ai6`	88.9	2.2	8.9	70.3	6.2	23.5	79.6	4.2	16.2
`ai6s`	88.6	1.9	9.5	69.4	9.1	21.5	79.0	5.5	15.5
`ai7` `ai7s`	95.8	0.2	4.0	82.3	2.4	15.3	89.0	1.3	9.7
`ai8s`	98.2	0.1	1.6	89.4	2.5	8.1	93.8	1.3	4.9

`enum_markpats` の問題点

前回の記事で定義した enum_markpats は、マークのパターンを列挙 したデータを list で表現 しましたが、list の要素 には、同じデータ が 複数存在できる ので、例えば下記のプログラムのように、ゲーム開始時 の局面に対して、enum_markpats を呼び出して表示すると、同じマークのパターンが 8 回も表示 されてしまいます。

from marubatsu import Marubatsu
from pprint import pprint

mb = Marubatsu()
pprint(mb.enum_markpats())

実行結果

[defaultdict(<class 'int'>, {'.': 3}),
 defaultdict(<class 'int'>, {'.': 3}),
 defaultdict(<class 'int'>, {'.': 3}),
 defaultdict(<class 'int'>, {'.': 3}),
 defaultdict(<class 'int'>, {'.': 3}),
 defaultdict(<class 'int'>, {'.': 3}),
 defaultdict(<class 'int'>, {'.': 3}),
 defaultdict(<class 'int'>, {'.': 3})]

プログラムが正しく動作する かどうかという観点では、list でも 全く問題 はないのですが、enum_markpats で 知りたい のは、特定の マークのパターン が 存在するか どうかなので、同じマークのパターンを表す データ が、上記のように 8 つも存在 するのは無駄と言えるでしょう。この問題は、set という データ型 を利用することで解決できます。

英単語 としての set は集合を表し、Python の set は 文字通り、集合を扱うための データ型 です。set は list のように 頻繁に使われる わけでは ありません が、適切な場面 で利用することで、集合の性質 を持つ データを扱う プログラムが 記述しやすく なったり、処理の 効率を上げる ことができるので、今回の記事では、使い方を説明することにします。

集合とは何か

set の説明を行う前に、数学の用語 としての集合の説明を行います。

数学用語 の集合とは、ものの集まり を表す用語で、集合の中に 含まれるもの のことを、元（げん）または要素（element）と呼びます。本記事 では要素と表記します。

集合は、現代数学 における 最も基本 となる概念の一つです。このように説明すると、難しそうだ と思う方が多いかもしれませんが、本記事では、それほど 難しい 集合の性質は 扱わない ので心配する必要はありません。

参考までに、wikipedia の集合の項目のリンクを下記に示します。

有限集合と無限集合

集合には、整数の集合 のように、無限個 の 要素を持つ ものがあります。無限個 の要素を持つ集合を 無限集合、数に限りがある 有限個 の要素を持つ集合を 有限集合 と呼びます。Python の set は 無限集合 を扱うことは できない と思います¹ので、本記事では、有限集合のみ を扱い、以降は集合と記述した場合は、有限集合 のことを表すことにします。

集合の性質

集合は、主に下記のような性質を持ちます。なお、厳密な 集合の性質 について知りたい方は、数学を 学ぶ必要 があります。

集合の中 に 同じ要素 は重複して 存在しない
集合の中 の要素に順番は 存在しない
要素が 存在しない 場合も、集合と みなされる。そのような集合を、空集合 と呼ぶ
あるもの が集合の要素に 含まれるか どうかを表す、帰属関係 を 考える ことができる
ある集合 の すべての要素 が、別の集合 の要素に 含まれるか どうかを表す、包含関係 を 考える ことができる
集合どうし に対する、さまざまな演算 を行うことができる。例えば、集合 A と 集合 B に対して、集合和 という演算を行うことで、A と B の 要素を持つ 集合が作成される

enum_markpats が計算する、マークのパターン を列挙した データ は、以下のように、集合の性質 を 満たす ので、そのデータを 集合とみなす ことができます。

同じ マークのパターン が 重複する必要がない
順番は 関係がない
特定の マークのパターン が 含まれるか という、帰属関係 を考えることができる

ピンとこない人がいるのではないかと思いますので、上記の 集合の性質 について、wikipedia のリンク先で紹介されている トランプ を 具体例 として説明します。

集合の例

上記のリンク先で例として挙げられている トランプ を使った 集合の例 を紹介します。集合は、一般的に { } の中 に要素を , で 区切って表記 するので、そのように表記します。

トランプ の マークの集合 は { ♥, ♠, ♦, ♣ } の 4 つ の要素を持つ集合です。

トランプ の 数字の集合 は { A, 2, 3, 4, 5, 6, 7, 8, 9, 10, J, Q, K } の 13 個 の要素を持つ集合です。なお、この集合の中には A、J、Q、K という文字が 含まれて いますが、多くの場合 では、それらは 1、11、12、13 という数字と みなされる ので、本記事では トランプ の 数字の集合 を { 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13 } とします。

同じ要素が重複しない

トランプ では、それぞれのマーク を持つカードは 13 枚ずつ ありますが、トランプ の マーク の集合では、トランプの カード から マークだけ を 取り出した、{ ♥, ♥, ♥, (♥ が 13 個並ぶ), ♠, ♠, ・・・以下略 } という、マークを並べたもの を集合と 考える ことは ありません。その理由は、集合が、その中 に 特定のものが存在するか どうかを表すことが目的で 作られて おり、ものが 何個存在する かという情報は不要だからです。従って、重複するものは 1 つ に まとめられ、トランプ の マーク の集合は、{ ♥, ♠, ♦, ♣ } となります。

集合の要素に順番はない

集合の 要素の中 に 特定の要素 が存在するかどうかを表す際に、要素の順番の情報は必要では ありません。例えば、トランプ の マーク を表す集合は、♥、♠、♦、♣ の 4 つの要素 を持つという 性質のみ が 求められる ので、マークの順番 に 意味はありません。

集合を表記する際には、何らかの順番 で要素を 記述する必要 がありますが、その順番に 意味はありません。そのため、{ ♥, ♠, ♦, ♣ } と { ♦, ♣, ♥, ♠ } のように、表記の順番 が 異なっていても、この 2 つは 同じ集合 と みなされます。

トランプ の数字の集合のように、集合に含まれる 要素そのもの に 大きさなど の 順番が存在する 場合は、一般的 に { 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13 } のように、分かりやすさ を重視して順番に並べて表記しますが、この場合でも、集合の要素の順番に 意味はありません。従って、トランプ の数字の集合は、{ 2, 6, 13, 1, 11, 10, 12, 8, 9, 7, 4, 3, 5 } のように、任意の順番 で要素を表記しても かまいません。

複数のもの を 扱う際 に、ものの 順番が重要 な場合は、集合を利用することは できない 点に注意して下さい。Python の場合は、set ではなく、list を利用 する必要があります。

例えば、トランプ の マーク や数字の種類を扱いたい場合は、集合を利用することが できます が、トランプ の カード を シャッフルした後 に 並べられた 52 枚のカードの 数字の内容 を上から順番に 扱いたい 場合は、「重複した数字 を 扱う必要 がある」、「順番が必要である」という理由から、集合として扱うことは できません。

空集合の例

例えば、トランプ で「20 以上 の数字」の集合は、そのようなトランプのカードが 存在しない ので 空集合 になります。なお、数学では 空集合 には { } や ∅ などの 複数の表記 がありますが、Python で {} を記述すると、空の dict を表す点に 注意が必要 です。

帰属関係

帰属関係 とは、あるもの が、集合に 含まれている ことを表す関係です。

帰属関係 が あるか どうかを 調べる ことは、無限集合 の場合はそれほど 簡単な話ではありません が、有限集合 の場合は、すべて の 集合の要素 を 調べる ことで、要素の数が多い場合は時間がかかるかもしれませんが、必ず判定 することが できます。

例えば、トランプ の マーク の集合に、♠ が 含まれ、■（四角の記号）が 含まれない ことは、4 つ の要素を 調べる ことで 簡単に判定 できます。

包含関係と相当関係

包含関係 は、〇×ゲーム の AI を作成 する際に 利用しない ので、難しいと思った方 は簡単に 目を通しておくだけで良い と思います。後で 必要になった時 に 読み返して 下さい。

包含関係 とは、ある集合 の すべての要素 が、別の集合 の要素に 含まれる（帰属関係 がある）という関係を表します。例えば、トランプ の 赤いマーク の集合である { ♥, ♦ } の すべて の要素は、トランプ の マーク の集合の { ♥, ♠, ♦, ♣ } の要素に 含まれる ので、包含関係 があります。包含関係 には方向があり、集合 A の すべての要素 が 集合 B に 含まれる ことを、「A は B に包含される」または「B は A を包含する」のように表記します。

集合 A が 集合 B に 包含されるか どうかの判定は、A の それぞれの要素 が、B に 帰属するか どうかを判定し、すべて の A の要素 が B に帰属 する場合に「A は B に包含される」と判定することが できます。従って、有限集合 の場合は、2 つ の集合の間に 包含関係 が あるか どうかを、必ず判定 することが できます。

包含関係 は 難しそう思える かもしれませんが、図で示すとわかりやすいでしょう。包含関係 は、下図の 黄色の集合 が、緑の集合の中 に 完全に含まれる という関係です。

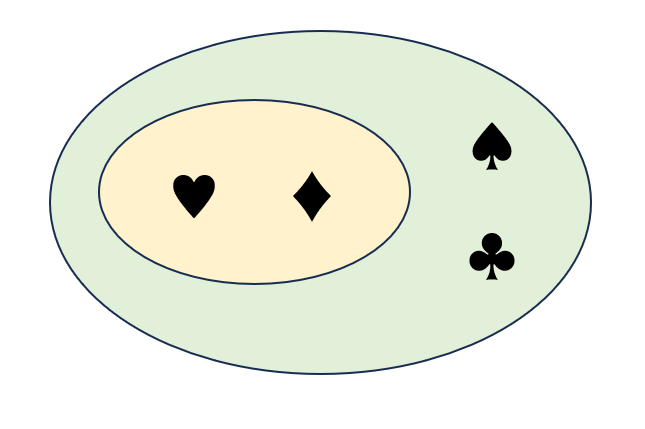
2 つの集合 の要素が 完全に等しい ことを「2 つの集合が 相当関係 である」、または「2 つの集合が 等しい」と呼びます。A が B に包含される ことを、数学では「$A ⊂ B$」と表記します。また、A と B が 相当である（等しい）ことを「$A = B$」、A と B が 相当でない（等しいくない）ことを「$A ≠ B$」と表記します。

A と B が相当であるか（$A = B$）の判定は、包含関係 によって、「$A ⊂ B$ かつ $B ⊂ A$ である」場合に相当であると判定できます。証明は長くなるので省略しますが、それほど難しくはないので、興味がある方は調べてみて下さい。従って、有限集合 であれば、必ず相当関係があるか どうかを判定することが できます。

「A が B に包含される」（$A ⊂ B$）場合のことを「A は B の 部分集合」であると表記します。また、「A が B に包含される」が「A と B は相当でない」場合（$A ⊂ B$ かつ $A ≠ B$）のことを「A は B の 真部分集合」と表記します。

「A が B に包含される」（$A ⊂ B$）が 満たされない 場合に、「B が A に包含される」（$A ⊃ B$）が 満たされるとは限らない 点に注意して下さい。例えば、トランプ の偶数の集合 { 2, 4, 6, 8, 10, 12 } を A、3 の倍数 の集合 { 3, 6, 9, Q } を B とした場合に、集合 A は下図の黄色の楕円、集合 B は緑色の楕円で 表されます。図からわかるように、A は B に 包含されません が、B も A に 包含されません。

集合どうしの演算の例

集合どうし の演算も、〇×ゲームの AI では 利用しない ので、ここでは 集合和 という演算 のみを紹介 します。他の演算については、この後で紹介します。

トランプ で、偶数の数字 の集合 { 2, 4, 6, 8, 10, 12 } と 3 の倍数の数字 の集合 { 3, 6, 9, Q } の 集合和 は、それらの両方の要素を持つ { 2, 3, 4, 6, 8, 9, 10, 12 } になります。

集合和 は、下図の 黄色の集合 と、緑の集合 の 両方の要素 を含む集合になります。

set の使い方

Python の set は、上記のような 有限集合 の性質を持つデータを表現する データ型 です。

上記で説明した 集合の性質 と対応しながら、set の使い方 の説明を行います。

set の詳細については、下記のリンク先を参照して下さい。

set の作成

set は以下の いずれかの方法 で作成することができます。

set のリテラル

set の リテラル は list と 似ています が、外側を 囲う記号 が [ と ] ではなく、{ と } である点が 異なります。なお、{ と } で 囲んで記述 する点は dict のリテラルと同じですが、キー:キーの値 ではなく、set の要素 となるデータ だけを記述 する点が 異なります。

下記は、トランプ の マーク を要素とする set を print で表示 するプログラムです。print で表示 した場合は、set のリテラル と 同じ内容 が表示されます。

print({"♠", "♥", "♦", "♣"})

実行結果

{'♠', '♥', '♦', '♣'}

set は、集合と同様に、同じ要素 が 重複しない という 性質を持つ ので、下記のプログラムのように、set の リテラル に、同じデータ を 複数記述 した場合は、同じデータ が 1 つにまとめられた set が作成されます。

print({"♠", "♠", "♠", "♥", "♥", "♥", "♦", "♦", "♦", "♣", "♣", "♣"})

実行結果

{'♠', '♥', '♦', '♣'}

空の set のリテラル

空集合 を表す、要素が 存在しない set のことを、空の set と呼びます。空の set の リテラルだけ は、{} ではなく、set() のように記述する 必要がある 点に注意して下さい。その理由は、{} のように記述すると、空の dict と みなされる からです。空の set を print で表示 すると、下記のプログラムの 1 行目 のように set() が表示 されます。

print(set())  # 空の set のみ、必ずこのように記述する必要がある
print({})     # こちらは空の dict を表す

実行結果

set()
{}

list からの作成

上記で利用した、set は、データ型 を表す 組み込み型のクラス です。下記のプログラムのように、set の引数に list を記述 することで、記述した list と同じ要素 を持つ set の インスタンス を作成することができます。2 行目 のように、同じ要素 を 複数持つ list を記述した場合は、先程と同様 に、同じデータ が 1 つ に まとめられた set が作成されます。

print(set(["♠", "♥", "♦", "♣"]))
print(set(["♠", "♠", "♠", "♥", "♥", "♥", "♦", "♦", "♦", "♣", "♣", "♣"]))

実行結果

{'♦', '♥', '♣', '♠'}
{'♦', '♥', '♣', '♠'}

なお、下記のプログラムのように、組み込み型のクラスである list の 実引数 に set を記述 することで、set を list に変換 することも できます。そのことは、実行結果 の 外側の記号 が、list を表す [ と ] であることから確認できます。

print(list({"♠", "♥", "♦", "♣"}))

実行結果

['♠', '♥', '♦', '♣']

set 内包表記

list 内包表記 と同様の set 内包表記 で、下記のプログラムのように set を作成 することが できます。list 内包表記 との違いは、外側の記号 が { と } である点だけです。

print({ i for i in range(10) })

実行結果

{0, 1, 2, 3, 4, 5, 6, 7, 8, 9}

set が扱えるデータ

list は、任意の オブジェクト を要素にできましたが、set は以前の記事で説明した ハッシュ可能 なオブジェクトのみを要素に できます。

list のような、ハッシュ可能 でない オブジェクトを set の要素 にしようとすると、下記のプログラムのように エラーが発生 します。なお、set がハッシュ可能なオブジェクトしか扱えない理由については後で説明します。

print({1, []})

実行結果

---------------------------------------------------------------------------
TypeError                                 Traceback (most recent call last)
Cell In[8], line 1
----> 1 print({1, []})

TypeError: unhashable type: 'list'

上記のエラーメッセージは、以下のような意味を持ちます。

TypeError
データ型（type）に関するエラー
unhashable type: 'list'
list はハッシュ可能（hashable）なデータ型（type）ではない（un）

帰属関係の判定

あるデータ が、set の要素に 含まれるか どうかという 帰属判定 は、下記のプログラムのように、list と同様 の方法で、in 演算子 を使って 判定できます。

marks = {"♠", "♥", "♦", "♣"}
print("♠" in marks)  # ♠ は marks に含まれる
print("■" in marks)  # ■（四角）は marks に含まれない

実行結果

True
False

set に 含まれない かどうかの判定も、list と同様 に not in 演算子 を利用できます。

marks = {"♠", "♥", "♦", "♣"}
print("♠" not in marks)
print("■" not in marks)

実行結果

False
True

包含関係と相当関係（等しい）の判定

下記の表の 比較演算子 によって、set どうし の 包含関係 や 相当関係 を判定することができます。下記の「True になる条件」の列は、演算子の左右 に A と B という 2 つ の set を記述して比較した場合の説明です。また、参考までに 数学の用語 を表に示します。

演算子	`True` になる条件	数学の記法と用語
`==`	A と B が等しい（同じ要素を持つ）	$A = B$ A と B は相当（等しい）
`!=`	A と B が等しくない（異なる要素がある）	$A ≠ B$
`>`	B のすべての要素を A が含むただし、A と B が等しい場合を除く	$A ⊃ B$ かつ $A ≠ B$ B は A の真部分集合
`>=`	B のすべての要素を A が含む A と B が等しくても良い	$A ⊃ B$ B は A の部分集合
`<`	A のすべての要素を B が含むただし、A と B が等しい場合を除く	$A ⊂ B$ かつ $A ≠ B$ A は B の真部分集合
`<=`	A のすべての要素を B が含む A と B が等しくても良い	$A ⊂ B$ A は B の部分集合

set には、上記の演算子 と 同じ処理 を行う メソッド が用意されています。また、上記では 行えない 、A と B が 共通の要素を持たない ことを判定する isdisjoint というメソッドがあります。興味がある方は、このリンク先を参照して下さい。

比較演算子の利用例

下記のプログラムは、上記の演算子 の 利用例 です。A と B は、set の リテラル を記述する際に、異なる順番 で 4 つのマーク を記述していますが、先ほど説明したように、集合の要素 に 順番はない ので、A と B は同一の set と みなされます。その他 については、一つ一つを説明すると長くなりすぎるので説明は省略します。上記の表 と、下記のプログラムの 実行結果 を各自で 見比べて下さい。

A = {"♠", "♥", "♦", "♣"}
B = {"♦", "♥", "♠", "♣"}
C = {"♥", "♦"}            # 赤いマークのみの集合
D = {"♠", "♥", "■"}       # トランプのマークと関係ない ■ が混じっている

print("A == B", A == B)
print("A == C", A == C)
print("A == D", A == D)
print()

print("A != B", A != B)
print("A != C", A != C)
print("A != D", A != D)
print()

print("A > B", A > B)
print("A > C", A > C)
print("A > D", A > D)
print()

print("A >= B", A >= B)
print("A >= C", A >= C)
print("A >= D", A >= D)
print()

print("B < A", B < A)
print("C < A", C < A)
print("D < A", D < A)
print()

print("B <= A", B <= A)
print("C <= A", C <= A)
print("D <= A", D <= A)

実行結果

A == B True
A == C False
A == D False

A != B False
A != C True
A != D True

A > B False
A > C True
A > D False

A >= B True
A >= C True
A >= D False

B < A False
C < A True
D < A False

B <= A True
C <= A True
D <= A False

list に対して == 演算子 で比較した場合は、下記のプログラムのように、要素の順番 も 含めて同じ でなければ True と みなされません。その点に注意 して下さい。

A = ["♠", "♥", "♦", "♣"]
B = ["♦", "♥", "♠", "♣"]

print(A == B)

実行結果

False

set どうしの演算

下記の表の 演算子 によって、set どうし の演算を行い、新しい set を作成することができます。下記の説明では、A と B という 2 つの集合 を 演算子で演算 した場合の説明です。

演算子	関係
`\|`	A と B の両方の要素を持つ、和集合を計算する
`&`	A と B の共通する要素を持つ、積集合を計算する
`-`	A の要素から、B の要素を削除した、差集合を計算する B にのみ存在する要素は差集合には含まれない
`^`	A と B のいずれかのみに含まれる、対象差を計算する

下記のプログラムは、上記の演算子 の 利用例 です。実行結果からわかるように、一部の演算 では、print で表示 される 要素の順番 が変化しますが、先ほど説明したように set の 要素の順番 に 意味はない ので、表示の順番 が 変わっても問題はありません。

A = {2, 4, 6, 8, 10, 12}  # トランプの偶数の数字
B = {3, 6, 9, 12}         # トランプの 3 の倍数の数字

print("A | B", A | B)
print("A & B", A & B)
print("A - B", A - B)
print("A ^ B", A ^ B)

実行結果

A | B {2, 3, 4, 6, 8, 9, 10, 12}
A & B {12, 6}
A - B {8, 2, 10, 4}
A ^ B {2, 3, 4, 8, 9, 10}

上記のうち、和集合 を計算する 演算子 は、数値の 和を計算 する際に利用する + ではない 点に 注意が必要 です。実際に set に対して + 演算子 で計算を行おうとすると、下記のプログラムのように、エラーが発生 します。

print({1, 2} + {3})

実行結果

---------------------------------------------------------------------------
TypeError                                 Traceback (most recent call last)
Cell In[14], line 1
----> 1 print({1, 2} + {3})

TypeError: unsupported operand type(s) for +: 'set' and 'set'

上記のエラーメッセージは、以下のような意味を持ちます。

TypeError
データ型（type）に関するエラー
unsupported operand type(s) for +: 'set' and 'set'
+ 演算子は set と（and）set 型（types）の値（operand²）の演算をサポートしていない（unsupported）

set の 和集合 の計算に + が 使われない理由 の一つは、set に対する 和集合 の計算では、重複する要素 が 1 つ に まとめられる からです。それに対して、list の結合 を行う + 演算子 では、下記のプログラムのように、重複する要素 が まとめられる ことは ありません。

print([1, 2, 3] + [1, 2])

実行結果

[1, 2, 3, 1, 2]

他の理由 としては、和集合の計算 が、まだ説明していない、| 演算子を使う、ビット演算 の 論理和の計算 に 似ている という理由があると思います。

set に対するさまざまな操作

set に対して行うことができる、さまざまな操作 について説明します。

`add` メソッドによる要素の追加

set に対して 要素を追加 する場合は、下記のプログラムのように、add メソッド を利用します。list に要素を追加する append メソッド とは 名前が異なる 点に注意して下さい。

a = { 1, 2 }
a.add(3)          # append ではない点に注意
print(a)

実行結果

{1, 2, 3}

また、以前の記事のノートで紹介した、list の 要素の追加 を行う際に利用できた += 演算子 は、set に対して行うと、下記のプログラムのように エラーが発生 する点にも 注意が必要 です。同様の処理 は、次に説明する |= 演算子 で行うことができます。

a += {4, 5}

実行結果

---------------------------------------------------------------------------
TypeError                                 Traceback (most recent call last)
Cell In[32], line 1
----> 1 a += {4, 5}

TypeError: unsupported operand type(s) for +=: 'set' and 'set'

上記のエラーメッセージは、以下のような意味を持ちます。

TypeError
データ型（type）に関するエラー
unsupported operand type(s) for +: 'set' and 'set'
+= 演算子は set と（and）set 型（types）の値（operand²）の演算をサポートしていない（unsupported）

`|=` 演算子による要素の追加

|= 演算子を使って、set に 別の set の要素を すべて追加 することができます。下記のプログラムの 3 のように、重複する要素 がある場合は、一つに まとめられます。

a = {1, 2, 3}
a |= {3, 4, 5}
print(a)

実行結果

{1, 2, 3, 4, 5}

`|=` 演算子に関する注意点

|= 演算子は、見た目上 は、前後の set に対して | 演算子 によって 和集合 を計算し、|= の前 に 記述された変数 に代入するという処理を行うように 見えるかもしれません。

例えば、下記のプログラムの 1 行目 と、2 行目 は 同じ処理 を行うように 見えるかもしれません が、実際には 異なる処理 を行う点に 注意が必要 です。

a |= {3, 4, 5}
a = a | {3, 4, 5}

上記の 1 行目 では、a に代入された set に += の 右の set の 要素が追加 されます。一方 2 行目 では、a | {3, 4, 5} の 計算結果 を表す 新しい set が作成され、その 新しい set で a が参照する オブジェクトを更新 する点が異なります。

|= 演算子では、|= の 前に記述 された変数が参照するオブジェクトは 変化しない
= 演算子では、= の 前に記述 された変数が参照するオブジェクトは 変化する

そのことは、下記のプログラムのように、変数が参照する オブジェクトの id を表示することで確認できます。この違い を 理解していない と バグが発生 する 可能性 があります。具体例については、そのような状況が実際に起きる場合に紹介する予定です。

a = {1, 2, 3}
print(id(a))     
a |= {3, 4, 5}     # こちらは、a に要素を追加する処理
print(id(a))       # 2 行前と同じ id が表示される

a = {1, 2, 3}
print(id(a))
a = a | {3, 4, 5}  # こちらは、新しい set を作成し、a に代入する処理
print(id(a))       # 2 行前と異なる id が表示される

実行結果

1661492119360
1661492119360
1661492117568
1661492120704

なお、この性質 は、list に対する += 演算子 や、次で説明する 演算子 にも共通します。

set の内容を更新する他の演算子

先程紹介した、&、-、^ に対応する &=、-=、^= 演算子があります。いずれも、演算子の前 に記述された変数に代入されたの set の内容 を、対応する演算子 による 演算の結果 で更新する処理を行い、|= と同様 に、変数が参照する オブジェクト は 変化しません。

下記のプログラムは、それらの演算子の 使用例 です。これらの 演算子 による 演算によって、a の値 が 更新される ので、次の演算 を 行う前 に a に 元の値 を 代入しなおし ています。なお、b の値は 変化しない ので 代入し直す必要 は ありません。

a = {2, 4, 6, 8, 10, 12}
b = {3, 6, 9, 12}

a &= b
print(a)

a = {2, 4, 6, 8, 10, 12}
a -= b
print(a)

a = {2, 4, 6, 8, 10, 12}
a ^= b
print(a)

実行結果

{12, 6}
{2, 4, 8, 10}
{2, 3, 4, 8, 9, 10}

要素の削除

下記の表は、set の 要素を削除 する方法です。pop 以外 の メソッド は 値を返しません。

方法	意味
`remove` メソッド	実引数に記述したものと同じ要素を削除する記述した要素が存在しない場合は、エラーが発生する
`discard` メソッド	実引数に記述したものと同じ要素を削除する記述した要素が存在しない場合は、何も行わない
`pop` メソッド	いずれか 1 つの要素を削除し、削除した値を返すなお、削除する要素は指定できない
`clear` メソッド	すべての要素を削除し、空の set にする
`-=` 演算子	演算子の右に記述した set の要素をすべて削除する

下記のプログラムは、それぞれの 利用例 です。-= 演算子 は 先程説明した ので省略します。なお、pop メソッド は、個人的にはあまり 使い道がない のではないかと思います。

a = {1, 2, 3, 4, 5}

a.remove(5)   # 5 を削除する
print(a)

a.discard(4)  # 4 を削除する
print(a)

a.discard(6)  # 存在しない 6 を discard で指定した場合は何も起こらない
print(a)

print(a.pop()) # いずれか 1 つの要素を削除し、その値を返す
print(a)       # 上の行で表示された値の要素が削除されている

a.clear()      # すべての要素を削除する
print(a)       # 空の set を表す set() が表示される

実行結果

{1, 2, 3, 4}
{1, 2, 3}
{1, 2, 3}
1
{2, 3}
set()

下記のプログラムは、remove メソッド で、存在しない要素 を削除しようとする例で、実行結果からわかるように、エラーが発生 します。

a = {1, 2, 3}
a.remove(5)

実行結果

---------------------------------------------------------------------------
KeyError                                  Traceback (most recent call last)
Cell In[19], line 2
      1 a = {1, 2, 3}
----> 2 a.remove(5)

KeyError: 5

上記のエラーメッセージは、以下のような意味を持ちます。

KeyError
キー（key）に関するエラー
5
5 というキーは存在しない

要素の数の計算

set の 要素の数 は、list と同様 に、組み込み関数 len を使って下記のプログラムのように 計算できます。

print(len({1, 2, 3}))
print(len(set()))      # 空の set の場合の要素の数は 0

実行結果

3
0

for 文による要素の列挙

set は 反復可能オブジェクト なので、for 文 の 反復可能オブジェクト に記述することで、下記のプログラムのように、list と同様 に要素を 順番に取り出す ことができます。

なお、set の要素は、set に 挿入した順番 で 取り出され ますが、&= 演算子などによって set の 要素を更新 した場合などで、順番が変更される 場合があります。ただし、set の 要素の順番 に 意味はない ので、表示される順番 は 重要ではありません。

print("list")
for i in [1, 2, 3]:
    print(i)
print("set")
for i in (1, 2, 3):
    print(i)

実行結果

list
1
2
3
set
1
2
3

インデックスは利用できない

set は、要素の順番 に 意味はない ので、list のように、インデックス を使って 特定の順番の要素 を 取りだしたり、値を変更 することは できません。下記のプログラムのように set に インデックスを記述 して 要素を参照 しようとすると、エラーが発生 します。

a = {1, 2, 3}
print(a[1])

実行結果

---------------------------------------------------------------------------
TypeError                                 Traceback (most recent call last)
Cell In[22], line 2
      1 a = {1, 2, 3}
----> 2 print(a[1])

TypeError: 'set' object is not subscriptable

上記のエラーメッセージは、以下のような意味を持ちます。

TypeError
データ型（Type）に関するエラー
set object is not subscriptable
set は、[] を使ってその中のデータを参照する（subscript）ことはできない（is not able）

set と list の使い分け

ここまでの説明で set と list は 似ている部分が多い と思った方が多いのではないかと思います。実際に set と list は、多くの点 で 似ていますが、下記の点が 大きく異なる ので、状況に応じて 適切に 使い分ける必要 があります。

set は、その 要素の中 に、同じデータ を 複数持つ ことが できない
set の 要素の順番 は 意味を持たない
set の要素を、インデックス を指定して参照することは できない。できるのは、特定の値 が set の 要素の中 に 存在するか どうかを 判定する（帰属判定）ことだけである
set は、要素の 追加と削除 を行うことはできるが、要素の値 を 直接変更できない
set は、ハッシュ可能 なオブジェクト しか扱えない

上記の性質のうち、最後の性質以外 は、数学の 集合の性質 です。従って、set は、複数のデータ を 集合として扱いたい 場合に利用します。具体的には、主に、下記の 1 ～ 3 の 性質を持つ データを 扱う際 に利用します。

下記の いずれか（または複数）の目的で 複数のデータ を 扱いたい
1. 複数のデータ の中に、特定のデータ が 存在するか（帰属関係）を 判定したい
2. 複数のデータどうし が、包含関係 や 相当関係 にあるかを 判定したい
3. 複数のデータどうし の、和集合など の 集合としての演算 を 行いたい
複数のデータ の順番と個数を 扱う必要がない
複数のデータ の内容を後から 変更しない

enum_markpats が計算する、マークのパターン の一覧は、上記の 1-1、2、3 の 性質を満たす データなので、set を使って表現することが できます。

上記の 3 の性質 の意味が 分かりづらい と思いますので補足します。

例えば、enum_markpats によって、マークのパターン の一覧として「自 1 敵 0 空 2」と「自 0 敵 0 空 3」いう 2 つ の マークパターン が計算された場合のことを考えてみて下さい。局面が 変わらなければ、その局面の マークのパターン の一覧は 変わりません。従って、局面が 変わらない限り、マークのパターン の一覧の いずれか を例えば「自 1 敵 1 空 1」のように変更しては いけない ことがわかります。これが、「内容を 後から変更しない」ということの意味です。

従って、逆に下記の いずれか の 性質を 持つ データ を扱いたい場合は、set ではなく、list、tuple、dict などを利用する必要があります。ただし、3 つ目の性質 が 必要な場合 は tuple は 利用できません。

複数のデータ を、順番を付けて 管理したい
同じデータ を 複数個 管理したい
管理するデータ の内容を 後から変更 したい

set がハッシュ可能なオブジェクトしか扱えない理由

set の性質の中で、ハッシュ可能 なオブジェクト しか扱えない という性質が、集合の性質とは 関係ない ように 見える かもしれませんので、この性質 がある理由を説明します。

処理を高速に行うため

set に対して 行うことができる、下記のような set に対して 行うことができる さまざまな演算 では、特定のデータ と set の要素 が 等しいか どうかを 判定する必要 があります。また、ハッシュ可能なオブジェクト は、ハッシュ値 を利用することで、等しいかどうか を、高速に判定 できます。そのため、set の要素を ハッシュ可能なオブジェクト に 限定する ことで、set に関する 多くの処理 を 高速に行う ことが できるようになります。

in 演算による 帰属関係 の判定
比較演算子 による 包含関係、相当関係 の判定
和集合など の set どうし の さまざまな演算

そのことを確認するために、set と list の両方で共通して行うことが できる、in 演算子 による 帰属関係 の判定の 処理速度 を、set と list で比較することにします。

なお、下記の比較 は、ざっくりとした比較 なので、厳密な set と list の 処理速度の比較 には なっていません が、処理速度 の 圧倒的な差 から、要素が多い場合 は、set のほうが list より も高速に 処理を行う ことが できる という事実は間違いなく 確認できます。

下記のプログラムは、0 ~ 100000 未満 の、10 万個 の整数を要素として持つ list と set を 内包表現 を使って作成し、l と s という名前の変数に代入しています。

l = [ i for i in range(100000) ] # 10 万個の要素を持つ list
s = { i for i in range(100000) } # 10 万個の要素を持つ set

次に、下記のプログラムで、0 ~ 100000 未満 の 10 万個 の整数が l の要素に 含まれるか どうかを in 演算子 で判定し、その数を数える という処理を行います。10 万個 の すべて の整数が l に含まれる ので 実行結果 には 10万 が表示されます。筆者のパソコン で、下記のプログラムを実行すると 約 54.6 秒 かかりました。つまり、一回の in 演算子 の判定で、平均するとその 10 万分の 1 の、約 0.546 ミリ秒 の 処理時間 がかかります。

count = 0
for i in range(100000):
    if i in s:
        count += 1
print(count)

実行結果

次に、下記のプログラムで set が代入された s に対して 同じ処理 を行います。筆者のパソコン で、下記のプログラムを実行すると、一瞬で 処理が終 了し、JupyterLab のセルには 0.0 秒 と表示されました。

count = 0
for i in range(100000):
    if i in s:
        count += 1
print(count)

実行結果

あまりに速く 計算が行われてしまったため、JupyterLab の セルの表示 では 処理時間 をうまく 計測できなかった ので、in 演算子 で処理を行う回数を下記のプログラムのように、100 倍 の 1000 万回 行うことにします。なお、s の要素には、10 万まで の整数しか 存在しない ので、下記のプログラムの 3 行目 のように、余りを計算 する % 演算子 を使って i を 10 万で割った余り が s の要素に 存在するか どうかを 計算する ことで、常に s に 要素が存在 する値で in 演算子 の 計算を行う ようにしています。

筆者のパソコン で、下記のプログラムを実行すると 約 1.8 秒 の時間がかかりました。つまり、一回の in 演算子 の判定で、平均するとその 100 万分の 1 の、約 0.0018 ミリ秒 の 処理時間 がかかります。

count = 0
for i in range(10000000):
    if i % 100000 in s:
        count += 1
print(count)

実行結果

10000000

筆者のパソコン では、1 回あたり の in 演算子 の 処理速度 は、list の場合は 約 0.546 ミリ秒、set の場合は、約 0.0018 秒 かかったので、set のほうが 0.546 ÷ 0.0018 = 約 300 倍 の速度で 処理を行う ことができることが分かりました。

このように、ハッシュ可能なオブジェクト に 要素の値 を限定することで、同じ in 演算子 による処理を行った場合でも、list と set では 処理時間 に 大きな差 が 生じます。

要素の数と処理速度の差の関係

なお、詳しい説明は省略しますが、in 演算子 による 処理速度 は、list の場合 は、list の 要素の数 に ほぼ比例 しますが、set の場合 は ほとんど変わりません。例えば、要素の数 を下記のプログラムのように、1/10 の 1 万 に 減らして 先程と 同様の処理 を行ってみます。

l = [ i for i in range(10000) ] # 1 万個の要素を持つ list
s = { i for i in range(10000) } # 1 万個の要素を持つ set

下記のプログラム（3 行目 を i % 10000 に修正しています）を実行すると、筆者のパソコン では、先程の 約 1/10 の 約 5.6 秒 の 処理時間 がかかりました。

count = 0
for i in range(100000):
    if i % 10000 in l:
        count += 1
print(count)

一方、下記のプログラムを実行すると、筆者のパソコン では 約 1.8 秒 かかり、処理時間 が 変わらない 事が分かります。なお、処理時間 の計測は、パソコンの状態 によって 全く同じ計算 を行った場合でも 若干の変化 があります。この例では 処理時間 は 変わりません でしたが、理論的 には set の要素の数 が 少なくなる と 処理時間 も 若干短く なります。

より厳密 な 処理時間 の 計測方法 については、今後の記事 で紹介します。

count = 0
for i in range(10000000):
    if i % 10000 in s:
        count += 1
print(count)

このように、set と list の 処理速度 は、要素の数 が 大きい程、顕著な 差が生じます が、要素の数 が 10 程度 であれば、処理速度 の差は ほとんどありません。実際に、下記のプログラムで、要素の数 が 10 の list と set で 1000 万回 の in 演算子 の 処理時間 を計測した所、list が 約 2.1 秒、set が 約 1.4 秒 となり、処理時間 は あまり変わりません でした。

先程言及したように、要素の数 が 1 万より 大きく 少ない 10 の場合は、set の 処理時間 が、先程の 約 1.8 秒より も 若干短く なっています。

なお、それぞれ の 処理時間 を JupyterLab の セルの表示 で計測するためには、下記の 3 つ のプログラムを 別々のセル で 実行する必要 がある点に注意して下さい。

l = [ i for i in range(10) ] # 10 個の要素を持つ list
s = { i for i in range(10) } # 10 個の要素を持つ set

count = 0
for i in range(10000000):
    if i % 10 in l:
        count += 1
print(count)

count = 0
for i in range(10000000):
    if i % 10 in s:
        count += 1
print(count)

このことから、in 演算子 を使って 帰属判定 を行う際に、set と list の どちら を使っても 良い場合 では、要素の数 が数十を 超える ことが判明した時点で、set を 積極的に利用 したほうが良いことが分かります。

残念ながら、〇×ゲーム の マークのパターン の場合は、最大でも 要素の数 が 8 しかない ので、処理速度 の面では set と list で 大きな差はない でしょう。そのことは、set を利用 するプログラムで ai8s を 修正後 に検証することにします。

set の性質を満たすため

set の性質 に、要素の値 を 変更できない というものがあります。これは、先程のノート で マークのパターン の集合を例に挙げて説明したように、数学の 集合を扱う際 に、一度 集合の要素 に 入れた ものの内容を 後から変更する という処理を 行わない からです。

しかし、set の要素に list のような ハッシュ可能でない、ミュータブル なデータを 代入できてしまう と、set に 対する処理 によって 要素の値 を 変更できなくても、list の要素 を変更することで、間接的 に set の要素 の値を 変更できてしまう ことになります。

下記のプログラムは、実際に 実行するとエラー になりますが、仮に set の要素 に、list を代入できる 場合は、間接的 に set の 要素の値 を 変更できてしまいます。

a = [3, 4, 5] 
b = {1, 2, a} # a は list なので実際にはこの行を実行するとエラーになる
a[0] = 5      # 仮に上記でエラーが発生しない場合は、この処理で、b の要素の値を変更できてしまう

以前の記事で説明したように、ハッシュ可能なオブジェクト であれば、上記のようなことは基本的には 起きない³ので この問題 は 発生しません。

set と list の比較

set と list は 性質が似ている ので、今回の記事で紹介した set の性質 に関して list と比較 したものを下記の表にまとめます。

	list	set
リテラルの外側の記号	`[` と `]` で要素を囲む	`{` と `}` で要素を囲む
リテラルの要素の区切り	`,` で区切る	list と同じ
空のデータ	`[]`	`set()`
内包表記の外側の記号	`[` と `]` で要素を囲む	`{` と `}` で要素を囲む
扱えるのデータの種類	任意のオブジェクト	ハッシュ可能なオブジェクト
要素の順番	順番がある	順番はない
要素の変更	追加、削除、変更	追加、削除のみ
インデックスで参照できるか	可能	不可能
要素に含まれるかの判定	`in`、`not in` 演算子	list と同じ
`==` 演算子での `True` の判定	順番も含めて等しい	同じ要素を持つ
演算子による演算	`+` `*` による結合	`\|` `&` `-` `^` による集合演算
要素の追加のメソッド	`append`	`add`
要素の数を数える組み込み関数	`len`	list と同じ
要素の列挙	for 文により可能	list と同じ

set を使った `ai8s` の実装

set の 使い方 を説明したので、次に、set を使って処理を行うように ai8s を修正します。

`enum_markpats` の修正

ai8s が set を 利用するため には、enum_markpats が 返すデータ を、下記のプログラムのように list から set に修正 する必要があります。set と list は 使い方 が かなり似ている ので、下記の部分だけ を修正するだけで済みます。

2 行目：markpats に代入する値を、空の list から 空の set に修正する
7、9、12、15 行目：append メソッドを、add メソッドに修正する

 1  def enum_markpats(self):
 2      markpats = set()
 3  
 4      # 横方向と縦方向の判定
 5      for i in range(self.BOARD_SIZE):
 6          count = self.count_marks(coord=[0, i], dx=1, dy=0)
 7          markpats.add(count)
 8          count = self.count_marks(coord=[i, 0], dx=0, dy=1)
 9          markpats.add(count)
10      # 左上から右下方向の判定
11      count = self.count_marks(coord=[0, 0], dx=1, dy=1)
12      markpats.add(count)
13      # 右上から左下方向の判定
14      count = self.count_marks(coord=[2, 0], dx=-1, dy=1)
15      markpats.add(count)
16
17      return markpats
18
19  Marubatsu.enum_markpats = enum_markpats

行番号のないプログラム

def enum_markpats(self):
    markpats = set()
 
    # 横方向と縦方向の判定
    for i in range(self.BOARD_SIZE):
        count = self.count_marks(coord=[0, i], dx=1, dy=0)
        markpats.add(count)
        count = self.count_marks(coord=[i, 0], dx=0, dy=1)
        markpats.add(count)
    # 左上から右下方向の判定
    count = self.count_marks(coord=[0, 0], dx=1, dy=1)
    markpats.add(count)
    # 右上から左下方向の判定
    count = self.count_marks(coord=[2, 0], dx=-1, dy=1)
    markpats.add(count)

    return markpats

Marubatsu.enum_markpats = enum_markpats

修正箇所

def enum_markpats(self):
-   markpats = []
+   markpats = set()
 
    # 横方向と縦方向の判定
    for i in range(self.BOARD_SIZE):
        count = self.count_marks(coord=[0, i], dx=1, dy=0)
-       markpats.append(count)
+       markpats.add(count)
        count = self.count_marks(coord=[i, 0], dx=0, dy=1)
-       markpats.append(count)
+       markpats.add(count)
    # 左上から右下方向の判定
    count = self.count_marks(coord=[0, 0], dx=1, dy=1)
-   markpats.append(count)
+   markpats.add(count)
    # 右上から左下方向の判定
    count = self.count_marks(coord=[2, 0], dx=-1, dy=1)
-   markpats.append(count)
+   markpats.add(count)

    return markpats

Marubatsu.enum_markpats = enum_markpats

下記は、前回の記事で enum_markpats の実装を確認する際に記述したプログラムです。このプログラムを実行すると、下記のような エラーが発生 します。

mb = Marubatsu()

print(mb)
pprint(mb.enum_markpats())

mb.move(1, 1)
print(mb)
pprint(mb.enum_markpats())

mb.move(0, 0)
print(mb)
pprint(mb.enum_markpats())

mb.move(1, 0)
print(mb)
pprint(mb.enum_markpats())

実行結果

略
Cell In[33], line 7
      5 for i in range(self.BOARD_SIZE):
      6     count = self.count_marks(coord=[0, i], dx=1, dy=0)
----> 7     markpats.add(count)
      8     count = self.count_marks(coord=[i, 0], dx=0, dy=1)
      9     markpats.add(count)

TypeError: unhashable type: 'collections.defaultdict'

上記のエラーメッセージは、以下のような意味を持ちます。

SyntaxError
データ型（type）に関するエラー
unhashable type: 'collections.defaultdict'
collections モジュールの defaultdict は、ハッシュ可能（hashable）なデータ型（type）ではない（un）

この エラー は、ハッシュ可能でない、defaultdict を set の要素 として追加しようとしたことが原因です。従って、この エラー を修正するためには、ハッシュ可能なオブジェクト を返すように、count_marks を修正する必要があります。

今回の記事のまとめ

長くなりましたので、今回の記事はここまでにし、修正は次回の記事で行うことにします。なお、上記の enum_markpats には バグがある ので、marubatsu.py には 反映させません。

今回の記事では、集合を扱う データ型 である set に関する説明を行いました。また、set を使って ai8s を修正する際に エラーが発生する ことを説明しました。

本記事で入力したプログラム

以下のリンクから、本記事で入力して実行した JupyterLab のファイルを見ることができます。

今回の記事では marubatsu.py と ai.py は変更していません。

次回の記事

違っていれば指摘していただければ嬉しいです ↩
オペランド（operand）とは、演算子 が 演算の対象 とする値のことです ↩ ↩²
正確には、例外として、自分で定義 した クラス の インスタンス の場合は 間接的 にその 属性の値 を 変更できる ので、その点に注意 する必要があります ↩

Pythonで〇×ゲームのAIを一から作成する その52 set の性質と利用方法

目次と前回の記事

これまでに作成したモジュール

これまでに作成した AI

enum_markpats の問題点

集合とは何か

有限集合と無限集合

集合の性質

集合の例

同じ要素が重複しない

集合の要素に順番はない

空集合の例

帰属関係

包含関係と相当関係

集合どうしの演算の例

set の使い方

set の作成

set のリテラル

空の set のリテラル

list からの作成

set 内包表記

set が扱えるデータ

帰属関係の判定

包含関係と相当関係（等しい）の判定

比較演算子の利用例

set どうしの演算

set に対するさまざまな操作

add メソッドによる要素の追加

|= 演算子による要素の追加

|= 演算子に関する注意点

set の内容を更新する他の演算子

要素の削除

要素の数の計算

for 文による要素の列挙

インデックスは利用できない

set と list の使い分け

set がハッシュ可能なオブジェクトしか扱えない理由

処理を高速に行うため

要素の数と処理速度の差の関係

set の性質を満たすため

set と list の比較

set を使った ai8s の実装

enum_markpats の修正

今回の記事のまとめ

本記事で入力したプログラム

次回の記事

Pythonで〇×ゲームのAIを一から作成する　その52　set の性質と利用方法

`enum_markpats` の問題点

`add` メソッドによる要素の追加

`|=` 演算子による要素の追加

`|=` 演算子に関する注意点

set を使った `ai8s` の実装

`enum_markpats` の修正