目次と前回の記事
これまでに作成したモジュール
以下のリンクから、これまでに作成したモジュールを見ることができます。
これまでに作成した AI
これまでに作成した AI の アルゴリズム は以下の通りです。
| ルール | アルゴリズム |
|---|---|
| ルール1 | 左上から順 に 空いているマス を探し、最初に見つかったマス に 着手 する |
| ルール2 | ランダム なマスに 着手 する |
| ルール3 |
真ん中 のマスに 優先的 に 着手 する 既に 埋まっていた場合 は ランダム なマスに 着手 する |
| ルール4 |
真ん中、隅 のマスの 順 で 優先的 に 着手 する 既に 埋まっていた場合 は ランダム なマスに 着手 する |
| ルール5 |
勝てる場合 に 勝つ そうでない場合は ランダム なマスに 着手 する |
| ルール6 |
勝てる場合 に 勝つ そうでない場合は 相手の勝利 を 阻止 する そうでない場合は ランダム なマスに 着手 する |
| ルール6改 |
勝てる場合 に 勝つ そうでない場合は 相手 が 勝利できる 着手を 行わない そうでない場合は ランダム なマスに 着手 する |
| ルール7 |
真ん中 のマスに 優先的 に 着手 する そうでない場合は 勝てる場合 に 勝つ そうでない場合は 相手の勝利 を 阻止 する そうでない場合は ランダム なマスに 着手 する |
| ルール7改 |
真ん中 のマスに 優先的 に 着手 する そうでない場合は 勝てる場合 に 勝つ そうでない場合は 相手 が 勝利できる 着手を 行わない そうでない場合は ランダム なマスに 着手 する |
| ルール8 |
真ん中 のマスに 優先的 に 着手 する そうでない場合は 勝てる場合 に 勝つ そうでない場合は 相手 が 勝利できる 着手を 行わない そうでない場合は、次 の 自分の手番 で 勝利できる ように、「自 2 敵 0 空 1」が 1 つ以上 存在する 局面になる着手を行う そうでない場合は ランダム なマスに 着手 する |
| ルール9 |
真ん中 のマスに 優先的 に 着手 する そうでない場合は 勝てる場合 に 勝つ そうでない場合は 相手 が 勝利できる 着手を 行わない そうでない場合は、次 の 自分の手番 で 必ず勝利できる ように、「自 2 敵 0 空 1」が 2 つ以上存在する 局面になる着手を行う そうでない場合は、次 の 自分の手番 で 勝利できる ように、「自 2 敵 0 空 1」が 1 つ存在する 局面になる着手を行う そうでない場合は ランダム なマスに 着手 する |
| ルール10 |
真ん中 のマスに 優先的 に 着手 する そうでない場合は 勝てる場合 に 勝つ そうでない場合は 相手 が 勝利できる 着手を 行わない そうでない場合は、次 の 自分の手番 で 必ず勝利できる ように、「自 2 敵 0 空 1」が 2 つ以上存在する 局面になる着手を行う そうでない場合は、以下 の 2 つを 総合的に判断 して着手を行う
|
| ルール11 |
真ん中 のマスに 優先的 に 着手 する そうでない場合は 勝てる場合 に 勝つ そうでない場合は 相手 が 勝利できる 着手を 行わない そうでない場合は、次 の 自分の手番 で 必ず勝利できる ように、「自 2 敵 0 空 1」が 2 つ以上存在する 局面になる着手を行う そうでない場合は、以下 の 3 つを 総合的に判断 して着手を行う
|
| ルール12 |
真ん中 のマスに 優先的 に 着手 する そうでない場合は 勝てる場合 に 勝つ そうでない場合は 相手 が 勝利できる 着手を 行わない そうでない場合は、次 の 自分の手番 で 必ず勝利できる ように、「自 2 敵 0 空 1」が 2 つ以上存在する 局面になる着手を行う そうでない場合は、斜め方向 に 〇×〇 が 並び、他の 6 マス が 空のマス の場合に、いずれか の 辺のマス に着手を行う そうでない場合は、以下 の 3 つを 総合的に判断 して着手を行う
|
| ルール12 改 |
相手 が 勝利できる 着手を 行わない そうでない場合は、次 の 自分の手番 で 必ず勝利できる ように、「自 2 敵 0 空 1」が 2 つ以上存在する 局面になる着手を行う そうでない場合は、斜め方向 に 〇×〇 が 並び、他の 6 マス が 空のマス の場合に、いずれか の 辺のマス に着手を行う そうでない場合は、以下 の 3 つを 総合的に判断 して着手を行う
|
ルール 11、12 で 評価値を計算 する際の パラメータ は以下の通りです。
ai11sver 1 |
ai11sver 2 |
ai11s ver 3ai12s
|
|
|---|---|---|---|
| 「自 2 敵 0 空 1」が 1 つの場合の評価値 | 1 | 2 | 2 |
| 「自 1 敵 0 空 2」が 1 つあたりの評価値 | 1 | 1 | 0.5 |
| 「自 0 敵 1 空 2」が 1 つあたりの評価値 | -1 | -1 | 1 |
基準となる ai2 との 対戦結果(単位は %)は以下の通りです。太字 は ai2 VS ai2 よりも 成績が良い 数値を表します。欠陥 の列は、アルゴリズム に 欠陥 があるため、ai2 との 対戦成績 が 良くても強い とは 限らない ことを表します。欠陥の詳細については、関数名のリンク先の説明を見て下さい。
| 関数名 | o 勝 | o 負 | o 分 | x 勝 | x 負 | x 分 | 勝 | 負 | 分 | 欠陥 |
|---|---|---|---|---|---|---|---|---|---|---|
ai1ai1s
|
78.1 | 17.5 | 4.4 | 44.7 | 51.6 | 3.8 | 61.4 | 34.5 | 4.1 | あり |
ai2ai2s
|
58.7 | 28.8 | 12.6 | 29.1 | 58.6 | 12.3 | 43.9 | 43.7 | 12.5 | |
ai3ai3s
|
69.3 | 19.2 | 11.5 | 38.9 | 47.6 | 13.5 | 54.1 | 33.4 | 12.5 | |
ai4ai4s
|
83.0 | 9.5 | 7.4 | 57.2 | 33.0 | 9.7 | 70.1 | 21.3 | 8.6 | あり |
ai5ai5s
|
81.2 | 12.3 | 6.5 | 51.8 | 39.8 | 8.4 | 66.5 | 26.0 | 7.4 | |
ai6 |
88.9 | 2.2 | 8.9 | 70.3 | 6.2 | 23.5 | 79.6 | 4.2 | 16.2 | |
ai6s |
88.6 | 1.9 | 9.5 | 69.4 | 9.1 | 21.5 | 79.0 | 5.5 | 15.5 | |
ai7ai7s
|
95.8 | 0.2 | 4.0 | 82.3 | 2.4 | 15.3 | 89.0 | 1.3 | 9.7 | |
ai8s |
98.2 | 0.1 | 1.6 | 89.4 | 2.5 | 8.1 | 93.8 | 1.3 | 4.9 | |
ai9s |
98.7 | 0.1 | 1.2 | 89.6 | 2.4 | 8.0 | 94.1 | 1.3 | 4.6 | |
ai10s |
97.4 | 0.0 | 2.6 | 85.6 | 2.6 | 11.7 | 91.5 | 1.3 | 7.2 | |
ai11s ver 1 |
98.1 | 0.0 | 1.9 | 82.5 | 1.9 | 15.6 | 90.3 | 1.0 | 8.7 | あり |
ai11s ver 2 |
98.8 | 0.0 | 1.2 | 87.7 | 2.4 | 10.0 | 93.2 | 1.2 | 5.6 | |
ai11s ver 3 |
99.1 | 0.0 | 0.9 | 87.7 | 0.8 | 11.5 | 93.4 | 0.4 | 6.2 | |
ai12s ver 2 |
98.9 | 0.0 | 1.1 | 88.2 | 0.0 | 11.8 | 93.5 | 0.0 | 6.5 | |
ai12s ver 3 |
95.8 | 0.0 | 4.2 | 86.9 | 0.0 | 13.1 | 91.3 | 0.0 | 8.7 | あり |
ai12s ver 2 VS ai2 と ai12s ver 3 VS ai2 の違いの検証
前回の記事では、「勝てる場合 に 勝つ」と、『「自 2 敵 0 空 1」が 2 つ以上存在 する着手を行う』に対する 評価値 に どちらも 200 に 設定 した ai12s ver 3 を作成しましたが、その際に、下記の表のように、ai12s ver 2 VS ai2 と 比較 して、ai12s ver 3 VS ai2 のほうが 引き分け率 が 増えてしまう という バグが発生 することが わかりました。
| 関数名 | o 勝 | o 負 | o 分 | x 勝 | x 負 | x 分 | 勝 | 負 | 分 |
|---|---|---|---|---|---|---|---|---|---|
ai12s ver 2 |
98.9 | 0.0 | 1.1 | 88.2 | 0.0 | 11.8 | 93.5 | 0.0 | 6.5 |
ai12s ver 3 |
95.8 | 0.0 | 4.2 | 86.9 | 0.0 | 13.1 | 91.3 | 0.0 | 8.7 |
また、対戦を検証 することで、ai12s ver 3 の バグの原因 となっている 局面を発見 しました。今回の記事では、最初にその バグの原因 を 検証 します。
下図は、前回の記事で発見した、結果 が 異なる ai12s ver 2 VS ai2 と ai12s ver 3 VS ai2 の 試合経過 を 上下に並べた ものです。
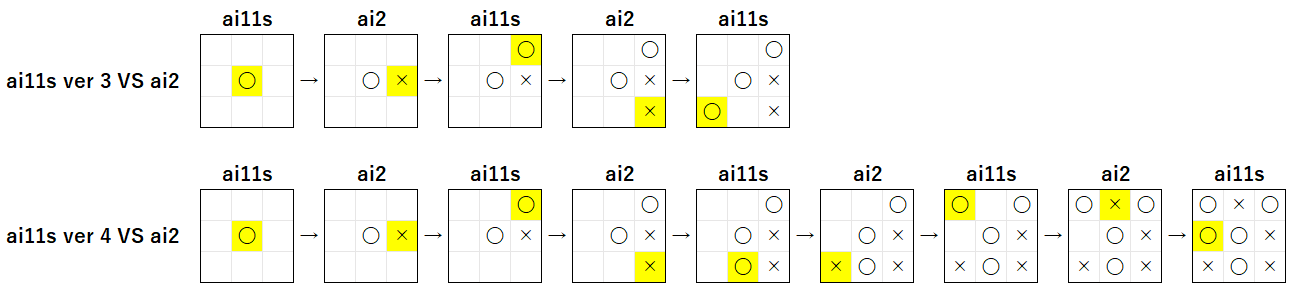
図から、同じ乱数の種 を使っているため、4 手目まで は 同じ着手 が 選択 されていることが わかります。そこで、5 手目以降 の ai12s ver2 と ver 3 の 着手を検討 することにします。なお、ai2 は ランダムな着手 を行う AI なので、ai2 の 着手の検討 は 省略 します。
5 手目の検証

ai12s ver 2 は、「勝てる場合 に 勝つ」という 条件 の 評価値 が 最も高い ので、上記の局面 で (0, 2) に 着手 して 勝利 します。特に難しい点はないでしょう。

次に、ai12s ver 3 が 上記の局面 で 計算 する 評価値 を下記のプログラムで 表示 します。
from marubatsu import Marubatsu
from ai import ai12s
mb = Marubatsu()
mb.move(1, 1)
mb.move(2, 1)
mb.move(2, 0)
mb.move(2, 2)
ai12s(mb, score_victory=200, debug=True)
実行結果(長いのでクリックして開いてください)
Start ai_by_score
Turn o
..o
.ox
..X
legal_moves [(0, 0), (1, 0), (0, 1), (0, 2), (1, 2)]
====================
move (0, 0)
Turn x
O.o
.ox
..x
defaultdict(<class 'int'>,
{Markpat(last_turn=0, turn=1, empty=2): 1,
Markpat(last_turn=1, turn=0, empty=2): 2,
Markpat(last_turn=1, turn=1, empty=1): 1,
Markpat(last_turn=1, turn=2, empty=0): 1,
Markpat(last_turn=2, turn=0, empty=1): 2,
Markpat(last_turn=2, turn=1, empty=0): 1})
score 200 best score -inf
UPDATE
best score 200
best moves [(0, 0)]
====================
move (1, 0)
Turn x
.Oo
.ox
..x
defaultdict(<class 'int'>,
{Markpat(last_turn=0, turn=0, empty=3): 1,
Markpat(last_turn=0, turn=1, empty=2): 1,
Markpat(last_turn=1, turn=1, empty=1): 2,
Markpat(last_turn=1, turn=2, empty=0): 1,
Markpat(last_turn=2, turn=0, empty=1): 3})
score 200 best score 200
APPEND
best moves [(0, 0), (1, 0)]
====================
move (0, 1)
Turn x
..o
Oox
..x
defaultdict(<class 'int'>,
{Markpat(last_turn=0, turn=1, empty=2): 1,
Markpat(last_turn=1, turn=0, empty=2): 3,
Markpat(last_turn=1, turn=1, empty=1): 1,
Markpat(last_turn=1, turn=2, empty=0): 1,
Markpat(last_turn=2, turn=0, empty=1): 1,
Markpat(last_turn=2, turn=1, empty=0): 1})
score 2.5 best score 200
====================
move (0, 2)
winner o
..o
.ox
O.x
score 200 best score 200
APPEND
best moves [(0, 0), (1, 0), (0, 2)]
====================
move (1, 2)
Turn x
..o
.ox
.Ox
defaultdict(<class 'int'>,
{Markpat(last_turn=0, turn=0, empty=3): 1,
Markpat(last_turn=1, turn=0, empty=2): 1,
Markpat(last_turn=1, turn=1, empty=1): 3,
Markpat(last_turn=1, turn=2, empty=0): 1,
Markpat(last_turn=2, turn=0, empty=1): 2})
score 200 best score 200
APPEND
best moves [(0, 0), (1, 0), (0, 2), (1, 2)]
====================
Finished
best score 200
best moves [(0, 0), (1, 0), (0, 2), (1, 2)]
下記は、上記の結果 を まとめた表 です。
| 勝利 | 「201」 | 「021」 | 「102」 | 「012」 | 評価値 | ||
|---|---|---|---|---|---|---|---|
| 評価値 | 200 |
1:+22~: 200
|
-100 |
1 つで+0.5
|
1 つで-1
|
||
| 1 | 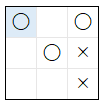 |
2 | 2 | 1 | 200 | ||
| 2 |  |
3 | 1 | 200 | |||
| 3 |  |
1 | 3 | 1 | 2.5 | ||
| 4 | 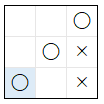 |
1 | 3 | 200 | |||
| 5 |  |
2 | 1 | 200 |
ai12s ver 3 は、「勝てる場合 に 勝つ」と、『「自 2 敵 0 空 1」が 2 つ以上存在 する着手を行う』に対する 評価値 が どちらも 200 に 設定 されており、上記の表 でも そのようになっています。そのため、この局面 では、勝利 する 合法手 4 だけでなく、合法手 1、2、5 の 評価値 も 200 になるため、合法手 1、2、4、5 の 中から ランダムに 選択 が行われることが わかります。そのことは、下記の 実行結果 の 最後の 2 行 からも 確認 できます。
best score 200
best moves [(0, 0), (1, 0), (0, 2), (1, 2)]
「勝てる場合 に 勝つ」と、『「自 2 敵 0 空 1」が 2 つ以上存在 する着手を行う』という 条件 の 評価値 は、ヒューリスティック な 条件より も 優先順位が高い ため、ヒューリスティックな条件 による 評価値 は 考慮されない ので 200 に なります。
従って、上記の局面 では、1 / 4 = 25 % の 確率 で (1, 2) が 選択 されたことが わかります。
7 手目の検証
ai12s ver 3 が、上記の局面 で 計算 する 評価値 を 下記 のプログラムで 表示 します。
mb.move(1, 2)
mb.move(0, 2)
ai12s(mb, score_victory=200, debug=True)
実行結果(長いのでクリックして開いてください)
Start ai_by_score
Turn o
..o
.ox
Xox
legal_moves [(0, 0), (1, 0), (0, 1)]
====================
move (0, 0)
Turn x
O.o
.ox
xox
defaultdict(<class 'int'>,
{Markpat(last_turn=1, turn=1, empty=1): 2,
Markpat(last_turn=1, turn=2, empty=0): 2,
Markpat(last_turn=2, turn=0, empty=1): 2,
Markpat(last_turn=2, turn=1, empty=0): 2})
score 200 best score -inf
UPDATE
best score 200
best moves [(0, 0)]
====================
move (1, 0)
winner o
.Oo
.ox
xox
score 200 best score 200
APPEND
best moves [(0, 0), (1, 0)]
====================
move (0, 1)
Turn x
..o
Oox
xox
defaultdict(<class 'int'>,
{Markpat(last_turn=1, turn=0, empty=2): 1,
Markpat(last_turn=1, turn=1, empty=1): 2,
Markpat(last_turn=1, turn=2, empty=0): 2,
Markpat(last_turn=2, turn=0, empty=1): 1,
Markpat(last_turn=2, turn=1, empty=0): 2})
score 2.5 best score 200
====================
Finished
best score 200
best moves [(0, 0), (1, 0)]
下記は、上記の結果 を まとめた表 です。
| 勝利 | 「201」 | 「021」 | 「102」 | 「012」 | 評価値 | ||
|---|---|---|---|---|---|---|---|
| 評価値 | 200 |
1:+22~: 200
|
-100 |
1 つで+0.5
|
1 つで-1
|
||
| 1 | 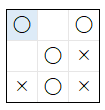 |
2 | 200 | ||||
| 2 |  |
1 | 1 | 1 | 200 | ||
| 3 |  |
1 | 1 | 2.5 |
上記 から、合法手 1、2 の 評価値 が 200 で 最も高い ので、その中 から 合法手が選択 されることが わかります。そのことは、下記の 実行結果 の 最後の 2 行 からも 確認 できます。
best score 200
best moves [(0, 0), (1, 0)]
従って、上記の局面 は、1 / 2 = 50 % の 確率 で (0, 0) が 選択 されたことが わかります。
8 手目以降の検証
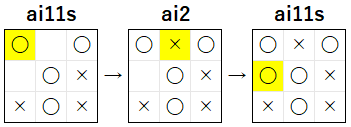
上記は、8 手目以降 の 図 ですが、7 手目 で ai12s ver 3 が、『「自 2 敵 0 空 1」が 2 つ以上存在 する着手を行う』という 条件を満たす、必勝の局面 での 最善手 を 選択 したにもかかわらず、引き分け に なっています。何故このようなことが起こったかについて少し考えてみて下さい。
上記の ai2 が 8 手目 で 着手 した (1, 0) は、1 回 の 着手 で、2 つ ある「自 2 敵 0 空 1」の マークのパターン を 同時 に 無くしています。これが、引き分け になる 原因 です。
このことから、『「自 2 敵 0 空 1」が 2 つ以上存在 する着手を行う』という 条件 は、実は 必勝の局面 での 最善手 を 選択 するための 十分条件 ではなかった ことが わかります。
この条件 の 問題点 は、一度 の 相手の着手 で、複数 の「自 2 敵 0 空 1」の マークのパターン が 同時になくなる 場合があることですが、そのようなことが起きるのは、複数 の「自 2 敵 0 空 1」の マークのパターン の中の 空のマス が 1 つ で 共通している ような 場合 です。
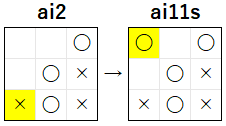
図で説明 すると、下図 の 7 手目 の局面では、「自 2 敵 0 空 1」の マークのパターン が 黄色い行 と オレンジの列 の 2 つ が あります が、それぞれの マークのパターン の中の 空のマス は、緑 の (0, 1) の マス で 共通 しており、1 つ しかありません。この場合は、相手 が 緑のマス に 着手 を行うことで、「自 2 敵 0 空 1」の マークのパターン が 無くなります。
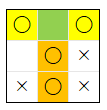
従って、この条件 を 必勝の局面 で 最善手 を 選択 するための 十分条件にする ためには、下記 の 2 つ目 の 条件 を 加える ように 修正 する 必要 が あります。
- 「自 2 敵 0 空 1」が 2 つ以上存在 する着手を行う
- ただし、それらの マークのパターン の中の 空のマス が、2 つ以上存在 する
ところで、ai12s ver 2 と ai12s ver 3 は、どちらもルール 12 の 条件 で 合法手 を 選択 していますが、ルール 12 には、上記 の「それらの マークのパターン の中の 空のマス が、2 つ以上存在 する」という 条件 は 存在しません。それにもかかわらず、ai12s ver 2 VS ai2 では、上図のような、問題 のある 局面 は 出現しません。
その 理由 について 検証 してみた所、ai12s ver 2 が『「自 2 敵 0 空 1」が 2 つ以上存在 する着手』を 行った場合 に、上記 の 2 つ目 の「それらの マークのパターン の中の 空のマス が、2 つ以上存在 する」という 条件 を 必ず満たす ことが 判明 しました。
次は、そのようなことがおきる 理由 について 説明 します。
ai12s ver 2 が条件を満たす理由
ai12s ver 2 が『「自 2 敵 0 空 1」が 2 つ以上存在 する着手』を 行った場合 に、上記 の 2 つ目の条件 を 必ず満す ことを 示す ための 方法の一つ に、ai12s ver 2 が 上記の条件 に 反する、下記 のような 合法手 を 選択しない ことを 示す という 方法 が あります。
- 「自 2 敵 0 空 1」が 2 つ以上存在 する着手を行う
- ただし、それらの マークのパターン の中の 空のマス が、1 つだけ存在 する
下記は、上記の条件 を満たす ai12s ver 3 VS ai2 の 7 手目 を 選択 した 局面 です。緑色 のマスが、「自 2 敵 0 空 1」の マークのパターン で、1 つ だけ 存在 する 空のマス です。

〇×ゲーム は、一度 の 手番 で、一つのマス にしか 着手 を行えない ゲーム なので、上記の局面 の、1 つ前 の 〇 の手番 である 5 手目 の 局面 では、4 つ ある 〇 のマーク の中の、いずれか 1 つ が 配置されていない状態 になっています。そのため、1 つ前 の 〇 の手番 の 局面 は、以下 の いずれか に なります。
- 黄色 の マス の いずれか 1 つ の 〇 が 配置されていない
- オレンジ の マス の いずれか 1 つ の 〇 が 配置されていない
上記 の いずれの場合 であったとしても、1 つ前 の 〇 の手番 の 局面 では、他の色 の 2 つのマス に 〇 が配置 されています。また、緑のマス も、必ず 空のマス なので、1 つ前 の 〇 の手番 の 局面 では、必ず「自 2 敵 0 空 1」が 1 つ存在 することになります。
実際 に、先程の ai12s ver 2 VS ai2 の 5 手目 の局面では、(0, 0) の マス が 空いています が、オレンジ色 の 列 に「自 2 敵 0 空 1」が 1 つ存在 します。

下記 のような 条件 を満たす 合法手を選択 するためには、上図 の 局面 で (0, 0) に 着手 を 行う必要 が あります。
- 「自 2 敵 0 空 1」が 2 つ以上存在 する着手を行う
- ただし、それらの マークのパターン の中の 空のマス が、1 つだけ存在 する
ai12s ver 2 は、「勝てる場合 に 勝つ」という 条件 が 最も優先順位 が 高い ので、上図の局面 では 必ず (0, 1) に 着手 して 勝利 します。従って、ai12s ver 2 が 合法手 を 選択 する場合に、上記 のような 条件 を満たす 合法手 を 選択 することは ありません。
上記 から、以下 の事が わかります。
- 『「自 2 敵 0 空 1」が 2 つ以上存在 する着手を行う』という 条件だけ では、必勝の局面 で 最善手 を 選択 するための 十分条件 には ならない
- 「勝てる場合 に 勝つ」という 条件 を、上記の条件 よりも 優先順位 を 高くする ことで、上記の条件 が 十分条件 に なる
ai12s ver 3 は、上記 の 条件 を 満たさない ため、先程の 7 手目 の局面のように、ai12s ver 2 が 最善手 を 必ず選択 する 局面 で、最善手 を 選択できず に 引き分け に なる場合 が あります。これが、ai12s ver 2 VS ai2 と 比較 して、ai12s ver 3 VS ai2 のほうが 引き分け率 が 増えてしまう という バグ の 原因 です。
なお、ai12s ver 2 が、上記 で 説明 した 理由 から、必勝の局面 で 最善手 を 選択 するための 十分条件 になっていることは、筆者 も 想定しておらず、前回の記事で ai12s ver 3 の 問題 が 見つかるまで は、『「自 2 敵 0 空 1」が 2 つ以上存在 する着手を行う』という 条件だけ で、十分条件 に なっている と 勘違い していました。そのため、ai12s ver 2 が 必勝の局面 で 最善手 を 必ず選択 するように なっていた のは、単なる偶然 に すぎません。
このように、ルールベースの AI では、正しい と 思っていた条件 が 実は 正しくなかった ということが 良くあります。そのため、作成した AI による 対戦 が 意図通り の 結果 に ならなかった場合 は、プログラム だけでなく、ルール の 条件 を 見直す必要 がある 場合がある ことを 忘れない ようにして下さい。
ルール 12 の、「相手 が 勝利できる 着手を 行わない」という 条件 が『「自 2 敵 0 空 1」が 2 つ以上存在 する着手を行う』という 条件より も 優先順位 が 高い ことは、上記と 同じ ような 意味 を 持ちます。もし、「相手 が 勝利できる 着手を 行わない」という 条件 の 優先順位 を 低くしてしまう と、次 の 相手の手番 で 相手 が 勝利 してしまう 可能性が生じる からです。
従って、厳密 には、先程の 必勝の局面 で 最善手 を 選択 するための 十分条件 は 以下 のようになります。
- 「自 2 敵 0 空 1」が 2 つ以上存在 する着手を行う
- ただし、「勝てる場合 に 勝つ」や「相手 が 勝利できる 着手を 行わない」という 条件 を 優先 する
なお、記述 が 長くなる ので、「相手 が 勝利できる 着手を 行わない」という 条件の記述 は 以後 も 省略 することにします。
2 つの十分条件の違い
下記は、最初に紹介した 必勝の局面 で 最善手 を 選択 するための 十分条件 です。
- 「自 2 敵 0 空 1」が 2 つ以上存在 する着手を行う
- ただし、それらの マークのパターン の中の 空のマス が、2 つ以上存在 する
一方、下記の条件 を 満たした場合 に、上記の条件 が 満たされる ので、下記の条件 も、必勝の局面 で 最善手 を 選択 するための 十分条件 であると言えます。
- 「自 2 敵 0 空 1」が 2 つ以上存在 する着手を行う
- ただし、「勝てる場合 に 勝つ」という 条件 を 優先 する1
このように、同じ問題 に対して、その 問題を解決 するための 異なる十分条件 が 考えられる ことが あります が、そのような場合は、どちらの十分条件 を使っても 構わない ので、使いやすい ほうを 利用 すると 良いでしょう。
例えば、ai12s ver 2 は、上記の 後者 の 十分条件 を 利用 していますが、「勝てる場合 に 勝つ」という 条件 を 優先する処理 は、簡単 に 記述できます。
一方、前者 の 十分条件 の、「それらの マークのパターン の中の 空のマス が、2 つ以上存在 する」という 条件 を 利用 して 最善手を選択 することも でき、そちらの場合には、下記 のような 利点 と 欠点 があります。
利点
- 「勝てる場合 に 勝つ」場合と、『「自 2 敵 0 空 1」が 2 つ以上存在 する着手を行う』場合の 評価値 に 同じ値 を 設定 しても、
ai12sver 3 のような 問題 は 発生しない
欠点
- 「自 2 敵 0 空 1」の マークのパターン の中の 空のマス の 数を数える プログラムの 記述 はそれほど 簡単ではなく、処理 が 複雑になる ため 処理時間 が 長く なる
なお、この後で説明しますが、それぞれの 評価値 に 同じ値 を 設定 すると 別の問題 が 発生する ことになるため、上記の利点 はあまり 有効 では ありません。そのため、本記事 では 前者の十分条件 によるプログラムは 記述しない ことにします。興味と時間がある方は、実際にプログラムを記述してみると良いでしょう。
ai12s ver 2 と ai12s ver 3 の優劣
ai12s ver 3 には、上記 で 説明 したような 問題点 がありますが、ランダムな AI に対する 敗率 が 0 % であることから、弱解決の AI であることには 変わりはありません。
このような 問題点 があるにも 関わらず、ai12s ver 3 が 弱解決の AI である 理由 は、〇×ゲーム が 引き分けのゲーム だからです。以前の記事で説明したように、引き分けのゲーム での 弱解決の AI は、必勝の局面 では、必敗の局面 につながる 合法手 を 選択しない という 制約しかない ので、最善手ではない、引き分け に つながる合法手 を 選択 しても かまいません。先ほどの 7 手目 の 局面 では、ai12s ver3 は、必勝の局面 で、最善手ではない、引き分け につながる 合法手 を 選択 しているので、弱解決の AI の 条件 を 満たしています。
弱解決の AI は 自分の必勝のゲーム では、最強の AI と 同じ強さ を持ちますが、そうでない 場合は、このように、弱解決の AI どうし の中で、優劣 は 存在 します。実際に、ai12s ver 2 より も、ai12s ver 3 のほう が、最強の AI に 近い AI です。従って、本記事 では ai12s ver 3 の パラメータ は 採用しない ことにします。
必勝の局面での最善手の優劣
下記の 2 つの条件 は、いずれも、必勝の局面 で 最善手 を 選択 するための 十分条件 です。
- 勝てる場合 に 勝つ
- 「自 2 敵 0 空 1」の マークのパターン が 2 つ以上存在 し、それらの マークのパターン の中の 空のマス が、2 つ以上存在 する 合法手 を 選択 する
従って、それらの 条件 を満たす 合法手 が 両方存在 する場合は、その どちらを選択 しても、AI の強さ という 観点 からは、強さ は 変わりません。
しかし、AI と 人間 が 対戦 する場合に、人間にとって、一般的 に どちらの最善手 が 好ましく思えるか という 観点 では、この 2 種類 の 最善手 は 異なります。
人間にとって最善手に違いが生じる例
具体例 を示します。下図 の 〇 の手番 の 局面 では、黄色 の (2, 2) に 着手 すると 〇 が勝利 するので、(2, 2) は 最善手 です。また、オレンジ の 4 つ のマスのどこに 着手 を行っても、『「自 2 敵 0 空 1」の マークのパターン の中の 空のマス が、2 つ以上存在 する』ので、それらも 最善手 です。つまり、この局面 では すべて の 合法手 が 最善手 です。
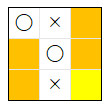
ai12s ver 2 は、「勝てる場合 に 勝つ」という 条件 が 優先される ので、(2, 2) のみ を 選択 します。そのことは、下記 のプログラムの 実行結果 の 最後の行 からも 確認できます。
mb = Marubatsu()
mb.move(1, 1)
mb.move(1, 0)
mb.move(0, 0)
mb.move(1, 2)
ai12s(mb, debug=True)
実行結果の 最後の行
best moves [(2, 2)]
実行結果全体(長いのでクリックして開いてください)
Start ai_by_score
Turn o
ox.
.o.
.X.
legal_moves [(2, 0), (0, 1), (2, 1), (0, 2), (2, 2)]
====================
move (2, 0)
Turn x
oxO
.o.
.x.
defaultdict(<class 'int'>,
{Markpat(last_turn=0, turn=1, empty=2): 1,
Markpat(last_turn=1, turn=0, empty=2): 3,
Markpat(last_turn=1, turn=2, empty=0): 1,
Markpat(last_turn=2, turn=0, empty=1): 2,
Markpat(last_turn=2, turn=1, empty=0): 1})
score 200 best score -inf
UPDATE
best score 200
best moves [(2, 0)]
====================
move (0, 1)
Turn x
ox.
Oo.
.x.
defaultdict(<class 'int'>,
{Markpat(last_turn=0, turn=0, empty=3): 1,
Markpat(last_turn=0, turn=1, empty=2): 1,
Markpat(last_turn=1, turn=0, empty=2): 1,
Markpat(last_turn=1, turn=1, empty=1): 1,
Markpat(last_turn=1, turn=2, empty=0): 1,
Markpat(last_turn=2, turn=0, empty=1): 3})
score 200 best score 200
APPEND
best moves [(2, 0), (0, 1)]
====================
move (2, 1)
Turn x
ox.
.oO
.x.
defaultdict(<class 'int'>,
{Markpat(last_turn=0, turn=1, empty=2): 1,
Markpat(last_turn=1, turn=0, empty=2): 3,
Markpat(last_turn=1, turn=1, empty=1): 1,
Markpat(last_turn=1, turn=2, empty=0): 1,
Markpat(last_turn=2, turn=0, empty=1): 2})
score 200 best score 200
APPEND
best moves [(2, 0), (0, 1), (2, 1)]
====================
move (0, 2)
Turn x
ox.
.o.
Ox.
defaultdict(<class 'int'>,
{Markpat(last_turn=0, turn=0, empty=3): 1,
Markpat(last_turn=1, turn=0, empty=2): 1,
Markpat(last_turn=1, turn=1, empty=1): 2,
Markpat(last_turn=1, turn=2, empty=0): 1,
Markpat(last_turn=2, turn=0, empty=1): 3})
score 200 best score 200
APPEND
best moves [(2, 0), (0, 1), (2, 1), (0, 2)]
====================
move (2, 2)
winner o
ox.
.o.
.xO
score 300 best score 200
UPDATE
best score 300
best moves [(2, 2)]
====================
Finished
best score 300
best moves [(2, 2)]
一方、2 種類 の 最善手 の 評価値 が 同じ である ai12s ver 3 の場合は、すべての合法手 の 評価値 が 同じ値 になる2ので、すべての合法手 の中から ランダム に 選択 が行われます。そのことは、下記 のプログラムの 実行結果 の 最後の行 からも 確認できます。
ai12s(mb, score_victory=200, debug=True)
from ai import ai12s
from marubatsu import Marubatsu
mb = Marubatsu()
mb.move(1, 1)
mb.move(1, 0)
mb.move(0, 0)
mb.move(1, 2)
ai12s(mb, debug=True)
実行結果の 最後の行
best moves [(2, 0), (0, 1), (2, 1), (0, 2), (2, 2)]
実行結果全体(長いのでクリックして開いてください)
Start ai_by_score
Turn o
ox.
.o.
.X.
legal_moves [(2, 0), (0, 1), (2, 1), (0, 2), (2, 2)]
====================
move (2, 0)
Turn x
oxO
.o.
.x.
defaultdict(<class 'int'>,
{Markpat(last_turn=0, turn=1, empty=2): 1,
Markpat(last_turn=1, turn=0, empty=2): 3,
Markpat(last_turn=1, turn=2, empty=0): 1,
Markpat(last_turn=2, turn=0, empty=1): 2,
Markpat(last_turn=2, turn=1, empty=0): 1})
score 200 best score -inf
UPDATE
best score 200
best moves [(2, 0)]
====================
move (0, 1)
Turn x
ox.
Oo.
.x.
defaultdict(<class 'int'>,
{Markpat(last_turn=0, turn=0, empty=3): 1,
Markpat(last_turn=0, turn=1, empty=2): 1,
Markpat(last_turn=1, turn=0, empty=2): 1,
Markpat(last_turn=1, turn=1, empty=1): 1,
Markpat(last_turn=1, turn=2, empty=0): 1,
Markpat(last_turn=2, turn=0, empty=1): 3})
score 200 best score 200
APPEND
best moves [(2, 0), (0, 1)]
====================
move (2, 1)
Turn x
ox.
.oO
.x.
defaultdict(<class 'int'>,
{Markpat(last_turn=0, turn=1, empty=2): 1,
Markpat(last_turn=1, turn=0, empty=2): 3,
Markpat(last_turn=1, turn=1, empty=1): 1,
Markpat(last_turn=1, turn=2, empty=0): 1,
Markpat(last_turn=2, turn=0, empty=1): 2})
score 200 best score 200
APPEND
best moves [(2, 0), (0, 1), (2, 1)]
====================
move (0, 2)
Turn x
ox.
.o.
Ox.
defaultdict(<class 'int'>,
{Markpat(last_turn=0, turn=0, empty=3): 1,
Markpat(last_turn=1, turn=0, empty=2): 1,
Markpat(last_turn=1, turn=1, empty=1): 2,
Markpat(last_turn=1, turn=2, empty=0): 1,
Markpat(last_turn=2, turn=0, empty=1): 3})
score 200 best score 200
APPEND
best moves [(2, 0), (0, 1), (2, 1), (0, 2)]
====================
move (2, 2)
winner o
ox.
.o.
.xO
score 200 best score 200
APPEND
best moves [(2, 0), (0, 1), (2, 1), (0, 2), (2, 2)]
====================
Finished
best score 200
best moves [(2, 0), (0, 1), (2, 1), (0, 2), (2, 2)]
人間の心理を考慮に入れた最善手の優劣
ところで、人間 どうし が 〇×ゲーム で 対戦 する際に、下図の局面 で、相手 が オレンジ色 のマスに 着手 を行った場合、おそらく 多くの人 は、その場で すぐに勝てる局面なのに、わざわざ別の合法手を選択して 勝負を引き延ばされた と思い、気分が悪くなる人 が 多い のではないでしょうか3。人間どうし の対戦では、このような、勝利が確定 している局面で 勝負を引き延ばす ような 行為 の事を、なぶり殺し や、舐めプ(相手を 舐めたプレイ の 略)などと呼び、一般的 には マナーが悪い行為 だと考えられています4。また、そのような行為を行うと、場合によっては 喧嘩に発展する ことも あります。

先程示したように、ai12s ver 2 は、上記の局面 で 必ず黄色 のマスに 着手 を行って 勝利します が、ai12s ver 3 は オレンジ色 のマスに 着手 をする 可能性 が あります。ai12s ver 3 は、決められたルール に従って 着手を選択 しているだけなので、相手 を 侮辱する意図 は ありません し、先程も述べたように、相手に勝利する という 意味 では、どの最善手 を 選択 しても 同じ結果 になりますが、相手 が AI であると わかっていても、そのような着手 を行う AI と 対戦 した際に、多くの人間 は 気分を害する のではないかと思います。
このように、人間 には 感情がある ため、人間と対戦 することを 想定した AI を 作成する場合 は、勝負を引き延ばす ような 最善手 を 選択しない ようにしたほうが 良いでしょう。そのためには、勝負を長引かせない ような 最善手 に 高い評価値 を 設定する ことに 大きな意味 が 生じます。なお、AI どうし でしか 対戦 を 行わない のであれば、そのようなことを 気にする必要 は ありません。
本記事では、作成した AI と 人間 が 対戦 することも 想定 しているので、そのような意味でも、ai12s ver 3 を採用せずに、ai12s ver 2 のほうを 採用する ことにします。
必敗の局面での最善手の優劣
以前の記事で説明したように、必敗の局面 では、すべての合法手 が 最善手 になりますが、それらの合法手 に 優劣 は 存在するでしょうか?その点について少し考えてみて下さい。
相手 が 最強の AI の場合は、必敗の局面 の 合法手 に 優劣 は ありません が、相手 が 最強の AI でない 場合は、優劣 が 存在 します。例えば、下図 の × の手番 の 局面 は、次 の 相手の手番 で オレンジ色 の いずれか に 着手 を行うと 相手が勝利 するので、必敗の局面 です。
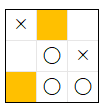
従って、相手 が 最強の AI の場合は、この局面 で × が どの合法手 を 選択 しても、敗北する ので、結果 は 変わりません。実際 に ai12s ver 2 は、下記 のプログラムの 実行結果 の 最後の行 からわかるように、すべての合法手 の中から ランダム に 選択 を 行います。
mb.restart()
mb.move(1, 1)
mb.move(0, 0)
mb.move(2, 2)
mb.move(2, 1)
mb.move(1, 2)
ai12s(mb, debug=True)
実行結果の 最後の行
best moves [(1, 0), (2, 0), (0, 1), (0, 2)]
実行結果全体(長いのでクリックして開いてください)
Start ai_by_score
Turn x
x..
.ox
.Oo
legal_moves [(1, 0), (2, 0), (0, 1), (0, 2)]
====================
move (1, 0)
Turn o
xX.
.ox
.oo
defaultdict(<class 'int'>,
{Markpat(last_turn=0, turn=1, empty=2): 1,
Markpat(last_turn=0, turn=2, empty=1): 1,
Markpat(last_turn=1, turn=0, empty=2): 1,
Markpat(last_turn=1, turn=1, empty=1): 2,
Markpat(last_turn=1, turn=2, empty=0): 2,
Markpat(last_turn=2, turn=0, empty=1): 1})
score -100 best score -inf
UPDATE
best score -100
best moves [(1, 0)]
====================
move (2, 0)
Turn o
x.X
.ox
.oo
defaultdict(<class 'int'>,
{Markpat(last_turn=0, turn=2, empty=1): 2,
Markpat(last_turn=1, turn=0, empty=2): 1,
Markpat(last_turn=1, turn=1, empty=1): 2,
Markpat(last_turn=1, turn=2, empty=0): 1,
Markpat(last_turn=2, turn=0, empty=1): 1,
Markpat(last_turn=2, turn=1, empty=0): 1})
score -100 best score -100
APPEND
best moves [(1, 0), (2, 0)]
====================
move (0, 1)
Turn o
x..
Xox
.oo
defaultdict(<class 'int'>,
{Markpat(last_turn=0, turn=1, empty=2): 1,
Markpat(last_turn=0, turn=2, empty=1): 2,
Markpat(last_turn=1, turn=0, empty=2): 1,
Markpat(last_turn=1, turn=1, empty=1): 1,
Markpat(last_turn=1, turn=2, empty=0): 1,
Markpat(last_turn=2, turn=0, empty=1): 1,
Markpat(last_turn=2, turn=1, empty=0): 1})
score -100 best score -100
APPEND
best moves [(1, 0), (2, 0), (0, 1)]
====================
move (0, 2)
Turn o
x..
.ox
Xoo
defaultdict(<class 'int'>,
{Markpat(last_turn=0, turn=2, empty=1): 1,
Markpat(last_turn=1, turn=0, empty=2): 1,
Markpat(last_turn=1, turn=1, empty=1): 3,
Markpat(last_turn=1, turn=2, empty=0): 2,
Markpat(last_turn=2, turn=0, empty=1): 1})
score -100 best score -100
APPEND
best moves [(1, 0), (2, 0), (0, 1), (0, 2)]
====================
Finished
best score -100
best moves [(1, 0), (2, 0), (0, 1), (0, 2)]
ランダムな AI と対戦する場合の、必敗の局面での最善手の優劣の検証
一方、相手 が 最強の AI でない 場合は、× が 下図 の 5 手目 の 局面 で、それぞれ の 合法手 を 選択 した場合の 勝率 は 異なります。実際 に、それぞれ の 合法手 を 選択 した際に、ランダムな AI である ai2s と 対戦 した場合の 勝率 を 検証する ことにします。ただし、7 手目 の 局面 では、× は 最善手を選択する ものとします。
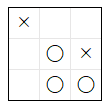
5 手目で (1, 0) に着手した場合

上図左 は、5 手目 で × が (1, 0) に 着手 した場合の 局面 です。この局面 で、〇 を担当 する ai2 は、1/3 の 確率 で 上図の合法手 を 選択 します。その後、× が 最善手 を 選択 すると、上図 のような 結果 に なります。
5 手目で (2, 0) に着手した場合

上図左 は、5 手目 で × が (2, 0) に 着手 した場合の 局面 です。この局面 で、〇 を担当 する ai2 は、1/3 の 確率 で 上図の合法手 を 選択 します。その後、× が 最善手 を 選択 すると、上図 のような 結果 に なります。
5 手目で (0, 1) に着手した場合

上図左 は、5 手目 で × が (0, 1) に 着手 した場合の 局面 です。この局面 で、〇 を担当 する ai2 は、1/3 の 確率 で 上図の合法手 を 選択 します。その後、× が 最善手 を 選択 すると、上図 のような 結果 に なります。
5 手目で (0, 2) に着手した場合
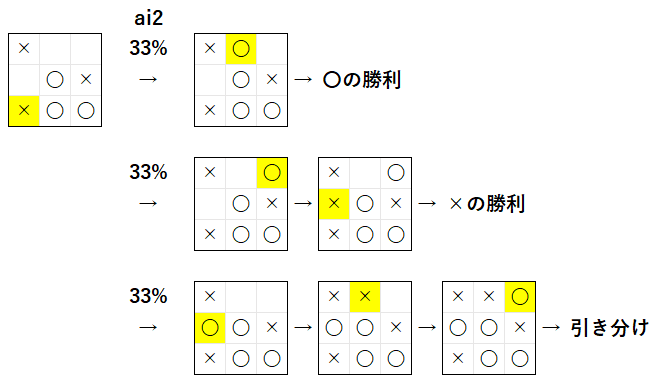
上図左 は、5 手目 で × が (0, 2) に 着手 した場合の 局面 です。この局面 で、〇 を担当 する ai2 は、1/3 の 確率 で 上図の合法手 を 選択 します。その後、× が 最善手 を 選択 すると、上図 のような 結果 に なります。
5 手目の合法手のまとめ
下記 は、上記 の 5 手目 の それぞれの合法手 を 選択 した場合の 勝率 を まとめた表 です5。表から、選択 した 合法手 によって、敗率 と 引き分け率 が 変化 し、この場合は 合法手 1、4 の、(1, 0) と (0, 2) を 選択 したほうが 通算成績 が 良い ことが わかります。
| 勝率 | 敗率 | 引分率 | ||
|---|---|---|---|---|
| 1 |  |
33 % | 33 % | 33 % |
| 2 | 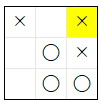 |
33 % | 66 % | 0 % |
| 3 |  |
33 % | 66 % | 0 % |
| 4 | 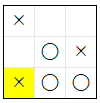 |
33 % | 33 % | 33 % |
5 手目 のそれぞれの 合法手の違い は、その後 の 相手の選択 によって、出現 する 局面の状況 が 異なる 点にあります。例えば、合法手 1、4 は、相手 の 選択次第 で、引き分け になる 可能性 が 生じます が、合法手 2、3 では そのような可能性 は 生じません。
人間からみた 5 手目の合法手の違い

上図の局面 は、ai12s ver 2 から見ると 必敗の局面 なので、どの合法手 を 選択 しても 結果 は 変わらない と 判断 して すべての合法手 の中から ランダム に 選択 します。しかし、〇×ゲーム にある程度以上 親しんだ人 であれば、上記 の 必敗の局面 でも あきらめず に、相手 が 勝利 できる 合法手を減らす ことができる、(1, 0) や (0, 2) を 選択する のではないかと思います。また、この局面 で ai12s ver 2 が例えば (2, 0) に 着手 を 行った場合 に、人間から見る と、AI が ゲームを投げ出したよう に 感じられる人 が多いかもしれません。
上記 の 局面 で、人間から みて 最善を尽くす ように 見える、(1, 0) や (0, 2) を AI が 選択する ようにするための 方法 について少し考えてみて下さい。
最善手の中の優劣の計算方法
評価値 を 利用 する アルゴリズム で、必敗の局面 での、最善手 に 優劣をつける 方法は、もちろん、それぞれ の 合法手 の 評価値 を 異なる値にする ことです。そのため には、必敗の局面 の 合法手 の 評価値 を どのような計算 で 異なる値にするか を 考える必要 があるので、少し考えてみて下さい。
ルール 13 の定義
現状 の ai12s ver 2 は、「自 0 敵 2 空 1」の マークのパターン が 1 つ以上 存在する 局面 に対して 必敗の局面 であると 判断 し、-100 という 評価値 を 計算 していますが、「自 0 敵 2 空 1」の マークのパターン の 数 が 多い程、相手 が 勝ちやすい と 考えること が できます。そこで、「自 0 敵 2 空 1」の マークのパターン の 数 に対して、その数 が 大きい ほうが 評価値 が 小さくなる ように 評価値 を 計算 するという 方法 が 考えられます。
そのような方法 で 評価値 を 計算 することで、「自 0 敵 2 空 1」の マークのパターン の 数 が多ければ 多い程、評価値 が 低くなる ため、選択されづらく なります。
下記は、上記 を ルール 12 改 に 加えた、ルール 13 の 定義 です。具体的には、優先順位 が 2 の 条件 に『ただし、「自 0 敵 2 空 1」の 数 が 少ない着手 を 優先 する』を 加えました。
| 順位 | 条件 | 種類 |
|---|---|---|
| 1 | 勝てる場合 に 勝つ | 十分条件 |
| 2 |
相手 が 勝利できる 着手を 行わない ただし、「自 0 敵 2 空 1」の 数 が 少ない着手 を 優先 する |
必要条件 |
| 3 | 「自 2 敵 0 空 1」が 2 つ以上存在 する着手を行う | 十分条件 |
| 4 |
斜め方向 に 〇×〇 が 並び、他の 6 マス が 空のマス の 場合は、いずれか の 辺のマス に着手を行う |
十分条件 |
| 5 | 「自 2 敵 0 空 1」が 1 つ存在 する着手を行う 「自 1 敵 0 空 2」が 最も多い 着手を行う 「自 0 敵 1 空 2」が 最も少ない 着手を行う |
|
| 6 | ランダム なマスに 着手 する |
評価値の設定
次に、ルール 13 の、相手 が 勝利できる場合 の 評価値 を 計算する方法 を 考える必要 があります。その方法としては、下記 のような 方法 が 考えられます。
- 「自 0 敵 2 空 1」の マークのパターン の 数 を $z$ とした場合で、$z$ が 1 以上 の場合に 評価値 を $-100 × z$ という 式 で 計算 する
他 にも、$-100 - 10 × z$ など、さまざまな式 が 考えられます。本記事 が 採用する式より も ふさわしい と思われる 式があれば、そちらを採用 しても 構いません。
なお、上記 では $-100 × z$ という 式 で 評価値を計算 しましたが、$z$ に 乗算 する パラメータ には、下記 のような 条件 があります。
- 負の値 である
- 計算 された 評価値 の 範囲 が、他 の 優先順位 の 評価値 の 範囲 と 重ならない
下記は、そのこと を 確認 するために、それぞれ の 優先順位 に対する 評価値 の 範囲 を まとめた表 です。表 から、それぞれ の 優先順位 で 計算 される 評価値 の 範囲 が 重複していない ことが 確認 できます。
| 順位 | 局面の状況 | 個別 | 評価値 |
|---|---|---|---|
| 1 | 自分が勝利している | 300 |
|
| 3 | 「自 2 敵 0 空 1」が 2 つ以上存在する | 200 |
|
| 4 |
片方 の 斜め方向 に 〇×〇 が 並び、 いずれか の 辺 の 1 つのマスのみ に × が配置 されている |
100 |
|
| 5 |
「自 2 敵 0 空 1」が 1 つ存在する 「自 1 敵 0 空 2」が x 個存在する 「自 0 敵 1 空 2」が y 個存在する |
2 (0~2)0.5 * x (0~4)-y (-8~0) |
-8~6 |
| 2 |
「自 0 敵 2 空 1」が z 個存在する ただし、z > 0 とする |
-100 * z( -800 ~ -100) |
-800 ~ -100 |
ai13s の定義
ai12s を 上記の表 の 方法 で 評価値を計算 するように、修正 すると、これまで の ai12s ver 2 や 3 の 処理 を 行えなくなってしまう ので、新しく ai13s という 関数 を 下記 のように 定義 する事にします。また、上記 の $z$ に 乗算 する パラメータ を 実引数 で 変更できる ように、ai12s にあった 仮引数 score_defeat を そのまま利用 することにします。
- 10 行目:「自 0 敵 2 空 1」の マークのパターン が 存在する場合 の 評価値 を、上記 の 計算式 で 計算する ように 修正 する
1 from ai import ai_by_score
2 from marubatsu import Markpat
3 from pprint import pprint
4
5 def ai13s(mb, score_victory=300, score_sure_victory=200, score_defeat=-100,
6 score_special=100, score_201=2, score_102=0.5, score_012=-1, debug=False):
7 def eval_func(mb):
同じなので略
8 # 相手が勝利できる場合
9 if markpats[Markpat(last_turn=0, turn=2, empty=1)] > 0:
10 return score_defeat * markpats[Markpat(last_turn=0, turn=2, empty=1)]
同じなので略
行番号のないプログラム
from ai import ai_by_score
from marubatsu import Markpat
from pprint import pprint
def ai13s(mb, score_victory=300, score_sure_victory=200, score_defeat=-100,
score_special=100, score_201=2, score_102=0.5, score_012=-1, debug=False):
def eval_func(mb):
# 自分が勝利している場合
if mb.status == mb.last_turn:
return score_victory
markpats = mb.count_markpats()
if debug:
pprint(markpats)
# 相手が勝利できる場合
if markpats[Markpat(last_turn=0, turn=2, empty=1)] > 0:
return score_defeat * markpats[Markpat(last_turn=0, turn=2, empty=1)]
# 次の自分の手番で自分が必ず勝利できる場合
elif markpats[Markpat(last_turn=2, turn=0, empty=1)] >= 2:
return score_sure_victory
# 斜め方向に 〇×〇 が並び、いずれかの辺の 1 つのマスのみに × が配置されている場合
if mb.board[1][1] == Marubatsu.CROSS and \
(mb.board[0][0] == mb.board[2][2] == Marubatsu.CIRCLE or \
mb.board[2][0] == mb.board[0][2] == Marubatsu.CIRCLE) and \
(mb.board[1][0] == Marubatsu.CROSS or \
mb.board[0][1] == Marubatsu.CROSS or \
mb.board[2][1] == Marubatsu.CROSS or \
mb.board[1][2] == Marubatsu.CROSS) and \
mb.move_count == 4:
return score_special
# 評価値の合計を計算する変数を 0 で初期化する
score = 0
# 次の自分の手番で自分が勝利できる場合は評価値に score_201 を加算する
if markpats[Markpat(last_turn=2, turn=0, empty=1)] == 1:
score += score_201
# 「自 1 敵 0 空 2」1 つあたり score_102 だけ、評価値を加算する
score += markpats[Markpat(last_turn=1, turn=0, empty=2)] * score_102
# 「自 0 敵 1 空 2」1 つあたり score_201 だけ、評価値を減算する
score += markpats[Markpat(last_turn=0, turn=1, empty=2)] * score_012
# 計算した評価値を返す
return score
return ai_by_score(mb, eval_func, debug=debug)
修正箇所
from ai import ai_by_score
from marubatsu import Markpat
from pprint import pprint
-def ai13s(mb, score_victory=300, score_sure_victory=200, score_defeat=-100,
- score_special=100, score_201=2, score_102=0.5, score_012=-1, debug=False):
+def ai14s(mb, score_victory=300, score_sure_victory=200, score_defeat=-100,
+ score_special=100, score_201=2, score_102=0.5, score_012=-1, debug=False):
def eval_func(mb):
同じなので略
# 相手が勝利できる場合
if markpats[Markpat(last_turn=0, turn=2, empty=1)] > 0:
- return score_defeat
+ return score_defeat * markpats[Markpat(last_turn=0, turn=2, empty=1)]
同じなので略
ai13s が 5 手目で選択する合法手の確認

上図 の 局面 で、ai13s が 選択 する 合法手 を、下記 のプログラムで 確認します。
ai13s(mb, debug=True)
実行結果(長いのでクリックして開いてください)
Start ai_by_score
Turn x
x..
.ox
.Oo
legal_moves [(1, 0), (2, 0), (0, 1), (0, 2)]
====================
move (1, 0)
Turn o
xX.
.ox
.oo
defaultdict(<class 'int'>,
{Markpat(last_turn=0, turn=1, empty=2): 1,
Markpat(last_turn=0, turn=2, empty=1): 1,
Markpat(last_turn=1, turn=0, empty=2): 1,
Markpat(last_turn=1, turn=1, empty=1): 2,
Markpat(last_turn=1, turn=2, empty=0): 2,
Markpat(last_turn=2, turn=0, empty=1): 1})
score -100 best score -inf
UPDATE
best score -100
best moves [(1, 0)]
====================
move (2, 0)
Turn o
x.X
.ox
.oo
defaultdict(<class 'int'>,
{Markpat(last_turn=0, turn=2, empty=1): 2,
Markpat(last_turn=1, turn=0, empty=2): 1,
Markpat(last_turn=1, turn=1, empty=1): 2,
Markpat(last_turn=1, turn=2, empty=0): 1,
Markpat(last_turn=2, turn=0, empty=1): 1,
Markpat(last_turn=2, turn=1, empty=0): 1})
score -200 best score -100
====================
move (0, 1)
Turn o
x..
Xox
.oo
defaultdict(<class 'int'>,
{Markpat(last_turn=0, turn=1, empty=2): 1,
Markpat(last_turn=0, turn=2, empty=1): 2,
Markpat(last_turn=1, turn=0, empty=2): 1,
Markpat(last_turn=1, turn=1, empty=1): 1,
Markpat(last_turn=1, turn=2, empty=0): 1,
Markpat(last_turn=2, turn=0, empty=1): 1,
Markpat(last_turn=2, turn=1, empty=0): 1})
score -200 best score -100
====================
move (0, 2)
Turn o
x..
.ox
Xoo
defaultdict(<class 'int'>,
{Markpat(last_turn=0, turn=2, empty=1): 1,
Markpat(last_turn=1, turn=0, empty=2): 1,
Markpat(last_turn=1, turn=1, empty=1): 3,
Markpat(last_turn=1, turn=2, empty=0): 2,
Markpat(last_turn=2, turn=0, empty=1): 1})
score -100 best score -100
APPEND
best moves [(1, 0), (0, 2)]
====================
Finished
best score -100
best moves [(1, 0), (0, 2)]
下記は、先程の表 に、それぞれ の 合法手 の「自 0 敵 2 他 1」の マークのパターン の 数 と、上記 の 実行結果 に表示された 評価値 を 加えた ものです。
| 勝率 | 敗率 | 引分率 | 「021」 | 評価値 | ||
|---|---|---|---|---|---|---|
| 1 |  |
33 % | 33 % | 33 % | 1 | -100 |
| 2 |  |
33 % | 66 % | 0 % | 2 | -200 |
| 3 |  |
33 % | 66 % | 0 % | 2 | -200 |
| 4 |  |
33 % | 33 % | 33 % | 1 | -100 |
表 から、合法手 1、4 の (1, 0) と (0, 2) の 評価値 が 最も高い -100 になり、この 2 つ の 合法手のみ が 選択される ようになったことが 確認 できました。また、そのことは、下記の 実行結果 の 最後の 2 行 からも 確認 できます。
best score -100
best moves [(1, 0), (0, 2)]
上記から、ai13s が、ai12s ver 2 より も、上記の局面 で、相手によって は 成績 が 良くなる可能性 が 高くなる ような 合法手 を 選択するようになった ことが 確認 できました。
ai2 との対戦
下記 のプログラムで、ランダムな AI である ai2 と対戦 してみることにします。
from ai import ai_match, ai2
ai_match(ai=[ai13s, ai2])
実行結果(実行結果はランダムなので下記とは異なる場合があります)
ai13s VS ai2
count win lose draw
o 9888 0 112
x 8850 0 1150
total 18738 0 1262
ratio win lose draw
o 98.9% 0.0% 1.1%
x 88.5% 0.0% 11.5%
total 93.7% 0.0% 6.3%
実行結果 から、敗率 が 0 % であることが 確認 できたので、ai13s は 弱解決の AI である 可能性が高い ことが わかりました。
下記 は、上記 の 実行結果 に、ai12s ver 2 VS ai2 の 対戦結果 を 加えた ものです。実行結果 から、通算成績 はどちらも ほぼ同じ であることが分かりました。本当は ai13s VS ai2 のほう が 成績 が 良くなる ことを 期待していた のですが、そうはなりません でした。成績 が 変わらない原因 について少し考えてみて下さい。
| 関数名 | o 勝 | o 負 | o 分 | x 勝 | x 負 | x 分 | 勝 | 負 | 分 |
|---|---|---|---|---|---|---|---|---|---|
ai12s ver 2 |
98.9 | 0.0 | 1.1 | 88.7 | 0.0 | 11.3 | 93.8 | 0.0 | 6.2 |
ai13s |
98.9 | 0.0 | 1.1 | 88.5 | 0.0 | 11.5 | 93.7 | 0.0 | 6.3 |
ai12s ver 2 VS ai2 と ai13s VS ai2 の違いの検証

先程、上記の局面 で、ai12s ver 2 と ai13s が 選択 する 合法手 が 異なる ことを 確認 しました。それにもかかわらず、上記の表のように 成績 が 変わらない ということは、ai12s ver 2 VS ai2 と ai13s VS ai2 の 対戦 で、上記のような、ai12s ver 2 と ai13s で 異なる合法手 を 選択する局面 が 出現しない ことが 原因 である 可能性 が あります。
そこで、ai12s ver 2 VS ai2 と ai13s VS ai2 の 結果 の 差が生じる ような 試合 が 存在するか どうかを、前回の記事と 同様の方法 で、下記 のプログラムで 検証する ことにします。ただし、前回の記事 の プログラム では 結果 に 差が生じるまで、無限ループ で 処理 を 行いました が、差が生じる ような 局面 が 存在しない 場合は プログラム が 終了しない ので、1 万回繰り返し ても 見つからない 場合は、処理を終了する ように 修正 しました。
- 7 行目:無限ループ を、10000 回繰り返す ように 修正 する
-
9、12 行目:
ai12ver 3 VSai2をai13VSai2に 修正 する
1 import random
2 from marubatsu import Marubatsu
3 from ai import ai2, ai12s
4
5 seed = 0
6 mb = Marubatsu()
7 while seed < 10000:
8 winner1 = mb.play(ai=[ai12s, ai2], seed=seed, verbose=False)
9 winner2 = mb.play(ai=[ai13s, ai2], seed=seed, verbose=False)
10 if winner1 != winner2:
11 mb.play(ai=[ai12s, ai2], seed=seed)
12 mb.play(ai=[ai13s, ai2], seed=seed)
13 break
14 seed += 1
行番号のないプログラム
import random
from marubatsu import Marubatsu
from ai import ai2, ai12s
seed = 0
mb = Marubatsu()
while seed < 10000:
winner1 = mb.play(ai=[ai12s, ai2], seed=seed, verbose=False)
winner2 = mb.play(ai=[ai13s, ai2], seed=seed, verbose=False)
if winner1 != winner2:
mb.play(ai=[ai12s, ai2], seed=seed)
mb.play(ai=[ai13s, ai2], seed=seed)
break
seed += 1
修正箇所
import random
from marubatsu import Marubatsu
from ai import ai2, ai12s
seed = 0
mb = Marubatsu()
-while True:
+while seed < 10000:
winner1 = mb.play(ai=[ai12s, ai2], seed=seed, verbose=False)
- winner2 = mb.play(ai=[ai12s, ai2], params=[{"score_victory": 200}, {}], \
- seed=seed, verbose=False)
+ winner2 = mb.play(ai=[ai13s, ai2], seed=seed, verbose=False)
if winner1 != winner2:
mb.play(ai=[ai12s, ai2], seed=seed)
- mb.play(ai=[ai12s, ai2], params=[{"score_victory": 200}, {}], seed=seed)
+ mb.play(ai=[ai13s, ai2], seed=seed)
break
seed += 1
実行結果
実行結果 には 何も表示されない ので、想像した通りに、差が生じる ような 局面 が 出現しない ことが わかりました。
なお、ゲーム開始時 の 局面 から ai13s VS ai2 の 対戦 を行った場合は、確かに 差が生じる ような 局面 は 出現しません が、例えば 最初 は 人間が着手 を行い、途中から ai13s が 着手を行う ような場合は、差が生じる局面 は 下図 のように 実際に出現 します。従って、ai13s を 作成したこと が、無意味 であるというわけでは ありません。

他の優先順位の条件を考慮に入れた、必敗の局面での最善手の評価値の計算
ルール 13 では、必敗の局面 での 評価値 を 計算する際 に、「自 0 敵 2 空 1」の マークのパターン の 数のみ を 考慮 入れた 式 で 評価値 を 計算 しました。
必敗の局面 の 合法手 の 優劣を決める 際に、必敗の局面以外 の場合で 有効であった、他の優先順位 の ヒューリスティックな条件 の 評価値 が 有効 である 可能性 が あります。
ルール 14 の定義
そこで、必敗の局面 の 評価値 に ヒューリスティックな条件 の 評価値 を 組み込む という ルール 14 を下記のように 定義 することにします。具体的には、ルール 13 の 優先順位 が 2 の 条件 に『また、優先順位 が 5 の条件 も 考慮 する』を 加えました。
| 順位 | 条件 | 種類 |
|---|---|---|
| 1 | 勝てる場合 に 勝つ | 十分条件 |
| 2 |
相手 が 勝利できる 着手を 行わない ただし、「自 0 敵 2 空 1」の 数 が 少ない着手 を 優先 する また、優先順位 が 5 の条件 も 考慮 する |
必要条件 |
| 3 | 「自 2 敵 0 空 1」が 2 つ以上存在 する着手を行う | 十分条件 |
| 4 |
斜め方向 に 〇×〇 が 並び、他の 6 マス が 空のマス の 場合は、いずれか の 辺のマス に着手を行う |
十分条件 |
| 5 | 「自 2 敵 0 空 1」が 1 つ存在 する着手を行う 「自 1 敵 0 空 2」が 最も多い 着手を行う 「自 0 敵 1 空 2」が 最も少ない 着手を行う |
|
| 6 | ランダム なマスに 着手 する |
評価値の設定
次に、ルール 14 の、優先順位が 2 の 条件 の 評価値 を 計算する方法 を 考える必要 があります。その方法として、下記 のような 方法 が 考えられます。
- ルール 13 の 優先順位が 5 の 条件 の 評価値 に、優先順位が 5 の ヒューリスティックな条件 の 評価値 を 加算 する
その際に、先程と同様 に、計算 された 評価値 の 範囲 が、他 の 優先順位 の 条件 の 評価値 の 範囲 と 重ならない ようにする 必要 があります。
下記は、そのこと を 確認 するために、それぞれ の 優先順位 の 条件 に対する 評価値 の 範囲 を まとめた表 です。表 から、それぞれ の 優先順位 で 計算 される 評価値 の 範囲 が 重複していない ことが 確認 できます。
| 順位 | 局面の状況 | 個別 | 評価値 |
|---|---|---|---|
| 1 | 自分が勝利している | 300 |
|
| 3 | 「自 2 敵 0 空 1」が 2 つ以上存在する | 200 |
|
| 4 |
片方 の 斜め方向 に 〇×〇 が 並び、 いずれか の 辺 の 1 つのマスのみ に × が配置 されている |
100 |
|
| 5 |
「自 2 敵 0 空 1」が 1 つ存在する 「自 1 敵 0 空 2」が x 個存在する 「自 0 敵 1 空 2」が y 個存在する |
2 (0~2)0.5 * x (0~4)-y (-8~0) |
-8~6 |
| 2 |
「自 0 敵 2 空 1」が z 個存在する ただし、z > 0 とし、優先順位 が 5 の 評価値 を 加算 する |
-100 * z( -800 ~ -100)+ -8~6
|
-808 ~ -94 |
評価値を加算する際の注意点
上記では、優先順位 が 2 の 評価値 の 範囲 が、その上の 優先順位 が 5 の 評価値 の 範囲 と 重ならない ことを 確認 しましたが、それだけ では 意図通り の 評価値 が 計算されない 場合が ある 点に 注意 が 必要 です。
例えば、ai13s では、「自 0 敵 2 空 1」の マークのパターン の 数 が 少ない合法手 を 優先的 に 選択 するようにするために、「自 0 敵 2 空 1」の マークのパターン の 数 が 1 つあたり の 評価値 を -100 に 設定 しました。
ルール 14 の 評価値 を 設定 する 際 に、この『「自 0 敵 2 空 1」の マークのパターン の 数 が 少ない合法手 を 優先的 に 選択する』という 条件 が、ヒューリスティックな条件 よりも 重要である と 考える のであれば、ヒューリスティックな条件 による 評価値 を 加算 しても、「自 0 敵 2 空 1」の マークのパターン の 数 が 少ない場合 の 評価値 が 大きくなるよう に、評価値 を 設定 する 必要 が あります。そのことを 確認したほう が 良い でしょう。
下記 は、「自 0 敵 2 空 1」の マークのパターン の 1 つあたり の 評価値 を -100 とした場合に、「自 0 敵 2 空 1」の マークのパターン の 数 が 1 ~ 3 の 場合 のそれぞれの 評価値 の 範囲 を 表す表 です。表から、この場合は、「自 0 敵 2 空 1」の マークのパターン の それぞれの数 に対する 評価値の範囲 が、重ならない ので、 マークのパターン の 数 が 少ない場合 の 評価値 が 必ず大きくなる ことが 確認 できます。
そこで、本記事では、「自 0 敵 2 空 1」の マークのパターン の 数 が 1 つあたり の 評価値 を ai13s と同様 に、-100 に 設定 することにします。
| 局面の状況 | 個別 | 評価値 |
|---|---|---|
|
「自 2 敵 0 空 1」が 1 つ存在する 「自 1 敵 0 空 2」が x 個存在する 「自 0 敵 1 空 2」が y 個存在する |
2 (0~2)0.5 * x (0~4)-y (-8~0) |
-8~6 |
| 「自 0 敵 2 空 1」が 1 個存在する |
-100+ -8~6
|
-108 ~ -94 |
| 「自 0 敵 2 空 1」が 2 個存在する |
-200+ -8~6
|
-208 ~ -194 |
| 「自 0 敵 2 空 1」が 3 個存在する |
-300+ -8~6
|
-308 ~ -294 |
下記は、「自 0 敵 2 空 1」の 1 つあたり の 評価値 を -10 に 設定 した場合の 表 です。表から、この場合は、「自 0 敵 2 空 1」の それぞれ の マークのパターン の 数 に対する 評価値 の 範囲 が、他の数 に対する 評価値 の 範囲 の 一部 に 重なっている(例えば -18 ~ -14 が 重なっている)ことが わかる ので、目的 を 達成できません。
| 局面の状況 | 個別 | 評価値 |
|---|---|---|
|
「自 2 敵 0 空 1」が 1 つ存在する 「自 1 敵 0 空 2」が x 個存在する 「自 0 敵 1 空 2」が y 個存在する |
2 (0~2)0.5 * x (0~4)-y (-8~0) |
-8~6 |
| 「自 0 敵 2 空 1」が 1 個存在する | -10 + -8~6
|
-18 ~ -4 |
| 「自 0 敵 2 空 1」が 2 個存在する | -20 + -8~6
|
-28 ~ -14 |
| 「自 0 敵 2 空 1」が 3 個存在する | -30 + -8~6
|
-38 ~ -24 |
このように、異なる優先順位 の 評価値 を 合計 する場合は、上記のような 表を作成 して、意図通り の 評価値が設定 されているかどうかを 確認 することが 重要 です。
逆に、「自 0 敵 2 空 1」の マークのパターン の 数より も、ヒューリスティックな条件 のほうが 重要である と 考える のであれば、上記 の 設定 で 問題 は ありません。
ai14s の定義
下記は、上記 の 評価値 の 計算 を行う ai14s を 定義 するプログラムです。
-
5、10 行目:評価値 の 合計 を 計算 する変数
scoreの 初期化処理 を、eval_funcの 最初で行う ように 修正 する -
8 行目:相手が勝利 できる 場合 に、これまで は 計算した 評価値 を return 文 で 返していた のを、
scoreに 加算する ように 修正 する。そのようにすることで、scoreに 12 行目以降 の ヒューリスティックな条件に よって 計算 された 評価値 が 加算される
1 def ai14s(mb, score_victory=300, score_sure_victory=200, score_defeat=-100,
2 score_special=100, score_201=2, score_102=0.5, score_012=-1, debug=False):
3 def eval_func(mb):
4 # 評価値の合計を計算する変数を 0 で初期化する
5 score = 0
同じなので略
6 # 相手が勝利できる場合は評価値を加算する
7 if markpats[Markpat(last_turn=0, turn=2, empty=1)] > 0:
8 score = score_defeat * markpats[Markpat(last_turn=0, turn=2, empty=1)]
同じなので略
9 # この下にあった評価値の合計を計算する変数を 0 で初期化する処理を削除する
10
11 # 次の自分の手番で自分が勝利できる場合は評価値に score_201 を加算する
12 if markpats[Markpat(last_turn=2, turn=0, empty=1)] == 1:
同じなので略
行番号のないプログラム
def ai14s(mb, score_victory=300, score_sure_victory=200, score_defeat=-100,
score_special=100, score_201=2, score_102=0.5, score_012=-1, debug=False):
def eval_func(mb):
# 評価値の合計を計算する変数を 0 で初期化する
score = 0
# 自分が勝利している場合
if mb.status == mb.last_turn:
return score_victory
markpats = mb.count_markpats()
if debug:
pprint(markpats)
# 相手が勝利できる場合は評価値を加算する
if markpats[Markpat(last_turn=0, turn=2, empty=1)] > 0:
score = score_defeat * markpats[Markpat(last_turn=0, turn=2, empty=1)]
# 次の自分の手番で自分が必ず勝利できる場合
elif markpats[Markpat(last_turn=2, turn=0, empty=1)] >= 2:
return score_sure_victory
# 斜め方向に 〇×〇 が並び、いずれかの辺の 1 つのマスのみに × が配置されている場合
if mb.board[1][1] == Marubatsu.CROSS and \
(mb.board[0][0] == mb.board[2][2] == Marubatsu.CIRCLE or \
mb.board[2][0] == mb.board[0][2] == Marubatsu.CIRCLE) and \
(mb.board[1][0] == Marubatsu.CROSS or \
mb.board[0][1] == Marubatsu.CROSS or \
mb.board[2][1] == Marubatsu.CROSS or \
mb.board[1][2] == Marubatsu.CROSS) and \
mb.move_count == 4:
return score_special
# 次の自分の手番で自分が勝利できる場合は評価値に score_201 を加算する
if markpats[Markpat(last_turn=2, turn=0, empty=1)] == 1:
score += score_201
# 「自 1 敵 0 空 2」1 つあたり score_102 だけ、評価値を加算する
score += markpats[Markpat(last_turn=1, turn=0, empty=2)] * score_102
# 「自 0 敵 1 空 2」1 つあたり score_201 だけ、評価値を減算する
score += markpats[Markpat(last_turn=0, turn=1, empty=2)] * score_012
# 計算した評価値を返す
return score
return ai_by_score(mb, eval_func, debug=debug)
修正箇所
-def ai13s(mb, score_victory=300, score_sure_victory=200, score_defeat=-100,
- score_special=100, score_201=2, score_102=0.5, score_012=-1, debug=False):
+def ai14s(mb, score_victory=300, score_sure_victory=200, score_defeat=-100,
+ score_special=100, score_201=2, score_102=0.5, score_012=-1, debug=False):
def eval_func(mb):
+ # 評価値の合計を計算する変数を 0 で初期化する
+ score = 0
同じなので略
# 相手が勝利できる場合は評価値を加算する
if markpats[Markpat(last_turn=0, turn=2, empty=1)] > 0:
- return score_defeat * markpats[Markpat(last_turn=0, turn=2, empty=1)]
+ score += score_defeat * markpats[Markpat(last_turn=0, turn=2, empty=1)]
同じなので略
# 評価値の合計を計算する変数を 0 で初期化する
- score = 0
# 次の自分の手番で自分が勝利できる場合は評価値に score_201 を加算する
if markpats[Markpat(last_turn=2, turn=0, empty=1)] == 1:
同じなので略
ai14s が 5 手目で選択する合法手の確認

上図 の 局面 で、ai14s が 選択 する 合法手 を、下記 のプログラムで 確認 します。
ai14s(mb, debug=True)
実行結果(長いのでクリックして開いてください)
Start ai_by_score
Turn x
x..
.ox
.Oo
legal_moves [(1, 0), (2, 0), (0, 1), (0, 2)]
====================
move (1, 0)
Turn o
xX.
.ox
.oo
defaultdict(<class 'int'>,
{Markpat(last_turn=0, turn=1, empty=2): 1,
Markpat(last_turn=0, turn=2, empty=1): 1,
Markpat(last_turn=1, turn=0, empty=2): 1,
Markpat(last_turn=1, turn=1, empty=1): 2,
Markpat(last_turn=1, turn=2, empty=0): 2,
Markpat(last_turn=2, turn=0, empty=1): 1})
score -98.5 best score -inf
UPDATE
best score -98.5
best moves [(1, 0)]
====================
move (2, 0)
Turn o
x.X
.ox
.oo
defaultdict(<class 'int'>,
{Markpat(last_turn=0, turn=2, empty=1): 2,
Markpat(last_turn=1, turn=0, empty=2): 1,
Markpat(last_turn=1, turn=1, empty=1): 2,
Markpat(last_turn=1, turn=2, empty=0): 1,
Markpat(last_turn=2, turn=0, empty=1): 1,
Markpat(last_turn=2, turn=1, empty=0): 1})
score -197.5 best score -98.5
====================
move (0, 1)
Turn o
x..
Xox
.oo
defaultdict(<class 'int'>,
{Markpat(last_turn=0, turn=1, empty=2): 1,
Markpat(last_turn=0, turn=2, empty=1): 2,
Markpat(last_turn=1, turn=0, empty=2): 1,
Markpat(last_turn=1, turn=1, empty=1): 1,
Markpat(last_turn=1, turn=2, empty=0): 1,
Markpat(last_turn=2, turn=0, empty=1): 1,
Markpat(last_turn=2, turn=1, empty=0): 1})
score -198.5 best score -98.5
====================
move (0, 2)
Turn o
x..
.ox
Xoo
defaultdict(<class 'int'>,
{Markpat(last_turn=0, turn=2, empty=1): 1,
Markpat(last_turn=1, turn=0, empty=2): 1,
Markpat(last_turn=1, turn=1, empty=1): 3,
Markpat(last_turn=1, turn=2, empty=0): 2,
Markpat(last_turn=2, turn=0, empty=1): 1})
score -97.5 best score -98.5
UPDATE
best score -97.5
best moves [(0, 2)]
====================
Finished
best score -97.5
best moves [(0, 2)]
下記は、先程の表 から 勝率など を 削除 し、評価値 の 計算 で 利用 する マークのパターン の 数 と、上記 の 実行結果 に表示された 評価値 を 加えた ものです。
| 「201」 | 「021」 | 「102」 | 「012」 | 評価値 | ||
|---|---|---|---|---|---|---|
| 評価値 | 1:+22~: 200
|
1 つで-100
|
1 つで+0.5
|
1 つで-1
|
||
| 1 |  |
1 | 1 | 1 | 1 | -98.5 |
| 2 |  |
1 | 2 | 1 | -197.5 | |
| 3 |  |
1 | 2 | 1 | 1 | -198.5 |
| 4 |  |
1 | 1 | 1 | -97.5 |
表から、合法手 4 の (0, 2) の 評価値 が 最も高い -97.5 になり、この合法手のみ が 選択 されるようになったことが 確認 できました。また、そのことは、下記の 実行結果 の 最後の 2 行 からも 確認 できます。
best score -97.5
best moves [(0, 2)]
なお、ai13s と ai14s は、上記のように 同じ局面 で 異なる合法手 を 選択する ようになりましたが、どちら が 強い AI であるか を、ランダムな AI と 対戦 して 判定 することは できません。その理由 は、先程説明したように、この局面 は、ランダムな AI と 対戦 した際に 生じない局面 だからです。ai13s と ai14s の どちら が 最強の AI に近い かどうかについては、探索型の AI を 作成する際 に 確認する ことにします。
ai2 との対戦
下記 のプログラムで、ランダムな AI である ai2 と対戦 してみることにします。
ai_match(ai=[ai14s, ai2])
実行結果(実行結果はランダムなので下記とは異なる場合があります)
ai14s VS ai2
count win lose draw
o 9900 0 100
x 8885 0 1115
total 18785 0 1215
ratio win lose draw
o 99.0% 0.0% 1.0%
x 88.8% 0.0% 11.2%
total 93.9% 0.0% 6.1%
実行結果 から、敗率 が 0 % であることが 確認 できたので、ai14s は 弱解決の AI である 可能性が高い ことが わかりました。
下記は、上記 の 実行結果 に、ai12s ver 2 VS ai2 と ai13s VS ai2 の 対戦結果 を 加えた ものです。実行結果 から、通算成績 は いずれもほぼ同じ であることが わかりました。
なお、通算成績 が 変わらない理由 は、ai13s と ai14s の 違い が、ai13s VS ai2 や ai14s VS ai2 で 出現しない局面 に対する 評価値 の 計算 だからです。
| 関数名 | o 勝 | o 負 | o 分 | x 勝 | x 負 | x 分 | 勝 | 負 | 分 |
|---|---|---|---|---|---|---|---|---|---|
ai12s ver 2 |
98.9 | 0.0 | 1.1 | 88.7 | 0.0 | 11.3 | 93.8 | 0.0 | 6.2 |
ai13s |
98.9 | 0.0 | 1.1 | 88.5 | 0.0 | 11.5 | 93.7 | 0.0 | 6.3 |
ai14s |
99.0 | 0.0 | 1.0 | 88.8 | 0.0 | 11.2 | 93.9 | 0.0 | 6.1 |
今回の記事のまとめ
今回の記事では、最初に ai12s ver 3 の バグの原因 を 検証 しました。このように、ルールベースの AI では、正しい と 思っていた条件 が 正しくなかった ということが あります。
次に、必勝の局面 と、必敗の局面 での、最善手の優劣 について 説明 しました。いずれの場合 も、相手 が 最強の AI の 場合 は 最善手 に 優劣 は ありません が、最強ではない AI や 人間 と 対戦 する場合を 考慮に入れる と、最善手 の間に 優劣が生じる 場合が あります。
特に 人間と対戦 を行うことを 想定する 場合は、必勝の局面 の場合では 人間の心理 を 考慮に入れた優劣 を 評価値の計算 に 組み込んだほうが良い でしょう。
また、必敗の局面 でも、評価値 の 計算 を 工夫 することによって、相手 が 最強の AI でない 場合に、より良い結果 になる 確率が高い 最善手を 選択できる ようになることを説明しました。ただし、その際に、計算される 評価値の範囲 に 注意 する 必要がある ことを 忘れないで下さい。
なお、今回の記事では説明を省略しましたが、引き分けの局面 の 最善手 にも、同様の意味 での 優劣 が 存在します。
ルールベースの AI について、〇×ゲーム で 思いつく範囲 の 説明 は ほぼ行った のではないかと思いますので、ルールベースの AI に関する 説明 は 今回の記事 で 終わり にします。ただし、ルールベースの AI に関する 重要な内容 を 思いついた場合 は、適宜説明 します。
本記事では、マークのパターン を 利用 した ルール の 条件 を作成してきましたが、局面の状況 を うまく表す他の性質 を考え、その性質を使って 条件 を 考える ことも できます。興味や時間がある方は考えてみると良いでしょう。
ここまでの記事を読んで、ルールベース で AI を作成 することが、非常に大変 であることが 実感できた のではないかと 思います。また、〇×ゲーム は、単純なゲーム なので、ルールベースの AI でも、弱解決の AI を 作成 することが できました が、〇×ゲームより も 複雑なゲーム の ほとんど は、ルールベースの AI で 弱解決の AI を 作成 することは 非常に困難 か、ほぼ不可能 です。そのため、これまでに何度か言及してきましたが、最近 では ルールベース で ゲームの AI を 作成 することは 主流 では なくなっています。
それにもかかわらず、本記事 が 最初 に、主流ではない、ルールベース で AI を作成 してきた 主な理由 は、以下の通り です。
- ルールベース の AI の 考え方 が、人間 が 問題 を 解決 するための 考え方 に 似ている
- 昔 は、ルールベース の AI が 主流 であった
- 〇×ゲーム であれば、ルールベース で 弱解決の AI を 作成できる
- ルール を 少しづつ加えていく ことで、AI を 作り上げていく ことが できる
- 初心者 が プログラミング の 基礎 を 学ぶため の 重要な題材 が 豊富 である
次回からは、〇×ゲームの AI に関する別の内容を説明したいと思います。
本記事で入力したプログラム
以下のリンクから、本記事で入力して実行した JupyterLab のファイルを見ることができます。
今回の記事では marubatsu.py は変更していません。
以下のリンクは、今回の記事で更新した ai.py です。
次回の記事